电液伺服系统多模型鲁棒自适应控制
2018-11-14成旭华姚建勇乐贵高
成旭华,姚建勇,乐贵高
(南京理工大学机械工程学院,290014,南京)
电液伺服系统具有动态响应快、体积小、输出力/转矩大及控制精确度高等突出优点,在国防、航空航天、民用等领域得到了广泛应用。电液伺服系统是一个典型的非线性系统,包括各种非线性特性和建模不确定性,如摩擦非线性、电液伺服阀流量压力非线性等非线性特性,电液伺服阀流量增益、泄漏系数、负载质量、执行机构的黏性摩擦系数、液压油弹性模量等未知参数以及外部干扰、未建模动态、死区等建模不确定性[1-2],这些非线性限制了电液伺服系统高性能控制器的发展。为了提高非线性系统的控制性能,越来越多的研究人员设计了各种非线性控制器[3-6],滑模[7]、自适应[8]、自适应鲁棒[9-10]等方法相继运用到液压非线性运动控制中。
液压系统中部分参数的不确定性比较大,如液压油弹性模量可从100 MPa到1 400 MPa,泄漏系数可从1×10-13m5/(N·s)到1×10-10m5/(N·s)等。传统自适应控制对参数自适应初值比较敏感,系统存在强参数不确定性时,初值的选取将影响系统的瞬态响应性能,甚至闭环稳定性。针对此类问题,多模自适应控制被提出,且受到广泛关注。文献[11]针对线性系统建立含有多个固定模型和两个自适应模型,提出一种有停留时间的切换策略,并分析了系统的稳定性。李晓理等设计了一种基于有界扰动分区的多模型自适应控制,解决了含有界扰动的离散时间系统输出跟踪问题,提高了系统控制性能[12]。邵彭真等设计了一种多模型切换自适应控制器,解决了轧机电液伺服系统在空载和负载两种不同工况的切换控制。针对线性系统,Han等提出一种二阶多模型自适应控制[14],运用凸集的概念,减小了辨识模型的个数,且具有一定的鲁棒性能[15]。随后,陈杰等提出非线性系统的二阶多模型自适应控制[16-17],但没有考虑存在外部干扰等不确定性的情况。自适应控制在存在外部干扰、未建模动态等不确定性时,系统跟踪性能将会受到影响。
本文针对电液伺服系统的特点,建立了系统的数学模型以及多个辨识模型,在辨识模型中设计非线性鲁棒项,以减小外部干扰等不确定性的影响,并基于反步法和李雅普诺夫分析法设计了一种考虑强参数不确定性和不确定非线性的多模型鲁棒自适应控制器(MMRAC),使系统得到了渐进跟踪的性能,提高了系统的瞬态响应性能。实验结果证明了所设计控制器的有效性。
1 系统建模与问题描述
本文所研究的电液伺服系统如图1所示,图中右侧的负载被伺服液压缸驱动。控制器设计的目标是在电液伺服系统的输出下使得负载位移尽可能地跟踪任意指定的位移轨迹。电液伺服系统的动力学方程可以表示为
(1)


图1 电液伺服系统示意图
忽略伺服液压缸的外泄漏,则伺服液压缸的压力动态方程为[1]
(2)
式中:Vt为伺服液压缸的总容积;βe为有效油液弹性模量;Ct为内泄漏系数;QL为负载流量;q(t)为建模误差。
采用高响应的电液伺服阀,则阀芯位移xv与控制输入u近似为比例环节,即xv=kiu,因此得到电液伺服阀流量方程
(3)


(4)

(5)
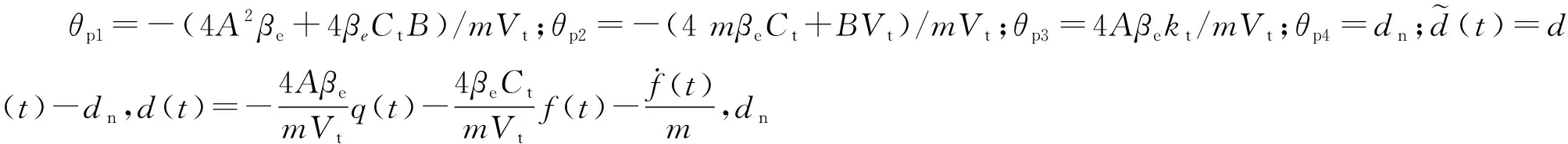
对于确定的液压系统,有以下合理的假设。
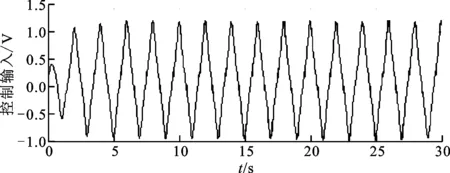
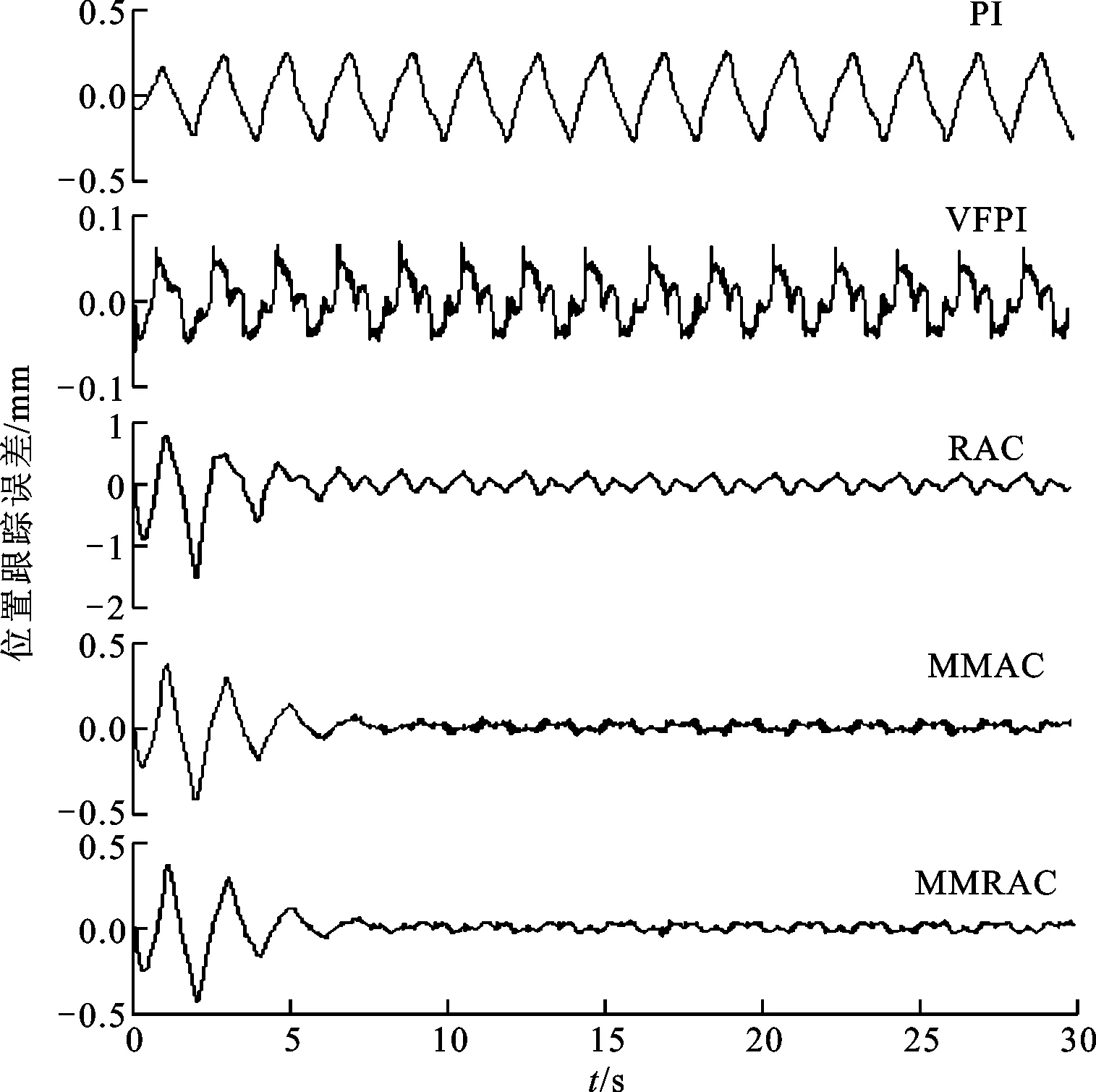
假设1系统的指令信号yd(t)=x1d(t)∈C3且有界;实际液压系统在一般工况下满足0 假设2系统参数不确定性θ的范围已知,即 θp∈Ωpθ{θp:θpmin≤θp≤θpmax} (6) 式中:θpmin=[θp1min,θp2min,θp3min,θp4min]T、θpmax=[θp1max,θp2max,θp3max,θp4max]T是向量θp已知的上下界,θp3min>0。 (7) 在控制器设计分析过程中,将用到以下引理。 引理1∀x∈R,a>0,有 0≤xtanh(x/a)≤|x| (8) 引理2∀x≥0,y>0或x>0,y≥0有 x/x+y≤1 (9) 对系统进行在线辨识,根据系统状态方程(5)设计多个辨识模型如下 (10) 如上所示,各辨识模型的形式是一样的,只是参数估计的初值不同。 (11) 式中:j=1,2,3,4表示为第几个参数;τij为参数自适应函数,在后续控制器设计中决定其具体形式。 给定如下参数自适应率 (12) 式中Γ>0为正定对角矩阵。 对于任意的参数自适应函数τi,不连续映射式(12)满足以下性质 P1θi∈Ωθi{θi:θpmin≤θi≤θpmax} (13) (14) 基于各个辨识模型,用反步设计方法设计相应的控制器ui。 定义emi1=xi1-x1d,则 (15) 令αi1为xi2的虚拟控制输入,定义αi1与xi2的误差为emi2=xi2-αi1,则 (16) 设计虚拟控制输入 (17) 式中k1>0为可调增益。 将式(17)代入式(16)得 (18) 令αi2为xi3的虚拟控制输入,定义αi2与xi3的误差为emi3=xi3-αi2,则 (19) 设计虚拟控制输入 (20) 式中k2>0为可调增益。 将式(20)代入式(19)得 (21) 对emi3求导,得到其动态方程如下 (22) 基于式(22)设计控制器 ui=uia+uis (23) 式中k3>0为可调增益。 将控制器式(23)代入式(22)得 (24) 对系统进行在线辨识并基于辨识模型设计控制器,其动机是通过辨识模型的稳定使得被控对象稳定。因此,如果使用多个辨识模型,具有最佳性能的模型也将产生最佳的控制性能。为了提高系统控制性能,需要在任何时刻有可靠的辨识性能指标。本文采用的切换方案是对基于系统辨识误差的指标函数进行监视,每次切换时选择对应于指标函数值最小的辨识模型的控制器作为系统的当前控制输入。 本文选择的性能指标函数为 (25) 式中:α>0、β>0为对应项的权重,分别决定实时和历史辨识误差在性能指标中的权重。 切换函数 S(t)=sub(Ji(t)=Jmin(t),i=1,2,…,N) u=us(t) (26) 式中:sub(·)为取下标函数;Jmin(t)为t时刻各个辨识模型的性能指标函数中的最小值。将基于性能指标函数最小的辨识模型设计的控制器切换为当前控制器,即u=us(t),且切换间隙Tmin>ε,ε为任意小的数,以防止无限切换。 定义系统真实位移和系统给定指令的误差z=xp1-x1d。 定理对于电液伺服系统式(5),取参数自适应函数 τi=φei3 (27) 式中:φ=[-xp2,-xp3,-gu,-1]T。 取M的自适应率 (28) 式中γ>0为参数自适应增益。 选取λ1,λ2,λ3,k1,k2,k3使得如下定义的矩阵为正定矩阵 则控制器式(23)及切换函数式(26)保证闭环系统中所有信号均有界,可获得渐近稳定跟踪,即当t→∞时,z→0,并且提高了系统的瞬态响应性能。 证明假设某一时刻控制器为ui,取李雅普诺夫函数为 (29) 对其求导得 (30) 将参数自适应率式(11)(28)代入式(30)得 (31) 式中Ei=[emi1,emi2,emi3ei1,ei2,ei3]T。 (32) 对式(32)两边进行积分,得 (33) z=xp1-x1d=(xi1-x1d)- (xi1-xp1)=emi1-ei1 (34) 由上述证明过程可知,每一个控制器都可以使系统稳定。因此,控制器式(23)和切换函数式(26)可以使得系统任意时刻都是稳定的,即t→∞时,z→0,且把离真实系统最近的辨识模型所设计的控制器切换为系统当前控制器,提高了系统的瞬态响应性能。 建立如图2所示的阀控电液位置伺服系统,其系统参数与文献[3]相同。系统的供油压力Ps=10 MPa,Pr=0.08 MPa,采样时间为0.5 ms。 图2 电液位置伺服系统实验平台 对比以下5种控制器以验证所提出控制器的有效性。 (1)MMRAC。本文所提出的多模型鲁棒自适应控制器,控制器参数k1=1 000,k2=200,k3=50,λ1=1 000,λ2=400,λ3=100,γ=0.05,Γ=diag[20 000,0.2,1×10-5,50]。建立了4个辨识模型,θ1(0)=[-1×105,-100,15,0]T,θ2(0)=[-5×105,-500,30,0]T,θ3(0)=[-1×106,-1 000,50,0]T,θ4(0)=[-2×106,-2 000,90,0]T,Mi(0)=10,δ(t)=10 000/(t2+1)。取α=1,β=1,初始控制器选为u2。 (2)鲁棒自适应控制器(RAC)。传统的RAC,参数自适应初值θ(0)=[-5×105,-500,30,0]T,其余参数同MMRAC。 (3)多模型自适应控制器(MMAC)。与MMRAC的区别在于辨识模型中没有非线性鲁棒项,控制器参数同MMRAC。 (4)PI控制器。控制器参数kp=8 000,ki=2 000。 (5)VFPI控制器。该控制器是速度前馈PI控制器,速度增益kv选为0.028 1 V·s/mm,这种控制结构在工业中被广泛使用,其增益与PI控制器相同。 采用最大跟踪误差Me、平均跟踪误差μ、跟踪误差的标准差σ等指标[6]来评估以上5种控制器的性能。 为验证所提出算法的有效性,选取两种不同工况进行实验验证。 工况1:取系统指令x1d=10arctan(sin(πt))·[1-e-t]/0.785 4 (mm),该指令保证了假设1的条件。MMRAC作用下系统位置跟踪、控制器输入、伺服液压缸两腔的压力值、切换函数分别如图3~图6所示,5种控制器作用下系统位置跟踪误差如图7所示。5种控制器作用下最后两周期的性能指标如表1所示。 图3 MMRAC作用下系统的位置跟踪 图4 MMRAC的控制输入 图5 伺服液压缸两腔的压力值 图6 MMRAC控制器切换图 由位置跟踪误差图7及表1中后两周期的性能指标可以看出,MMRAC的各项性能指标均最优。由于RAC参数自适应初值选取得不合适,导致其跟踪性能较差,而MMRAC采用了多个辨识模型,其瞬态响应较RAC有了明显的提高。与MMAC相比,MMRAC通过在辨识模型中加入非线性鲁棒项,抑制了外部干扰、未建模动态等不确定性的影响,提高了系统辨识的精度。由于MMRAC基于更为准确的辨识模型设计相应控制器,从而提高了系统的控制性能。从图6可以看出,MMRAC的初始控制输入为u2,在经过一个采样周期后,系统的控制输入切换到u1,而后面S(t)的值不再变化,说明已经切换到最佳的控制器。PI控制器对模型不确定性有一些鲁棒性,其跟踪误差比其他4种控制器都要差。VFPI控制器中加入了速度前馈,利用速度前馈消除主要的模型动态,同时通过大的反馈增益抑制其他未考虑的因素,但其性能指标仍不如MMRAC。 图7 工况1下各控制器位置跟踪误差比较图 控制器MeμσPI0.265 10.136 60.079 1VFPI0.062 50.021 20.013 3RAC0.195 30.071 60.046 9MMAC0.054 90.018 50.011 6MMRAC0.038 60.017 90.007 6 工况2:为了进一步验证算法的有效性,选取系统指令x1d=30arctan(sin(0.4πt))[1-e-t]/0.785 4 (mm)。5种控制器的位置跟踪误差如图8所示,最后两周期的性能指标如表2所示。 同样,从实验结果可以看出,MMRAC的各项性能指标均优于其他4种控制器,从而进一步验证了所提出算法的有效性。 图8 工况2下各控制器位置跟踪误差比较图 控制器MeμσPI0.230 30.134 10.062 1VFPI0.055 10.016 00.012 2RAC0.190 90.069 60.042 1MMAC0.045 70.008 50.007 1MMRAC0.032 90.007 80.005 7 本文针对电液伺服系统存在的强参数不确定性和不确定非线性,设计了一种多模型鲁棒自适应控制器。通过设计多个含有非线性鲁棒项的辨识模型对系统进行在线辨识,并基于辨识模型设计相应的控制器。采用基于辨识误差的性能指标函数作为切换依据,选取最佳辨识模型及控制器,并把该控制器作为当前控制器,解决了传统自适应控制对参数自适应初值敏感的问题,提高了系统的瞬态响应性能。通过辨识模型中的非线性鲁棒项,减小了干扰、未建模动态等不确定非线性的影响。运用李雅普诺夫稳定性理论,证明了控制器的稳定性。实验结果表明,通过设计多个含有非线性鲁棒项的辨识模型,可以有效抑制建模不确定性的影响,提高系统跟踪精度,与MMAC相比,稳态精度提高了28%左右,验证了本文所提算法的有效性。


2 控制器的设计
2.1 辨识模型及参数自适应的设计
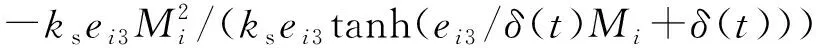
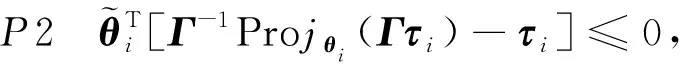
2.2 控制器的设计
2.3 切换策略的设计

2.4 控制性能及稳定性分析


3 实验结果及分析







4 结 论
