基于多元可靠性模型的复杂结构件危险点选取方法
2018-11-14胡杰鑫尹伟任俊刚孙维光谢里阳
胡杰鑫,尹伟,任俊刚,孙维光,谢里阳
(1.东北大学航空动力装备振动及控制教育部重点实验室,110819,沈阳;2.北京强度环境研究所,100076,北京;3.中车青岛四方机车车辆股份有限公司,266000,山东青岛)
随着科学技术的飞速发展,机械装备趋于大型化和复杂化,并且要求的安全服役寿命也越来越长。对于绝大多数复杂结构件而言,在其服役周期内,主要的失效模式并不是静强度失效,而是由交变载荷持续作用所导致的疲劳失效。因此,准确评估复杂结构件的疲劳寿命及可靠性,对于机械装备的服役安全和改进升级至关重要。
在预测复杂结构件的疲劳寿命及可靠性时,主流方法都是先确定复杂结构件上的薄弱部位,作为复杂结构件的危险点,而后结合材料性能计算获得危险点的疲劳寿命,即为复杂结构件的疲劳寿命。目前,多数学者在确定复杂结构件的危险点时,通常只是根据有限元分析的结果,选取应力集中或者应力最大的位置为危险点,利用此方法分析的复杂结构件包括高空作业平台[1]、动车组车体[2]、列车枕梁[3-4]、隧道掘进机刀盘[5-6]、航空发动机燃烧室[7]、飞机蒙皮[8]、客车骨架[9]、凿岩机活塞[10]、拖拉机车轴[11]等。复杂结构件危险点是否发生疲劳失效,不仅取决于应力集中或应力最大,还受到材料分散性、载荷作用次数、环境腐蚀等多种因素的综合影响。以应力集中或者应力最大为判据确定的复杂结构件危险点有可能并不是真正的危险点,例如:在1个复杂结构件上,不同部位、不同材料的抗疲劳性能不同,如果高应力的位置处恰好材料的抗疲劳性能也高,其寿命并不一定比低应力且抗疲劳性能也低的位置寿命短,这在带有焊缝的复杂结构件上表现得十分明显。
为了获得复杂结构件准确的疲劳寿命及可靠性评估结果,在确定危险点时需要综合考虑各种影响因素,如载荷不确定性、材料性能不确定性、载荷作用次数和材料强度退化等。因此,本文提出了基于多元可靠性模型的复杂结构件危险点选取方法,并以某型号地铁列车枕梁的疲劳可靠性评估为例,详细展示了计算过程。
1 多元可靠性模型
复杂结构件的疲劳可靠性指的是其在规定的服役条件下,疲劳寿命大于设计服役时间的概率。若已知复杂结构件在复杂随机载荷作用下的寿命分布,则其服役到t时刻的可靠性可以表示为

(1)
式中:h(τ)是复杂结构件在复杂随机载荷作用下的寿命分布函数,但实际上很难获得。
影响复杂结构件疲劳可靠性的因素有材料性能的不确定性、外界载荷的不确定性、规定时间内载荷的作用次数以及随载荷作用而发生的材料强度退化。传统的应力-强度干涉模型只考虑了强度和应力的不确定性,而且只适用于计算1次载荷作用下的可靠性。在传统模型下,可靠性的计算公式为
(2)
式中:g(s)为应力概率密度函数;f(S)为强度概率密度函数。
随着外界载荷作用次数的增加,理论上大载荷出现的次数会增多,因此复杂结构件的疲劳可靠性将随之降低,故在式(2)的基础上,考虑外界载荷作用次数对复杂结构件可靠性的影响,可靠性的计算公式可以表示为
(3)
式中:n为载荷作用次数,若n为随机变量,且为时间t的函数时,则载荷作用次数的发生率可以表示为
P(N=n)=ωn(t)
(4)
其中,ωn(t)为载荷作用次数的概率分布函数。
复杂结构件安全服役到时刻t的可靠性为
(5)
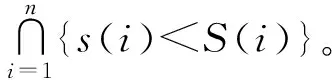
因此,在式(5)的基础上,考虑材料强度退化的可靠性模型为
(6)
目前,许多学者对材料强度退化已经进行了深入研究,并根据不同的研究对象,提出了多种剩余强度模型,但普适性的模型还有待进一步研究。
式(2)~(6)所考虑的应力不确定性只是复杂结构件某一载荷历程样本内部载荷峰值导致的应力分布,但不同的载荷历程对复杂结构件的可靠性影响也并不完全相同。因此,文献[13]对外界载荷的不确定性做了进一步区分,定义了载荷宏观不确定性(即载荷历程具有不确定性)和载荷微观不确定性(即同一载荷历程样本内部的载荷峰值具有不确定性)。在式(6)的基础上,文献[13]提出了综合考虑载荷宏观不确定性和微观不确定性的多元可靠性模型
(7)
式中:h(L)为以L标识的宏观载荷的概率密度函数;ωn(t,L)为以L标识的载荷历程样本的载荷作用次数的分布律;f(S)为强度概率密度函数;g(s,L)为以L标识的载荷历程样本的微观载荷(应力)的概率密度函数;S(i)表示载荷第i次作用时的材料剩余强度,本文所采用的材料剩余强度S(i)的具体表达式详见3.2节。
2 危险点选取思路
利用多元可靠性模型,可以全面地考虑载荷不确定性、材料性能不确定性、载荷作用次数和材料强度退化对复杂结构件危险点的疲劳寿命及可靠性的影响,据此提出的复杂结构件危险点选取方法的具体流程如图1所示。其中,潜在危险点选取为有限元计算确定的复杂结构件的应力集中部位;多元可靠性模型以获得的实际信息为基础,如材料强度的概率密度函数、宏观载荷的概率密度函数、微观载荷的概率密度函数、载荷作用次数分布律以及剩余强度模型;危险点为在复杂结构件的设计服役年限内,对其疲劳可靠性构成较大影响的点,即危险点的可靠性小于0.999 9。
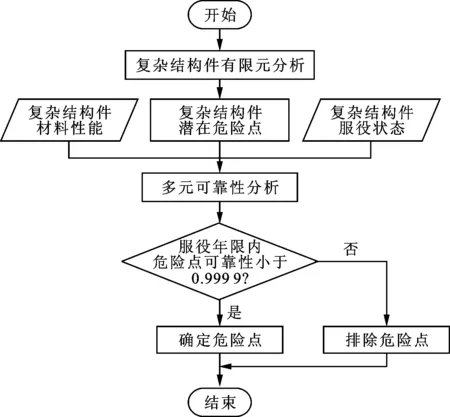
图1 复杂结构件危险点选取流程图
3 地铁列车枕梁危险点选取实例
以某型号未投入使用的地铁列车枕梁为例,利用本文提出的危险点选取方法,具体展示地铁列车枕梁危险点的选取及计算过程如下。
3.1 载荷不确定性
载荷不确定性包括载荷的宏观不确定性和微观不确定性。对于地铁列车枕梁而言:载荷宏观不确定性表现为同一型号的地铁列车在不同轨道运行的不确定性,由于不同的地铁轨道所处的地理位置不同,并且不同城市的地铁乘客数也存在很大差异,因此即使是同一辆列车在不同轨道上运行,所受到的载荷也存在明显的不确定性;载荷微观不确定性表现为地铁列车枕梁在同一线路上运行时所受载荷的不确定性,虽然列车运行在固定不变的轨道上,但每天的人流量并不完全相同,因此在地铁列车枕梁上的载荷也存在差异。
获得载荷不确定性的最好方法是统计同一型号列车的销售和使用情况,并对运行在不同轨道的地铁列车枕梁进行疲劳载荷实测。宏观载荷的概率分布根据在不同轨道上运行的同一型号列车的数量来确定,某一轨道的微观载荷概率分布则通过对该线路枕梁所受的疲劳载荷的实测结果来统计获得。由于该型号地铁列车枕梁并未投入使用,而且不同线路上地铁列车枕梁的应力实测数据也无法获得,因此,根据相关国际标准[14-18],同时参照沈阳地铁1号线的运营情况,利用泊松随机过程编制合理的地铁列车枕梁载荷谱。
地铁列车在运行过程中,枕梁将承受中心销载荷和空气弹簧载荷,而它们均为整车质量的函数。地铁列车整车质量由车身质量和乘客质量构成,设计载客量为226人、允许超员至290人的地铁列车,假设每位乘客体重为60 kg,则乘客质量的正常变化范围为0~13.56 t,约占车身质量20.5 t的1/2。根据《铁道车辆车体结构静载荷试验方法》[17]和《铁路机车车辆客车结构体设计一般要求》[18]的规定:在疲劳载荷未知的情况下可以将乘客数量变化作为载荷变化的来源。因此,在地铁列车枕梁算例中,将乘客质量变化作为引起疲劳载荷变化的主要因素。
泊松随机过程是一类较为简单的时间连续且状态离散的随机过程。地铁乘客数量每天都是从0开始,每站之间乘客增加数量相互独立,同时乘客数量增加是独立增量过程。因此,地铁乘客数量变化是一个泊松随机过程[19],且参数表示单位时间内到达地铁车站候车的平均乘客数量。某时刻沈阳地铁1号线各站乘客数见图2。
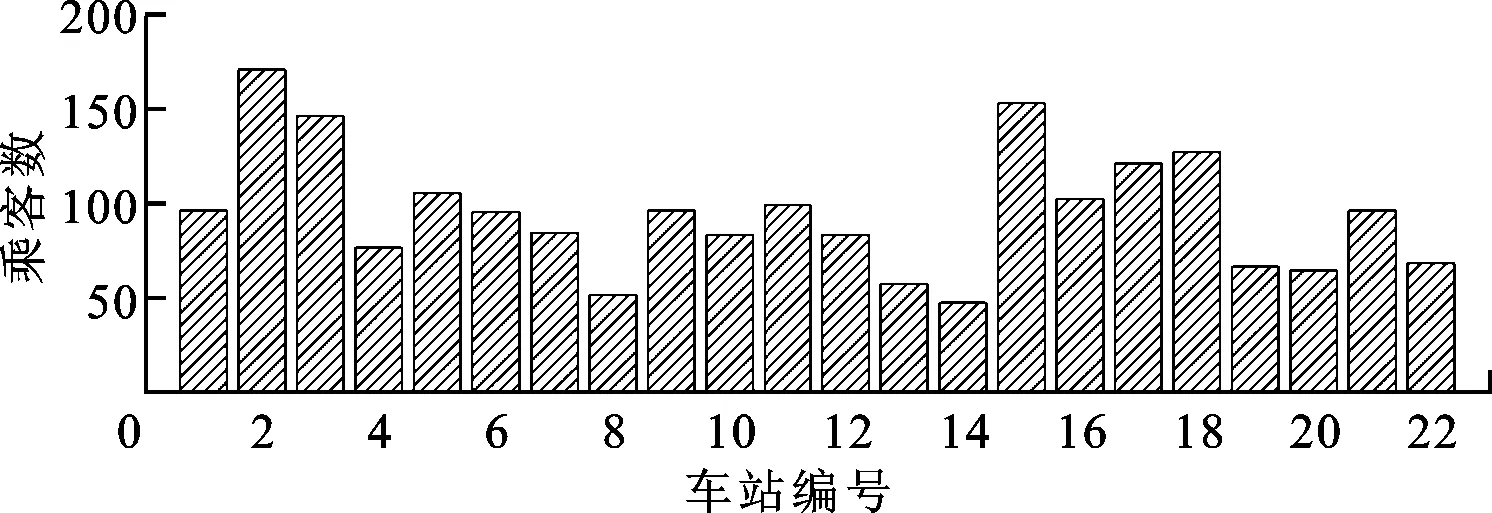
图2 某时刻沈阳地铁1号线各站乘客数
沈阳地铁1号线共22站,每天运行18趟,乘客数量变化396次。假设该地铁列车枕梁将会服役于国内10个城市的地铁线路,每天的乘客数量变化次数即为地铁线路车站数与每天运行数量的乘积,每站乘客的候车数可利用泊松随机过程来模拟,其参数与城市乘坐地铁的人口数相关。利用上述方法,产生了10种不同的乘客数量变化谱,作为该地铁未来服务于10个不同城市将会受到的模拟载荷谱,汇总的信息如表1所示。
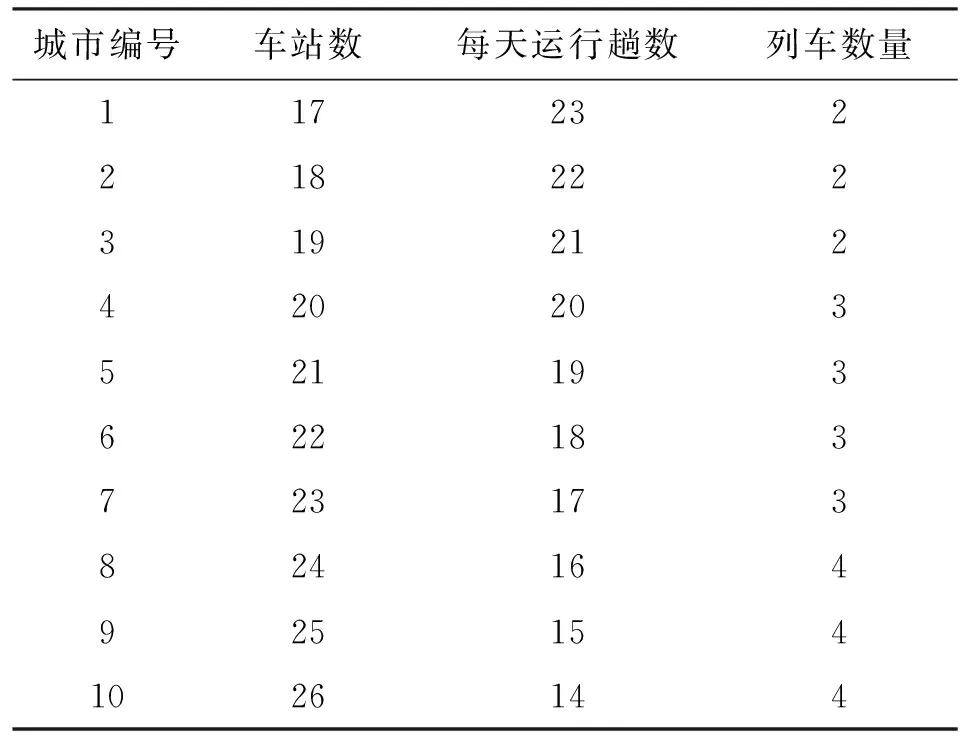
表1 10个城市地铁的模拟载荷谱
对某城市100天的乘客数量进行观察,取每天乘客数量的最大值统计获得的概率分布即为该城市地铁列车枕梁微观载荷的概率分布。泊松随机过程模拟产生并统计获得的10个城市的微观载荷概率分布如表2所示,而地铁列车枕梁在该市的宏观载荷概率为该市地铁线路上运行的列车数量占该型号列车总数的比例,每个城市的具体列车数量见表1。
地铁列车枕梁危险点的微观载荷(应力)与乘客数量之间的关系可以根据枕梁的理论载荷公式和有限元方法计算获得,在此不再赘述。
3.2 强度分布及退化模型
地铁列车枕梁结构件含有铝合金板材、型材和焊缝,虽然有限元分析结果显示最大应力主要出现在铝合金型材上,但由于其强度较高且抗疲劳性能较好,一般不会发生疲劳失效,因此本例以角焊缝为主要研究对象,选择的潜在危险点(应力集中部位)均位于角焊缝处。根据文献[20]对铝合金焊缝抗疲劳性能的研究,铝合金角焊缝的强度极限服从均值为193.25、标准差为9.61的正态分布。
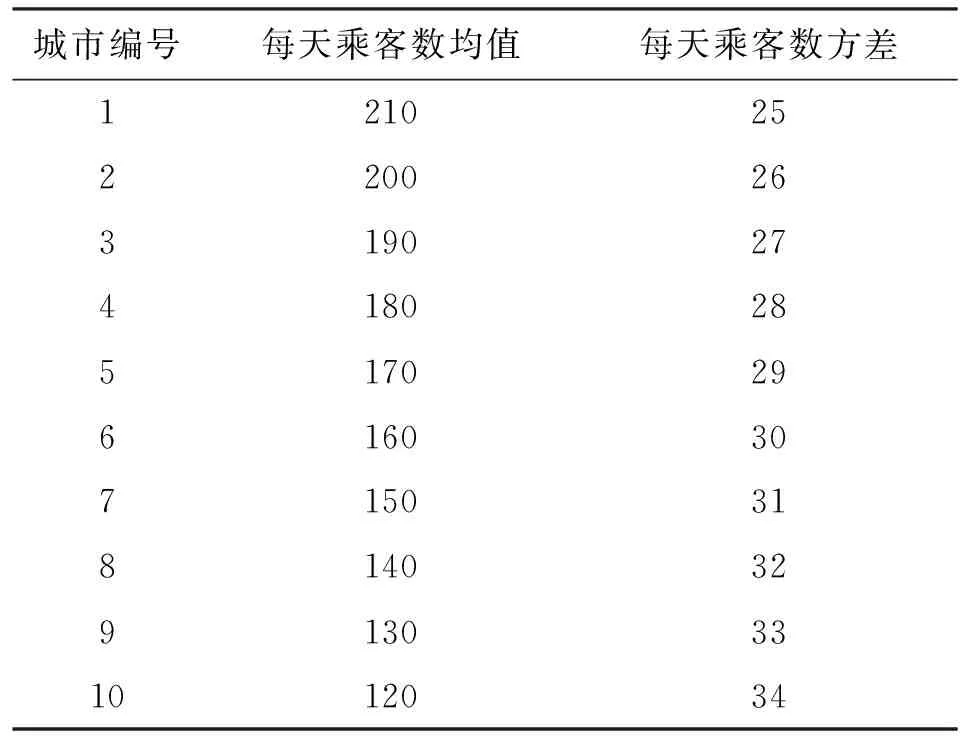
表2 10个城市地铁的微观载荷概率分布
随着地铁列车枕梁服役时间和载荷作用次数的增加,角焊缝的材料性能逐渐退化,剩余强度将会按某种规律降低,当低于所承受的正常工作应力时即发生疲劳失效。现假设本算例中角焊缝的剩余强度与载荷的作用次数为对数关系,具体表达式[13]为
(8)
式中:S(n)为应力作用n次后的剩余强度;S0为材料的初始强度;σmax为循环应力最大值;n为应力作用次数;Nf为σmax应力水平下的疲劳寿命。
由于式(8)只是一个非线性强度退化模型,而实际使用情况更加复杂。考虑到在复杂载荷历程作用下(如地铁列车乘客数量复杂多变),疲劳损伤的非线性效应有很大一部分将会相互抵消,并且有些材料及结构的剩余强度本身就是近似地按线性规律退化,因此,可将式(8)的非线性模型进行初级近似,用线性退化模型描述复杂载荷历程下的强度退化规律,表达式[21]为
S(n)=S0+(S0-σmax)[n/(N-1)]
(9)
当n=0时表示材料的初始状态,此时S=S0,S0为静拉伸强度极限;当n=N-1时(N为疲劳寿命),表示剩余强度已经达到了临界破坏状态,此时S=σmax,当应力比为-1时,σmax与应力幅σa相等。在本算例中,角焊缝的初始强度取为193.25 MPa,循环应力最大值为乘客满员时危险点处寿命为107次载荷循环时所对应的应力值。
由于地铁列车枕梁不同部位的应力比并不相同,在循环载荷作用下,即使是同种材料,其退化规律也会有差异,这主要是因为危险点处单位载荷循环所造成的疲劳损伤受平均应力影响。因此,在确定式(9)中的σmax时,需要考虑应力比(或者平均应力)的影响。通过研究平均应力对角焊缝处疲劳极限的影响,发现Goodman寿命直线的等效结果最准确[20]。Goodman寿命直线方程为
(10)
式中:σa为应力幅;σ-1为应力比为-1时的疲劳极限;σm为平均应力;σb为强度极限。
利用式(10)计算确定的潜在危险点寿命为107次载荷循环时的σ-1,即为该点在式(9)中的σmax。
3.3 载荷作用次数
本算例中造成角焊缝强度退化的载荷是在每天乘客较多时产生的,这样的载荷每天出现的概率服从泊松分布,其参数的含义为每天地铁列车枕梁大载荷出现次数的期望值。对于某一条确定的地铁线路,由于城市的发展,该线路上每天大载荷出现的次数会随着时间的推移而发生变化,但在此并不做考虑,仅假设大载荷每天出现次数的概率固定不变,载荷作用次数的分布律为
(11)
10个城市地铁的载荷作用次数见表3。
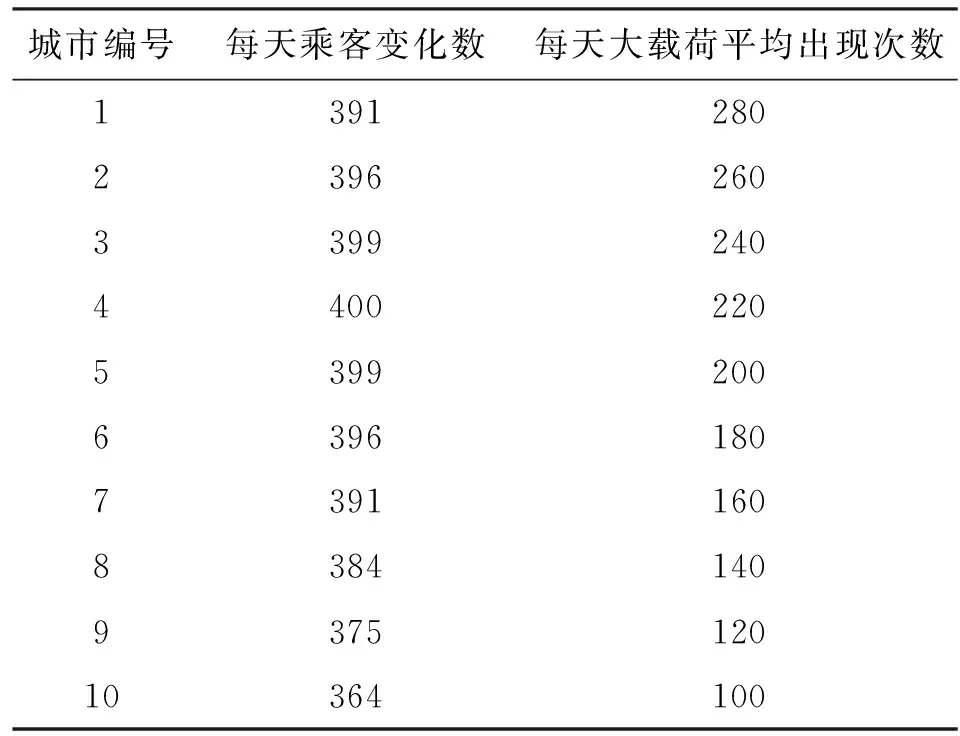
表3 10个城市地铁的载荷作用次数
3.4 列车枕梁潜在危险点
按照相关标准[14-18]对该地铁列车枕梁进行有限元分析,有限元计算模型如图3所示。其中,在最大载荷工况时,根据标准设计的中心销载荷为50 kN,空气弹簧载荷为110.57 kN。
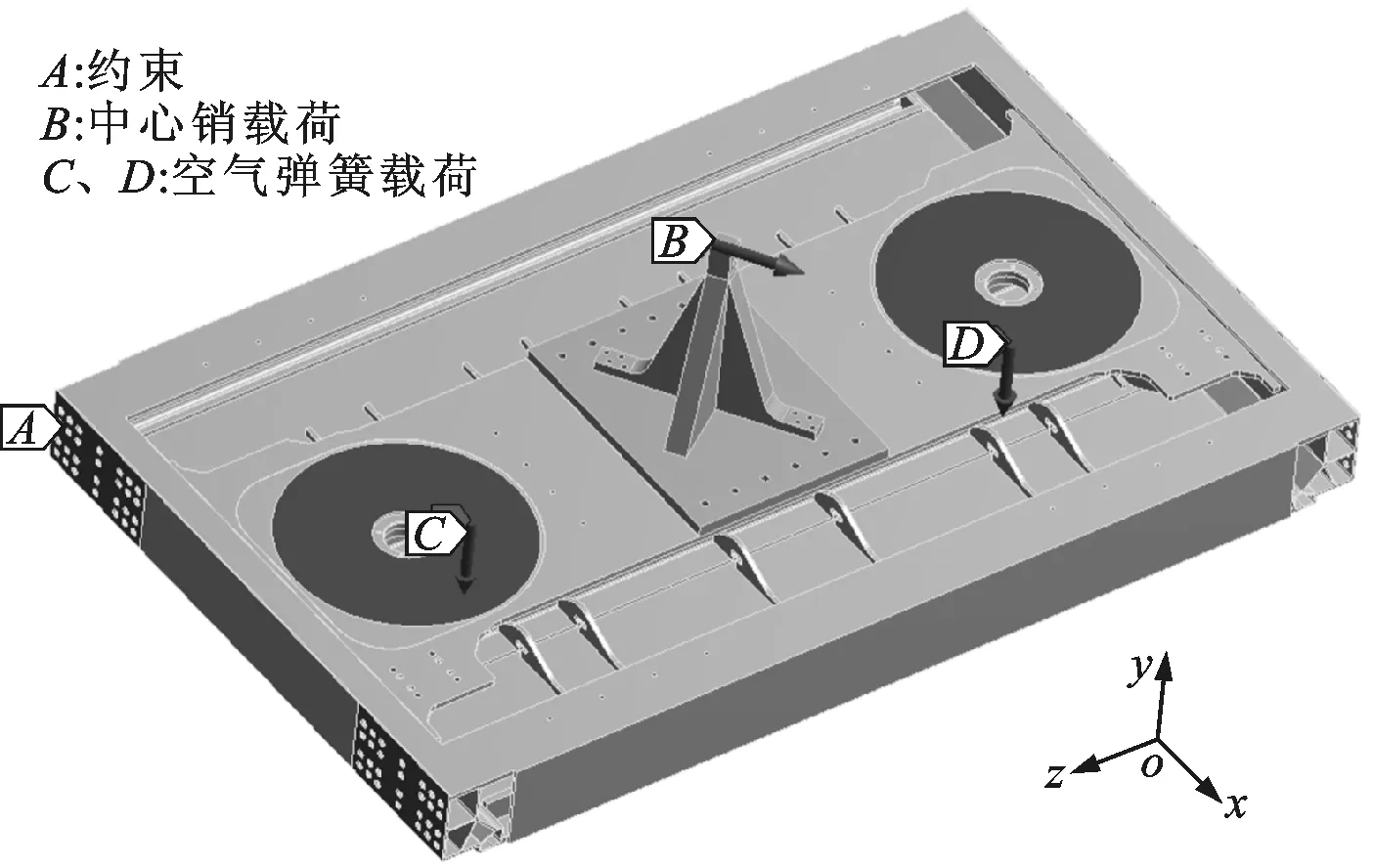
图3 列车枕梁有限元计算模型
根据有限元分析结果,从角焊缝处选取28个应力集中位置,并根据角焊缝p-S-N曲线[20],利用Gerber寿命图[12],对这些位置的疲劳寿命进行了评估,结果如图4所示。
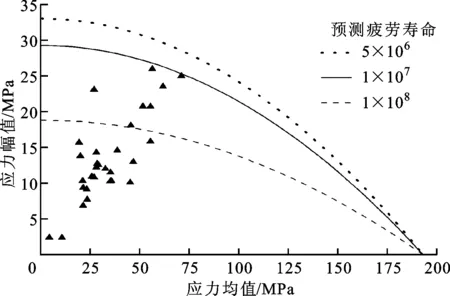
图4 存活率为99%时列车枕梁的Gerber寿命图
这28个应力集中位置均为地铁列车枕梁的潜在危险点,但本算例仅选取寿命较短的7个点(图4中预测疲劳寿命介于107和108次载荷循环之间)来讨论,具体位置如图5所示,其应力状态如表4所示。
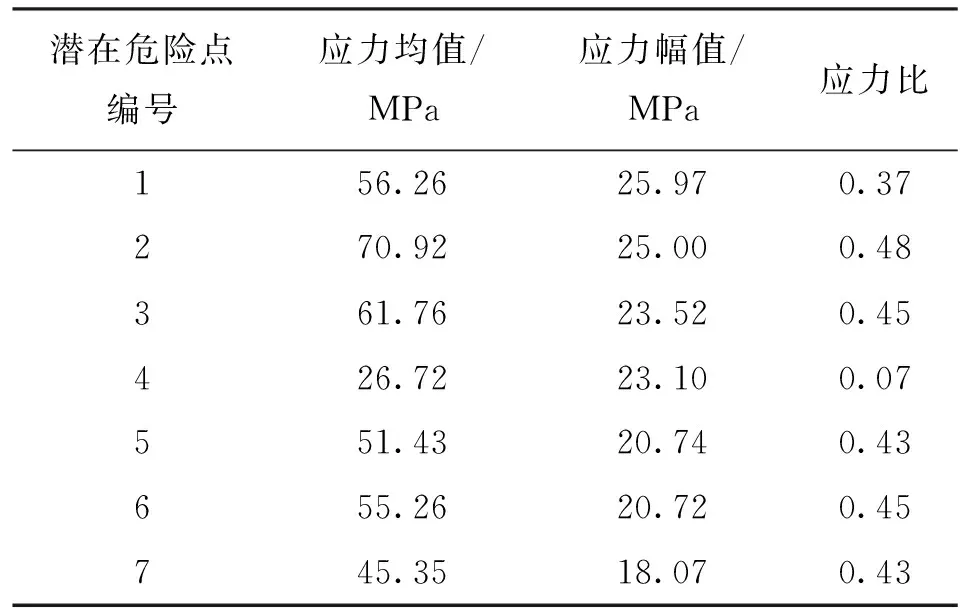
表4 潜在危险点应力状态
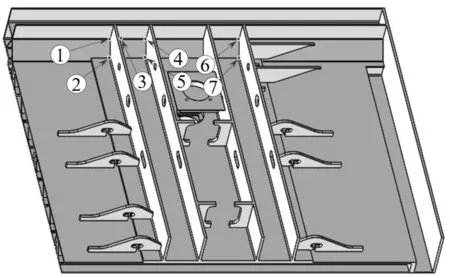
图5 列车枕梁7个潜在危险点的位置
3.5 列车枕梁可靠性
根据前文的分析与假设,本算例中危险点的多元可靠性模型为
(12)
式中:t为时间,单位为d,每年以365 d计算;l为城市编号;P(L=l)为城市l的宏观载荷概率;P(N=n)为载荷出现n次的概率;f(S)为强度概率密度函数;S((t-1)N(l)+i)为在城市l上运行第t天时的剩余强度;gl(s)为城市l的微观载荷概率密度函数。将相关参数代入式(12),分别计算地铁列车枕梁7个潜在危险点的可靠性,结果如图6所示,可以看出:当服役时间达到60 a时,点1的可靠性开始下降,点2和点3的可靠性分别在服役64 a和68 a出现下降,其余4点的可靠性始终约为1。
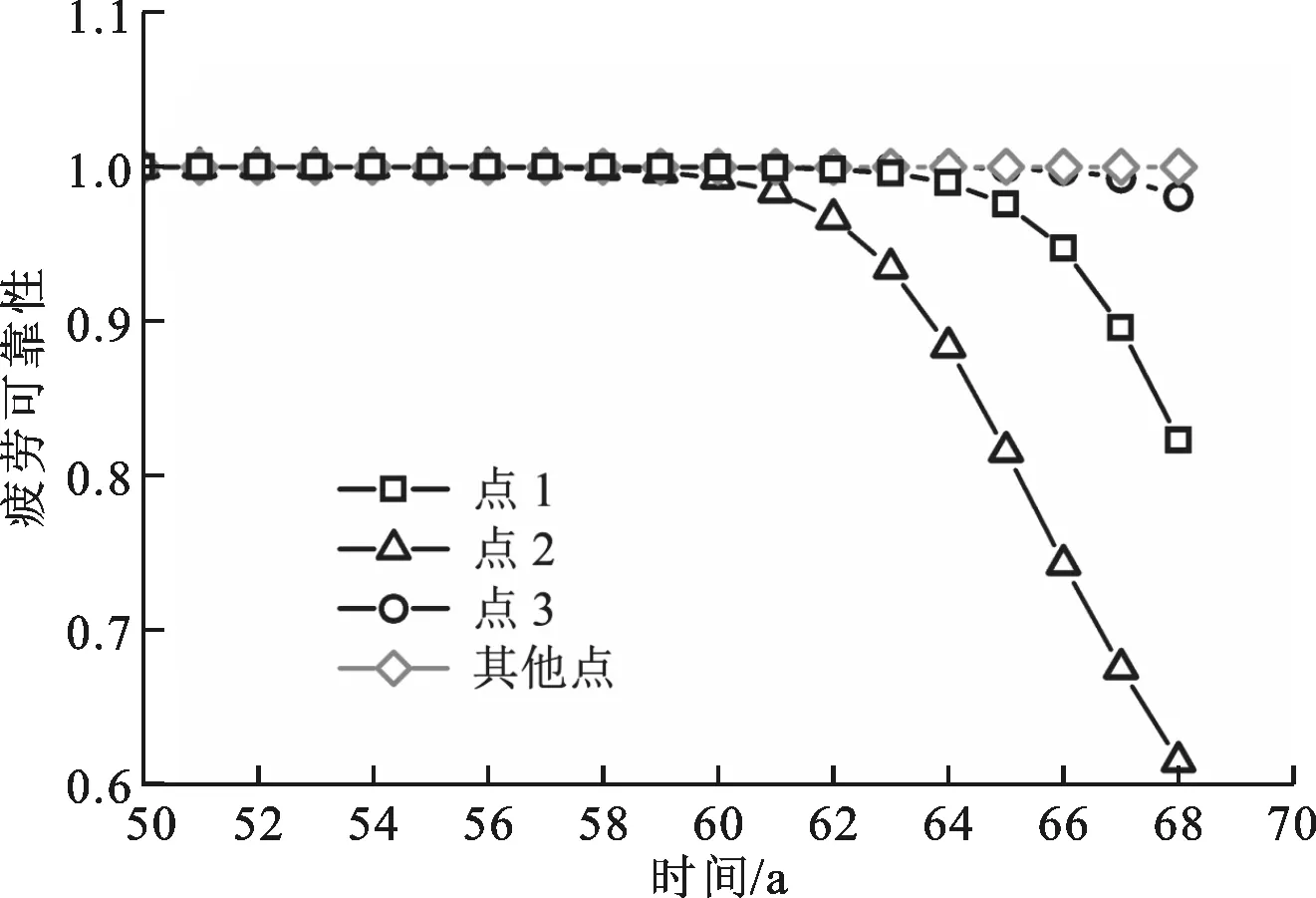
图6 潜在危险点的疲劳可靠性
根据图6中潜在危险点的疲劳可靠性信息,可假设该地铁列车枕梁是由x个潜在危险点构成的串联系统,据此来计算枕梁的疲劳可靠性,结果如图7所示。分析可知,潜在危险点1、2对地铁列车枕梁疲劳可靠性的影响较大,是地铁列车枕梁的真正危险点,而其他潜在危险点对枕梁疲劳可靠性的影响较小且可以忽略。同时,该地铁列车枕梁在假设的服役环境中,完全满足安全服役30 a的设计要求,并且服役60 a的累计失效概率仅为0.75%。
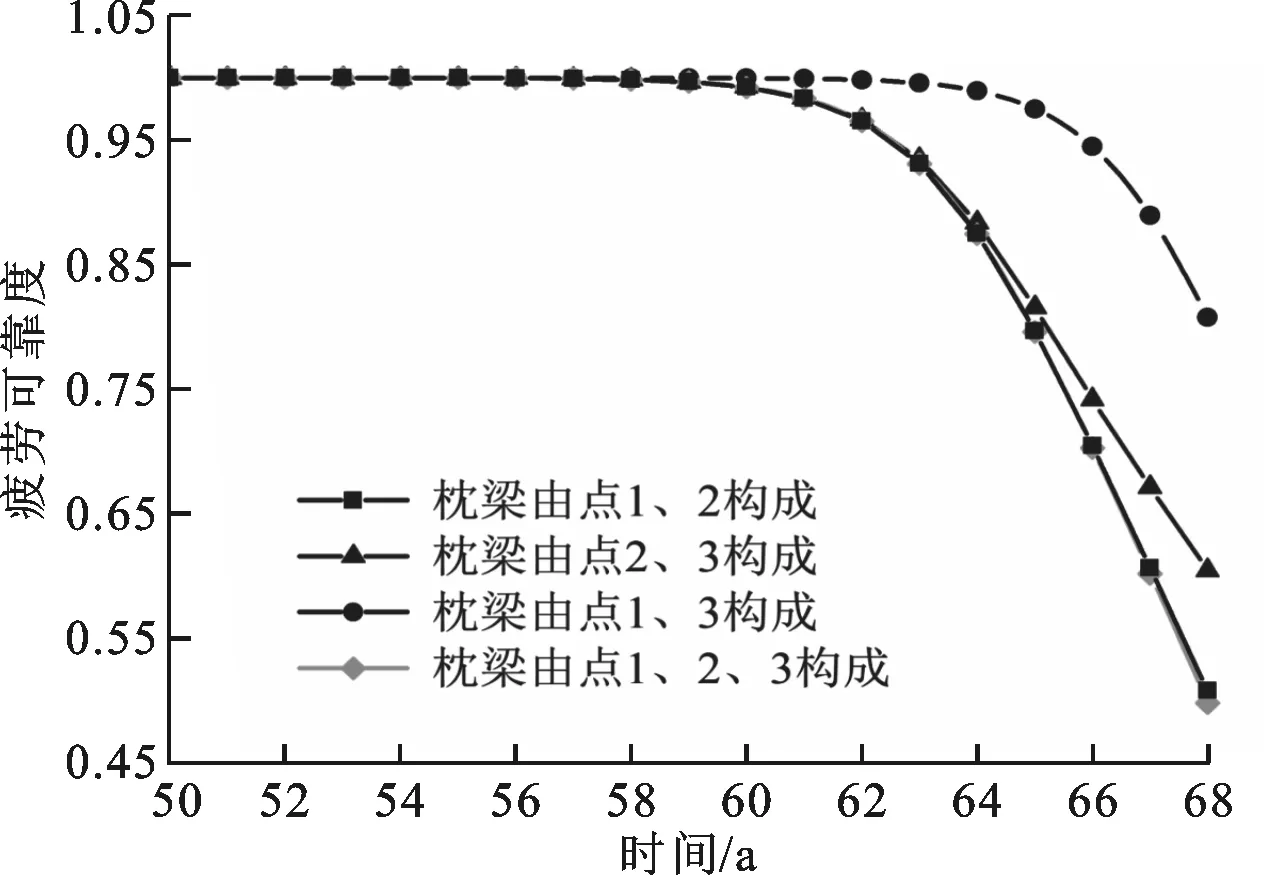
图7 地铁列车枕梁的疲劳可靠性
本算例只是对位于角焊缝处的危险点进行可靠性评估和选取,当复杂结构件上同时存在多种材料,并且应力分布很不均匀的时候,利用多元可靠性模型的危险点选取方法较传统的、仅仅以应力集中或者应力最大为依据的危险点选取方法具有更加明显的优势,且复杂结构件的疲劳寿命及可靠性评估结果也更加准确。
4 结 论
(1)从传统的应力-强度干涉模型出发,讨论了载荷作用次数、强度退化、载荷不确定性和强度不确定性等因素对复杂结构件疲劳可靠性的影响,建立了相应的多元可靠性模型,据此提出了用于评估复杂结构件疲劳寿命及可靠性的危险点选取方法。
(2)以某型号地铁列车枕梁为例,详细展示了基于多元可靠性模型的危险点选取过程。其中,根据地铁列车相关标准,并参照沈阳地铁1号线的运营情况,利用泊松随机过程编制了该地铁列车枕梁未来将服役的10条线路载荷谱,同时假设了载荷宏观不确定性和微观不确定性的相关参数。
(3)以应力集中为依据确定的28个潜在危险点中,经分析只有2个危险点对该地铁列车枕梁疲劳可靠性会产生较大影响。同时,枕梁在假设的服役环境中运行60 a的可靠性约为99.25%,完全满足设计要求。
