结合虚拟点的单元基光滑点插值法在结构动力学分析中的应用

张桂勇,陶东松,陈泽聪,陈毓珍

(1.大连理工大学船舶工程学院,116024,辽宁大连;2.大连理工大学工业装备与结构分析国家重点实验室,116024,辽宁大连;3.高新船舶与深海开发装备协同创新中心,200240,上海;4.中国船舶工业集团上海船舶研究设计院,201203,上海)

在工程问题中,结构的振动固有频率和动态响应是结构分析的基础,受到了人们的广泛重视。随着有限元法[1]在结构数值模拟方面的迅速发展,多种商业数值仿真软件被开发出来,成为工程技术人员进行结构分析的有力工具。但是,有限元法也存在一些固有问题[1],比如采用划分简便的线性三角形(四面体)单元求解时,得到的系统刚度过硬,精度较差,而对于精度较高的四边形(六面体)计算网格,在复杂的几何条件下常常难以自动划分质量较高的网格。

为解决上述问题,近年来发展出了一系列新的数值方法,如光滑有限元方法(S-FEM)[2-3]和光滑点插值方法(S-PIM)[4]。S-PIM基于G空间理论[5]和广义梯度光滑技术(GSM)[6],相较于刚度过硬的有限元方法,可以有效软化系统的模型刚度[7-10],进而提高计算性能。在各种S-PIM中,单元基光滑点插值法(CS-PIM)[11]的刚度软化程度介于点基光滑点插值法(NS-PIM)[12]与边基光滑点插值法(ES-PIM)之间[13],可在仅使用线性三角形(四面体)单元的情况下,得到令人满意的结果。

在各种CS-PIM中,采用四点插值模式(T4)的径向基光滑点插值法(CSRPIM-T4)计算精度较低。为提高计算精度,同时不增加计算成本,将一种引入虚拟点参与构造的浓缩RPIM形函数(Cd)[14]应用于上述方法,得到结合虚拟点的单元基光滑点插值法(CSRPIM-T4-Cd)。研究表明:在传统的虚拟点布置方式下系统刚度过软[14],导致求得的固有频率偏低并出现虚假的非零能模态;在动力学求解中,即使采用无条件收敛的直接积分法,如Newmark法,依然存在时间不稳定性问题。

针对传统虚拟点布置中存在的问题,本文通过改变虚拟点的布置,可使原本过软的系统刚度更加接近真实的刚度,从而提高计算精度。通过对一系列自由振动与受迫振动的算例进行计算,验证了该方法的精确性。

1 单元基光滑点插值法

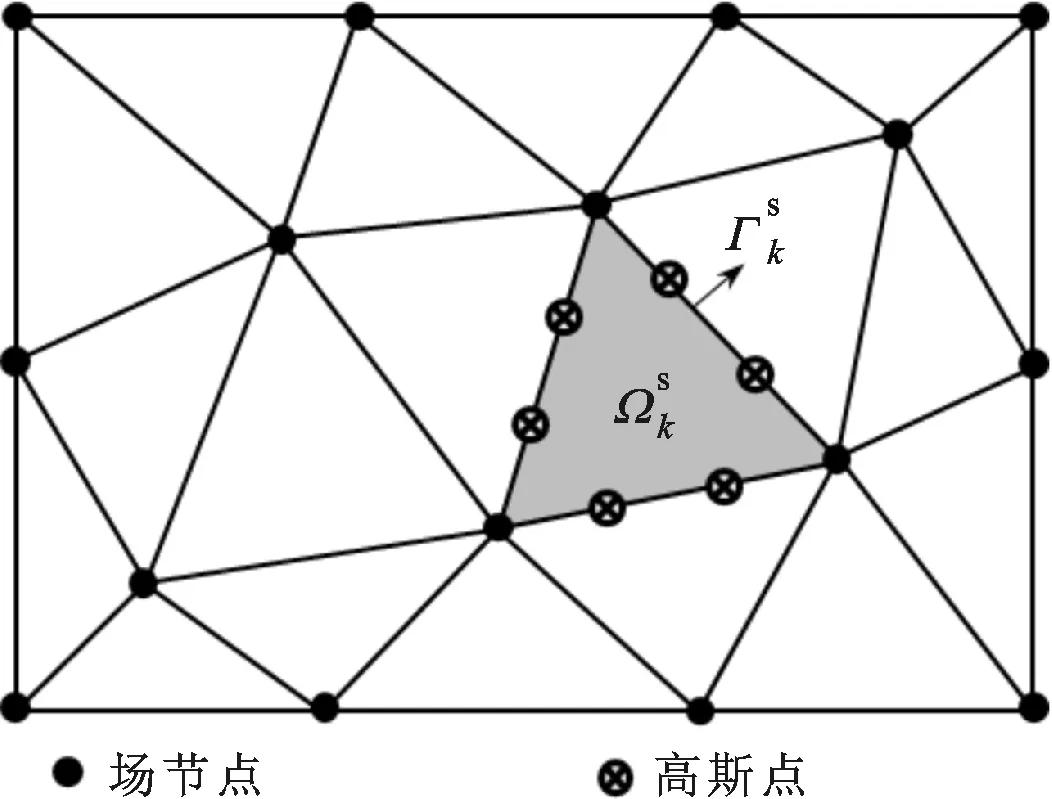
图1 基于三角形网格的单元基光滑域

根据GS-Galerkin弱形式(generalized smoothed Galerkin weak form)[4],可得

(1)

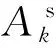
(2)

(3)

其中n1和n2分别对应光滑域边界的方向余弦。

位移场表示为

(4)

式中:Sn为用于插值的节点集;φI(x)为节点I处的形函数;Φ为由φI(x)组成的形函数矩阵;dI为节点I处的位移;d为由dI组成的节点位移矢量。

将式(3)、式(4)代入式(2),得

(5)

(6)

其中的各元素通过下式得到

(7)

采用高斯积分对式(7)进行计算

(8)

将式(4)和式(5)代入式(1),得

(9)

式中

(10)

(11)

(12)

式中Ne为背景网格的单元数目。因为背景网格同时作为局部应变光滑域,所以光滑域数目等于背景网格数。

2 浓缩形函数

2.1 RPIM形函数

采用添加了多项式基的径向基函数(RBF)作为插值形式,在局部区域内选取支持点进行插值模拟。此插值方法可使径向基PIM(RPIM)具备线性再生性,提高插值精度,同时避免了多项式基PIM的奇异性问题,方便支持点的灵活选取。使用如下插值形式来模拟位移场[15]

RT(x)a+PT(x)b

(13)

式中:n为局部区域内的支持点数;m为多项式基的项数,此处取线性完全多项式,即m=3;Ri(x)和ai分别表示径向基及其系数,Pj(x)和bj分别表示多项式基及其系数,形式如下

(14)

(15)

其中αc、q为复合二次形式径向基函数(MQ-RBF)的形状参数,取文献[16]中的推荐值,ri为支持点i和被插值点的径向距离,dc为问题域内节点的平均间距。

式(13)中有n+m个变量,若要使用支持域中n个点的值求解该式,需添加下面m个约束条件作为附加方程

PT(x)a=0

(16)

最后,求解得到对应于局部区域内n个节点位移的RPIM形函数[15],形式如下

Φ(x)={φ1(x),φ2(x),…,φn(x)}

(17)

2.2 支持点的选取方式

2.2.1 边基T4选点模式 在单元基光滑点插值法中,光滑域为三角形背景单元,光滑域的边界即三角形的边。边基T4选点模式采用基于边与场节点位置关系的方法来寻找支持点。

如图2所示,对内部边上的点,选取与该边相邻的2个三角形的4个顶点作为支持点,对问题域边界边上的点,选取该边的2个顶点作为支持点,可以确保边界条件的正确施加。

(a)内部边的T4选点模式

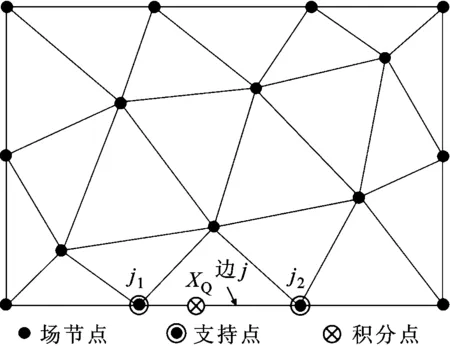
(b)边界边的T4选点模式图2 基于边的T4选点模式

2.2.2 加入虚拟点的边基T4选点模式 RPIM形函数常需要较多支持点来保证其精确性[14],但这又会降低计算效率,而使用虚拟点可以在不增加自由度数量的前提下提高形函数的模拟精度。

传统的虚拟点布置方式为:基于边基T4选点模式,在相邻的4条边的中心引入4个虚拟节点,如图3a所示,其坐标值由下式求得

(18)

(a)加入4个虚拟点

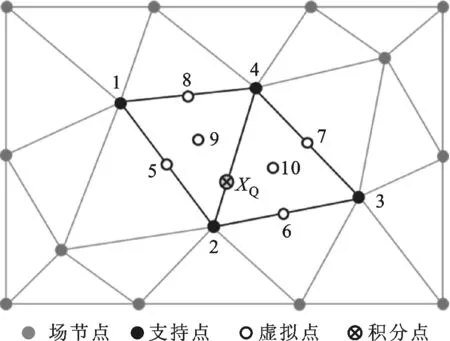
(b)添加6个虚拟点图3 加入虚拟点的内部边T4选点模式

研究[14]发现,引入4个虚拟点计算得出的系统刚度阵过软。本文采用一种新的虚拟点布置方式来改善形函数的模拟精度,如图3b所示,基于传统的虚拟点布置方式,在相邻的2个单元的形心处再引入2个虚拟点(即点9和10),其坐标值为

(19)

2.3 浓缩的RPIM形函数

2.3.1 CSRPIM-T4-Cd4形函数 使用4个真实场节点(1～4)和4个虚拟点(5～8)共8个支持点进行插值,可得浓缩前的RPIM形函数

Φs(x)={φ1(x),φ2(x),…,φ8(x)}

(20)

计算点处的位移可以表示为

(21)

虚拟点的位移可以通过真实场节点的位移线性插值得到

(22)

将式(22)代入式(21),可以得到

(23)

浓缩后的RPIM形函数可以表示为如下形式

(24)

2.3.2 CSRPIM-T4-Cd6形函数 与前面相似,使用4个真实场节点(1～4)和6个虚拟点(5～10)共10个支持点进行插值,可得浓缩前的RPIM形函数

Φs(x)={φ1(x),φ2(x),…,φ10(x)}

(25)

虚拟点位移由真实场节点位移线性插值得到

(26)

同样地,可以得到在引入6个虚拟点后的浓缩RPIM形函数

(27)

3 结构动力问题求解

3.1 系统离散方程

离散的动力问题GS-Galerkin弱形式[4]为

(28)

式中:Ω为问题域;D为材料弹性矩阵;tΓ为自然边界Γt上的外力向量;b为体力向量;c为阻尼系数;ρ为质量密度。

将式(4)和式(5)代入式(28),得

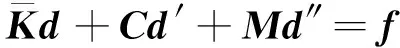
(29)

式中:C为阻尼矩阵;M为质量矩阵;f为力矢量。

(30)

(31)

(32)

质量矩阵采用动力问题中常用的集中质量阵,将单元质量集中到各个节点形成对角阵的形式,使方程便于求解。

3.2 自由振动

对于自由振动,不考虑阻尼和外力的影响,式(29)可简化为

(33)

式(33)的通解可以写成

d=dAexp(iωt)

(34)

式中:dA为位移幅值;t为时间;ω为自然频率,可由下式求得

(35)

3.3 受迫振动

受迫振动需要考虑阻尼以及外力的影响。采用瑞利阻尼,表达式为

(36)

式中α和β为阻尼系数。

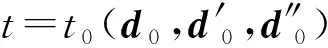
(37)

(38)

(39)

以上基于二维三角形单元的CSRPIM方法,可以扩展到基于四面体单元离散的三维问题[4]。在三维问题中,通过基于四面体单元的梯度光滑技术,将基于四面体的局部积分转化为基于四面体各个三角形面的积分;对于各个积分点的插值,同样采用径向基单元点插值法,在基于面的插值点选择模式基础上,通过在相邻四面体边线及形心布置虚拟点,达到提高插值精度、改变模型刚度、进而提高数值计算准确性的目的。

4 分片试验

通过标准分片试验可以验证本文方法能否收敛于准确解,它要求该分片内部的所有节点在机器精度上与分片的边界节点满足相同的位移函数[1]。

使用图4所示的背景网格来验证本文的数值方法,单位面积的方片由132个分布节点划分成222个单元。

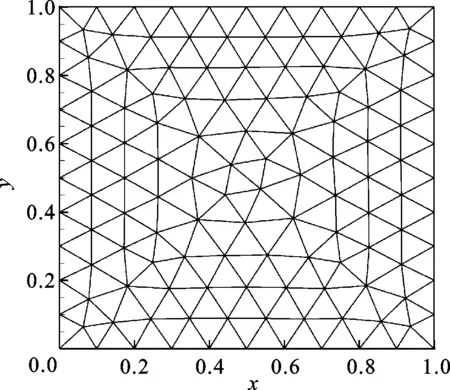
图4 132个节点离散的方片

在所有的边界节点上施加如下线性位移

ux=0.6x;uy=0.6y

(40)

计算精度用如下位移误差模来表示

(41)

式中:上角标“ana”表示解析解,“num”表示数值解;Nn为总节点数。

采用标准分片试验计算得到的位移误差模如下:CSRPIM-T4-Cd4的位移误差模为6.834 517 3×10-12,CSRPIM-T4-Cd6的位移误差模为3.742 340 5×10-11。以上结果显示,使用2种浓缩形函数的CSRPIM均能通过分片试验。

5 数值算例

5.1 连杆的自由振动

对一连杆进行自由振动分析。连杆尺寸如图5所示,完全约束左侧半径为1.0 cm的大孔内表面。

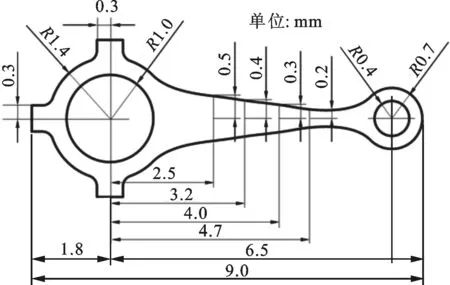
图5 连杆的几何尺寸

采用平面应力计算状态,材料参数为:杨氏模量E=10 GPa,泊松比ν=0.3,质量密度ρ=7.8×103kg/m3。用含633个不规则节点、1 010个单元的三角形背景网格离散该问题域,并应用ANSYS有限元软件以十分细密的四节点四边形单元(21 923个节点,21 146个单元)计算得到模态参考解。

表1为3种方法求解出的前10阶固有频率以及各阶频率的相对误差,同样可以看出:FEM-T3的固有频率偏高,系统刚度过硬;CSRPIM-T4-Cd4的固有频率偏低,系统刚度过软;CSRPIM-T4-Cd6的精确度最高,最接近真实刚度。表2是2种虚拟点布置方式求得的固有频率和模态振型与参考解的比较,从中可以看到:CSRPIM-T4-Cd4由于刚度过软,求解得到的固有频率偏低,且在高阶时存在虚假的非零能模态(加框振型);CSRPIM-T4-Cd6能够精确地模拟系统刚度,得到准确的固有频率和振型。

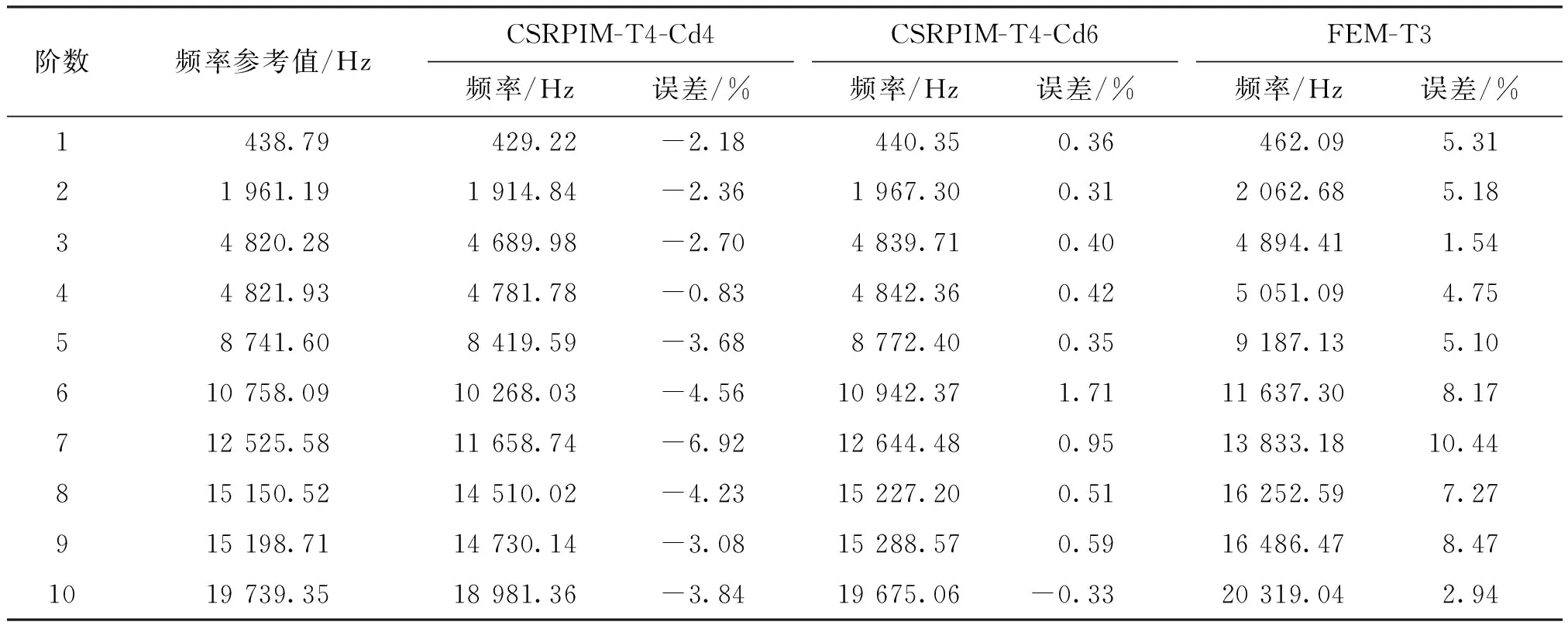
表1 3种方法计算的连杆前10阶固有频率及其误差

表2 连杆的模态振型及固有频率

5.2 悬臂梁的受迫振动

悬臂梁如图6所示,长L=48 m,宽D=12 m,厚t=1.0 m,自由端受到y方向的均布载荷p=1 000g(t)。悬臂梁为平面应力状态,计算参数取:杨氏模量E=30 MPa,泊松比ν=0.3,质量密度ρ=4.0 kg/m3。本例以200个不规则节点离散该问题域;采用瑞利阻尼,2个参数为α和β;应用Newmark法求解动力问题方程,取θ=0.5。此时,所采用的方法无条件稳定。

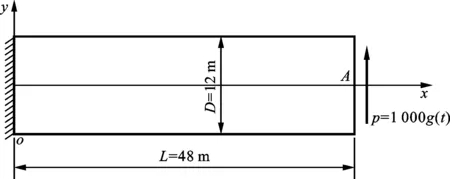
图6 悬臂梁计算模型

在相同的背景网格下,应用2种浓缩形函数的CSRPIM-T4-Cd和FEM-T3分别计算该算例,并以有限元软件用十分精细的(96×24)四边形单元计算的结果作为参考解,取梁自由端中点A的y方向位移绘制位移时间历程曲线,对这3种方法进行比较。

取载荷函数g(t)=cos(ωt)(N/m2),频率ω=13.5 rad/s,不考虑阻尼的影响(α=0,β=0)。图7展示的是A点的y方向位移时间历程曲线,时间范围为2 s,采用小时间步长(Δt=1 ms)。可以看出,CSRPIM-T4-Cd6的解与参考解十分接近,计算精度很高。为验证此方法的时间稳定性,在20 s范围内采用较大时间步长(Δt=5 ms),计算的位移时间历程如图8所示,可以看出此时计算结果稳定,仍然可以得到稳定的数值解。

图7 余弦载荷下A点在2 s内的位移

图8 CSRPIM-T4-Cd6计算的余弦载荷下A点在20 s内的位移

6 结 论

本文应用浓缩形函数的单元基光滑点插值法求解二维固体动力学问题。为验证方法的性质,进行了一系列自由振动和受迫振动的数值计算,得到如下结论:

(1)CSRPIM使用2种形式的浓缩形函数均能通过标准分片试验,且均可以收敛于真实解;

(2)CSRPIM-T4-Cd6方法能够准确地模拟系统刚度,为动力学问题提供十分精确且稳定的解;

(3)CSRPIM-T4-Cd4方法计算的系统刚度过软,模态分析中出现了虚假模态,存在时间不稳定的问题。

(4)虚拟点的加入与浓缩形函数的使用没有引入额外的系统自由度,相比传统的CSRPIM-T4方法不会增加计算成本。

(5)在可以自动划分问题域的线性三角形背景网格上,CSRPIM-T4-Cd6方法能够提供精度很高的计算结果,十分适合解决实际工程问题。