无序多视角点云的自主配准方法

徐思雨,祝继华,姜祖涛,郭瑞,李垚辰

(西安交通大学软件学院,710049,西安)

点云配准问题是在计算机视觉[1-3]和移动机器人[4]等研究领域中的基础问题。根据待配准点云数,该问题可分为双视角和多视角点云配准两种类型。

双视角配准是多视角配准的基础,其实质是通过定义相似性测度函数,并建立两帧点云之间点的对应关系以计算最优的变换关系。Besl等提出了基于迭代求解思想的迭代最近点(ICP)算法[5],对于解决刚体配准问题,该方法具有精度高和速度快的特点,但它不能解决缺失点云配准问题且具有局部收敛性。为了解决缺失点云配准问题,Chetverikov等提出了裁剪ICP算法[6],该方法在原始ICP算法的基础上,通过引入重叠百分比系数去除非重叠区域以准确地计算双视角配准结果。为了解决局部收敛问题,粒子滤波[7]和遗传算法[8]均被用于搜索全局最优的配准结果,但这类方法的计算量较大。有的学者提出一些基于特征匹配的双视角配准方法[9-10],此类方法通过从待配准的点云中提取并匹配特征,以快速计算双视角点云之间的刚体变换关系。

给定多视角点云集,多视角点云配准的目标是计算各点云和基准点云之间的刚体变换关系。与双视角点云配准问题相比,多视角点云配准问题需要求解的参数较多。解决此问题最简单的方法是顺序配准法[11],该方法通过不断地将两帧点云进行配准再合并以实现多视角配准结果,此方法虽然简单但存在累积误差问题。为了消除累积误差,Zhu等提出逐步求精的配准方法,该方法顺序遍历基准帧以外的各帧点云,并将所遍历的点云与其他点云构造的模型进行双视角配准,以修正单帧点云的多视角配准参数[12];Govindu等提出了基于运动平均算法的多视角配准方法[13],该方法将所有可获得的双视角配准结果作为输入,利用基于李群的运动平均算法计算多视角配准参数;Guo等给双视角配准结果赋予代表可靠度的权值,并提出了权重运动平均方法,以提高多视角配准结果的精度[14];Arrigoni等提出了基于低秩稀疏矩阵分解的多视角配准方法[15],该方法利用双视角配准结果构造矩阵,并利用低秩稀疏矩阵分解方法近似得到低秩矩阵,以便恢复获得多视角点云配准结果;Georgios等将多视角配准问题转化成聚类问题,通过利用期望最大化(EM)算法估算高斯混合模型(GMM),以实现聚类及多视角配准参数的计算[16],但该方法需要求解的参数较多,故算法的效率较低。

虽然前述方法可获得较好的多视角点云配准结果,但它们需要外界提供可靠的多视角配准初始值。为了获得多视角配准的初始值,Daniel等提出了全自主的多视角点云配准方法[17],该方法首先计算所有双视角配准结果,然后通过设计相容性准则找出可靠的双视角配准结果以分析获得多视角配准结果,由于该方法需要计算点云集中所有双视角点云的配准结果,故效率较低。Zhu等提出了基于生成树的多视角点云配准方法[18],该方法基于广度优先的搜索方式,利用所设计的判定准则寻找可靠的双视角配准结果创建生成树以获得多视角配准结果,由于大部分双视角点云之间的重叠百分比(点云重叠区域的点数占总点数的比值)较低,需进行多次双视角配准才能创建出完整的生成树,故基于生成树方法的效率有待进一步提高。

针对多视角点云配准问题,本文提出了基于特征匹配的多视角点云全局配准方法。该方法选取可靠的特征描述子快速实现双视角配准;设计合理的判定准则判别双视角配准结果的可靠性;提出有效的模型扩展方法,利用可靠双视角配准结果进行点云模型的扩展。通过采用交替地执行双视角配准、配准结果判别和模型扩展的方式,实现无序多视角点云的全局配准。

1 裁剪ICP算法

给定具有非重叠区域的双视角点云,分别包含Np个点的数据点云P和Nq个点的模型点云Q其中pi表示P中的第i个点,qj表示Q中第j个点。设Px表示重叠区域的数据点云上的点所组成的子集,重叠百分比x定义为和Np的比值,其中表示子集Px所包含的点数。定义裁剪均方误差

(1)

式中:R与t表示刚体变换中的旋转矩阵和平移变量;(pi,qc(i))表示模型点云和数据点云在重叠区域的具有对应关系的点对。双视角配准问题可表示为如下的最小化问题

(2)

式中λ是预设的参数,λ=2。

给定初始刚体变换(R0,t0),裁剪ICP算法采用交替迭代的思想求解最优的配准参数,且第k次迭代包含以下步骤。

步骤1基于当前刚体变换,建立点的对应关系

i=1,2,…,Np

(3)

步骤2根据当前点对关系,计算第k次迭代中的重叠百分比xk和子集Px

(4)

步骤3更新刚体变换关系

(5)

迭代执行步骤1～3,直到迭代步数达到预设的上限K或|ψk-ψk-1|<ε(ε为任意小的正数),即可停止迭代输出最优的配准参数(R,t)。与原始ICP算法相似,裁剪ICP算法也具有局部收敛性,但是为获得可靠的双视角配准结果,需要外界提供较好的配准初始值。

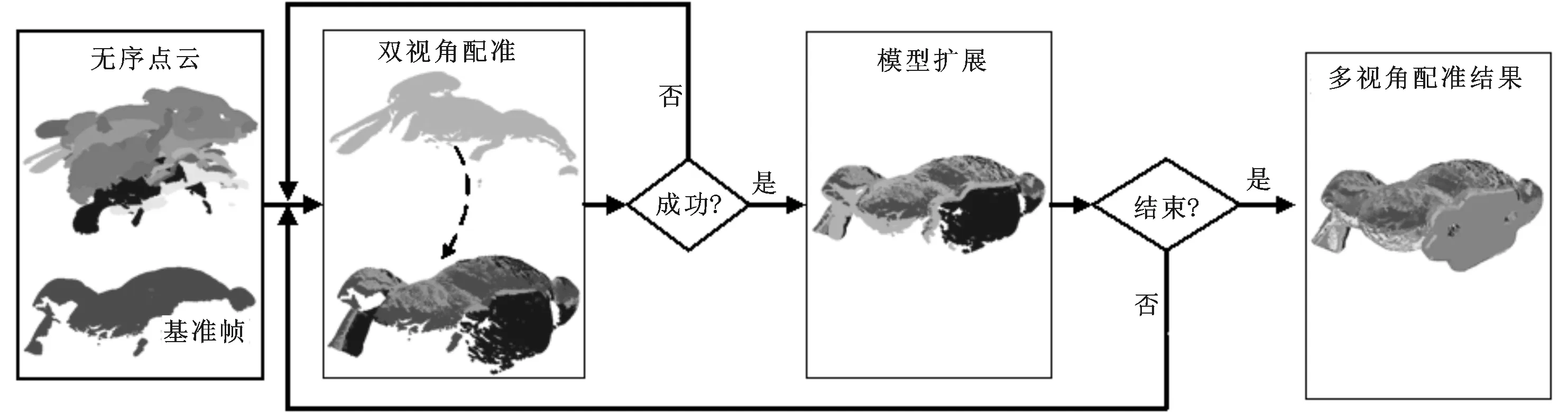
图1 无序多视角点云配准方法框架图

2 无序多视角点云全局配准

为了实现无序多视角点云的全局配准,本文提出了如图1所示的解决方法。该方法选定基准帧作为初始模型点云,顺序遍历点云集里的每一帧点云,然后利用双视角配准方法将所遍历的点云与模型点云进行配准,通过设计有效的判定准则,将判别出的可靠双视角配准结果用于模型点云扩展,直到全部点云被加入扩展模型中。

2.1 基于特征匹配的双视角配准

为了解决双视角配准问题,已有各种局部收敛的方法。在给定配准初始值时,这些方法可以计算出两个点云之间最优的刚体变换。然而,在无序多视角点云配准问题中,双视角配准初值是未知的,因此需要可实现全局配准的双视角配准方法。

Lei等提出了基于特征匹配的双视角全局配准方法[10],该方法先对原始点云进行降采样,以降采样获得的每个点为中心定义4个具有不同半径的圆球,接着利用球内所包含的原始点云,计算该点的4组法向量和特征值向量,并用9维的特征值差向量D和12维的法向量N作为特征描述子。由于特征值差向量具有旋转不变形性,可基于欧氏距离最近的原则建立简单的特征对应关系,随后将每个特征对作为种子匹配对,通过检验其他特征点与种子特征点之间的距离差和法向量夹角,选取兼容的特征匹配对形成特征匹配对集。为了消除错误的匹配对,可进一步利用随机一致性算法对匹配对集中的特征对进行筛选,选出可靠特征对确定双视角配准结果。由于种子匹配对不一定可靠,因此需要遍历全部种子匹配对,如果利用该种子点匹配对所找的相容特征匹配对数较少,则直接丢弃,否则需要采用随机一致性算法进行后续处理以确定双视角配准结果。最后,比较所有配准结果所对应的裁剪均方误差选出最可靠的双视角配准结果。

与原始点云相比,降采样后的特征点数较少,根据特征点所计算出的双视角配准结果精度有限。为提高配准结果精度,本文利用裁剪ICP算法对基于特征点匹配所求出的双视角配准结果进行了修正,以获得更好的双视角配准结果。

2.2 配准结果评判的设计

为了获得精确的扩展模型,需要选取可靠的双视角配准结果,为此必须设计有效的判定准则。

在多视角点云配准问题中,每对点云之间存在非重叠区域甚至无重叠区域。对于重叠百分比较高的双视角点云,裁剪ICP算法可准确地找出两点云之间的重叠区域,并计算出可靠的配准参数;对于具有低重叠百分比或无重叠区域的双视角点云,裁剪ICP算法会找出虚假的重叠区域,并计算出不可靠的配准参数。图2给出了具有不同重叠百分比的双视角点云配准结果,其中图2a所示的双视角点云具有较高的重叠百分比,图2b所示的双视角点云分别来源于兔子模型的正反面,具有较低的重叠百分比。由图2可知,可靠的配准结果使得位于重叠区域的点对误差距离较小,而不可靠的配准结果造成虚假重叠区域的点对误差距离较大,因此可将裁剪ICP算法所确定的重叠区域内的点对误差,即裁剪均方误差E,作为判定配准结果可靠性的依据。

(a)可靠的配准结果 (b)不可靠的配准结果

对于相同的数据点云和配准结果,裁剪均方误差会受模型点云点密度的影响。图3给出了模型点云点密度对裁剪均方误差的影响。由图3可知,低密度的模型点云将导致裁剪均方误差增大,高密度的模型点云有利于降低裁剪均方误差。根据裁剪均方误差受模型点云点密度之间影响的现象,本文给出如下双视角配准结果的判定准则

(c) 可靠的配准结果 (d) 不可靠的配准结果的横截面图 的横截面图图2 双视角配准结果的横截面图

(6)

式中:E为双视角配准结果所对应的裁剪均方误差;dM为模型点云的平均密度;a为设定的常数。如果E满足式(6),则可判定双视角配准结果较可靠,否则为不可靠。

为了改善判定准则,当获得一部分可靠的多视角配准结果后,可将这些配准结果所对应的均方误差的均值加入判定准则,即

E≤max(adM,bmE)

(7)

式中mE表示可靠配准结果裁剪均方误差E的平均值。参数a和b的选取将在实验部分进行讨论。

(a)低分辨率模型

(b)高分辨率模型图3 模型点云的分辨率对裁剪均方误差的影响

2.3 点云模型的扩展

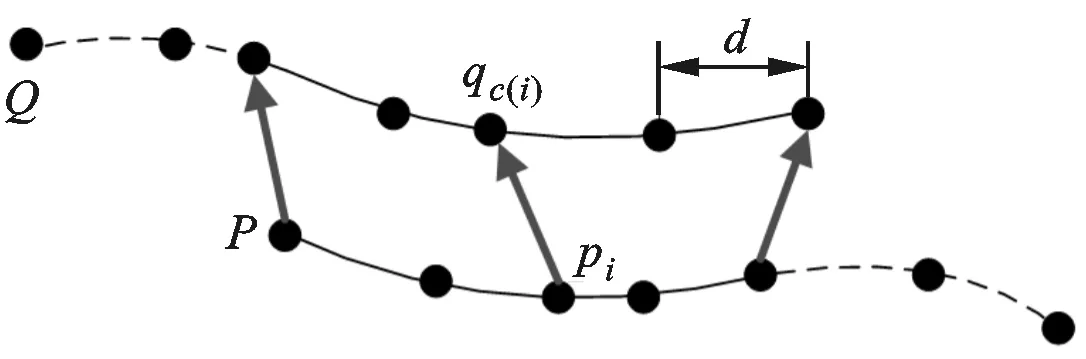
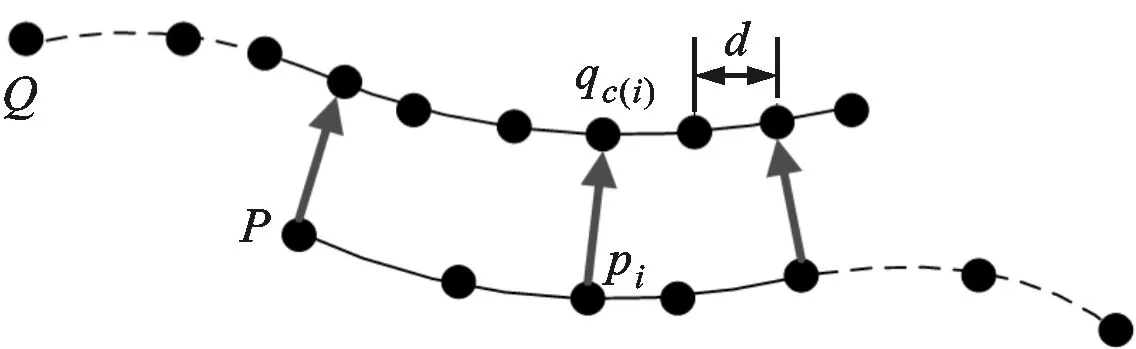
根据本文所设计的判定准则可判别双视角配准结果是否可靠,对于可靠的双视角配准结果则需要进行模型扩展。由于模型形状的点云密度会影响后续双视角配准的裁剪均方误差,为了保证判定准则的有效性,需要尽量保持模型点云密度的恒定性。为此,本文设计如图4所示的模型扩展方法。

利用双视角结果(R,t)将数据点云进行变换,以获得变换后的数据点云P′

P′{Rpi+t

(8)

(a)扩展前建立的点对关系

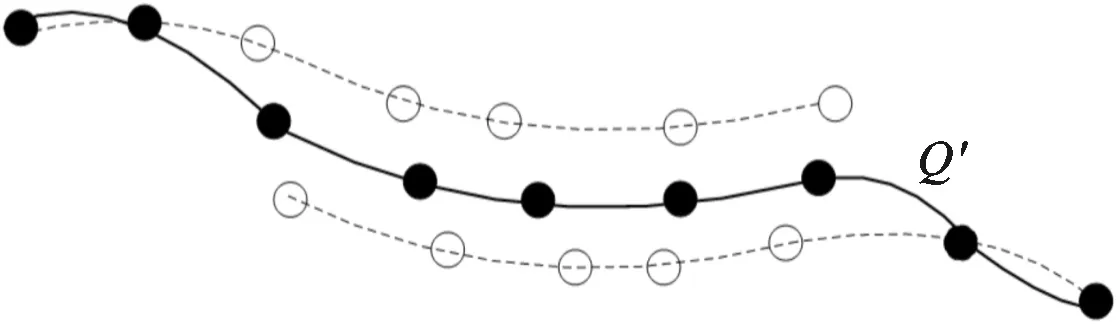
(b)模型扩展结果图4 模型扩展方法示意图

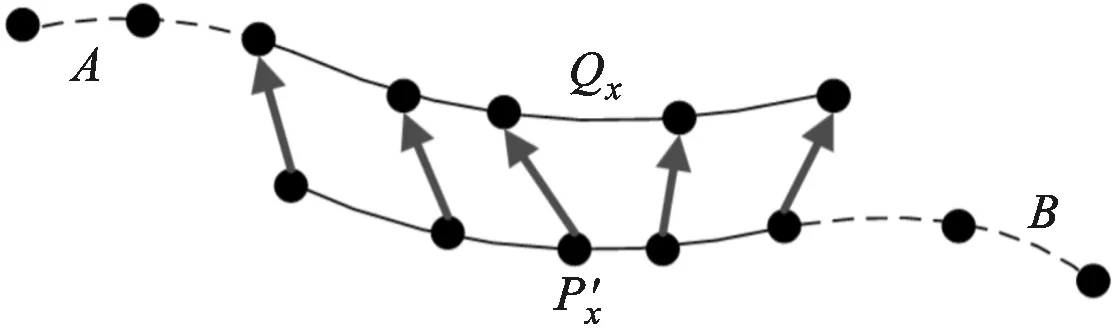
可将模型点云和变换后的数据点云分解为两部分

(9)

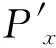
Q′=A∪F∪B

(10)

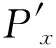
(11)

模型扩展时,对均匀采样所获得的特征同样需要进行扩展。本文所采用的特征包含特征点和特征描述两部分,其中特征描述分为法向量N和特征值差向量D两部分。在进行特征扩展时,可利用裁剪ICP算法建立重叠区域特征点的对应关系,并采用处理点云的方式确定新特征的特征点。由于特征值差向量具有旋转不变性,故新特征值差向量可由对应特征对的特征值差向量的均值所代替,即

(12)

而法向量不具有旋转不变形性,故在求平均法向量前,需要对数据点云中特征点的法向量进行旋转,然后再求平均

(13)

其中旋转矩阵R由双视角配准结果所确定。

与直接合并法相比,本文所设计的模型扩展法可有效地减少重叠区域的点云和特征的数目,从而有利于提高后续配准的效率。

2.4 多视角点云配准算法的实现

根据上述描述,结合图1的循环过程,可给出如下无序多视角点云全局配准方法。

步骤1从点云集里随机选出基准帧作为模型点云。

步骤2顺序遍历点云集的剩余点云,如点云集非空则转至步骤3;否则,转至步骤5。

步骤3视所遍历点云Pi为数据点云,利用2.1节中的方法计算(Ri,ti)和Ex,i。

步骤4根据式(7)判定(Ri,ti)的可靠性,如满足条件,转至步骤5;否则,转至步骤2。

步骤5从点云集里取出Pi,利用2.3节中的方法进行模型扩展,并更新平均值mE。

给定无序多视角点云集,利用本文方法可快速实现多视角点云配准。一般情况下,默认将点云集里的第一帧选为基准帧。

3 多视角点云配准实验结果

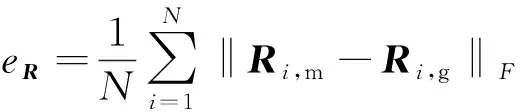
3.1 参数选取

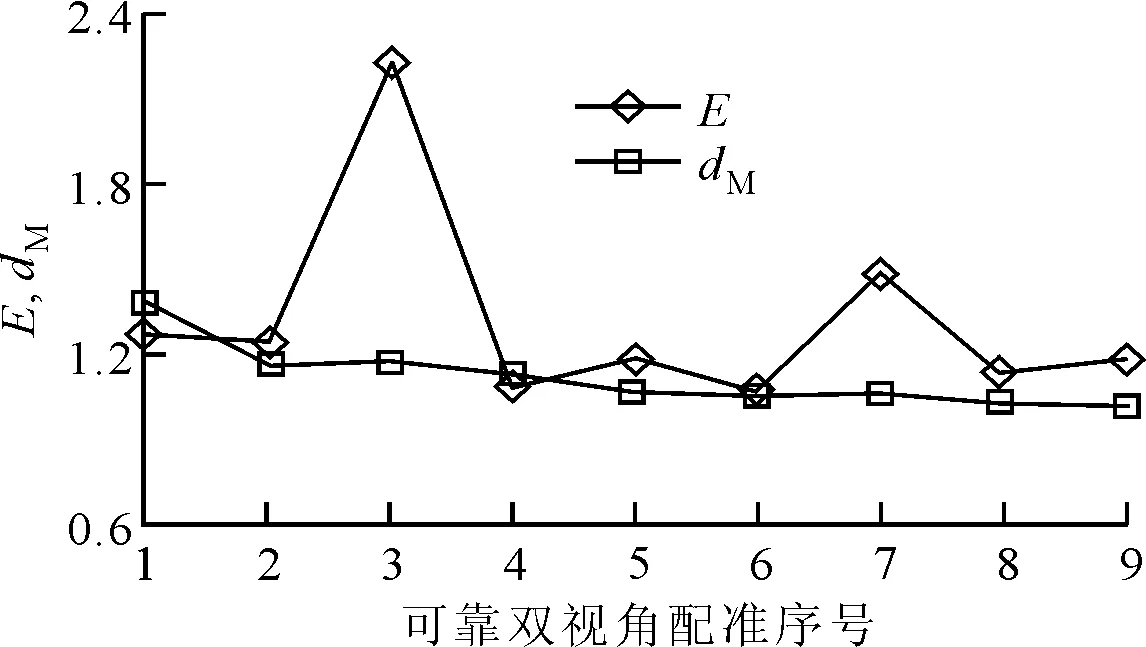
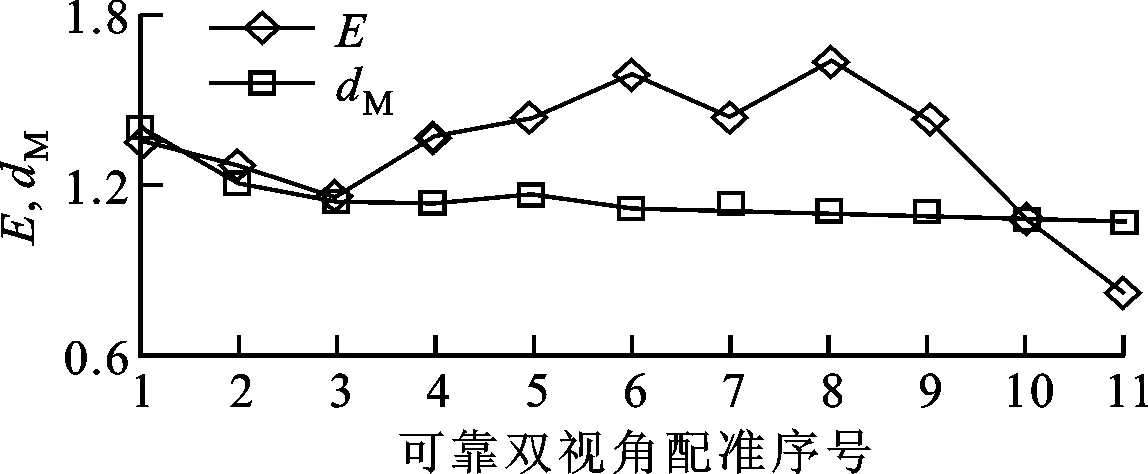
本文方法所包含的两个自由参数α和b的取值将影响本文方法的性能。为了选取合理的值,在Bunny和Armadillo数据集上对本文方法进行了测试,采用人工的方式挑选出了可靠的双视角配准结果,并在图5中记录了每次获得可靠双视角配准结果所对应的裁剪均方误差E和模型点云的平均密度dM。

(a)Bunny数据集

(b)Armadillo数据集图5 可靠双视角配准结果所对应的E和dM

如图5所示,对于可靠的双视角配准结果,点云密度dM一般小于裁剪均方误差E,且可靠双视角配准结果所对应的E波动比较大,为了确保配准结果判定准则的有效性,a和b的取值应该大于1。理论上,a和b越大越能确保挑选出全部可靠的双视角配准结果,但过大的a和b会引入不可靠的双视角配准结果,从而导致多视角点云配准结果的失败。通常情况下,不可靠的双视角点云配准结果是由低重叠百分比而导致的。如将a和b设置得较小,本文方法会将一部分点云的双视角配准结果误判为不可靠,但随着模型点云的不断扩展,待配准点云的重叠百分比将不断增加,前一次判定为配准失败的点云,下一次配准所获得的E将会变小,从而实现正确的判定,即较小的a和b仅降低了本文方法的效率,但较大的a和b值将降低本文方法的可靠性。鉴于此,可将参数a和b分别设置为a=2和b=1.5,以确保算法的可靠性。

3.2 配准算法的精度和效率

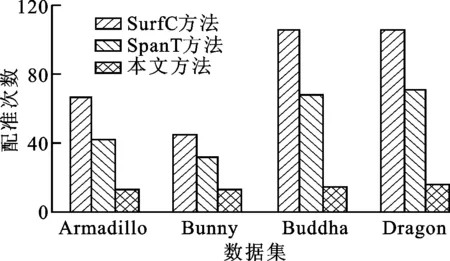
给定一组无序多视角点云,可以利用不同的多视角配准方法进行配准并进行性能对比。图6给出了不同方法在各个测试数据集上的效率对比结果,表1给出了不同方法在各个测试数据集上的精度对比结果,其中黑体数值代表最佳结果。为了进一步对比各种配准方法的精度,图7以横截面形式给出了各种方法关于Dragon和Buddha数据集的配准结果。

(a)双视角配准次数

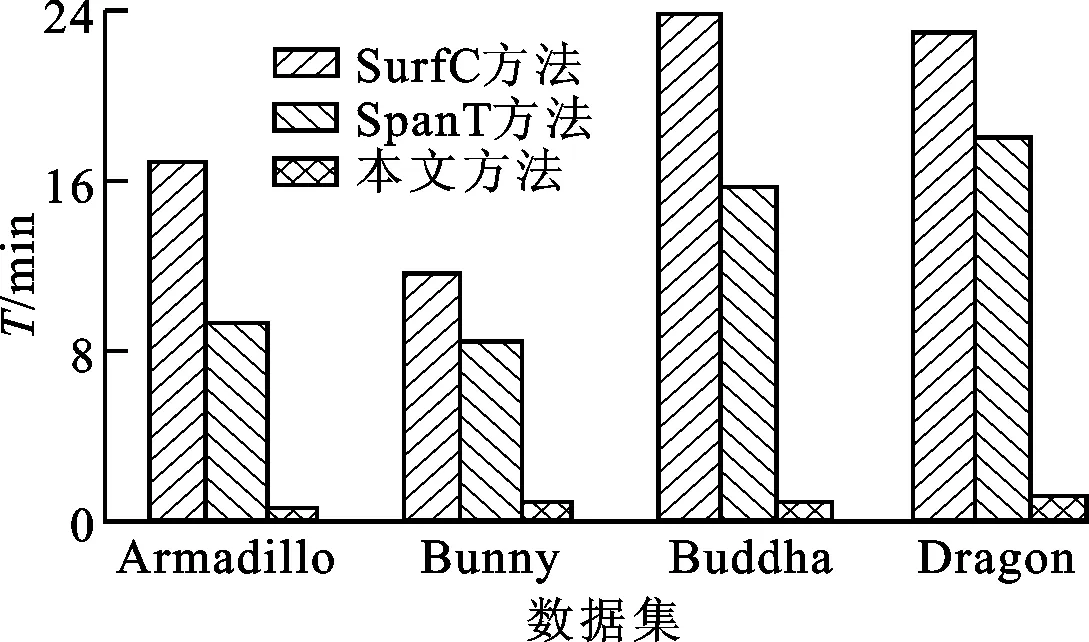
(b)程序运行时间图6 不同方法在4个测试数据集上的效率对比结果

由图6a可知,本文方法需要执行的双视角配准次数最少,算法效率最高;SurfC方法需要执行的双视角配准次数最多,算法效率最低。为了实现多视角全局配准,SurfC方法对点云集里所有的点云对进行双视角配准,并利用兼容性检测出可靠的双视角配准结果,以分析多视角配准结果。由于该方法需要执行双视角配准的次数最多,因此程序运行时间最长。SpanT方法采用深度优先的方式,通过执行双视角配准和寻找可靠的双视角配准结果创建完整的生成树。通常,双视角点云的重叠百分比影响其配准结果的可靠性,高重叠百分比的点云更容易获得可靠的配准结果。

在无序多视角点云集里,只有一部分点云具有高重叠百分比。为了创建完整的生成树,SpanT方法需要执行的双视角配准的次数较多,算法的效率较差。除执行双视角配准和寻找可靠双视角配准结果之外,本文方法引入了模型点云扩展步骤,利用可靠双视角配准结果进行模型扩展,可扩大模型点云所覆盖的区域,增加待配准双视角点云的重叠百分比,以减少双视角点云配准的执行次数,因此本文方法具有较高的效率。

由表1可知,本文方法配准精度最高,另外两种方法的精度较低。由于3种方法都采用双视角配准方法实现多视角配准,故均面临累积误差问题。其中SpanT和SurfC方法直接利用点云集里的原始点云对进行配准,通过不同的策略选取N-1组可靠的双视角配准结果计算多视角配准参数。通常情况下,双视角配准结果的精度受双视角点云重叠百分比的影响,且重叠百分比越低,配准精度越差。在多视角点云集中,许多原始点云对之间的重叠区域较少,对应的双视角配准结果精度有限,随着点云数的增加,多视角配准结果的累计误差将不断增大,从而导致SpanT和SurfC方法配准结果的精度变低。虽然本文方法也利用双视角配准结果实现多视角配准,但待配准的模型点云并不是点云集里的原始点云,而是不断扩展的点云。与原始点云相比,扩展后的模型点云可增加待配准的双视角点云重叠百分比,提高双视角配准结果的精度,从而减少多视角配准结果的累积误差,因此本文方法可获得最高精度的多视角配准结果。

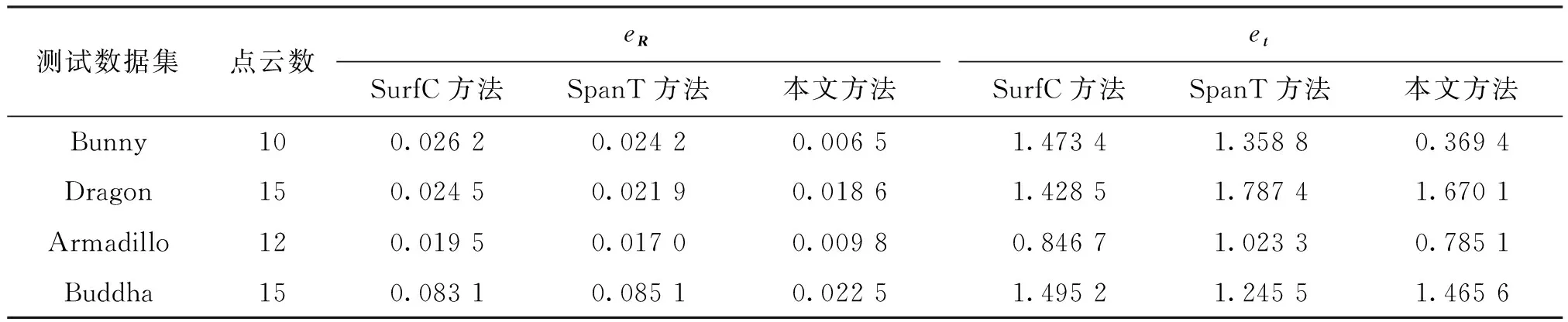
表1 不同方法在各个测试数据集上的误差对比结果

(a)输入数据(b)重建模型(c)SurfC方法(d)SpanT方法(e)本文方法图7 以横截面形式表示的配准结果对比

3.3 配准算法的鲁棒性

以Bunny数据集为实验对象,通过调整点云顺序测试所本文提出的多视角配准方法的可靠性,并与另外两种方法进行对比。表2给出了不同顺序下的Bunny数据集的配准结果。由表2可知,3种多视角配准方法对于点云的顺序都不敏感,即具有较好的可靠性。为了实现多视角配准,3种方法都设计了相应的准则,以确定可靠的双视角配准结果计算多视角配准参数。即使调整了点云顺序,这些方法仍可以选出可靠的双视角配准结果以实现多视角配准。与其他两种方法相似,本文方法对点云顺序具有较好的可靠性,是最佳的结果。

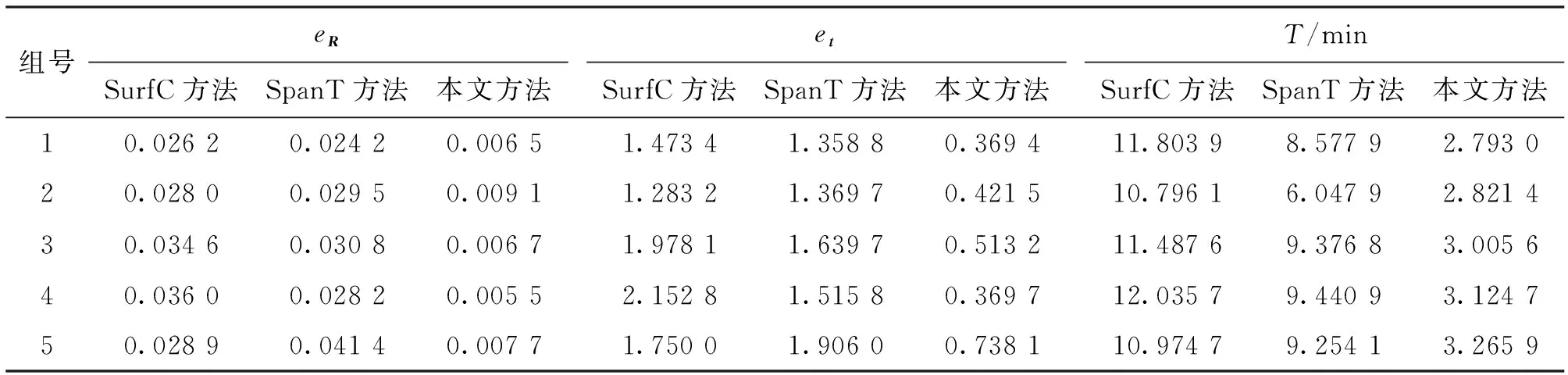
表2 不同方法关于Bunny数据集在不同顺序下的测试结果

4 结 论

针对无序多视角点云的配准问题,本文提出了基于特征匹配的全局配准方法,采用合理的特征描述算子实现双视角配准,并设计了判断双视角配准结果可靠性的准则,挑选出可靠的双视角配准结果,用于扩展模型点云。为实现多视角配准,该方法需要交替地执行双视角配准、配准结果判别和模型点云扩展,直到所有点云被扩展至模型点云。在斯坦福大学图形学实验室的公开数据集上的实验结果表明,与现有的多视角配准方法相比,本文方法具有较高的精度和效率。