核心素养视角下分式运算教学
2018-11-13黄雄
黄 雄
(厦门双十中学,福建 厦门 361000)
《义务教育数学课程标准(2011年版)》指出:运算能力是指根据法则和运算律正确地进行运算的能力。《普通高中数学课程标准(2017年版)》也将“数学运算”列入六大数学核心素养。运算能力实际上是运算技能与思维能力的结合,是数学核心素养关键能力之一。培养运算能力有利于学生理解运算的算理,寻求合理简洁的运算途径解决问题。
一、正确剖析数学概念是发展运算素养的基石
数学概念揭示了数学对象的本质属性,是数学运算法则导出的逻辑基础,是逐步形成运算技能、发展运算素养的基石。分式一章概念较多,其中分式与分数在结构上具有相似性,分式是两个整式的商(分母中的整式必须含有字母),分数是两个整数的商,都要求分母不为0。笔者在复习过程中穿插设计了以下四道例题:

设计意图:例1考查学生是否可以正确辨识分式;例2的目的在于正向引导学生巩固分式有意义的条件是分母不为0;例3则以逆向思维的方式,先指定字母x的取值范围,考虑所给选项中哪个分式可能没有意义;例4分式化简的结果是-x+3,学生极有可能任意取一数值代入计算求值,殊不知题干本身就隐含了x1±1,从而可能导致计算错误。
实际教学中,绝大部分学生都能正确解答例1与例2;而例3就有不少学生不知所措,究其原因是教师在日常教学时,大都按正向思维教学,平时学生的练习巩固题也几乎与例2相似,极少引导学生逆向思考。至于例4,在能够化简得到正确整式的学生中,有将近三分之一的学生没有选择0作为x的值代入求值,导致出错。当然也有部分学生将0代入求值,仅仅是因为计算简单,并没有深层次考虑到题干中字母x的限制条件。可见,死记硬背或仅从字面上强化数学概念,并不能真正引导学生理解掌握数学概念;只有坚持正向引导与逆向思维相结合,同时在复杂计算中不断巩固,方可让学生对数学概念的掌握内化于心、外化于形,为进行分式运算打好基础,从而促进运算素养的发展。
二、熟练运用性质和法则是提升运算素养的前提
从根本上说,运算是一种技能,运算技能需要依据运算法则和相关性质,在运算过程中按程序操作。因此学生必须明晰运算法则和相关性质,进行合理运算。不少学生初学分式约分时,经常会犯这样的错究其原因,就是对分式的基本性质掌握不扎实。我们知道,约分的依据是分式的基本性质:分式的分子与分母都乘(或除以)同一个不等于0的整式,分式的值不变。该性质可以用式子表示为:其中A,B,C是整式。有的学生将此性质简单理解为从而导致在计算本题时,直接将a和a2、b和b2进行约分,得出错误结论。因此,在分式运算复习课时,还是有必要设置相关辨析题。
[例5]下列等式从左到右的变形一定正确的是( )
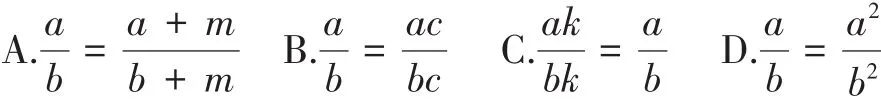
[例6]如果正数x、y同时扩大到原来的10倍,那么下列分式中,值保持不变的是( )
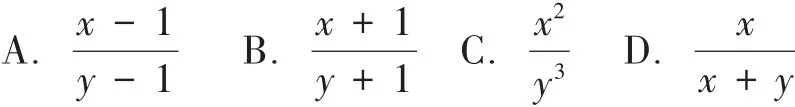
设计意图:例5中A和D两个选项,等式从左到右的变形都不是同时乘(或除以)同一不等于0的整式,容易排除。学生往往纠结于B与C选项,要选出正确答案,除了必须对分式概念的内涵与外延有准确的理解外,还要熟练掌握分式的基本性质。对于例6,在学生正确解答后,还可以适当引伸:当构成分式的分子和分母的整式中,各项次数均相等时,将各字母同时扩大(或缩小)n倍,分式的值不变。
实际教学以上两例时,尽管大部分学生都能得出正确答案,但耗费了不少时间。按教学设计之初的预想,笔者在实施教学过程中,大胆地对例6进行引申拓展。可学生的反应并不尽如人意,不得不放慢讲解速度,导致后续原定的教学任务只好做适当删减,留下些许遗憾。从这两个例子的教学效果来看,如果教师在实际教学中要求学生背默法则,以此来体现法则和性质的重要性,那是毫无益处的。问清错误,指出错因,重现过程,重新建构,才是指导学生熟练运用性质和法则的有效方法,提高数学运算素养的重要手段和途径。
三、领悟数学思想、理清算理是发展运算素养的核心
运算能力的培养与发展不仅反映在逐步提高运算技能方面,还应体现在提升和发展运算思维。在分式运算教学中,除了要学习和掌握分式运算方法,更应思考和领悟分式运算的算理和其中蕴含的数学思想。在反复练习、相互交流的过程中,教师要教会学生经常主动思考“为什么不能这样算?”“怎么算得好?”等问题。由法则到算理的顿悟过程,有助于学生领悟数学思想、理清算理,完成操作层面向思维层面的深层次建构,是数学运算素养发展的核心步骤。
由于分数与分式是特殊与一般的关系,对于分式而言,性质、法则基本上都是类比分数得来。因此,在分式运算教学过程中,应该充分利用数式通性,将学生学习分数的经验迁移到分式的学习中来,领悟其中渗透的类比、转化、化归等数学思想,达到事半功倍的

课后和学生交流中发现,犯此类错误的同学大都没有真正理解数式通性,分数运算能力比较薄弱,不能有效地迁移学习分数的经验。
众所周知,相关性质和法则是所有运算的基础。尽管因数分解在分数的乘除和加减运算中都起着重要作用,但功能不同。前者是为了找出分子分母相乘得出结果后的最大公因数约简分数,后者是为了找出各分母的最简公分母简化运算;两者都用到分数的基本性质,前者是为了约分约简分数,后者是为了通分转化成同分母分数的加减。
类比迁移:遇到分式相乘,迁移分数的乘法,分子分母各自相乘后约分即可;遇到分母是多项式的异分母分式相加减,先对各分母因式分解,找到最简公分母,然后通分转化为同分母分式的加减运算,接着依据同分母分式的加减法则操作,最后约简。一旦学生理清算理,领悟到其中隐含的数学思想方法,就不至于出现前文所述的困惑。
因此,在分式运算教学中,应通过例题和练习给学生方法上的指引,理解算理,领悟算法及其中蕴含的数学思想方法,正确迁移,才不会混淆或者错用法则。学生明晰了数学运算背后的算理,就明确了解题方向,才会采取自觉的行动,必将有助于学生运算能力的提升。
四、解决实际问题是提升运算素养的保障
分式与分式方程的复习安排两个课时,第二课时侧重于复习分式方程及其应用。在分式运算复习课教学中,仍须通过丰富的实际问题,渗透数学来源于生活,又服务于生活的教育理念,让学生充分体验建模思想。在实际问题教学中,教师要善于帮助学生从具体情境中抽象出数学问题,用符号语言表示数学模型,合理选择算法求解,这是提升运算素养的保障。
例8某工厂现在平均每天生产机器的工作效率是原计划的两倍,现在生产600台机器所需时间比原计划生产480机器所需时间节省了45天,原计划平均每天生产多少台机器?
对以上方程,学生可以选择不同解法。方法一,直接两边乘以2x去分母(通法);方法二:对于先再两边乘以x去分母;方法三,先约分,两边同时除以15,化成得x=4。
一般地,根据实际问题列出的方程往往数据比较大。如何正确、合理、快速地进行计算,考量着学生诸如观察、决策、推理、逻辑思维等多种能力。学生对算法多样性的选择需要在解题前养成观察的习惯,而在其中所体现的即是学生个体的数学素养,这需要学生有一定的解题经验和积累才能达到。
学生的数学运算能力是数学核心素养关键能力之一,良好的运算能力有助于学生数学核心素养的培养。在实际教学过程中,要想提高学生的数学运算能力,教师在教学中必须努力引导学生正确剖析数学概念,加强性质和法则的熟练应用;要帮助学生理解算理本质、领悟数学思想,重视联系生活实际,最终提升和发展学生的运算思维;要真正让学生养成会用数学的眼光看待世界,会用数学的思维思考世界,会用数学的语言表达世界;要提高学生学习数学的兴趣,促进学生运算能力的提升,从而培养学生数学核心素养。
