面向节能高效需求的数控加工系统多目标优化模型
2018-11-13江志刚
鄢 威 张 华 江志刚 马 峰
1.武汉科技大学服务科学与工程研究中心,武汉,4300812.武汉科技大学绿色制造工程研究院,武汉,4300813.武汉科技大学冶金装备及控制教育部重点实验室,武汉,4300814.武汉科技大学机械传动与制造工程湖北省重点实验室,武汉,430081
0 引言
随着全球变暖和环境恶化问题的日益严峻,以数控机床为能耗主体的数控加工系统能耗研究已引起大家的广泛关注[1-2]。减少数控加工系统能量消耗,提高能量效率,已成为现阶段制造业实现可持续发展亟待解决的科学问题。
数控加工系统能耗单元多且能量特性各异,其能耗呈现出复杂的动态特性,相关能耗建模与优化已成为国内外的研究热点。如BENNETT等[3]提出了一种基于Benders分解的数控加工系统能耗优化方法。KURAM等[4]建立了以比能量、刀具寿命和表面粗糙度为目标,以切削速度、切削深度和进给速率为变量的数控加工系统参数优化模型。ROZMARINA等[5]提出了一种基于遗传算法的刀具路径优化方法,可以在保证加工效率的同时减少数控加工系统能耗。SUBRAMANIAN等[6]建立了平面铣削过程能耗模型,并利用遗传算法进行了求解。LIN等[7]建立了综合考虑能耗和加工时间的数控加工过程多目标优化模型,并利用基于自适应教学学习算法对最优工艺参数进行了求解。YAN等[8]建立了以切削能耗、切削效率、表面加工质量为目标,以铣削工艺参数为变量的数控加工系统多目标优化模型。MA等[9]以数控铣削加工过程为研究对象,构建铣削加工过程能耗和时间多目标优化模型,利用遗传算法求得数控加工系统能耗最小的加工参数。LI等[10]通过大量实验拟合切削速度、切削深度与数控机床能耗间的函数关系,提出了通过调节工艺参数来实现机床节能的方法。李聪波等[11]构建了面向高效低碳的数控加工系统工艺参数和工艺路线多目标优化模型。伍晓榕等[12]基于DEMATEL-VIKOR理论,给出了绿色加工工艺参数的决策。陈行政等[13]以多工步数控铣削为研究对象,建立了以能效、加工成本为目标,以主轴转速、每齿进给量、背吃刀量、铣削宽度和工步数为变量的多工步数控平面铣削工艺参数多目标优化模型,利用自适应网格多目标粒子群算法进行求解。
本文从构成数控加工系统的各类耗能部件工作状态角度出发,构建反映其能耗动态特性的模型,并对节能高效优化方法展开研究。
1 数控加工系统能耗特性分析
数控加工系统耗能主体为各类数控机床,而数控机床又由主传动系统、进给系统等能耗单元组成。由于能耗单元的能量需求主要取决于其工作状态[14],在加工过程中,能耗单元的工作状态随加工进程变化而变化,故而数控加工系统能耗呈现出复杂的动态变化。
依据WD 14955-1[15]中机床构成部件功率特性分析,以及文献[16]中机械加工系统组成单元的分类,将数控加工系统能耗部件概括为时变能耗单元和非时变能耗单元。其中,时变能耗单元代表激活后工作状态随加工过程而变化的部件,如主传动系统、进给系统等;非时变能耗单元代表激活后工作状态基本保持不变的部件,如机床照明灯、显示屏等。
非时变能耗单元的工作状态包括启动、运行和停止,能耗主要发生在运行状态,近似等于额定功率与持续时间乘积,即
EOi=POitOi
(1)
式中,EOi为第i个非时变能耗单元Oi的能耗;POi为额定功率;tOi为运行工作状态持续时间。
时变能耗单元的工作状态包括启动、准备(包括加速和减速)、空载、负载和停止,能耗主要发生在空载和负载工作状态。对于启动和准备工作状态,有文献[17]认为虽其持续时间短,但这两个状态能耗峰值大且在加工过程中出现频次高,能耗不能忽略。
以能耗占比最高的数控加工系统主传动系统时变能耗单元为例,对其启动、准备、空载和负载工作状态的能耗特性进行分析。
主传动系统稳态功率平衡方程如下[18]:
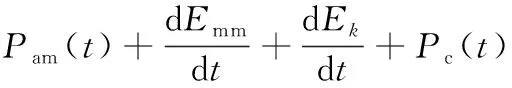
(2)
式中,Pin(t)为主传动系统输入功率;Ple(t)为电动机电损功率(包括电动机铜耗、铁耗、附加损耗和机械损耗等);Pum(t)为机械传动系统非载荷损耗功率;Pam(t)为机械传动系统载荷损耗功率;dEmm/dt为电磁场贮能的变化率;dEk/dt为主传动系统的动能变化率;Pc(t)为切削功率。
1.1 空载和负载工作状态
空载和负载工作状态均对应着主传动电机的稳态过程,区别在于是否产生切削功率Pc(t)。主传动系统空载和负载状态的能耗模型分别如下[19]:
(3)
(4)
1.2 准备工作状态
对应着主传动电动机暂态过程,准备工作状态的特征是切削功率和机械传动系统载荷损耗功率为零,电磁场储能变化、主传动系统的动能变化均不为零,且由于此状态下流过主传动电动机的电流很大,电动机铜耗不能忽略。
目前对主传动系统准备工作状态能耗建模通常是基于实验数据拟合的,对设备具体型号依赖较大,适用范围有限。本文结合主传动电机的电气性能入手,重点对功率平衡方程中电磁场贮能、动能、电动机电损等进行推导,进而推导出时变能耗单元准备工作状态通用能耗模型。
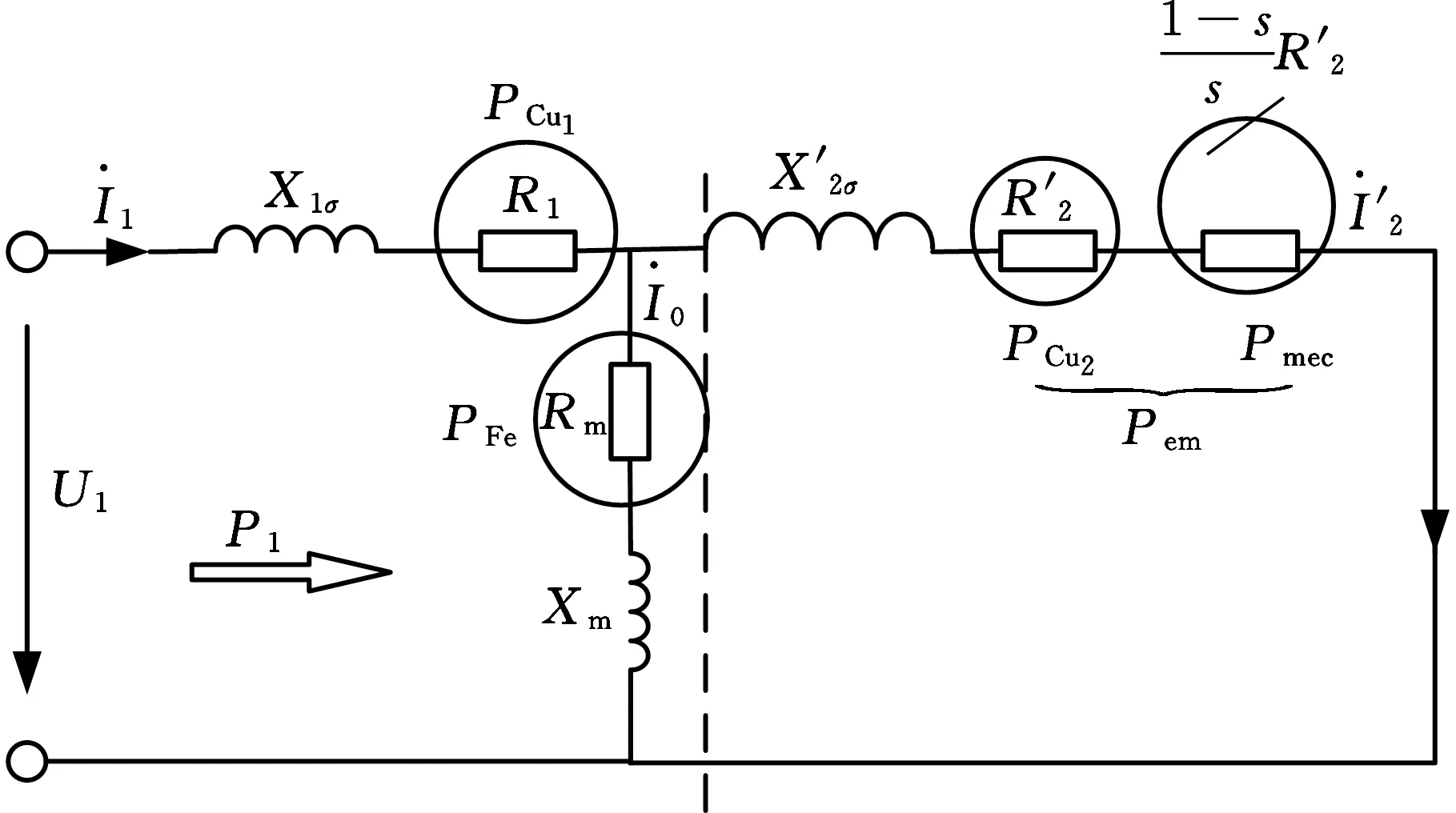
图1 异步电动机T形等效电路图Fig.1 T shape equivalent circuit diagram of asynchronous motor
设异步电动机同步转速为n1,则其与机械转速之间存在函数关系n=(1-s)n1。设电动机转子的机械角速度为ω,则有
基于图1可推导异步电动机稳态时的电磁转矩如下:
(5)
式中,Tem为异步电动机电磁转矩;P1为电动机电源侧输入功率;PCu1为电动机定子铜耗;PFe为定子铁耗;PCu2为转子铜耗;Pem为电磁功率。
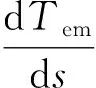
可求得该异步电动机最大电磁转矩和此时的转差率如下:
(6)
式中,Tm为异步电动机最大电磁转矩;m1为异步电动机定子相数;f1为电源频率;p为异步电动机的极对数;sm为在电动机最大电磁转矩时对应的电机转差率。
综合式(5)和式(6),建立最大电磁转矩Tm与电磁转矩Tem间函数关系如下:
(7)
机床主传动系统一般采用异步电动机拖动机械传动部件的驱动方式,结合电机拖动运行方程,可对机床主传动系统准备工作状态下能耗进行分析如下。
(1)电动机电损。由于此状态下电动机定子和转子铁损远小于铜损,其能量损耗近似等于铜损,即
(8)
式中,ΔECu为准备状态中主传动电机铜损。
(2)电磁场贮能变化率。通过电动机电磁转矩和角速度的乘积求得
(9)
式中,G为飞轮重量;D为飞轮平均直径;GD2为旋转部件的飞轮矩,且与转动惯量J存在转换关系:J=GD2/4g;g为重力加速度。
(3)动能变化率。通过主传动系统转动部件的转动惯量和角速度进行计算,即
(10)
式中,ω1、ω2分别为主传动系统转动部件准备状态前和准备状态后的转动角速度;n1、n2分别为对应ω1和ω2的转速。
(4)持续时间。通过主传动电机转差率变化求得
(11)
式中,TM为异步电动机拖动系统机电时间常数,可查阅产品目录获取;s1、s2分别为准备状态中异步电动机转差率的起始值和终止值。
将式(8)~式(11)代入式(2),可以建立主传动系统时变能耗单元在准备工作状态的能耗模型:
(12)
1.3 启动工作状态
可将启动工作状态看作准备工作状态中加速的一个特例,其特征是电动机初始转速n1=0,初始转差率s1=1,状态终结时转速达到规定转速n2,终止转差率s2=0。在工程实际中,一般认为s2=0.05时启动过程即已完成[21]。
结合式(12),数控机床主传动系统启动工作状态能耗分析模型可由下式表示:
(13)
基于式(1)、式(3)、式(4)、式(12)和式(13),即可通过不同能耗单元工作状态的能耗,建立数控加工系统动态能耗模型。
2 数控加工系统节能高效优化模型
2.1 优化变量确定
切削用量(切削速度vc、进给量f和切削深度ap)是影响数控加工系统能量消耗和加工效率的重要因素,为主要优化变量。ap一般可根据工件加工余量和具体加工要求来确定,可视为已知量;vc对加工过程能耗影响最大,进给量f则决定了加工时间和走刀时间,对数控加工系统能耗和效率的影响较大[11]。本文选择切削速度和进给量作为数控加工系统能效多目标优化模型的变量。
2.2 优化目标函数
2.2.1能耗目标函数
数控加工系统的总能耗为构成系统的所有时变和非时变能耗单元在加工过程中不同工作状态的能耗之和。由于数控加工通常用于多加工特征零部件,且每个工件加工特征均对应着一组能耗单元的工作状态变化情况,因此,可对每个加工特征下的能耗单元工作状态能耗进行加和,建立反映数控加工系统动态能耗过程的目标函数。设数控加工系统中包括m个非时变能耗单元和n个时变能耗单元,且加工工件具有k个加工特征,则其能耗目标函数可由下式表示:
(14)
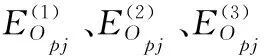
2.2.2加工时间目标函数
文中通过数控机床主传动系统在加工过程中启动、准备、空载和负载工作状态的持续时间来构建。
(1)启动和准备工作状态持续时间。由2.1节分析,数控加工系统启动和准备工作状态持续时间分别由下式表示:
(15)
(16)
(2)空载工作状态持续时间。主传动系统空载工作状态持续时间主要包括刀具和夹具更换时间。设刀具和夹具更换一次的时间分别为TT和TF,则数控加工系统空载工作状态持续时间可表示为
(17)
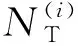
(18)
(3)负载工作状态持续时间。可由工件尺寸和切削速度等进行计算,即
(19)
式中,LT为刀具走刀路径长度;vT为刀具进给速度。
同能耗目标函数构建方法,设加工过程中有k个加工特征,则其加工时间可由k个特征加工中不同工作状态的持续时间累加进行计算。同时注意到启动工作状态并不是在每个特征加工中都会出现,本文对其进行单独计算。数控加工系统加工时间目标函数可由下式表示:
(20)
式中,TA为数控加工系统总运行时间;q为时变能耗单元启动工作状态的重复次数;s1i、s2i分别为异步电动机在第i个特征加工中对应的准备工作状态下初始转差率和终止转差率;LTi、vTi分别为第i个特征加工中对应的刀具走刀路径长度和刀具进给速度。
2.3 约束函数
为避免模型与实际工程应用相悖和防止优化结果难以保证加工质量的要求,对上述模型参数的约束关系进行分析。
(1)主轴转速约束。设数控机床允许的最小主轴转速为nmin,最大转速为nmax,则主轴转速约束可表示为:nmin≤n≤nmax,由于主轴转速可以表示为切削速度的函数,将主轴转速约束转换为切削速度变量的约束,即
(21)
式中,d为加工工件直径。
(2)进给量约束。数控加工过程中,进给量必须在机床允许的最小进给量fmin和最大进给量fmax之间,即:
fmin≤f≤fmax
(22)
(3)切削力约束。数控加工过程中,切削力不能超过机床所允许的最大切削力,即
(23)
式中,Fc为主切削力;CF、xF、yF、nF、KF为模型计算系数,可通过查阅机械工艺手册获取;Fmax为机床所能输出的最大切削力。
(4)切削功率约束。数控加工中,切削功率应小于机床所能提供的最大有效切削功率,即
(24)
式中,Pmax为机床所能提供最大切削功率;η为效率。
(5)刀具寿命约束。较高的主轴转速和进给量可以显著提高加工效率,但过大的切削速度和进给量可能造成刀具加工时的受力呈几何级增长,可能导致刀具使用寿命缩短,甚至刀具损坏,影响加工效率,因此,数控加工过程中参数选择必须满足刀具寿命的约束,即
(25)
式中,TTool为加工时的刀具寿命;d0为刀具直径;ae为切削宽度;z为刀具齿数;Cv、Kv、xv、yv、sv、qv、pv、l分别为刀具和工件材料的相关系数,可通过查阅切削用量手册来获取。
泰勒广义刀具耐用度函数T的计算式为
(26)
式中,CT为与加工条件有关的常数;x、y、z为刀具寿命系数。
(6)加工质量的约束。加工质量是优化的前提,无论采取何种优化,都必须要保证加工质量符合要求。加工表面质量是数控加工参数优化的一个重要约束,在本文中用表面粗糙度表示,即加工工件的表面粗糙度必须满足零件质量最低粗糙度的限定,即
(27)
式中,Ra为加工后的工件表面粗糙度;Ramax为表面粗糙度允许的最大值;θa为刀具前刀角;αa为刀具后刀角。
2.4 数控加工系统节能高效多目标优化模型
数控加工系统节能高效优化模型为一个典型的带约束多目标优化问题,表示如下:
minf(vc,f)=(minET,minTA)
s.t.
(28)
3 基于小生境遗传算法的模型求解
目前对带约束多目标优化问题最常用解法是遗传算法(genetic algorithm, GA),但该方法存在易收敛到局部最优,出现算法早熟现象的问题[22]。本文提出了一种基于小生境遗传算法 (niche genetic algorithm, NGA)的数控加工系统节能高效多目标优化求解方法,即是将个体小生境半径与切削速度和进给量变量共同参与染色体编码,同时利用遗传操作(选择、交叉和变异)进行迭代计算,在达到设定终止条件时解码最优个体,得到使得能耗和加工时间最小的优化结果和对应变量。该方法通过小生境半径编码和调节达到保证种群多样性,避免陷入局部最优的缺陷。
3.1 染色体编码
(1)染色体编码。选用自然数字链编码作为编码方式,包括决策变量和小生境半径两部分,个体编码串如下:
(29)
其中,xk∈[Mk,Nk]为目标函数的第k个决策变量,对应优化模型变量进给量和切削速度;σsh为小生境半径,其计算公式如下:
(30)
式中,m为小生境数,即该优化问题的最优解个数。
3.2 求解步骤
(1)小生境环境设置。设小生境遗传算法共享函数为sh(dij),个体xi小生境个数为mi,则共享函数和小生境个数可由下式表示:
(31)
(32)
其中,n为群体规模,mi为个体xi的小生境数,dij为种群中个体xi、xj的欧氏距离,由数控加工系统能耗和加工时间目标函数进行计算:
式中,fE(x)、fT(x)分别为数控加工系统能耗和加工时间的目标函数。
(2)遗传操作。
a.选择操作。利用式(30)~式(32)计算种群所有个体共享程度,并将个体xi适应度函数f(xi)调整为fsh(xi)=f(xi)/mi,以达到保证种群多样性、抑制相似个体无限增殖的目的。选择操作根据调整后个体的适应度值大小进行自适应调整,计算方法如下:
(33)
b.交叉操作。基于自适应非均匀交叉算子产生新的个体,计算方法如下:
(34)
α=exp(-a0t/T0)
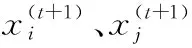
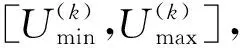
(35)
Δ(t,y)=y(1-r(1-t/T)b)
式中,Δ为变异步长;r为[0,1]范围内的随机数;b为系统参数。
数控加工系统节能高效优化模型的小生境遗传算法求解步骤如下。
(1)算法初始化。染色体编码,确定适应值函数,设定遗传参数,生成初始种群P0。
(2)完成个体适应度计算,并按降序排列。
(3)对前N个个体执行选择、交叉、变异等遗传操作。
(4)完成种群中所有个体共享度的计算。
(5)根据个体的共享度,对每个个体的适应度重新进行计算。
(6)比较子代和父代个体适应度大小。
(7)用适应度大的子代个体替换父代个体,形成新一代种群。如果由于交叉或变异算子改变基因值导致某个个体峰半径基因全部为0,则随机选取其中一个基因,并将其值置为1。
(8)若满足收敛条件,则算法终止;否则返回步骤(2)。
NGA算法流程如图2所示。

图2 小生境遗传算法流程Fig.2 The flow chart of NGA
4 案例分析
4.1 实验条件
以某机床中心架底座平面和通槽加工为案例对上述模型和算法进行验证。该工件包括6个平面(a~f)和1个通槽(g)的加工,其中,平面a、b、e和f需1次进刀,平面c、d需要2次进刀,通槽g需要6次进刀。利用数控铣床XK713进行加工,其加工信息如表1所示。
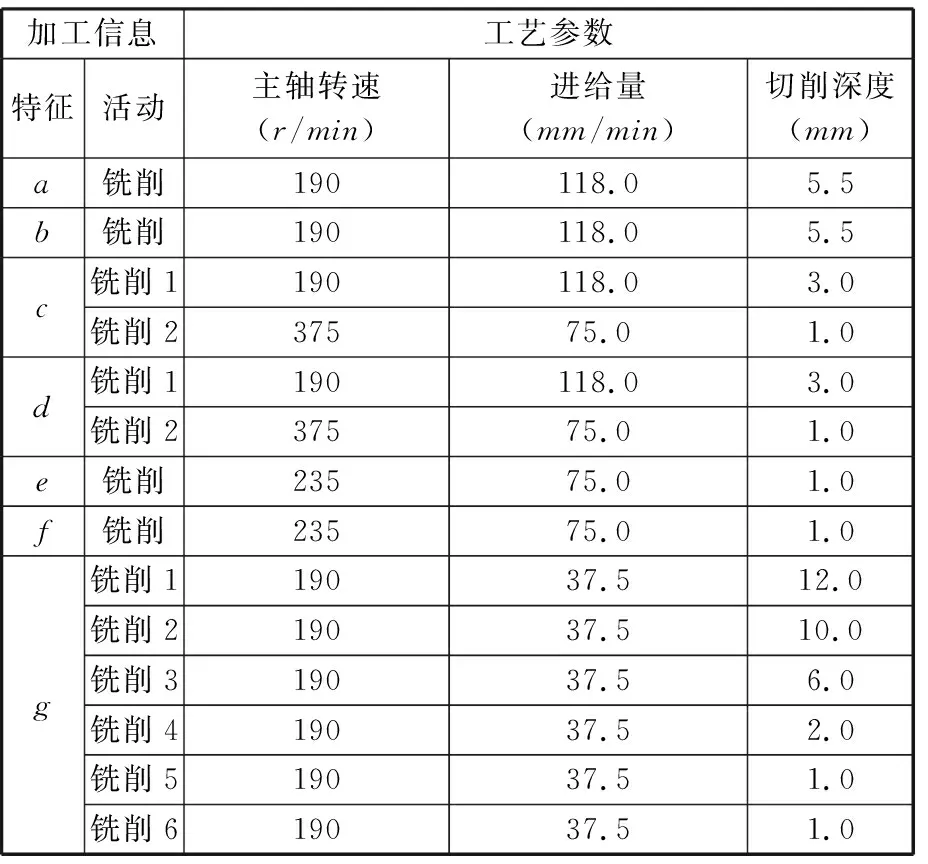
表1 加工信息和参数
依据前文分析,构建数控加工系统节能高效多目标优化模型,相关主要参数如表2所示。
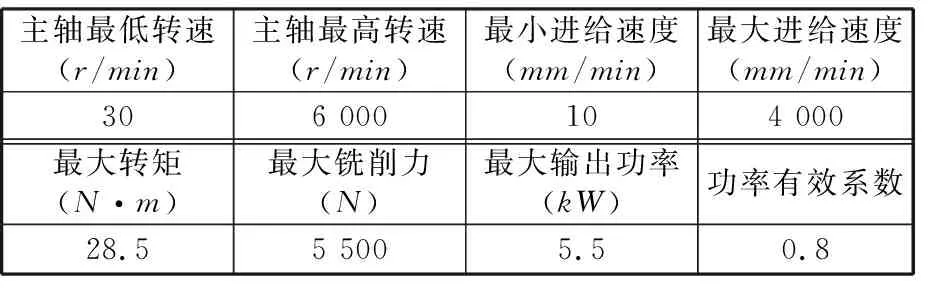
表2 铣床XK713规格参数
4.2 模型求解与结果分析
4.2.1优化模型求解
由于该中心架底座的平面a、b、e和f,以及通槽g的第5和第6次加工所采用的加工方案和参数相同,为简化求解过程,在本文中将这几组加工视为一个工艺活动,对该数控加工系统的10组工艺活动分别进行优化。将表1~表2参数代入数控加工系统节能高效多目标优化模型,利用MATLAB2013b编写小生境遗传算法程序进行求解,并设置种群大小为50,最大迭代次数为500,交叉概率为0.8,变异概率为0.1。
优化结果以及在能耗和加工时间目标分别最优时对应的工艺参数如表3所示。由表3可以看出切削速度和进给量均是数控加工系统能耗和加工时间的重要影响因素,且数控加工系统的能耗与切削速度和进给量正相关,加工时间与切削速度和进给量负相关。如工艺活动2中数控加工系统能耗和加工时间随切削速度和进给量的变化趋势分别如图3所示。
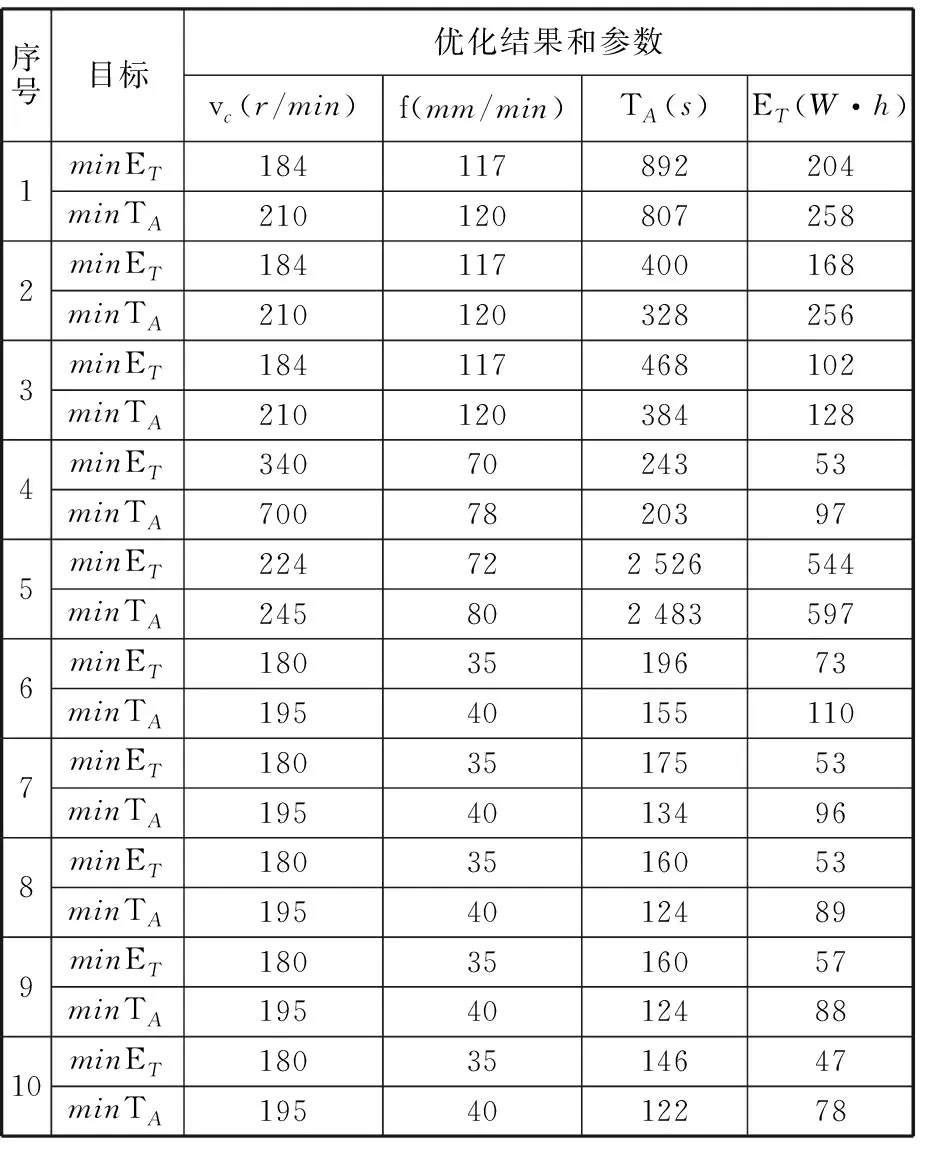
表3 优化结果及对应参数
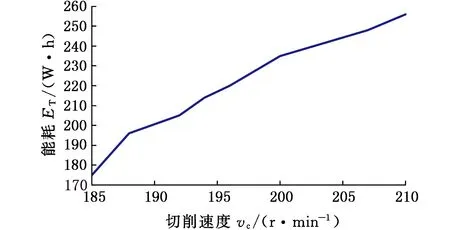
(a)vc与ET的关系曲线
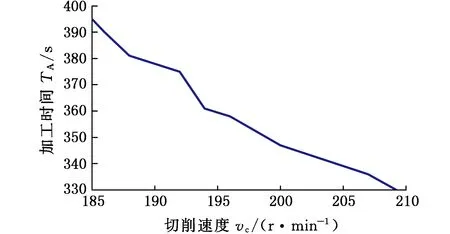
(b)vc与TA的关系曲线
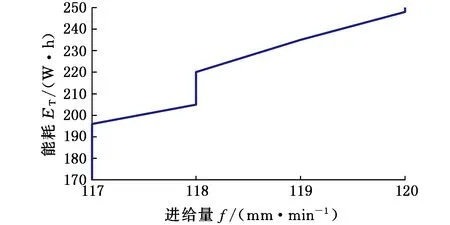
(c)f与ET的关系曲线
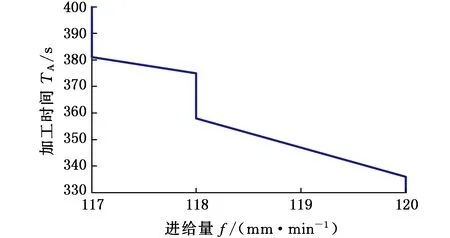
(d)f与TA的关系曲线图3 能耗、时间随切削速度、进给量变化趋势Fig.3 Trend of energy consumption and time with cutting speed and feed rate
4.2.2优化结果分析
为对求解结果和算法性能进行说明,本文将NGA优化结果与实际测量结果,以及分别用NGA与GA优化求解的结果进行了对比。
4.2.2.1 优化结果与实测结果对比分析
利用横河高精度功率测量仪WT1800对该数控机床能耗和加工时间进行测量。
将优化结果与实测结果进行对比,从单工艺活动和整体两个层面对优化结果进行了对比分析。
(1)单工艺活动优化结果对比。通过调节切削速度和进给量可以有效减少数控加工系统的能耗和加工时间。以每个工艺活动中最优能耗时能耗相对实测数据减少的百分比,以及时间最优时加工时间相对实测数据减少的百分比进行说明,如表4所示。从表4可以看出,通过调节加工参数,最大可以减少工艺活动27.92%的能量消耗(工艺活动8)和减少工艺活动23.43%的加工时间(工艺活动7)。该结果说明了调节工艺参数是减少数控加工系统能耗、提升能效的有效手段。该优化结果及对应的参数可为工艺人员提供决策选择依据,在实际加工中达到提升数控加工系统能效的目的。
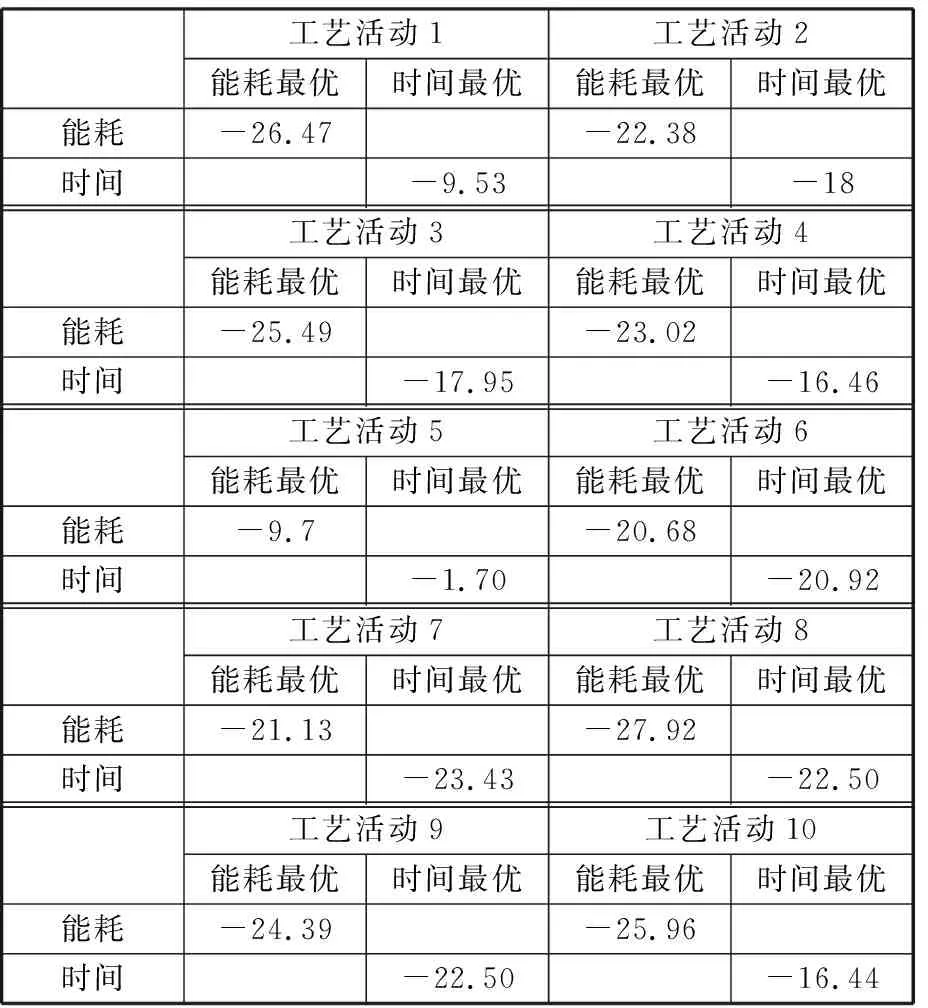
表4 单工艺活动优化结果与实测结果对比分析
(2)整体优化结果对比。将使得每个工艺活动中能耗最优对应参数以及加工时间最优对应的参数分别作为该中心架底座加工参数进行加工,整个加工过程的能耗和加工时间优化结果与测量结果的对比分析如表5所示。

表5 优化结果与测量结果对比分析
由表5可以看出,通过切削参数优化,在能耗最优目标下可实现数控加工系统总能耗减少2.37%;在时间最优目标下可实现数控加工系统总加工时间缩短3.45%,说明了本文算法的有效性。
在实际应用中,企业可以根据实际需求,选择相应的优化参数,以达到能耗和效率的协同优化。
4.2.2.2 小生境遗传算法与遗传算法对比分析
为说明本文所提算法的优越性,利用遗传算法对该多目标优化问题进行了求解。如以工艺活动2为例对两种算法性能进行分析,该工艺活动中两种算法的优化结果分别如图4所示。
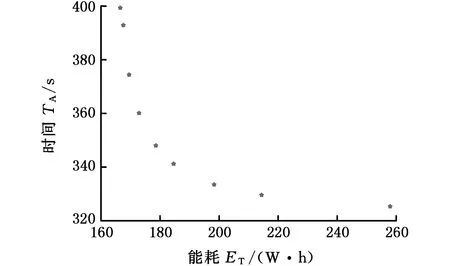
(a)NGA优化结果分布

(b) GA优化结果分布图4 NGA与GA算法计算结果对比Fig.4 Comparison with NGA and GA algorithm
由图4可以看出,NGA的优化解个数多于GA的优化解个数,且解在Pareto前沿面分布更为均匀,说明了本算法能较好地保持种群的多样性,具备更好的全局搜索能力,验证了本文所提算法的有效性与优越性。
5 结论
(1)从能耗单元工作状态的角度对数控加工系统能耗进行分析,构建了反映其多源动态能耗特性的能耗模型。
(2)建立以切削速度和进给量为变量,以最小能耗和最短加工时间为优化目标,设备性能、加工质量等为约束的数控加工系统节能高效多目标优化模型。
(3)针对遗传算法容易陷入局部最优的问题,提出一种基于小生境遗传算法的数控加工系统节能高效多目标优化模型求解方法。
(4)通过实际案例对优化结果及算法性能进行对比分析,结果表明:本文所建模型和方法可有效减少数控加工系统的能耗和缩短加工时间,为数控加工系统能效的提升提供方法支撑;本文提出的NGA算法相比于GA算法,在较好保持种群多样性的同时具备更好的搜索能力和收敛速度,避免了求解过程中陷入局部最优而造成全局最优解遗失的问题。
