基于零件结构耦合关系的主动再制造设计方法

宋守许 汪 伟 柯庆镝 邱 权

合肥工业大学机械工程学院，合肥，230009

0 引言

《中国制造2025》和 “十三五”规划中均提出要大力发展再制造产业，国内外学者对此开展了相关研究。姚巨坤等[1]针对再制造的产品材料设计、结构设计、生产设计等内容进行了研究；SUNDIN等[2]对如何优化再制造产品设计过程进行了研究，以提高再制造的效率；LIU等[3]针对再制造加工系统可持续性评价的不足，提出了一种新的基于能值的再制造加工系统的评价方法。

不同于国外的“换件法”再制造策略，我国再制造策略主要采用“尺寸恢复法”，该策略的产业化瓶颈主要是再制造毛坯质量和数量的不确定性，为此提出了主动再制造的概念。主动再制造是将产品全生命周期纳入设计阶段，在最佳时间段内对产品实施再制造的过程，而主动再制造设计是实现主动再制造的有效手段。人们对主动再制造的研究尚处于起步阶段。宋守许等[4-5]分别从产品、零件和结构层面对主动再制造设计进行了研究，提出了主动再制造设计理论与设计方法，同时提出了寿命匹配的概念及其优化设计方法。

目前由于结构间存在复杂的耦合关系，对零件某一特征结构的优化易导致其他结构的劣化，进而导致零件整体性能降低。为解决上述问题，本文在对零部件结构耦合规律研究的基础上，提出了相应的主动再制造设计方法。

1 零件结构耦合关系

在机械设计过程中，零件结构具有机械特性，零件某一结构的特征参数变化不仅对自身性能产生作用，还可能会影响其他结构的性能，则称该影响关系为机械零部件的结构耦合关系。由于对某一特征结构或某一结构参数进行研究难以揭示结构间的耦合作用规律，故本文将零件视为一个有机整体，研究构成整体各要素间的耦合作用规律，并提出结构功能耦合系统的概念。

1.1 结构功能耦合系统

结构功能耦合系统是将零件视为一个有内部相互作用关系的有机整体，在分析零件结构间的机械特性和力学关系的基础上，运用方差分析和函数拟合的方法量化结构间的耦合关系，以直观地展现零件结构间耦合作用规律的逻辑框图。

结构功能耦合系统由零件结构间耦合关系、结构影响因子、结构强度关于设计参数及参数间交互作用的映射函数三部分组成。建立零件结构功能耦合系统模型的步骤如下：①根据零件机械特性判断结构间可能存在的耦合关系；②设计具有交互作用的正交试验，并对试验数据进行方差分析，得到设计参数及参数间交互作用对各结构冗余强度[6]的影响程度；③选择对结构冗余强度影响较大的设计参数和参数间的交互作用，在MATLAB中进行函数拟合，得到结构强度关于设计参数及参数间交互作用的映射函数；④在上述所有工作的基础上，用系统思维搭建描述零件结构间耦合作用规律的逻辑框图(即零件结构功能耦合系统模型)。

结构功能耦合系统揭示了零件结构耦合关系，量化了耦合作用规律，可由此判断参数变化时引起的零件其他结构的性能变化。同时，为量化设计参数变化对各结构冗余强度的影响，本文提出了结构影响因子的概念。

1.2 结构影响因子

结构影响因子的定义及求解过程如下：通过失效统计和设计经验，可以获取零件的薄弱结构(S1，S2，…)，及可能对薄弱结构S1冗余强度有影响的设计参数xp(p=1,2,…,m)，可能对薄弱结构S2冗余强度有影响的设计参数xq(q=m+1,m+2,…,m+k)，根据实际情况选择合适的表头，设计具有交互作用的正交试验，以获取不同设计参数及参数交互作用水平组合下的各结构冗余强度。

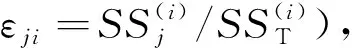
1.3 结构功能耦合系统模型建立

以发动机曲轴为例来说明结构功能耦合系统模型的建立过程。曲轴在实际应用过程中的主要损坏原因是疲劳和磨损，目前再制造技术已可实现对曲轴磨损的完全修复，故本文只考虑曲轴的疲劳强度，主轴颈、连杆轴颈、主轴颈圆角、连杆轴颈圆角、曲柄臂、油孔和平衡块等是曲轴主要的特征结构。

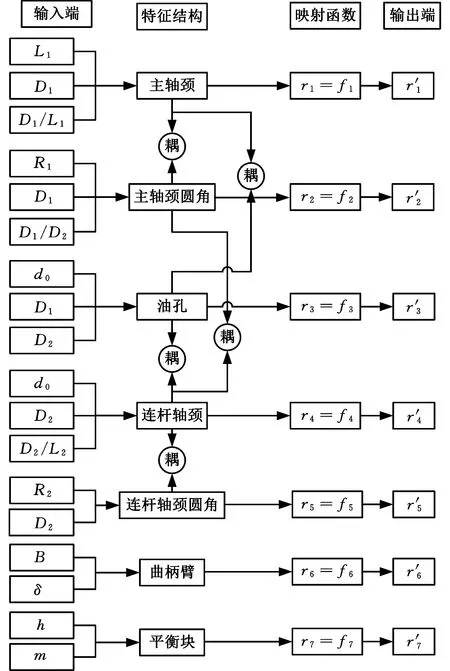
图1 结构功能耦合系统模型Fig.1 Function coupling system model of structure

2 基于零件结构耦合关系的设计方法

通过上述研究可建立零件结构功能耦合系统模型，揭示零件结构间的耦合关系，但优化某一结构而导致另一结构劣化的问题仍未解决，因此本文提出了基于零件结构耦合关系的主动再制造设计方法。采用结构功能衍生系数优化法[9]进行优化设计，在确定结构冗余强度关于设计参数及设计参数间交互作用映射函数的基础上，建立衍生系数导数矩阵(derivative coefficient matrix,DCM)和单调性矩阵，进而得到结构冗余强度对设计参数的单调性关系，并由此对参数进行优化设计。整个优化流程可分为以下3个步骤：

(1)结构耦合关系分析。将零件视为一个有内部相互作用关系的有机整体，分析具体零件的机械特性及其服役时各结构间的力学关系，判断零件结构间可能存在的耦合关系。

(2)设计试验及数据处理。根据零件结构及设计参数间可能存在的耦合作用，设计具有交互作用的正交试验。对试验结果进行方差分析并计算结构影响因子，以量化设计参数对结构冗余强度的影响程度。选择结构影响因子较大的设计参数和参数间的交互作用，运用MATLAB进行函数拟合，得到结构冗余强度与设计参数及其交互作用的映射函数，并建立结构功能耦合系统模型。

(3)优化设计。根据所得函数模型，将不满足冗余强度条件(冗余强度条件为r≥1.25)的结构作为优化对象，采用结构功能衍生系数优化法对设计参数进行优化，最终使零件满足冗余强度条件或数据处于设计范围内。

3 实例分析

以6L240型号柴油机曲轴为例，以曲轴易发生疲劳损坏的结构主轴颈、连杆轴颈、轴颈圆角和油孔为研究对象，并建立其结构功能耦合系统模型，见图1。以主轴颈直径D1、连杆轴颈直径D2、主轴颈圆角半径R1、油孔直径d0和连杆轴颈长度L2为优化对象，根据设计手册，得到各结构设计参数的取值范围，见表1。

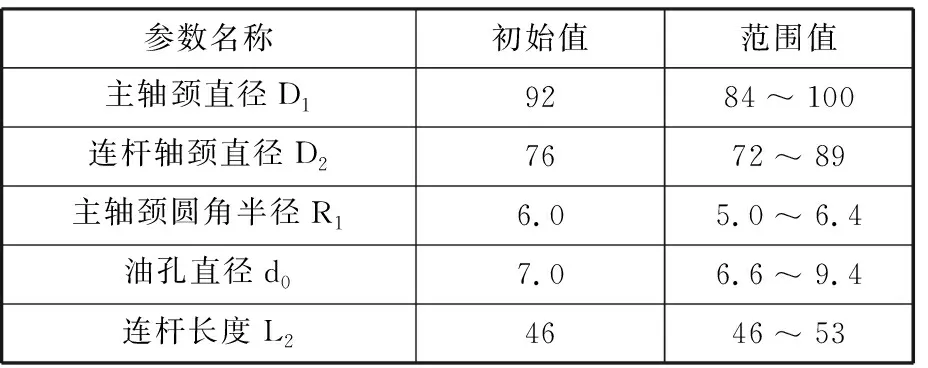
表1 结构设计参数的范围

采用ABAQUS软件对曲轴进行应力分析，并采用Fe-safe软件对曲轴进行疲劳分析以得到其寿命云图见图2，用应力循环次数表征曲轴的疲劳寿命，图中的数值大小表示应力循环次数的常用对数值(lgn)。由图2可以看出，仿真过程中该曲轴的最小疲劳寿命值为n=108.778次(即应力循环次数为108.778)，出现在主轴颈圆角处，且连杆轴颈同样为薄弱部位。

图2 曲轴疲劳寿命仿真Fig.2 Fatigue life simulation of crankshaft

根据该柴油机的使用工况[10](使用寿命为30年，每年工作365 d，每天20 h，曲轴1 000 r/min)，推测其寿命周期内的应力循环次数为n= 6.7×109(曲轴在一个寿命周期内所损耗的疲劳寿命为6.7×109次)。

结合冗余强度的计算公式，由于现有技术对零件疲劳损伤的恢复效果甚微，可认为强度恢复量H≈0，故曲轴的冗余强度为

i=1,2,…,I

式中，Di为零件结构Si在设计阶段的最大强度允许损伤量；Di(t)为经过t时间的服役后，结构产生的强度损伤量；Hi(t)为结构Si在t时刻进行再制造可恢复的强度量；Ni为结构Si在当前载荷水平下的疲劳寿命。

本文采用具有交互作用的正交试验法进行分析，仅考虑因素间的一级交互作用(两两交互作用)并将试验因素分为2个水平，分别见表2～表4。

表2 主轴颈圆角试验因素水平

表3 连杆轴颈试验因素水平

表4 油孔试验因素水平

根据图2，选取对主轴颈圆角、连杆轴颈和油孔有影响的设计参数作为试验因素，按L8(27)的正交试验表进行试验，并根据试验结果计算零件各薄弱结构在不同设计参数组合下的冗余强度，结果分别见表5～表7，其中，“×”表示交互作用,1和2表示交互作用的水平。

表5 主轴颈圆角的冗余强度r1的试验值

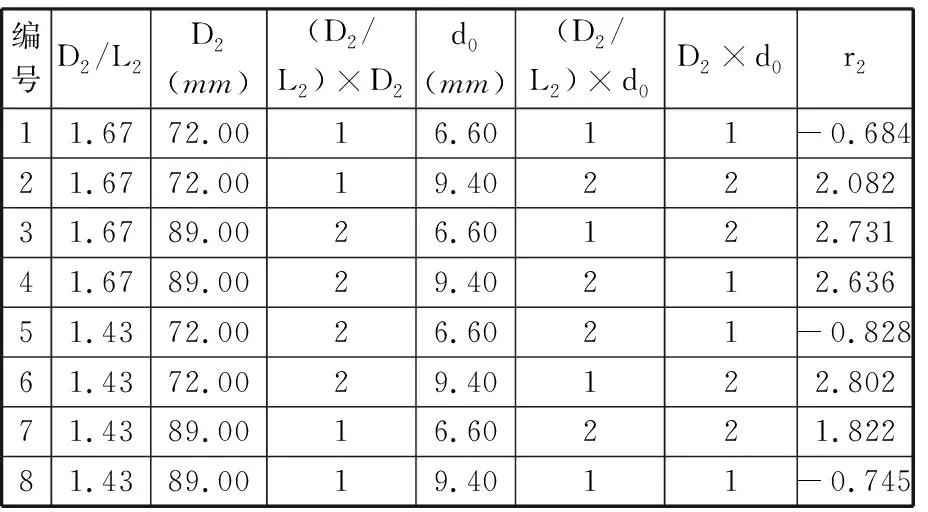
表6 连杆轴颈的冗余强度r2的试验值

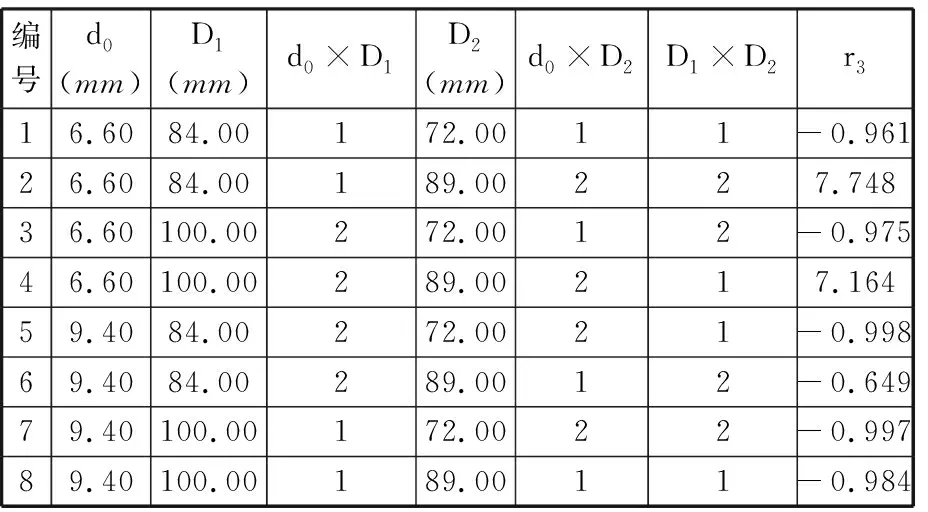
表7 油孔的冗余强度r3的试验值

对仿真试验结果进行方差分析，得到结构强度对设计参数的结构影响因子，分别见表8～表10，其中，E表示组内，T表示总体。若某一结构冗余强度对某一设计参数的结构影响因子小于5%，则表明该设计参数的变化对结构冗余强度的影响程度不大，故本文只对结构影响因子大于5%的设计参数进行优化设计。

根据方差分析结果可知：D1/D2、R1及其交互作用(D1/D2)×R1对主轴颈圆角疲劳强度的影响程度较大，D2/L2、D2、(D2/L2)×D2、d0和D2×d0对连杆轴颈疲劳强度的影响程度较大，d0、D2和d0×D2对油孔疲劳强度的影响程度较大。

将试验所得数据通过MATLAB，采用多元线性回归与响应面相结合的方法进行函数拟合。为防止拟合阶数过高而产生振荡，取拟合函数阶数为2。冗余强度r1、r2、r3的拟合函数分别为

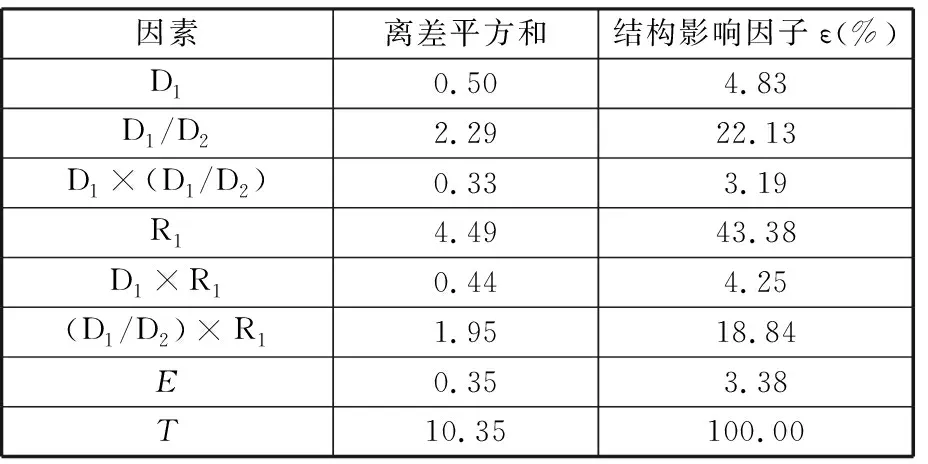
表8 主轴颈圆角冗余强度试验方差值

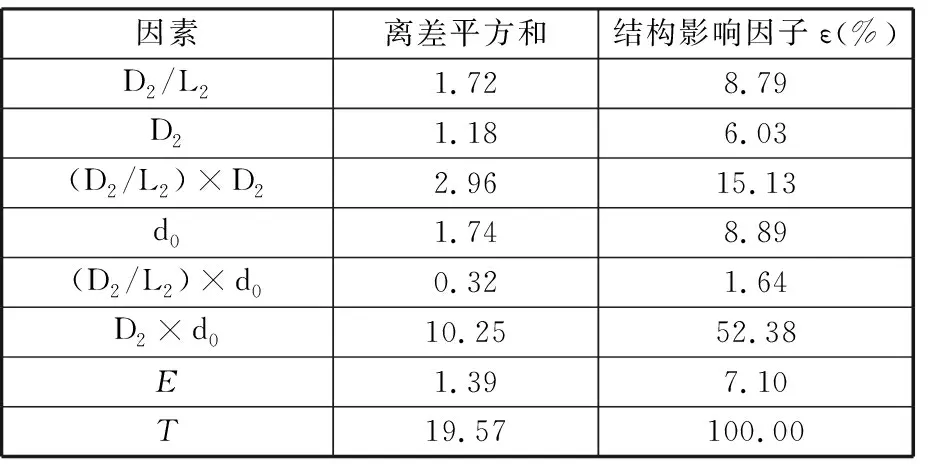
表9 连杆轴颈冗余强度试验方差值

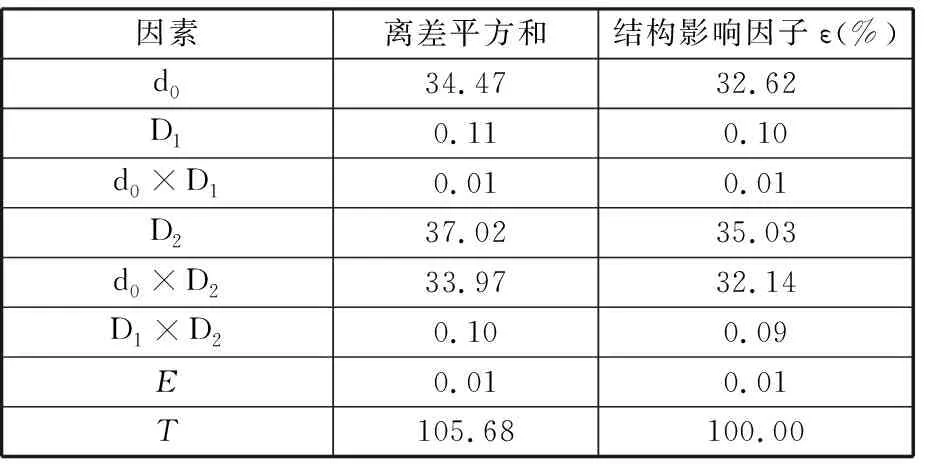
表10 油孔冗余强度试验方差值

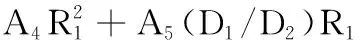
其中，A0～A5、B0～B8、C0～C5分别为各项系数，将其数值代入拟合函数，分别为

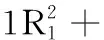
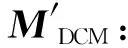
φ11=0

φ21=(B3+B8D2)d0+B6D2φ22=0

φ25=0φ31=(C1+C5D2)d0+C3D2

首先对冗余强度小于0的结构进行优化，再对冗余强度小于1.25的结构进行优化，当优化后的零件整体冗余强度r≥1.25时(即满足产品下一生命周期的使用)完成优化。分别取d0、D1、D2、R1、L2的优化步长为0.2、1、1、0.2、1。

零件的原始设计参数如下：d0=7 mm，D1=92 mm，D2=76 mm，L2=46 mm，R1=6 mm，r1=1.126 3，r2=-0.047 3，r3=-0.086 9。由于r2,r3<0，故以r2、r3为优化对象，其单调性矩阵如下：

其中，“+”表示结构冗余强度关于设计参数单调递增;“-” 表示结构冗余强度关于设计参数单调递减;“0”表示无关系。在进行结构冗余强度优化时，需要选择单调性一致的设计参数进行优化，否则就会出现优化某一结构而导致另一结构劣化的现象，故选取优化参数d0、D2、L2。

零件第1次优化的设计参数如下：d0=6.8 mm，D1=92.0 mm，D2=77.0 mm，L2=47.0 mm，R1=6.0 mm，r1=0.969 0，r2=0.252 1，r3=0.269 1。由于r1,r2,r3<1.25,故以r1、r2、r3为优化对象，其单调性矩阵如下：

则选取优化参数d0、D1、L2、R1。

零件第2次优化的设计参数如下：d0=6.6 mm，D1=93.0 mm，D2=77.0 mm，L2=48.0 mm，R1=6.2 mm，r1=1.129 0，r2=0.387 0，r3=0.849 3。由于r1，r2,r3<1.25，故以r1、r2、r3为优化对象，其单调性矩阵如下：

则选取优化参数d0、D1、L2、R1。

本文省略零件第3次至第11次的优化过程，则零件第12次优化的设计参数如下：d0=6.6 mm，D1=99.0 mm，D2=80.0 mm，L2=47.0 mm，R1=6.2 mm，r1=1.482 7，r2=1.079 4，r3=2.203 7。由于r2<1.25，故以r2为优化对象，其单调性矩阵如下：

则选取优化参数d0、D2、L2。其优化结果如下：d0=6.6 mm，D1=99.0 mm，D2=81.0 mm，L2=48.0 mm，R1=6.2 mm，r1=1.300 6，r2=1.347 8，r3=2.699 2。零件整体的冗余强度r为1.300 6，满足冗余强度条件，优化过程结束。

由上述结论可知，在原尺寸基础上，D1增大7 mm，D2增大5 mm，R1增大0.2 mm，d0减小0.4 mm，L2增长2 mm。优化结果符合柴油机设计手册的优化经验，优化后零件整体冗余强度r为1.300 6，与初始状态相比，有较大提升且满足冗余强度条件。

4 结论

(1)针对主动再制造零件结构设计过程中存在的问题，以系统思维方式研究零件各结构间的耦合关系，提出了结构功能耦合系统的概念，直观地展现了结构间的耦合作用规律，并给出了结构功能耦合系统模型的建立方法。

(2)在结构功能耦合系统模型建立的基础上，提出了主动再制造在零件层级的设计方法，解决了再制造设计过程中优化某一结构而导致另一结构劣化的问题，以曲轴为例进行了方法验证。

(3)所提设计方法有较强的普适性，但也存在一定程度的局限性，如本文的数据收集主要是通过仿真试验来获得，而没有条件从多方面进行验证。