弹体飞行姿态角速度磁测解算方法*

陈春行,林春生,马剑飞,翟国君

(1 海军工程大学兵器工程系,武汉 430033;2 海军工程大学导航工程系,武汉 430033;3 海军海洋测绘研究所,天津 300061)

0 引言

随着现代战争信息化及常规弹药制导化的发展,如何获得旋转弹体的姿态角速度已经成为一个重要的研究方向[1]。通常情况下弹体的姿态角速度是通过陀螺完成,而由于旋转弹体常处于高动态、高冲击、安装空间有限的应用环境,常规陀螺抗过载能力不强且体积过大,而MEMS陀螺受其量程与精度的限制,导致其可靠性变差,因此两者均不适用于弹体姿态角速度的测量[2-3]。文献[4]提出了一种基于地磁组件的角速度测量方法,该方法采用磁传感器获得大地磁场强度在弹体坐标轴上的投影及其变化率,并利用卡尔曼滤波器获得滚转角速度。但由于其通过单轴陀螺仪测得滚转角速度,因此该方法只能用于非高速旋转弹体。文献[5]基于所建立的旋转弹的简化动力学模型,提出采用双轴正交加速度计测量横轴与竖轴上的加速度值,实现对弹体俯仰角速度和航向角速度的测量,但该算法仅适用于弹体纵轴轴向速度已知的情况。文中针对以上算法的不足,提出了一种利用三轴地磁传感器测定弹体姿态角速率的方法,有效的解决了自旋弹姿态角速度测量的问题,且满足精度要求。

1 地磁传感器测量角速度原理

如图1所示,建立发射坐标系oxyz(原点在大地发射点),ox轴指向目标为正,oz轴垂直地面指向下,oy轴与ox,oz轴构成右手坐标系。地磁场方向和大小用B表示,其在oxy面内的投影与ox轴的夹角定义为磁方位角H,由ox轴偏向oy轴正方向取正。磁倾角I为地磁场与oxy的夹角,向下为正。图2为三轴地磁传感器在弹体的三个敏感轴上的配置方式,用于感知地磁场在弹体坐标系o1x1y1z1(原点为弹体质心)上投影的分量大小及变化率。ωx1,ωy1,ωz1分别为弹体坐标系相对于地面坐标系的转动角速度沿弹体坐标系各个轴上的分量。

弹体在短距离飞行过程中地磁场矢量基本保持不变,可将其视为常量。则由图1可得地磁场在发射坐标系oxyz上各轴的投影分量为:

(1)

根据发射坐标系与弹体坐标系之间的的转换关系可以进一步得到弹体坐标系上各轴地磁场的投影分量:

(2)

式中：

式中:θ、γ、φ分别为弹体相对于发射坐标系的俯仰角、滚转角、和偏航角,Bx1,By1,Bz1可由三轴地磁传感器测得。

图3为弹体截面图,ωyz为弹体的转动角速度在弹体横截面上的投影,ωy1,ωz1为ωyz在弹体坐标系中o1y1轴和o1z1轴上的投影分量,ωy2,ωz2为ωyz在弹轴坐标系o1y2轴与o1z2轴上的投影分量。

由图中几何关系可知,ωy1,ωz1和ωy2,ωz2之间的转换关系为:

(3)

再根据外弹道知识可知[6],自旋弹的质心方程为:

(4)

将式(3)和式(4)进行整合可得到弹体姿态角的变化率与弹体相对转动角速率之间的关系为:

(5)

2 滚转角速率量测方程

为了便于研究,假设弹道处于标准气象条件下,弹体的质量均匀分布,且不考虑弹体转速的衰减,则在弹体飞行过程中,地磁传感器所输出的x,y轴的信号近似为周期信号,两轴信号呈现一定的相关性。图4为y、z两轴的磁场仿真信号,两轴信号为正、余弦曲线,y轴信号在前,z轴信号在后,两者之间的时间延时约为1/4个周期,相位差为π/2,则可对短时间T内磁场信号By、Bz分量做相关运算如下:

(6)

该时间段内,弹体可近似看成做匀速转动,那么任意时刻t时y轴和z轴所转动的角度为γr=ωrt,则可通过(6)式求得Ryz(τ)max所对应的时间延时τ0进而求解出时间T内的滚转平均角速度ωr:

ωr=π/(2τ0)

(7)

3 俯仰角速度和偏航角速度量测方程

根据文献[7]可知,地磁场在发射坐标系中对于时间的导数等于地磁场在弹体坐标系上对于时间的导数加上地磁场本身和弹体转动的角速度矢量乘积,即:

(8)

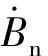
(9)

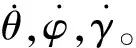
4 仿真试验

给定初始条件:地磁场50 000 nT,磁倾角I=60°,方向斜向下,初始磁航向角H0=15°,弹体滚转角速率为6(1+0.05sin(π/12)) r/s,俯仰姿态从-40°到40°(下压为正),偏航角为π/12,算法采样率为720 Hz,采样时间为55 s,为模拟真实的弹道参数,将仿真出来的磁场测量值添加上均值为0,方差为0.1 uT的高斯白噪声。仿真所求得的姿态角速度误差如图5-图7所示。

从仿真实验结果可知:运用地磁传感器解算姿态角速度不随误差积累,俯仰角速度误差与偏航角误差均保持在±0.8°/s以内。滚转角误差则控制在±1°/s,以上表明姿态角速度测量误差处于合理范围之内,且算法简单易于实现,能够应用于弹体姿态角速度测量。

5 结论

文中分别建立了弹体欧拉角速度的量测方程,根据旋转弹体横截面上地磁传感器两轴所测的磁场信号呈现相关性的特征,利用相关函数的最大值点估计解算出弹体的滚转速度,进而求得其俯仰角速度和偏航角速度。仿真结果表明该算法对于弹体姿态角速度测量满足精度要求,在工程上是可行的,但无法克服地磁盲区与周围磁场的干扰,具有一定的局限性。