腹板受拉L形钢筋混凝土柱的有限元分析
2018-11-12李文南锐锐
李文,南锐锐
(东北石油大学,黑龙江 大庆 163318)
钢筋混凝土异形柱避免了矩形柱向外突出的楞角,可使房间内部更美观,并增加了建筑的实际使用面积,更利于室内空间的充分利用,同时提高了房屋的商业价值,因此在住宅建筑中的应用逐渐增多。随着《混凝土异形柱结构技术规程》(JGJ149-2006)[1]的颁布,使得异形柱的建造更加规范、安全和广泛,同时建筑上的大量应用也相应地推动了学者进一步的深入研究。当前,在多数建筑中L形钢筋混凝土柱腹板处于受压状态,也存在着少量腹板受拉的情况,如框架结构角柱的外侧受到出挑的重物作用时,由典型的双向偏压变为腹板受拉。目前国内对腹板受压的L形柱研究较多,而对于腹板受拉的L形柱研究较少。王丹、黄承逵等[2]对10根L形柱进行了双向偏压试验,得出了大小偏心受压破坏形态,给出了可用于配筋设计和承载力验算的正截面承载力相关曲线,且明确了荷载加载角对L形柱的中和轴位置影响极大;杨溥、唐剑等[3]从承载力、刚度和延性三个方面讨论了不同轴压比的钢筋混凝土柱在不同加载方向的水平力作用下的受力性能;徐士弢[4]从偏心距、加载角、混凝土强度和配箍率4个参数对5根不等肢L形柱进行了双向偏压的力学性能试验。本文将对腹板受拉的等肢L形钢筋混凝土柱进行数值模拟,分析不同影响参数对L形柱抗压弯承载能力的影响。
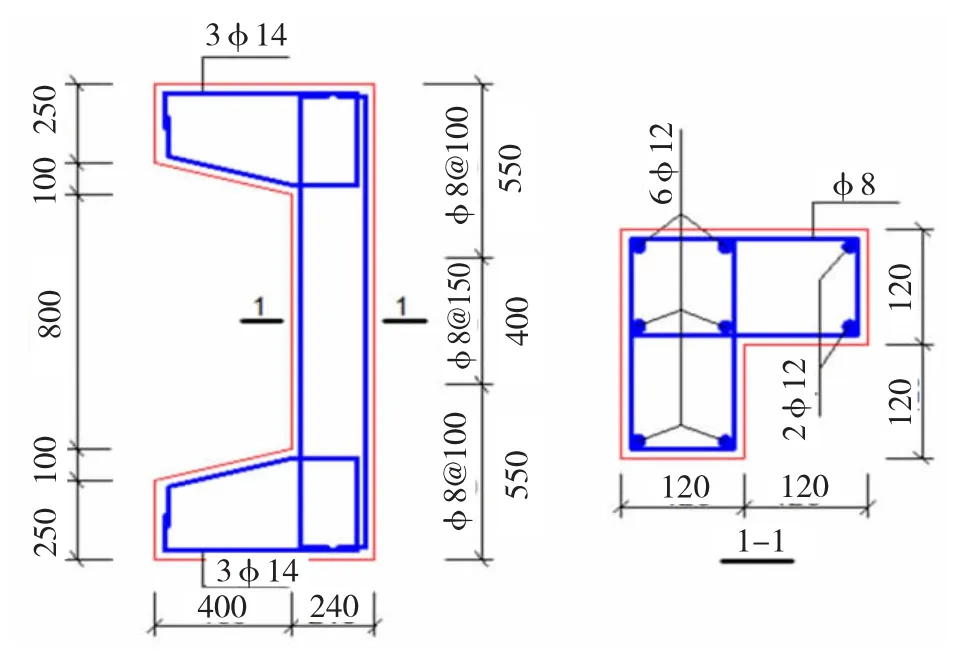
图1 试件尺寸及配筋(mm)Fig.1 Section and reinforcement details of the specimen
1 有限元分析模型
为了进一步深入探讨腹板受拉L形钢筋混凝土柱的受力和变形性能,采用参考文献[5]中的几何参数和材料参数,基于有限元软件ABAQUS对文中的腹板受拉L形钢筋混凝土试件Z1(图1)进行数值模拟,验证本文建立的有限元模型的正确性。其中混凝土强度为C30,轴心抗压强度取23.12 MPa,弹性模量取30 GPa;纵向钢筋直径为12 mm,屈服强度取375 MPa,极限强度取550 MPa,弹性模量取200 GPa。试验加载装置见图2。
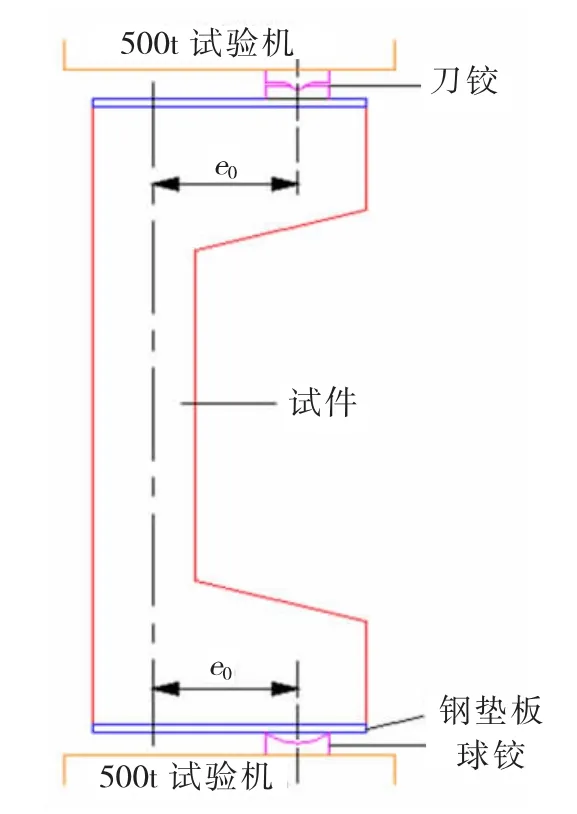
图2 试验加载装置简图Fig.2 Layout of test setup
1.1 材料本构模型
混凝土本构关系采用软件ABAQUS自带的塑性损伤模型(Concrete Damaged Plasticity,简称 CDP模型)[6-7],混凝土应力-应变全曲线(图3和4)方程采用混凝土结构设计规范[8]中建议的公式[6,9-10]。受压应力-应变曲线的弹塑性分界点根据陆新征等人[11]的建议取0.4fc(fc为轴心抗压强度)。混凝土塑性损伤模型参数中,膨胀角取30°,流动势偏移值取0.1,双轴极限抗压强度与单轴抗压强度比取1.16,拉伸子午面上和压缩子午面上的第二应力不变量之比取 0.667,对多个粘性系数 0.0005、0.0003、0.0001等进行反复试算,参考相关文献[12-14]最终取0.0003。经计算,混凝土受压和受拉的本构参数分别见表1。
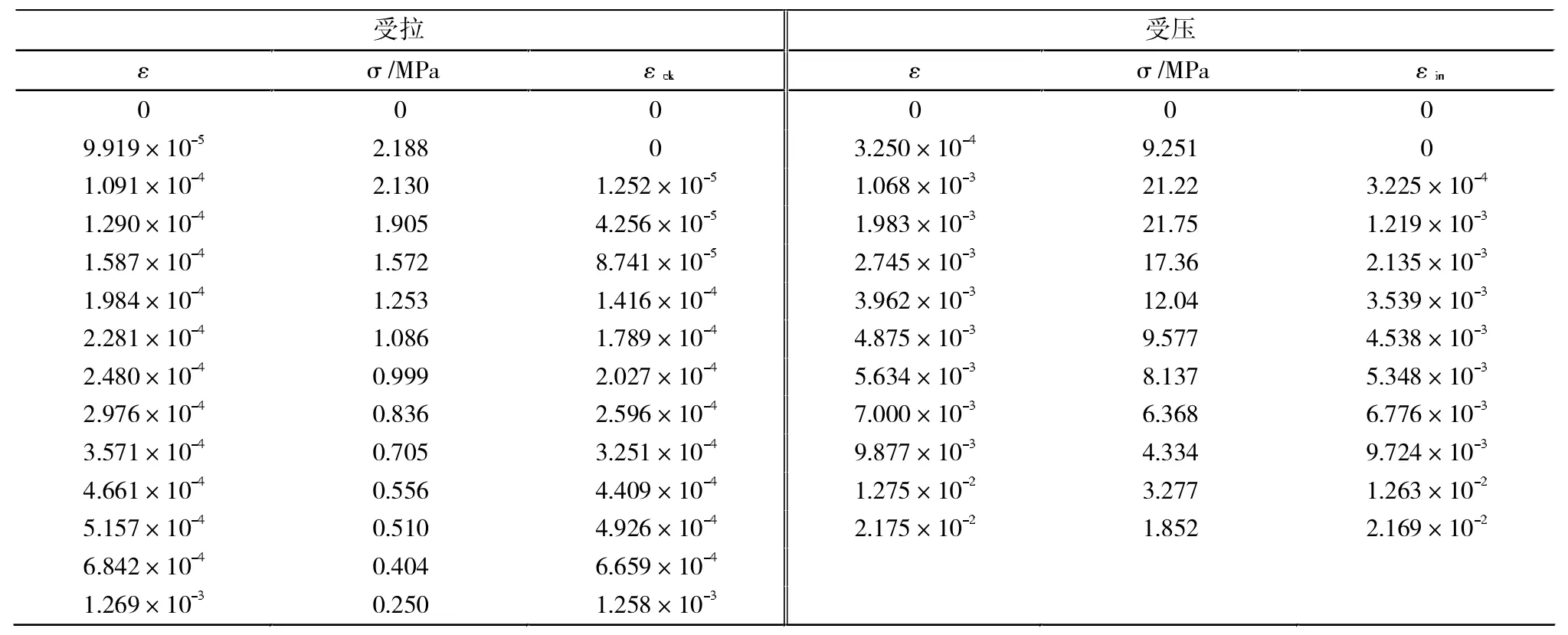
表1 混凝土受拉、受压本构参数Tab.1 Parameters in the constitutive law for concrete in tension and compression
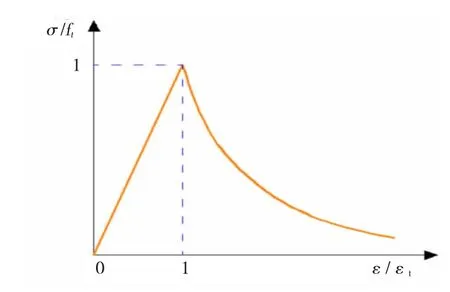
图3 混凝土受拉应力-应变曲线Fig.3 Tensile stress-strain curve of the concrete
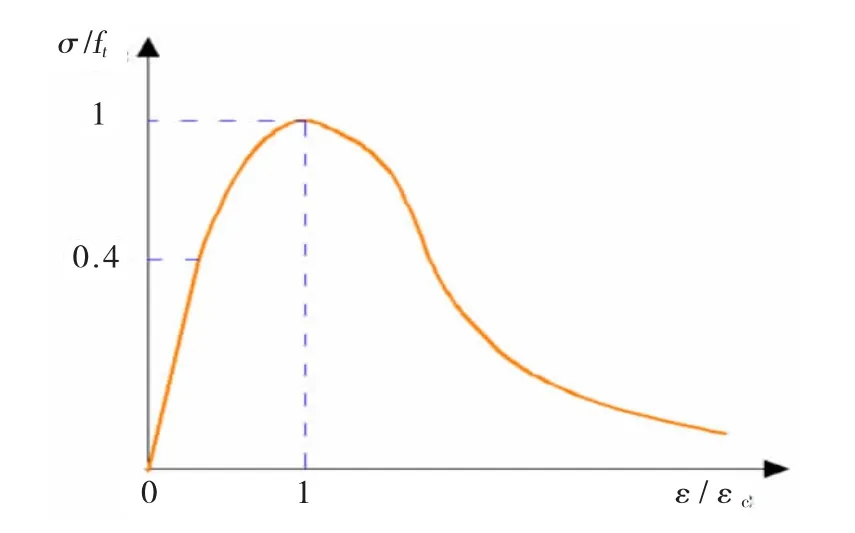
图4 混凝土受压应力-应变曲线Fig.4 Compressive stress-strain of the concrete
钢筋单调加载应力-应变本构关系曲线来自Esmaeily-Xiao模型[15-16],该模型(图 5)能反映单调加载时的屈服、硬化和软化现象。参数k1为钢筋硬化起点应变与屈服应变的比值,取4;k2为钢筋峰值应变与屈服应变的比值,取25;k3为钢筋极限应变与屈服应变的比值,取40;k4为钢筋峰值应力与屈服强度的比值,取1.2。
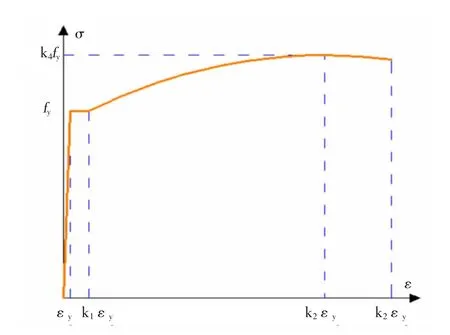
图5 Esmaeily-Xiao模型Fig.5 Esmaeily-Xiao model
1.2 模型建立
混凝土采用C3D8R(8节点六面体线性减缩积分单元),该单元对位移的求解结果较准确,网格存在扭曲变形时,分析精度不会受到大的影响,而且在弯曲荷载下不容易发生剪切自锁。采用T3D2(2结点线性桁架单元)来模拟钢筋,纵筋和箍筋装配在一起的钢筋骨架与混凝土之间的约束定义为“Embedded Region”,实现钢筋单元与混凝土单元的变形协调,并可以将钢筋骨架和混凝土分别显示,方便考察各自的性能[17-18]。异形柱的两端分别设置20 mm厚的钢垫板,以防柱端先于柱身破坏,钢板和柱端之间的约束用“Tie”来定义。
为了准确施加荷载和设置支座约束,在L形柱的上下两端表面用分割工具(Partition)分别划出支座区域,并在加载点处分别定义2个参考点RP-Top和RP-Bottom,将参考点与支座区域建立Coupling约束[1 9]。根据试验实际情况,柱底端支座区域设置为固定约束,柱顶端支座区域设置为可施加Y向位移的约束;在柱顶端参考点RP-Top上施加一个沿Y轴负方向位移进行荷载。L形混凝土柱有限元模型如图6所示。由图6可知:计算值与试验值趋势吻合良好。
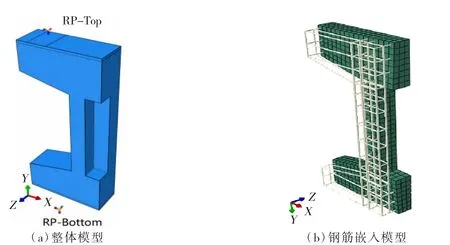
图6 L形钢筋混凝土柱有限元模型Fig.6 Finite element model of the L-Shaped reinforced concrete column
2 有限元模型验证
利用上述模型,采用位移加载的方式,对L形柱试验的荷载-柱中挠度曲线进行验证,结果如图7所示,其承载力及相应的挠度值见表2。
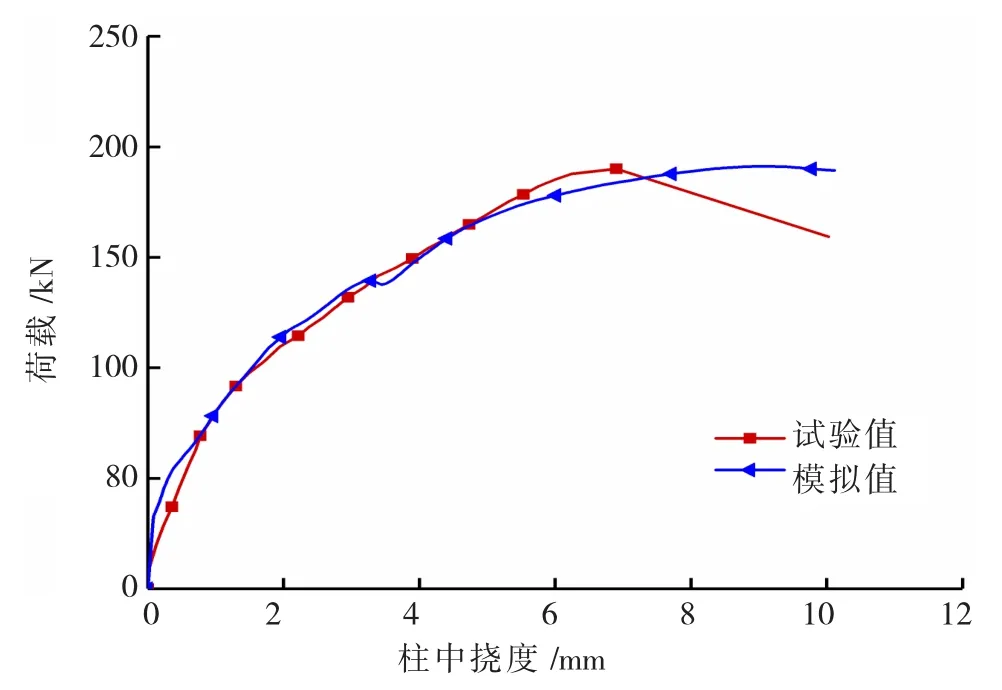
图7 荷载-柱中挠度曲线Fig.7 Load-versus-midspan deflection curves

表2 极限承载力及柱中挠度Tab.2 Ultimate bearing capacity and midspan deflection
从表2可知:极限承载力相差不大,而最大荷载对应的挠度值偏差较大。经分析,导致挠度偏差较大的主要原因有二:一是试验中实际测量点的位置与有限元模拟对应点的位置有稍许偏差;二是有限元模型中未考虑箍筋对混凝土的约束情况,腹板受拉侧柱中混凝土比实际所受的约束减弱。
3 参数分析
选取试件Z1为基本构件,分别依次改变荷载偏心距e、加载角α、混凝土强度、纵筋配筋率ρ来进行参数分析,有限元试件材料相关参数见表3和表4。
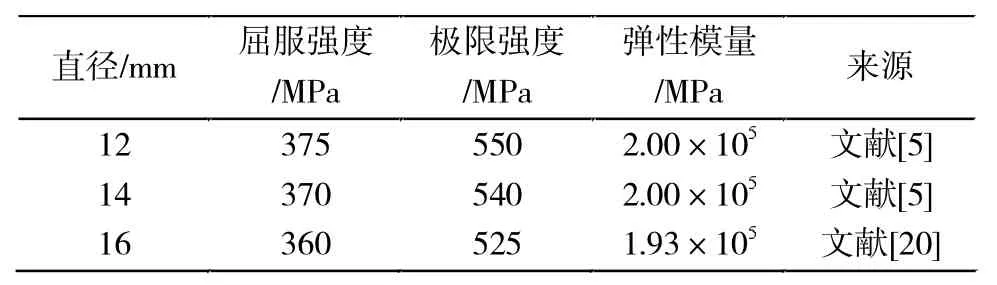
表3 钢筋基本力学性能Tab.3 Mechanical properties of reinforcement
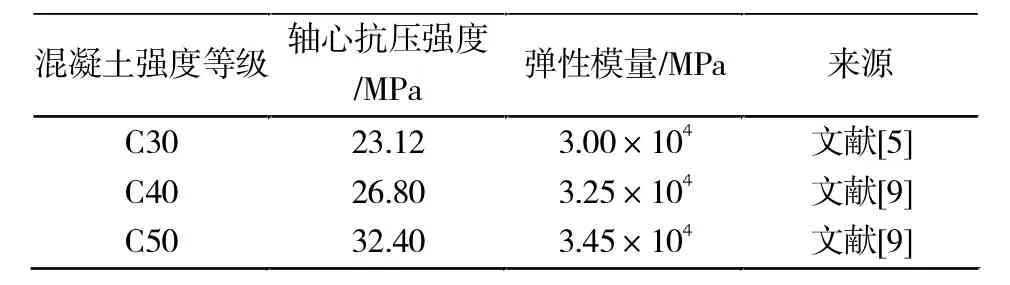
表4 混凝土基本力学性能Tab.4 Mechanical properties of concrete
3.1 荷载偏心距
图8a至e分别是不同偏心距e下L形柱的荷载和柱中挠度关系曲线[21],结果表明:
从曲线总的趋势来看,构件的承载力随着偏心距的逐渐增大而逐渐减小,延性也随着偏心距的逐渐增加而逐渐提高。
其中,偏心距从299-339 mm构件在偏心角0°、45°、80°、100°、135°下,异形柱极限承载力分别降低了 16.81%、45.54%、1.38%、1.65%、12.76%,339-379 mm构件分别降低了 17.71%、23.72%、3.55%、1.07%、19.22%。从以上数据可知:偏心距的变化对承载力变化率的影响近似正比关系,而另一个即将讨论的参数加载角的变化对承载力变化率的影响是较大的。因此,偏心距对L形柱的承载力影响较大,且应宜与加载角一起考虑。
3.2 荷载加载角
图8f至h分别是不同加载角α(图9)下L形柱的荷载和柱中挠度关系曲线[22-23],结果显示:构件的加载角依次从 0°逐渐增加到 45°、80°、100°、135°,极限承载力在偏心距为299 mm下的变化率分别为134.97%、127.90%、-2.74%、-60.64%,在偏心距为339 mm下的变化率分别为 53.27%、314.24%、-3.01%、-65.09%,在偏心距为379 mm下的变化率分别为42.59%、421.88%、-0.51%、-71.50%。从曲线趋势和以上的极限承载力变化率可以看出:L形柱的极限承载力在加载角从0°至180°呈现先上升后下降的趋势,延性的变化规律和承载力一致。这是因为荷载加载角直接影响着L形柱截面的受压区高度,随着加载角的的变化,受压区高度也经历了先变大后变小的过程,受压区高度增大,承载力提高,受压区减小,承载力降低。因此,在L形柱设计时,荷载的加载方向应慎重考虑。
3.3 混凝土强度
图8i至k分别是不同混凝土强度下L形柱的荷载和柱中挠度关系曲线,这些曲线显示:构件的混凝土强度从C30逐渐增加到C40、C50,极限承载力在偏心距为299 mm 下提高了5.97%、5.73%,偏心距为339 mm 下提高了5.28%、5.51%,偏心距为379 mm 下提高了7.84%、7.09%。这表明:随着混凝土强度的逐渐提高,L形柱的承载力也逐渐提高,且变化趋势平缓。故在L形柱构件设计时,增大混凝土强度不失为一种提高承载力的措施。
3.4 纵筋配筋率
图8l至n分别给出不同纵筋配筋率ρ下L形柱的荷载和柱中挠度关系曲线,结果显示:构件的纵筋配筋率从1.57%依次提高到2.14%、2.79%,极限承载力在偏心距极限承载力在偏心距为299 mm下提高了19.78%、11.35%,偏心距为339 mm下提高了17.76%、16.88%,偏心距为379 mm下提高了14.83%、20.75%。这表明:随着配筋率的提高,构件的承载力也随之提高,且对承载力的影响较大。
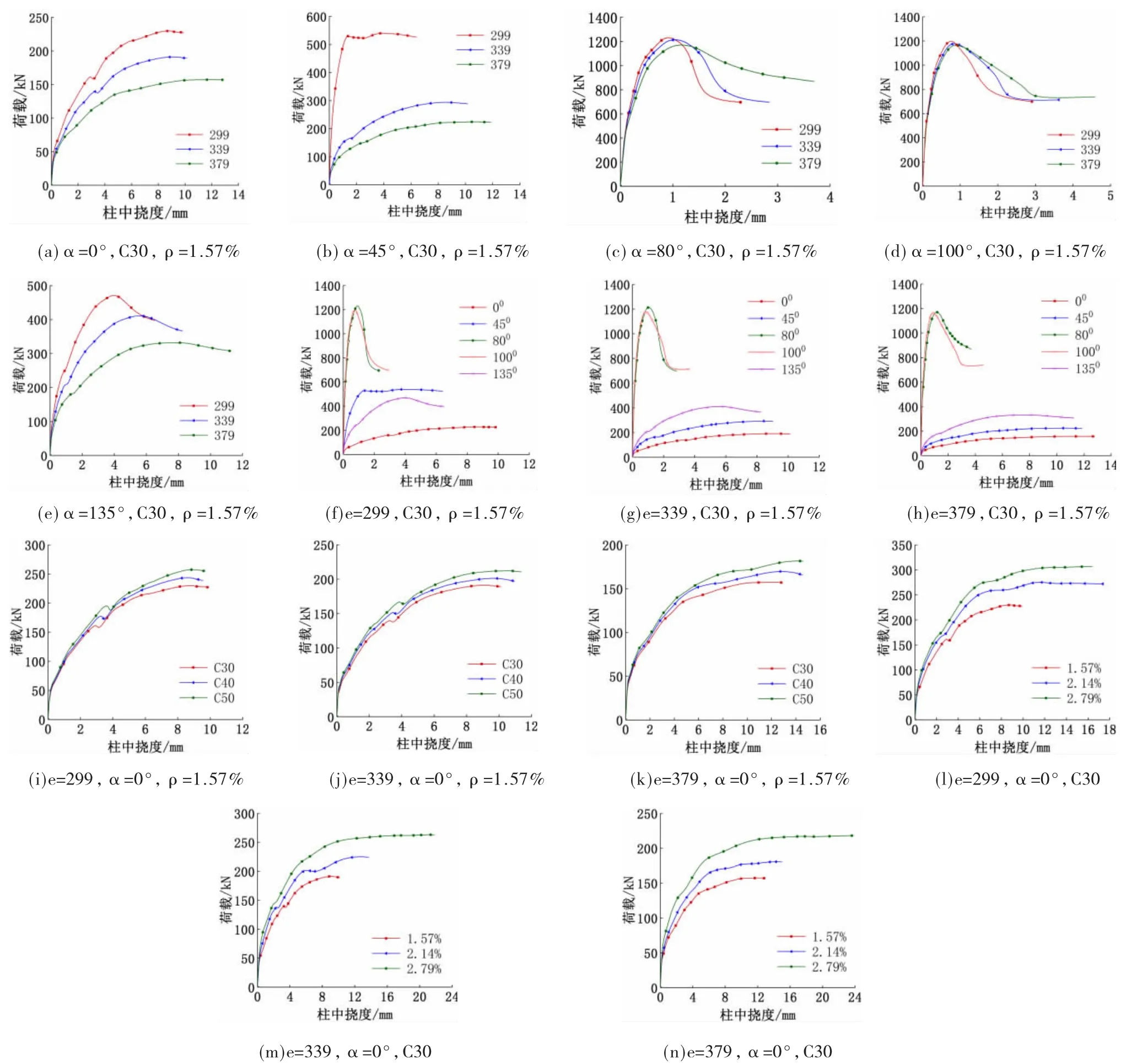
图8 不同参数对柱承载力的影响Fig.8 Influence of different parameters on bearing capacity
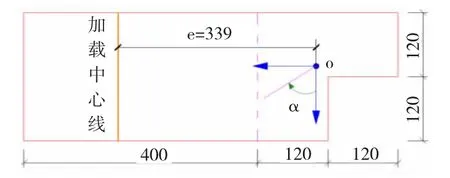
图9 加载角α定义Fig.9 Definition of loading angle α
4 结论
本文利用有限元软件主要对腹板受拉L形钢筋混凝土柱的承载力进行了分析,得出以下结论:
(1)混凝土采用ABAQUS自带的混凝土塑性损伤模型和规范给出的应力应变曲线,钢筋采用Esmaeily-Xiao模型可以很好地模拟偏心作用下腹板受拉L形钢筋混凝土柱的荷载-柱中挠度曲线。
(2)偏心作用下腹板受拉L形钢筋混凝土柱的承载力,随着偏心距的增大而减小,随着加载角从0°增至180°先上升后下降,随着混凝土强度和纵筋配筋率的提高而提高。
(3)对于腹板受拉钢筋混凝土L形柱,荷载的加载角对构件的承载力影响极大,故设计构件时,应充分考虑加载角这一参数。
