带运输时间和单自动机的流水作业排序

时凌，张琼，时义梅，刘丁酉*

（1 广州工商学院基础教学部，广东 广州 510850；2 湖北民族民族学院理学院,湖北 恩施 445000;3 武汉大学数学与统计学院, 湖北 武汉 430072）

带运输时间和单自动机的流水作业排序问题可叙述为:假设给定由m台机器构成的机器集{M1,M2,...,Mm}和由n个工件组成的工件集{J1,J2,...,Jn}。每个工件Jj均有m道工序Qi,j(i=1,2,...,m;j=1,2,...,n),其加工顺序Q1,j→Q2,j→...→Qm,j，其中，每道工序Qi,j在机器上Mi的加工时间为pi,j(pi,j≥0)。每台机器在同一时间只能加工一个工件。

本文假设一个工件在一台机器上完工后在下一台机器加工之前存在一个时间间隔,即工序Qk,j在机器Mk上完工后,下一道工序Qk+1,j在机器Mk+1上加工之前需要一定的运输时间tj,k(tj,k≥0),所有的运输工作均由自动机R来完成，自动机同一时间也只能对一个工件进行运输。这样工件在运输和加工的过程中就可能会出现一定的冲突。

本文研究的目的是要确定可行排序使完工时间的加权和达到最小,即达到最小,其中Cj是工件Jj最后一道工序Qm,j的完工时间。依据Lawer E L等[1]提出的三元法,带运输时间和单自动机的流水作业排序问题可表示为:,如果不带运输时间和单自动机则可表示为。如果只考虑2台机器,自动机只需在机器M1和机器M2之间运输,运输时间可简化为tj,则该问题可表示为。本文主要研究当所有加工时间均等于1,即时流水作业的排序,即研究排序的复杂性和启发式算法。

现在考虑2台加工机器M1、M2和单自动机R,n个工件在机器M1和机器M2上的加工时间分别为p1,j和自动机的运输时间为tj。

假设序列σ和τ分别表示工件在机器M1和机器上的加工顺序,C(σ,τ)表示问题的最小完工时间。

引理1：考虑具有加工时间pi,j和运输时间

排序问题,则有:

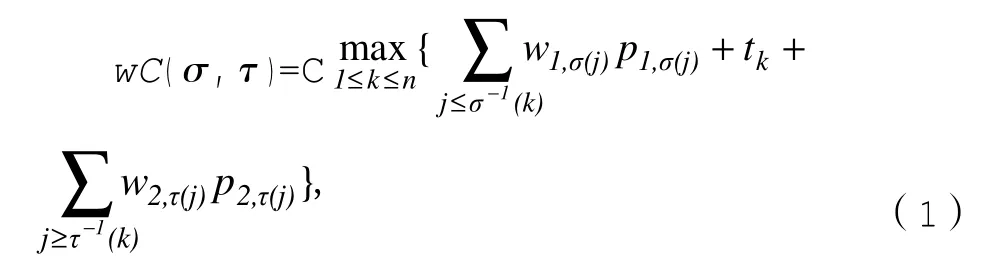
引理1：证明过程与文献[9]相似，本文省略。

定理1：问题是强NP-困难的。

证明：下面利用强NP-困难的3-划分问题[10]到排序问题的归约来证明F2,R1问题是强NP-困难的。

3-划分问题可叙述为:给定正整数集X=和满足条件(2)的正整数b

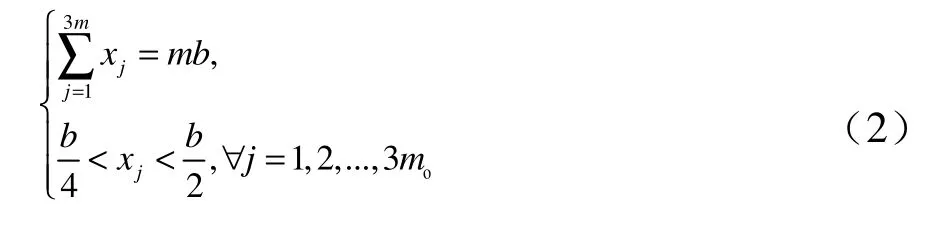
确定集合X是否可以分解为由3个不同元素组成的m个子集{X1,X2,...,Xm}且满足:

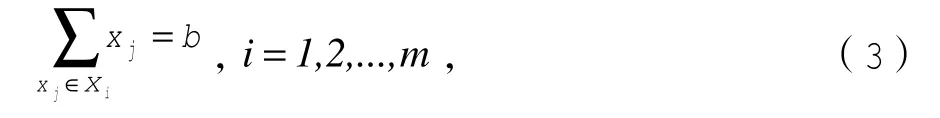
给定3-划分问题的一个实例,构造F2,R1问题的实例:将n=mb+m+1个工件分解为三类:P-工件(划分工件)记为;X-工件(辅助工件)记为;Z-工件(零工件)记为。运输时间和权重由如下公式给出:

(a)划分工件。P-工件满足:

(b)辅助工件。X-工件满足，其中

(c)零工件。Z-工件满足:其中

确定门槛值y=W(X)+W(P,Z),其中。相应的确定性问题为:是否存在加工时间C(S)不超过y=W(X)+W(P,Z)的排序S?

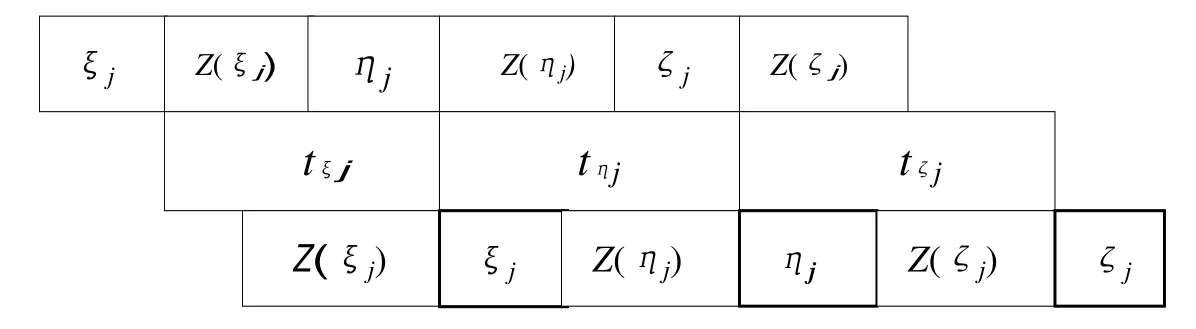
图1 子排序 SjFig.1 Subschedule Sj

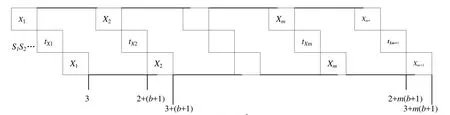
图2 最优排序 S*Fig.2 Optimal schedu le S*

由P-工件得到的最优排序S*和子排序Sj(j= 1,2,…,m)如图2所示。

于是由图1得到一个排序σ,显然这个排序满足wC(σ)≤y。相反假设流水作业排序问题存在满足wC(σ)≤y的排序σ，在式(1)中令k=1,j=n,tj=0,则可得到一个满足wC(σ)=y的排序σ，

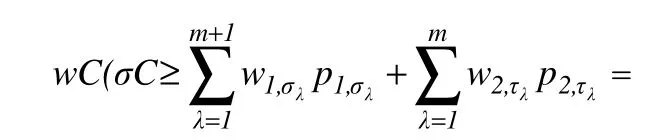
W(X)+W(P,Z)=y，

从而得到了一个满足wC(σ)=y的排序σ。由此可得：

(d)机器M1在区间[0,m(b+1)+1]上加工工件，无空闲;

(e)机器M2在区间[2,3+m(b+1)]上加工工件,无空闲;

(f)自动机R在区间[[1,2+m(b+1)]]上运输工件,无空闲。

不失一般性,假设工件按顺序{1,2,...,m−1,m}加工工件,令X1={i1,i2,...,ik}表示工件X1和工件X2之间的工件集（图3），有X1≠Φ，否则，在工件X1和工件X2中出现空闲，这与上面的(d)-(f)矛盾。

图3 问题在 X1上的子排序Fig.3 Subscheduling for the

下面证明k=3和成立。

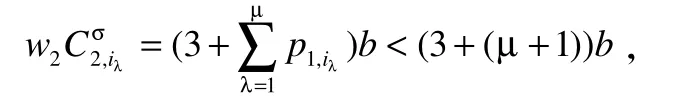
如果k≤2成立,则有:

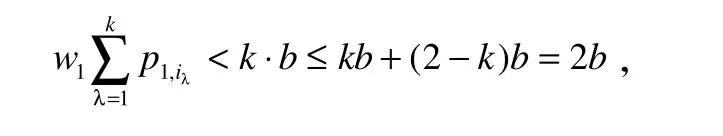
于是自动机R完成工件X1的运输。这样机器M2在工件X1和工件X2之间存在空闲时间，这与上面的(d)-(f)矛盾。

如果k≥4成立,则有:

另一方面,由于工件X1之前需要运输,工件X2不可能在时刻3+b之前在机器M2上进行加工，于是工件X1在机器M2上的完工时间为,工件X2在机器M1上不可能完成集合X1中工件的加工,这与上面的(d)-(f)矛盾。

于是必须有k=3,且自动机R在区间[[2,2+(b+1)]]内运输工件J1和工件J2,所以,即:

另外，由于机器M2在区间[4b,6b]内不存在空闲时间,工件X1在机器M2上必须在时刻3b完工，因此，,又因为=w2,ik=b,所以有:

同理可证明余下的集合X2,X3,...,Xm也是由3个不相同元素组成且满足的3-划分问题的解。

2.1 启发式算法1

步骤1：计算

步骤2：按单调不减的顺序加工工件,即按以下顺序加工工件:

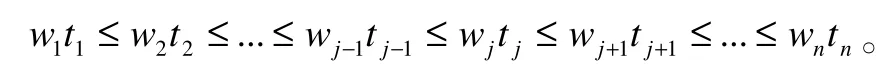
2.2 最坏性能比

设Sj表示工件Jj的开工时间,I1,i表示工件Ji在机器上M1的总空闲时间，表示F2,R1问题的最优排序。

定理2：对于问题,假设SH表示由启发式算法1得到的近似解,则有:且上界是紧的。

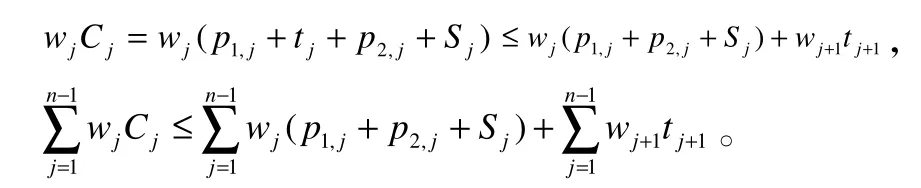
同理可得:

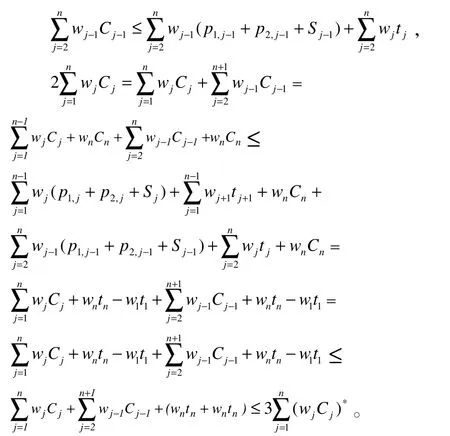
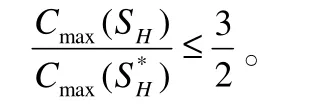
实例1：假设自动机R的运输时间tj(j=1,2,3,4)和权重wj(j=1,2,3,4)如式（6）所示：

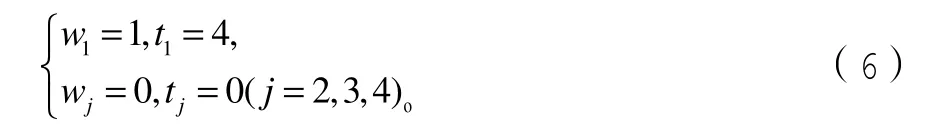
其加工顺序如图4和图5所示。

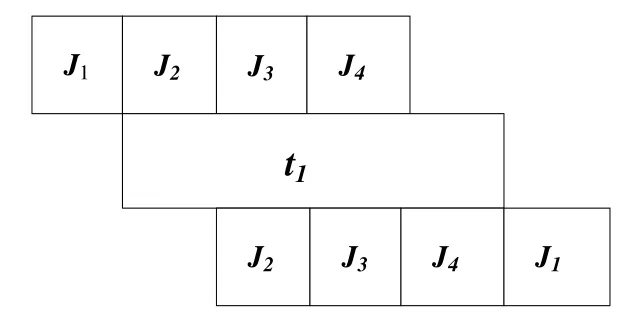
图4 最优完工时间Fig.4 Optimal makespan

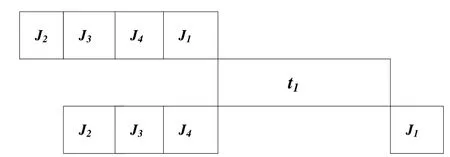
图5 实例1的完工时间Fig.5 Example 1’makespan

定理2得证。

3 小结

(2)更一般的将流水作业排序问题推广到自由作业排序问题,即排序问题时，待解决的问题是如何证明该问题的复杂性，以及如何构造出相应的启发式算法以及对最坏性能比的讨论等等。