基于排列熵的小波包改进去噪算法研究

2018-11-11崔俊周建刘锋

机械工程师 2018年11期

崔俊，周建，刘锋

（1.苏州中材建设有限公司，江苏苏州215000；2.西南科技大学制造过程测试技术教育部重点实验室，四川绵阳621000）

0 引言

工程实践中的信号包含丰富的特征信息但往往也掺杂了干扰噪声，直接对含噪信号进行时频分析可能无法得到准确的分析结论，因此，通常需要对采集到的信号进行降噪预处理。传统的小波包阈值去噪算法阈值的选择无法依据噪声在小波包系数序列中的变化情况进行自适应调整，而小波包分解层数也一般是依据人为经验进行选择，严重影响了去噪效果[1-2]。因此，研究一种新的小波包去噪算法具有十分重要的工程实践意义。

文献[3]针对小波软、硬阈值函数的不足，提出了一种新的含参数的改进阈值函数，能够通过改变参数灵活地调节阈值函数，但并未给出参数的选择标准；文献[4]通过对信号与噪声在小波空间上传播特性的不同进行了分析，提出了一种小波去噪最优分解层数的确定算法，有效地提升了信号的信噪比；文献[5]将信号与噪声难以区分的区域进行分析，使得阈值的估计更加准确，但其方法的实现要求特定性质的阈值函数，不具有适用性。以上方法皆对小波包阈值去噪算法提出了一些改进，虽取得了一定效果，但仍然存在一些不足。

据此，本文综合以上分析，提出了一种基于排列熵的小波包改进去噪算法，并应用于轴承振动信号去噪，结果验证了该方法的可行性与优越性。

1 排列熵算法

排列熵（Permutation Entropy,PE）[6]算法具体计算过程如下：

设一时间序列{X（i）,i=1,2,…,n}，对其进行相空间重构，得到如下矩阵：

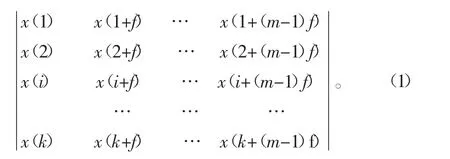
式中：m、f分别为嵌入维数与延迟时间；k=n－（m－1）f。

该矩阵每一行可看作一个分量，共有k个分量。将每个分量中元素按照大小进行升序排列重构，且按照重构前分量元素所在列的索引，可得到k个索引符号序列S（g）其中g=1,2,…,k,k≤m！，m维相空间中共有m！种不同的符号序列，每种符号序列S（g）出现的概率为：P1,P2,…,Pk。则序列排列熵可定义为

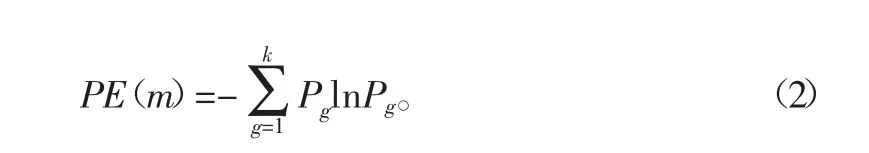
通常需要对PE（m）进行归一化处理，则有：

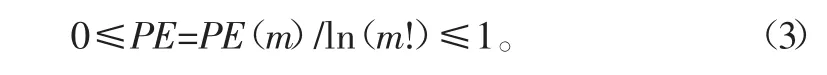
时间序列的随机性程度可以用PE值来表征，值越小，说明时间序列越规则，反之PE值越大，时间序列越随机。实际信号的原始成分往往较有规律，而噪声信号则接近随机，因此可以利用排列熵来说明信号的含噪情况。

为了检验上述排列熵算法在信号中应用是否合理，设定了如图1（a）所示的仿真信号，将该信号分为若干个长度为k的子序列，且每个子序列向后移动一位数据得到下一序列，计算每个序列的PE值且将该值作为中间数据点的PE值，即可得到整个信号的排列熵变化曲线如图1（b）所示（为了同时满足PE值的统计学意义且保证计算的准确性，本文确定m=3,f=5,k=80）。由于上述计算导致的两端缺失PE值按照边缘值进行延拓。

图1 仿真信号及其排列熵

由图1可知，当该信号受到强噪声干扰时（前300采样点）信号排列熵值接近为1，表明此时信号取值处于随机状态，而当噪声消失（300至800采样点），对应的排列熵值迅速减少且在小范围内波动（由于正弦信号的周期性），在800采样点处信号再次受到较弱噪声干扰，此时排列熵值虽有增加，但较左端而言更小。由此可见，可以利用排列熵来表征信号受噪声干扰的情况。

2 小波包改进去噪算法

2.1 小波包阈值去噪原理

含噪信号经小波包变换后，使信号的能量集中在少数几个幅值较大的小波包系数上，而噪声的能量则分布在大部分幅值较小的系数上[7]，因此，对小波包系数进行阈值化处理可以达到去噪目的。

设有被测含噪信号s=x+n，其中x为实际信号，n为噪声，设W与W－1分别为小波变换与逆变换算子，则其去噪具体步骤如下：

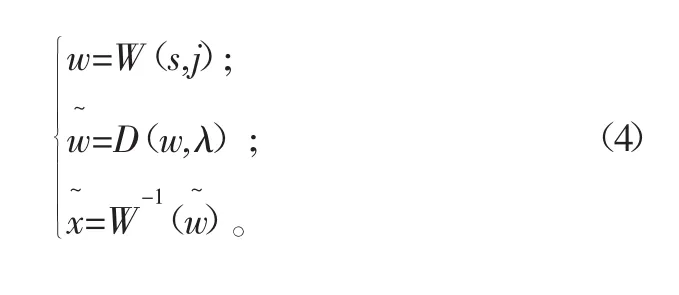
式中：D为非线性滤波算子；λ为阈值，阈值的大小直接影响到去噪结果；j为小波包分解层数，随着分解层数的增加，系数中噪声能量会逐渐减少，但分解层数过多却会导致有用信号成分丢失，因此选择合适的阈值与分解层数对小波包阈值去噪算法非常重要。

2.2 小波包分解层数的确定

小波包分解层数对信号去噪结果有着重要影响，分解层数太小，系数中噪声成分压缩不明显，代表信号的小波包系数与噪声系数幅值相差不大，利用阈值去噪无法达到最佳效果。当分解层数增加到一定数值时，此时小波包系数噪声压缩明显，代表有用信号的系数占主导地位，再继续进行分解得到的系数噪声含量已基本无区别时，此时分解层数可确定为最佳值[8]。因此，确定分解层数的关键在于确定每一层小波包系数的噪声含量，并进行逐层比较，本文利用排列熵对噪声含量进行表征，可将排列熵算法应用于小波包分解层数的确定，具体步骤如下：

1）设定初始分解层数为j=2，最大分解层数为jmax=6；

2）计算第j层与第j－1层的小波包系数对应的排列熵序列且得到其平均值

对不同信噪比（Signal to Noise Ratio,SNR）的仿真正弦信号进行小波包分解且计算不同分解层数的p-值，得到如表1所示数据，且按上述算法将最优分解层数jb列于表中。由表1可知，利用排列熵来确定小波包分解层数可以对含噪较多的信号设定较大的分解层数以尽可能地去除噪声，而对信噪比高的信号分解层数设定较小，以避免信号系数被过度压缩。

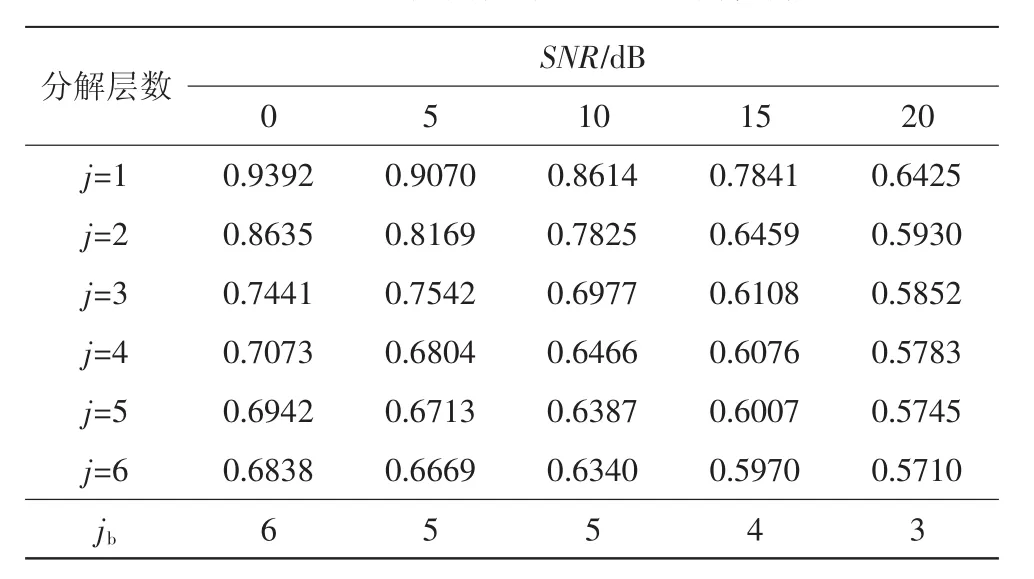
表1 不同分解层数下的排列熵均值

2.3 阈值的估计

由2.2节分析可知，信号经小波分解后不同分解层上的小波包系数噪声含量也不同，传统的全局阈值法对阈值的估计没有考虑小波包系数的噪声分布情况[9]，因此，为了有效地去除噪声，在阈值的估计中，要充分考虑噪声在小波包系数中的变化特征。本文利用排列熵算法来对小波包系数的噪声方差进行估计以选取合适的阈值。根据第一章中介绍的时间序列排列熵计算方法求得最优分解层数小波包系数的排列熵序列，选取最大排列熵所在的小波包系数段，认为此段系数为噪声分布最集中的区域，求得该区域系数模的中值并除以0.6745得到当前分解层数小波包系数的噪声方差估计值σ~，得到阈值为

其中，N为小波包系数长度。

由式（5）可知，该阈值兼顾了噪声的统计学分布特征与小波包系数序列的噪声随分解层数的变化情况，因此能够实现信号与噪声系数的最优分离。

3 实验振动信号去噪分析

为了对本文方法进行验证，以高速深沟球轴承（外圈故障）QC0011286为实验对象，设定转速为60 000 r/min，采样率为10 k Hz，采集到实验振动时域信号如图2所示，由图可知，由于轴承转速较快，振动时域信号振动成分复杂，对其进行去噪后无法直观地从时域信号评判去噪效果。为对不同参数的去噪效果进行定量分析，将各参数去噪后信号的信噪比与均方根误差（Root Mean Square Error,RMSE）列于表2。对原始信号进行功率谱分析得到如图3所示的结果。利用本文方法（m=4,f=5,k=97）选用软阈值函数与连续性较好的sym8母小波对图2所示信号进行分析得到最优分解层数与阈值估计为：j=4,λ=0.31，据此对信号进行去噪得到去噪后信号功率谱如图4所示，且将分解层数与阈值取其他参数进行对比，以分析本文方法的有效性，如图5、图6所示。

表2 不同去噪参数效果对比

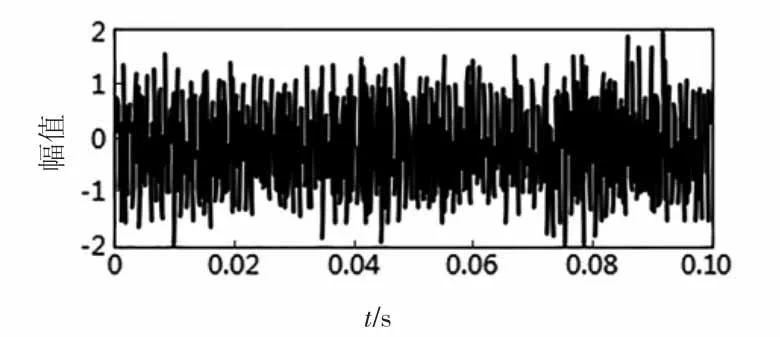
图2 振动信号时域波形

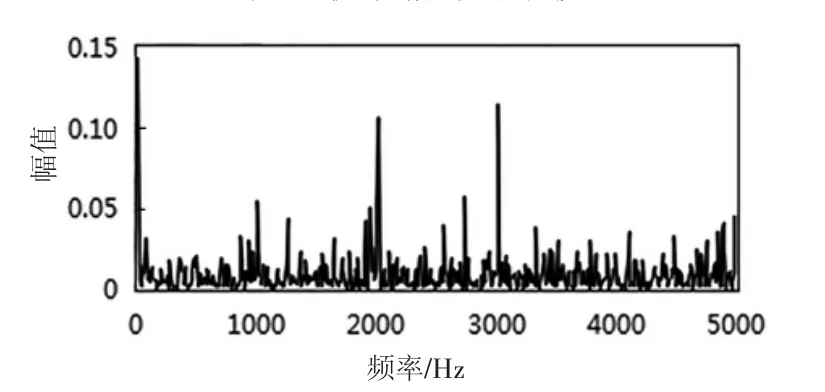
图3 未去噪振动信号功率谱

图4 j=4,λ=0.31时去噪信号功率谱

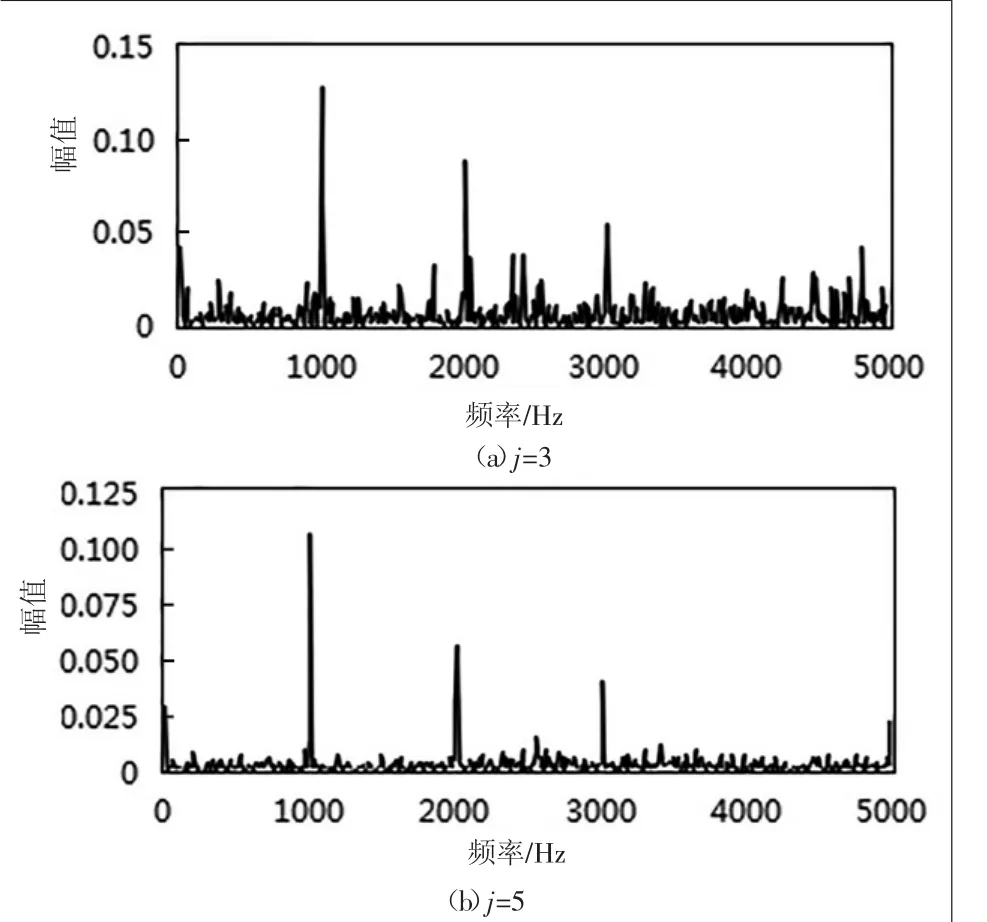
图5 λ=0.31时不同分解层数去噪信号功率谱

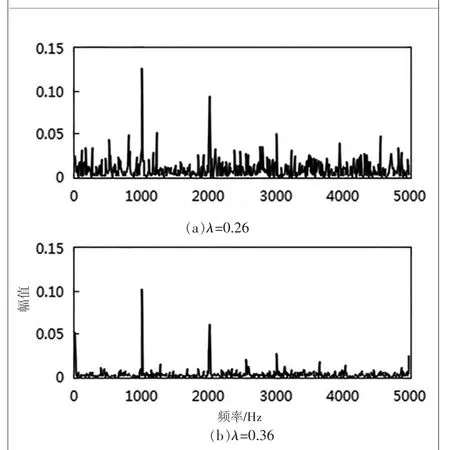
图6 j=3时不同阈值去噪信号功率谱

由图3、图4可知，由于原始振动信号受噪声影响严重，导致其功率谱中干扰频率过多，而经过本文方法去噪后信号，其基频及其倍频1000 Hz，2000 Hz，3000 Hz与轴承外圈故障频率2552.9 Hz清晰可见，去噪效果较好。图5表明当分解层数小于本文确定的最优层数时，噪声去除不明显，而当分解层数过大时，轴承故障频率被过扼杀；由图6同样可知阈值取值大于与小于本文最优阈值皆无法达到较好的去噪效果。表2中数据说明本文提出的基于排列熵的小波包改进阈值去噪算法对振动信号进行去噪后拥有较高的信噪比与较小的均方根误差，利用此方法确定的分解层数与阈值为最优参数，是一种较传统方法更为优越的算法。