小型涵道风机流场的数值模拟与分析

张灵龙， 张建辉， 冯小保， 朱吴迪， 王余彬

（南通润邦重机有限公司，江苏南通226000）

0 引言

涵道风机是指用涵道包围桨叶的气动装置，相对于独立的开放式风机，涵道和桨叶的结合使得桨叶的滑流场发生改变，降低了桨叶尖部的损失，可以尽可能提高整体系统的气动性能[1]，同时由于涵道的保护作用，系统整体的安全性能得到了进一步提高。因此涵道风机被广泛应用于军民航空领域，特别是军用航空无人机领域[2-4]。

目前已有许多学者对涵道风机几何外形对其气动性能的影响有一定的研究，由于涵道和螺旋桨互相干扰的复杂性，高永卫等[5]提出一种将动量定理、轴流式通风机相似理论和旋转机械叶素理论相结合的工程方法，从而缩短了涵道螺旋桨的设计周期。李建波、高正等[6]提出减小桨叶间隙及增加尾扩张角的设计改进方法均可以对涵道风机的气动性能有一定的提升。杜思亮等[7]提出通过桨叶尖部嵌入涵道内壁进一步优化桨叶尖与涵道内壁面的流场特性，以此进一步提升涵道风机的气动特性。

本文基于Navier-Stokes方程和Realizable k-ε双方程湍流模型，采用多参考系将计算域分解为多个子计算域，子计算域间通过interface进行连接，桨叶包含在旋转域中随旋转域一起转动。对建立的涵道风机模型进行不同转速工况下的流场特性计算，通过不同转速下涵道风机流量、动压及轴功率的对比分析，计算结果表明:涵道风机在前期中期加速阶段，其效率呈向上增长趋势；在其后期加速阶段，其效率呈向下减弱趋势;转速3500～4500 r/min是本文计算模型输出效率最可观的工况。

1 数学模型

流体质量守恒方程的积分形式：

式中：ρ为密度；v为速度；V表示控制体；A表示控制面。

式（1）可转化为

式中：ρ为密度；t为时间；u为速度矢量。

动量守恒定律可称为运动方程，或N-S方程，其表达形式为

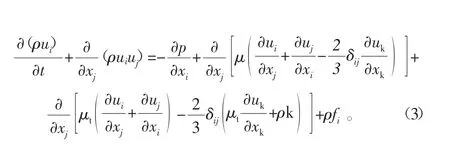
式中：p为压力；k为湍流动能；μ为层流黏度；μt为湍流黏度。

同时，涵道风机内空气流速不超过0.3马赫，因此可认为空气密度是定常量[8]。

Realizable k－ε模型，该模型湍动黏度计算系数Cμ不再是常数，而是对应变率变化的，关于湍动能k和湍流耗散率ε的输运方程：

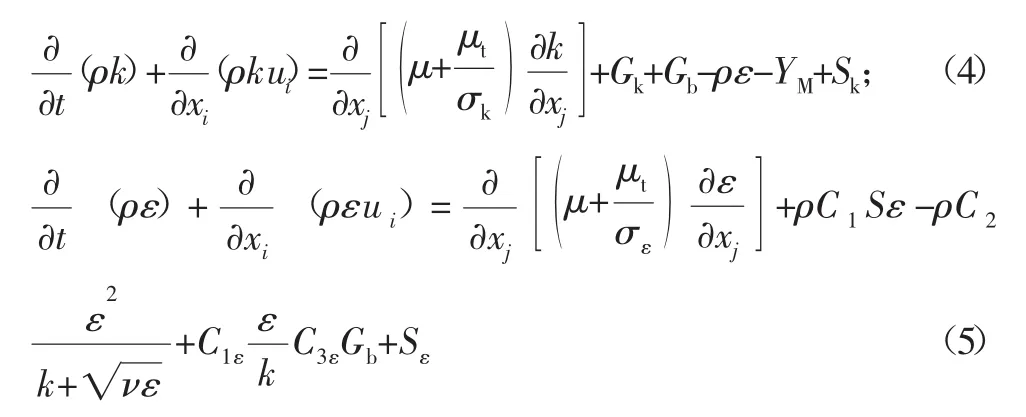
式中：Sij为平均应变张量；在CFD软件中C1ε、C2、σk和σε都是作为默认常数[9]，其中C1ε=1.44，C2=1.9，σk与σε分别是湍动能及其耗散率的湍流普朗特数；ν（m2/s）为分子运动黏性系数；Gb（kg/（m·s3））表示由于浮力影响引起的湍动能产生项；Gk（kg/（m·s3））表示由于平均速度梯度引起的湍动能产生项；YM（kg/（m·s3））表示可压缩湍流脉动膨胀对总的耗散率的影响。

2 物理模型及网格划分

通过三维建模软件建立涵道风机的流场模型，整个模型主要由涵道、桨叶和整流罩等部分组成，桨叶剖面为CLARK-Y翼型，从桨根到桨叶存在20°的线性扭转，桨叶安装角度为15°[10-13]，桨盘直径为360 mm，气体从涵道进风口轴向流入叶片，受到旋转叶片的推挤而排出，最后由涵道出风口流出，整个物理模型如图1所示。

由于桨叶尺寸较小且曲面复杂，因此采用非结构化网格划分。考虑到计算结果的准确性与计算的效率，对桨叶旋转区域网格划分时设置网格的interval size为2，对进出口管道区域网格划分时设置网格的interval size为5，整个计算模型的网格数约500万。其中桨叶旋转区域的网格如图2所示。

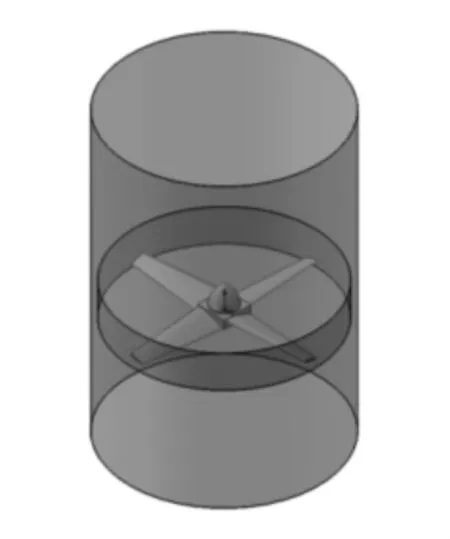
图1 物理模型

图2 叶片旋转区域网格

3 边界条件与求解设置

在CFD求解器中求解设置时，将桨叶旋转区域定义为旋转参考系，采用多重参考系模型（MRF），同时定义旋转域的转速；进口边界条件采用压力进口，并定义入口处气体的湍流强度和水力直径，出口边界条件采用压力出口，初始压力设定为一个标准大气压；旋转区域与静止区域的交界面边界条件定义为interface；此外设置计算模型的壁面边界条件均为固壁为无滑移wall。整个计算模型边界条件的设置如表1所示。

通过对Navier-Stokes方程和Realizable k-ε双方程湍流模型进行稳态求解，采用速度压力耦合方式的SIMPLE算法，对控制方程中的动量方程、质量方程、湍动能和耗散率用二阶迎风格式离散，忽略重力及避免粗糙度对计算精度的影响，同时设置欠松弛因子为0.1，收敛精度均设置为0.0001。

表1 计算模型的边界条件设置

4 计算结果与分析

本文分别计算正反转速1500、2500、3500、4500和5500 r/min，共10组工况，通过模型的子午面 （X=0）来显示流场的压力分布和速度分布。限于篇幅，本文暂且列出正反3500 r/min工况下流场的压力与速度云图。其正转的压力云图与速度云图如图3所示，反转的压力云图与速度云图如图4所示。

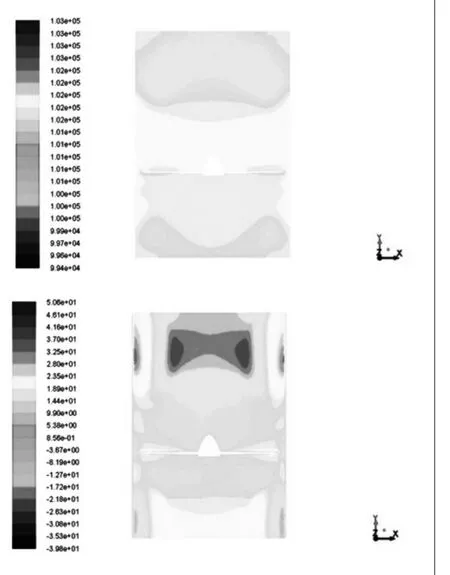
图3 正转3500 r/min工况下子午面的压力云图与速度云图

图4 反转3500 r/min工况下子午面的压力云图与速度云图

通过图3和图4的压力云图可以发现，正转工况下叶片压力面与吸力面的压差要明显大于反转工况下叶片压力面与吸力面的压差，这就说明正转工况下涵气流速。因此可以得出，相同转速下，正转工况时风机的性能要优于反转工况。同时通过CFD后处理输出涵道风机的推力和转矩，获得了正转叶片输出推力和转矩要大于反转叶片输出推力和转矩这一结果。道风机输出的推力值要大于反转工况。通过图3和图4的速度云图可以发现，在桨叶前端正中心形成的低流速区域在反转工况时更加接近于桨叶本身，同时反转工况下桨叶后方的空气流速明显小于正转工况下桨叶后方的空

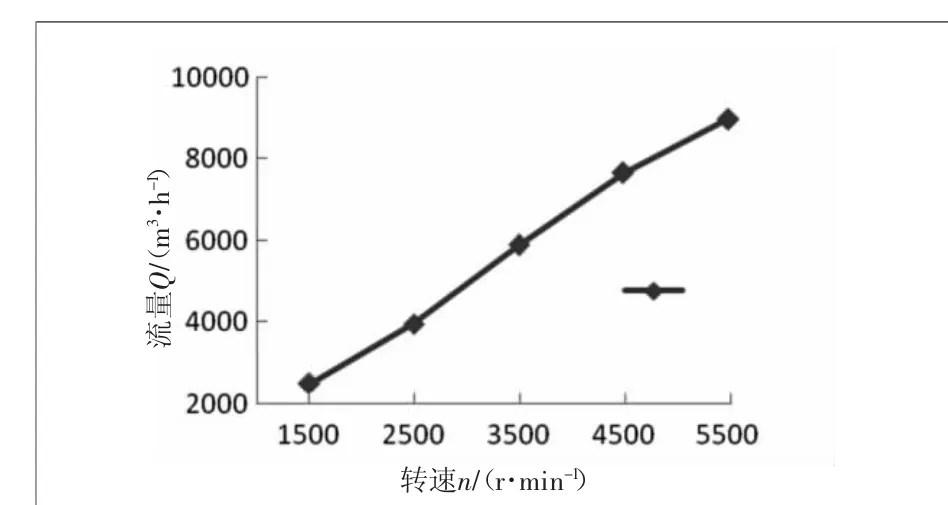
图5 正转工况下流量Q与转速n的关系

图6 正转工况下动压Pd与转速n的关系

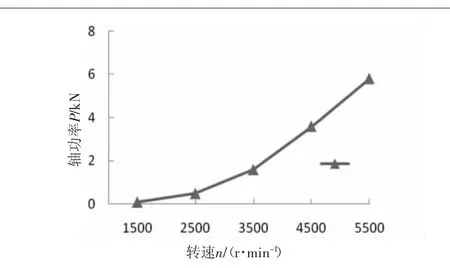
图7 正转工况下轴功率P与转速n的关系

在10组工况仿真计算的过程中，对计算模型的流量Q和动压Pd进行监测，同时输出转矩M来计算获得轴功率P。通过正转5组数据的整理及对比分析，列出其转速与流量Q、动压Pd和轴功率P的关系如图5、图6和图7所示。

通过图5、图6和图7可以发现，随着转速的提升，涵道风机的流量Q、动压Pd和轴功率P，与涵道风机的转速n成正比关系，同时相同增量的转速n，带来的流量Q、动压Pd和轴功率P的增量并不相同，其n-Q、n-Pd和n-P曲线的梯度随着转速n的增加而增大，随之梯度又减小。以上分析表明：涵道风机在前期中期加速阶段。其效率呈向上增长趋势，特别是整个加速阶段的中期阶段，其效率向上增长的趋势更加明显；在其后期加速阶段，其效率呈向下减弱趋势，并且由图5、图6及图7可以看出，转速3500～4500 r/min是本文计算模型输出效率最可观的工况。

5 结 论

本文针对不同转速工况下的小型涵道风机，基于计算流体力学理论和Realizable k-ε双方程湍流模型，建立涵道风机内部流场的数值仿真模型，对其不同转速工况下的流场特性进行了计算与分析。计算结果表明：涵道风机在前期中期加速阶段，其效率呈向上增长趋势，在其后期加速阶段，其效率呈向下减弱趋势，转速3500～4500 r/min是本文计算模型输出效率最可观的工况。