基于悬链线理论的深水REEL型铺设管道张力计算研究
2018-11-11李建楠孙庆辉王双刘军鞠明王晓晓
李建楠, 孙庆辉, 王双, 刘军, 鞠明, 王晓晓
(1.海洋石油工程股份有限公司,天津300451;2.哈尔滨工程大学机电工程学院,哈尔滨150001)
0 引言
随着人类对海洋资源开发的脚步逐渐走向深海,越来越多的海洋开发装备应运而出。为了实现对海洋丰富的资源进行有效开发,各类钻井、采油平台、水下控制系统以及相关作业工具被放置在海上。海底管道作为连接水下生产设施与海上生产平台及陆上岸基设备的主要方式,对海洋能源的开发起着至关重要的作用,当前遍布在世界各地的海洋油气工程普遍采用海底管道作为主要的输送方式,管道运输对原油、天然气的生产、精炼、储存及到用户的全过程都有着十分重要的作用[1]。
海底管道的铺设施工技术作为保证管道安全性的一个重要环节,也随之成为了必须解决的重要问题。在海底管道的铺设过程中,管道的水下部分将会同时受到变形产生的弯矩、张紧器提供的轴向拉力、深水环境造成的静水压力以及环境载荷的共同作用,在如此复杂的海洋环境下为保证管道的安全性,开展深水海底管道铺设水下形态的研究就显得尤为重要[2]。
随着人们对海洋的逐步探索以及海底资源的持续开发,开采技术不断革新,现如今对海洋能源的开发己步入了深水和超深水领域。随着开采水深的不断增加,在进行管道铺设作业时,管道会受到更大的荷载,随之出现了S型铺管法与J型铺管法等管道铺设方式的传统方法。随着人们对管道铺设方式的成本、风险以及效率提出更高的要求,REEL型管道铺设方式作为新兴管道铺设技术随之出现[3]。在不同铺设水深条件下,铺设塔架的角度也不相同,对于REEL型铺设方式,随着水深度的增加,铺设塔角度亦相应的增大,这主要取决于管道在水中所受张紧力、水压以及海洋环境等因素。在这一过程中,管道的受力不能超过其屈服应力,并且要防止管道因受弯矩过大而产生局部的屈曲现象,因此有必要对水中管道受力与张紧力、铺设角和水深之间的关系进行研究。
悬链线理论、有限元分析和差分法等都是求解管道铺设计算问题常用的分析方法,悬链线法是管道受力分析的较为成熟的理论,经常被用于计算管道张力。应用悬链线理论对管道张力进行计算时,将会忽略管道刚度对其的影响,其计算结果对于距离较短的管道会有很明显的影响,但是对于距离较长的管道的影响并不明显[4-5]。因此,应用悬链线法计算管道张力常被应用在深水海底管道铺设过程的计算当中,而很少会被用于浅水的铺设过程当中[5]。通过应用悬链线理论可以求出张紧器的张力以及管道各点的弯矩和轴力,通过对不同水深以及不同铺设角度的计算,可以得到相应条件下管道铺设水深与铺设角度相应的关系,为REEL型管道铺设装备的设计和选型提供重要的理论依据。
1 深水管道铺设张力计算概况
为获得铺设过程中管道的力学分析结果,起初相关研究人员曾尝试以大变形梁理论为基础,计算管道形态的解析解,但对于结果的可靠性和准确性受到很大质疑[6]。随着研究的不断深入,国内外学者应用多种方法,如:摄动法、悬链线法、有限差分法以及有限元等方法试图对管道的铺设状态进行求解。
Konuk[7]以弹性杆理论为基础,随后利用摄动法推导海底管道的静力平衡公式,并用以求解海底管道的非线性问题。黄玉盈等[8]应用异摄动法将管道内部各点分解,忽略其中的高阶项根据边界条件确定水下管道的形态。摄动法的计算效率较高,但一般适用于刚度较小的海底管道。
Dixon[9-10]为求解深水海底管道S型铺设的管道水下形态和受力情况,提出了应用悬链线理论忽略管道刚度的求解方法,其计算结果具有较高的精度和效率。龚顺风等[11]应用刚悬链线法,分析了铺设水深、管道外径以及张紧器张力对管道铺设形态的影响,提高了计算的精度。
Palmer等[12]应用有限元差分法对不同边界条件下的管道形态进行了研究,GU对方法补充了海流、海床倾角等环境因素对铺管的影响。甄国强[13]应用有限元差分法对铺设时二维管道的静力模型进行了推导,随后借助数值迭代的方法求解了管道非线性边值问题。应用该种方法对处理管道铺设的边界条件时十分适用,但其计算效率相对较低。
随着计算机技术的逐步成熟,有限元方法逐步得到了各大公司的广泛应用,Clauss等[14]考虑了不同边界条件下以及载荷分布等问题,应用有限元方法和初始值逼近的方法来求解二维管道问题。Malahy开发了适用于铺管计算的有限元软件OFFPIPE,在众多海洋工程公司得到广泛应用。
2 管道铺设形态分析
S型铺管法[15]是当前进行海底管道铺设最为常用的铺设方式,应用时间最长,使用范围最广,在进行管道铺设时,管道先在船舱内进行焊接等作业,待管道完成焊接后,管道在托架的支撑下,自然地弯成曲成“S”型曲线,亦因此得名,如图1所示。
根据管道在水下形态以及受力的不同,可以将S型铺设方式的管道分为以下四个部分:1)反弯段。在管道脱离铺管船后,以托管架为依托,管道将保持与托管架上一致的弯曲状态。当管道离开托管架并不断向下延伸时,管道的曲率将在自重及海洋载荷作用下逐渐减小。2)悬垂段。当管道继续向下延伸,其表现出自然悬链线的特性,该部分管道的曲率非常小,主要受到轴向拉力的作用。3)垂弯段。当管道延伸至海床附近,管道的曲率将再次增大,呈现出与反弯段相反的弯曲形状。管道悬链线的特性逐渐减小。4)触地段。在管道在触地之后,将在自重和铺管作用下埋入海床,同时受到海床土体对管道的抗力。
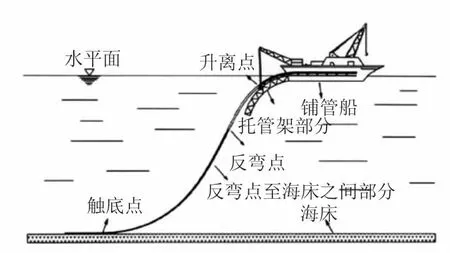
图1 S型铺管法
J型铺管法是随着人类海洋开发逐步向深海探索,为了适应铺管水深的不断增加才逐步走进各大公司视野。和S型铺管法不同,J型铺管法进行管道焊接的焊接站垂直布置,且对管道焊接工艺要求较高,这样不可避免地将影响到管道的铺设速率。在管道完成前期处理之后,凭借着对铺设塔倾角的调整和对管道张力的控制来调节管道的受力与水下形态。当进行管道铺设时,在张紧器的夹持下,管道的水下形态成“J”型曲线[17],如图2所示。

图2 J型铺管法
根据管道在水下形态以及受力的不同,可以将J型铺设方式的管道分为三个部分:1)悬垂段。在管道脱离铺设塔架,并向下延伸的管道悬于水中,这段管道受到非常小的弯矩,其曲率变化非常小,表现出明显的自然悬链线的特性。2)弯曲段。由水中段向下延伸至开进海床前的管道,由于海床土体抗力等因素的影响,边界层段受到的弯矩要比水中段管道大,所以表现明显的向下弯曲现象。3)触地段。开始于管道接触海床的位置——触地点。管道在触地段受到海床土体抗力的作用,发生管土相互作用,嵌入海床中。
REEL型铺设法作为一种新型的海底管道铺设方式,是一种在陆地预制场完成管道前期预制工作并将管道接长储存,然后由铺管船运输到指定位置进行铺设的方式。对于小管径深水管道的铺设,与S型和J型铺设法相比,卷管铺管法更为经济有效。但REEL型铺管法的铺设管径相对较小,一般从4 in到16 in不等,单层管的最大铺设直径可达16 in。REEL型铺设方式由于其在铺设管道前已将管道卷至储存卷筒,其铺设角度可通过铺设自行控制,即可在潜水区域进行作业,亦能在深水区域进行作业[18]。
3 REEL型铺设管道张力计算
在实际管道铺设过程中,管道张力是管道铺设过程十分重要的技术参数。REEL型管道铺设技术本身就具备铺设角度可调的优势,可以根据实际情况进行角度调整,以便于适应不同的施工要求。采用合理的铺设角度进行铺设对REEL型管道铺设有着十分重要的作用,一方面管道铺设张力的大小直接决定REEL型铺设核心装备的选型问题;另一方面,在适合的水深应用适合的铺设角度可以保证管道水下形态,防止管道发生过大的弯曲变形而造成屈曲。

图3 管道水下形态
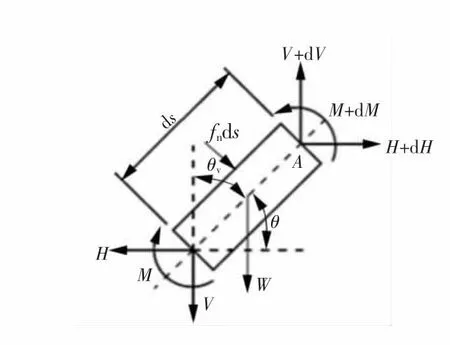
图4 管道微元受力
应用悬链线理论分析管道在深水铺设中的受力情况时,因为忽略了管道刚度的影响,可将长管道比作柔性体[20],管道张力的计算主要应用在管道水下部分,即管道与海床的接触点O和管道离开铺设塔架的释放点之间的管子悬空段,如图3所示。
如图4所示为管道微元的力平衡与几何关系,由此可以列出管道微元的平衡微分方程为
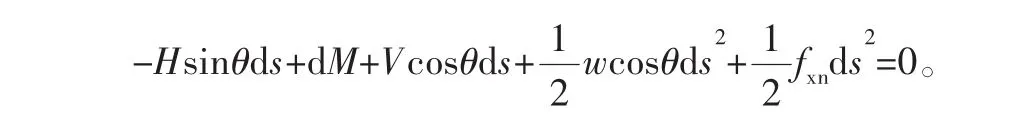
忽略海流的拖拽力,并将式中高阶项省略,可将上述方程简化为:
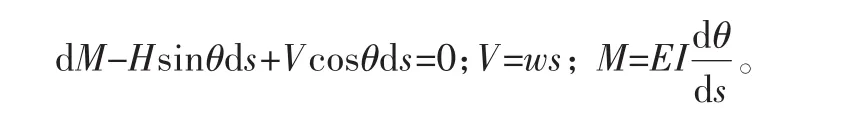
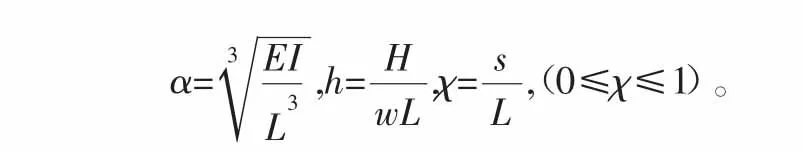
定义无量纲系数:将无量纲系数代入后可得式子:
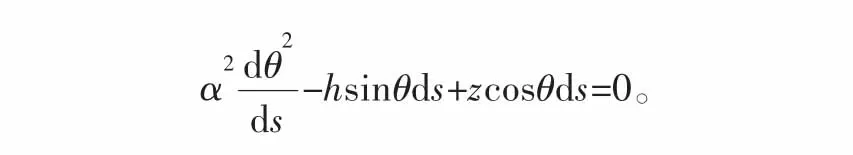
将管道的刚度影响忽略,即α2=0,可将方程进一步简化为
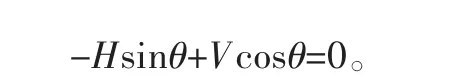
由上式可推导出管道释放点以下任意点的角度:
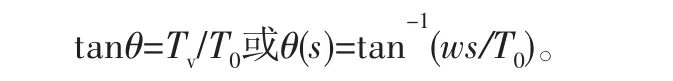
式中:T0为管道张力的水平分量;Tv为管道张力的竖直分量,Tv=ws;w为管道的浮重度;s为管线弧长;θ为杆单元与水平方向的夹角。
将管道张力的水平分量和竖直分量合成,得到管道的张力计算公式为
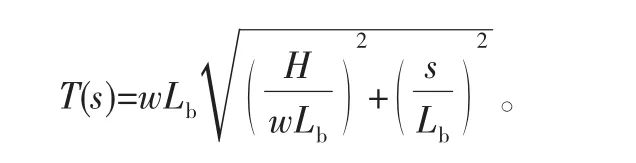
进而推导出管道的悬链线方程:
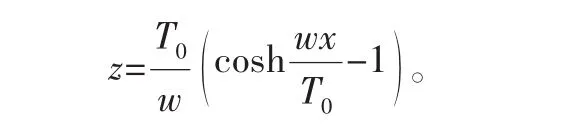
管线的水下弧段弧长s可表示为
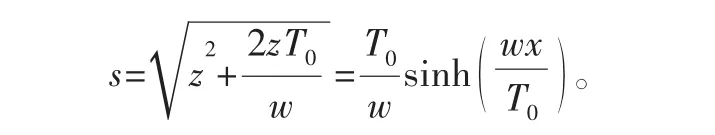
自然悬链线的弯曲可表示为
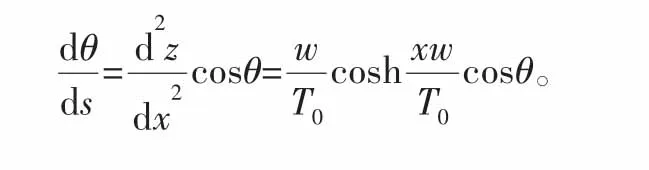
管道的最大曲率出现在管道与海床的接触点,即:

管线的曲率半径和应变的关系为
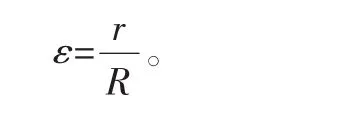
通过θ、w及z定义Tv后,代入上式可得管线轴向应力T的水平分量T0的表达式:
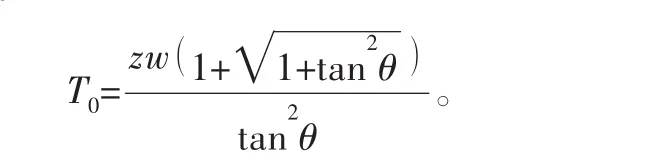
不同角度θ和水深z可以算出不同管径管道的水平分力T0,求出分力T0后,进而算得管道轴向力
4 算例分析
利用以上分析所得出的管道张力公式,将不同水深、不同铺设角度,以及不同管径的REEL型铺设相关参数代入上述公式,即可得到管道在不同水深不同入水角度进行铺设时,管道所需的张紧力。
管道整体密度可通过下式表示:
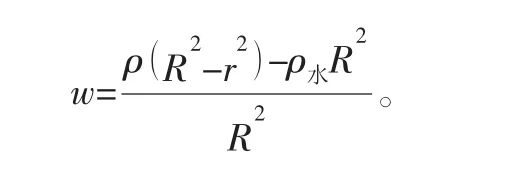
由此可以计算出2~16 in管道的浮重度,如表1所示。
以X60钢管为例,分别选取铺设水深为500、1000、1500、2000、2500、3000 m时不同管径的管道,所选管道的密度为ρ=7850 kg/m3,根据DVV相关规范选取径厚比为20的单层钢管,铺设塔角度调整范围设定为θ=50°~89.9°。
如图5所示为4 in和16 in管道在不同条件下管道张力变化曲线。
由图5可以看出:管道张力在深度相同的情况下会随着铺设角度增大而减小;在径厚比相同的情况下,各尺寸的管道张力变化曲线变化趋势相同。通过对2~16 in管道的计算分析比较可以发现,随着水深的增加,管道的最大弯矩逐渐减小,管道的轴力却逐渐增大。管道的弯矩变小可以有效地保证铺设管道发生屈曲的可能性,但轴向张力的不断增大,将会对管道铺设装备提出更高的要求。张紧力越小,海底边界层区域弯矩峰值越大。在深海区域铺管,应适当增加张紧力,这样能减少管道弯矩峰值,减少管道弯曲应力,更能保证管道的安全。

表1 不同管径对应的浮重度
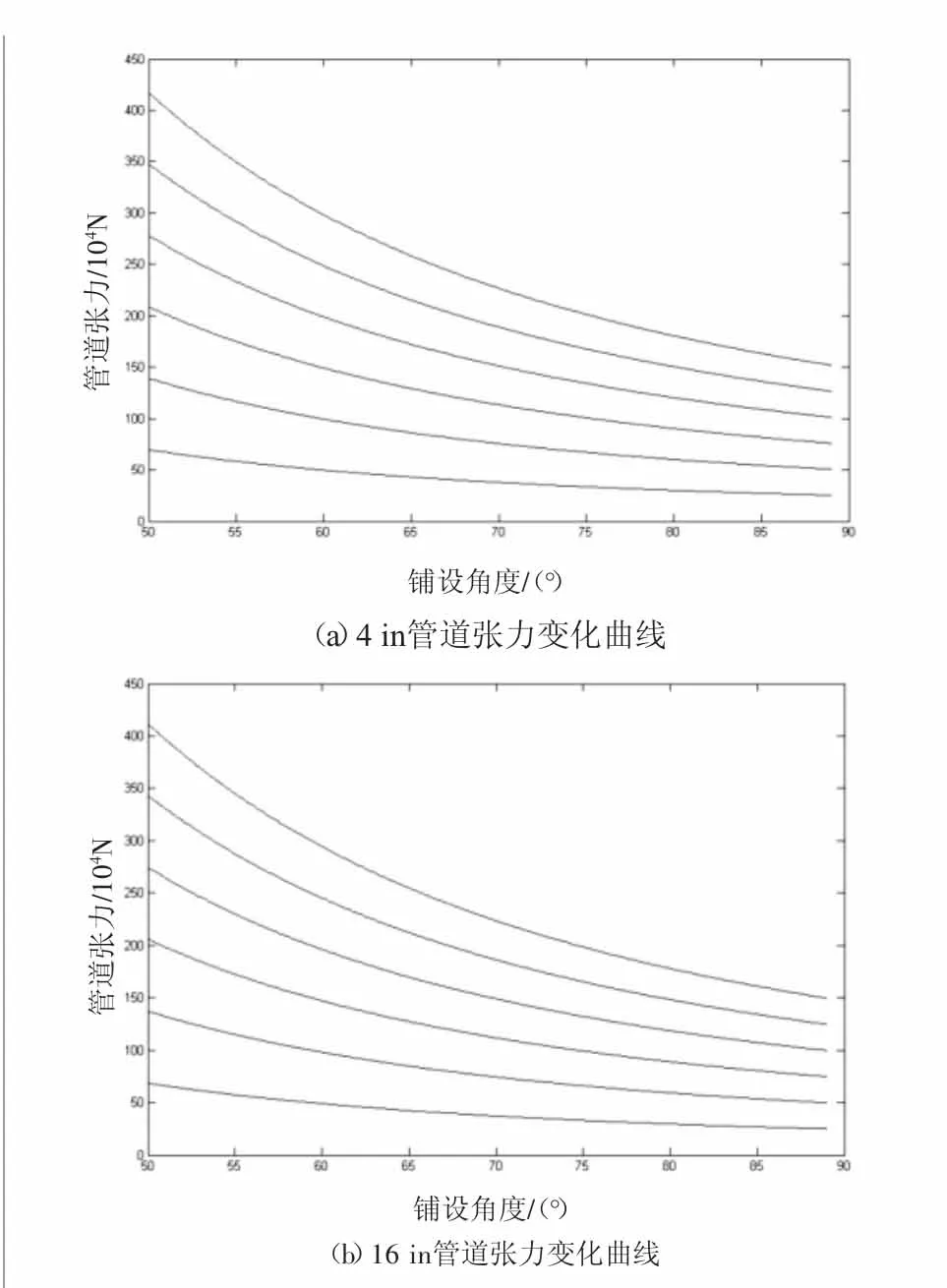
图5 管道张力曲线
5 结论
总结了国内外有关管道张力的相关计算方式,基于悬链线理论,借鉴S型管道铺设方式和J型管道铺设方式,结合REEL型管道铺设方式的实际情况,对REEL型管道铺设方式进行了管道张力计算的研究。对REEL型管道铺设方式的管道张力与铺设深度、铺设角度的关系进行了研究,对于REEL型管道铺设方式,在相同管道相同水深的条件下,其铺设角度越大,则其需要为管道提供的张力越小。对REEL型铺设装备的设备选型能够提供一定的借鉴作用,为我国REEL型铺设装备的自主研发,提供了理论依据。
