波浪作用下渗透率各向异性的海床液化分析

荣 富， 廖晨聪， 童大贵， 周香莲

(上海交通大学 土木工程系， 上海 200240)

波浪荷载会在海床表面产生周期性波浪压力，这种循环的波浪压力作用会引起海床土体内的孔隙水压力和有效应力随时间和空间而发生变化，进而导致海床土体液化失稳，对海洋建筑物的地基稳定性构成极大威胁.因此，研究波浪荷载作用下渗透率各向异性的海床液化问题，对于近海和离岸结构物的建设与设计具有重要意义.

关于波浪与海床之间相互作用的问题，自1941年Biot[1]提出Biot固结理论以来，国内外学者已开展了大量研究[2-8].Madsen[9]根据Biot固结理论，应用复变量表达式推导了线性波作用下海床土体为多孔弹性介质时位移-孔隙水压的解析解；Yamamoto等[10]利用半解析的方法求解线性推进波作用下有限或无限深度多孔弹性介质海床的动力响应；Mei等[11]采用边界层近似法进一步研究了此类问题并提出边界层理论；王栋等[12]根据二维Biot固结理论，采用有限元数值模拟的方法研究了饱和多孔弹性介质海床在线性波作用下的动力响应.从20世纪90年代开始，国内外学者对波浪导致海床液化失稳的现象进行了深入研究.Zen等[13]通过对海床动力响应的分析，探讨了波浪作用下海床的致密化机制，并对振荡孔隙水压力引起的海床瞬时液化进行分析；Sakai等[14]在分析波浪作用下海床瞬时液化时发现，利用边界层孔隙水压力的近似解能够估计波谷区海床的瞬时液化深度.20世纪初期，Lin等[15]提出三维短峰波作用下各向异性的海床动力响应模型，并用于估计波浪导致的海床液化； Suzuki 等[16]采用室内试验的方法研究了波浪作用下细砂海床的液化，并结合有限元模拟方法计算土体的最大液化深度.黄光爵等[17]在考虑振荡孔隙水压力和残余孔隙水压力的条件下推导出波浪作用下海床的最大液化深度的解析表达式.

但是，以上研究大多针对渗透率各向同性的海床的动力响应，对波浪荷载作用下渗透率各向异性的海床的动力响应及液化分析较少.Jeng等[18]考虑海床土体的各向异性，推导了波浪作用下有限深度海床动力响应的解析解；张金凤等[19]采用数值计算方法分析了在非均质各向异性海床中，土体的渗透系数对海床孔隙水压力和有效应力的影响；Wen等[20]采用有限单元法研究了不同渗透系数的2层土体在波浪荷载作用下的动力响应.

为了研究渗透率各向异性的海床的瞬态液化特性，本文采用雷诺平均Navier-Stokes(RANS)方程作为波浪的控制方程，采用动量源函数进行造波，通过LSM(Level Set Method)法对波浪的自由表面进行精确跟踪.海床响应以Biot多孔弹性方程为控制方程，并且考虑海床土体的渗透率各向异性.通过 COMSOL Multiphysics软件来实现波浪模型和海床土体模型在接触面上信息(位移、压力)的交互耦合.同时，在验证数值模型合理性的基础上，分析了波浪参数、海床的土体饱和度和渗透系数对海床瞬态最大液化深度的影响.

1 数值模型

波浪-海床相互作用的几何模型如图1所示.其中：Ls为模型的长度；d为水深；h为海床土体的厚度；F为海床表面一点.本文的数值模型包含2个模块，即波浪模型和海床模型，以准确模拟波浪与渗透率各向异性的海床的相互作用.采用RANS方程描述黏性流体流动中波浪的产生和运动，采用Biot固结理论分析海床的动力响应.波浪模型和海床模型之间采用单向耦合，即在模型计算的同一个时间步内，先以波浪模型计算所得海床表面的波浪压力作为海床模型的边界条件，以此计算海床的位移及孔隙水压力.

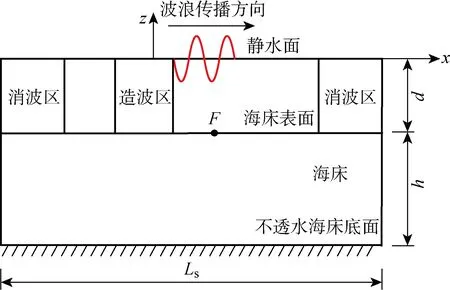
图1 波浪-海床相互作用几何模型Fig.1 Geometrical model of wave-seabed interactions

1.1 波浪模型

如图1所示，在水槽的中间部分进行数值造波，并采用LSM法追踪波浪自由液面，而在水槽的两端添加消波区.以RANS方程作为二维不可压缩流体运动的控制方程，即

μf为流体动力黏度，k为湍流动能，δij为Kronecker Delta记号，μt=ρfCuk2/ε，为湍动流体黏度，Cu=0.09，ε为湍流动能耗散率.

本文的流体力学性能模拟采用k-ε湍流模型，标准湍流模型的k方程和ε方程分别为

Gk-ρfε

(3)

(4)

式中：参数σk、σε、Cε1、和Cε2均为相关经验系数，一般取σk=1.00，σε=1.30，Cε1=1.44，Cε2=1.92.

1.2 海床模型

在建立海床模型的过程中，假设波浪荷载引起的砂质海床孔隙水渗流为层流运动，且满足达西定律，则波浪荷载将引起多孔弹性海床土体内产生超孔隙水压力，使土骨架发生变形，并服从虎克定律.本文研究渗透率各向异性的海床土体，其连续性方程为

(5)

式中：Kx与Kz分别为海床土体在x和z轴方向的渗透率；ps为波浪作用下的孔隙水压力；γw为孔隙水容重；ns为海床土体的孔隙率；us为海床土体的水平位移；ws为海床土体的竖向位移；β为孔隙水的压缩性系数，其表达式为

Sr为土体的饱和度；Ew为土体孔隙的流体体积压缩模量，其取值为Ew=2.24 GPa；pw0为绝对水压力.

(6)

(7)

(8)

海床中超孔隙水压力与有效应力的关系为

忽略惯性力，将式(6)～(8)代入(9)和(10)，所得以超孔隙水压力和位移表示的平衡微分方程为

(11)

(12)

1.3 边界条件

1.3.1海床表面 在海床表面z=-d处，土体应力相比于波浪压力可忽略不计，故设土体垂直方向的正应力和剪应力等于0，并且海床表面的波浪压力与孔隙水压力相等，即有

式中：p0为作用于海床表面的波浪压力.

1.3.2海床底面 在海床底面z=-(d+h)处，土体可视为不透水的刚性基岩，即海床土体的水平方向位移和竖直方向位移为0，故有

(15)

1.3.3海床侧边 假设在海床左右两侧边界处，土体的水平方向位移为0且为不透水边界，则有

(16)

2 模型验证

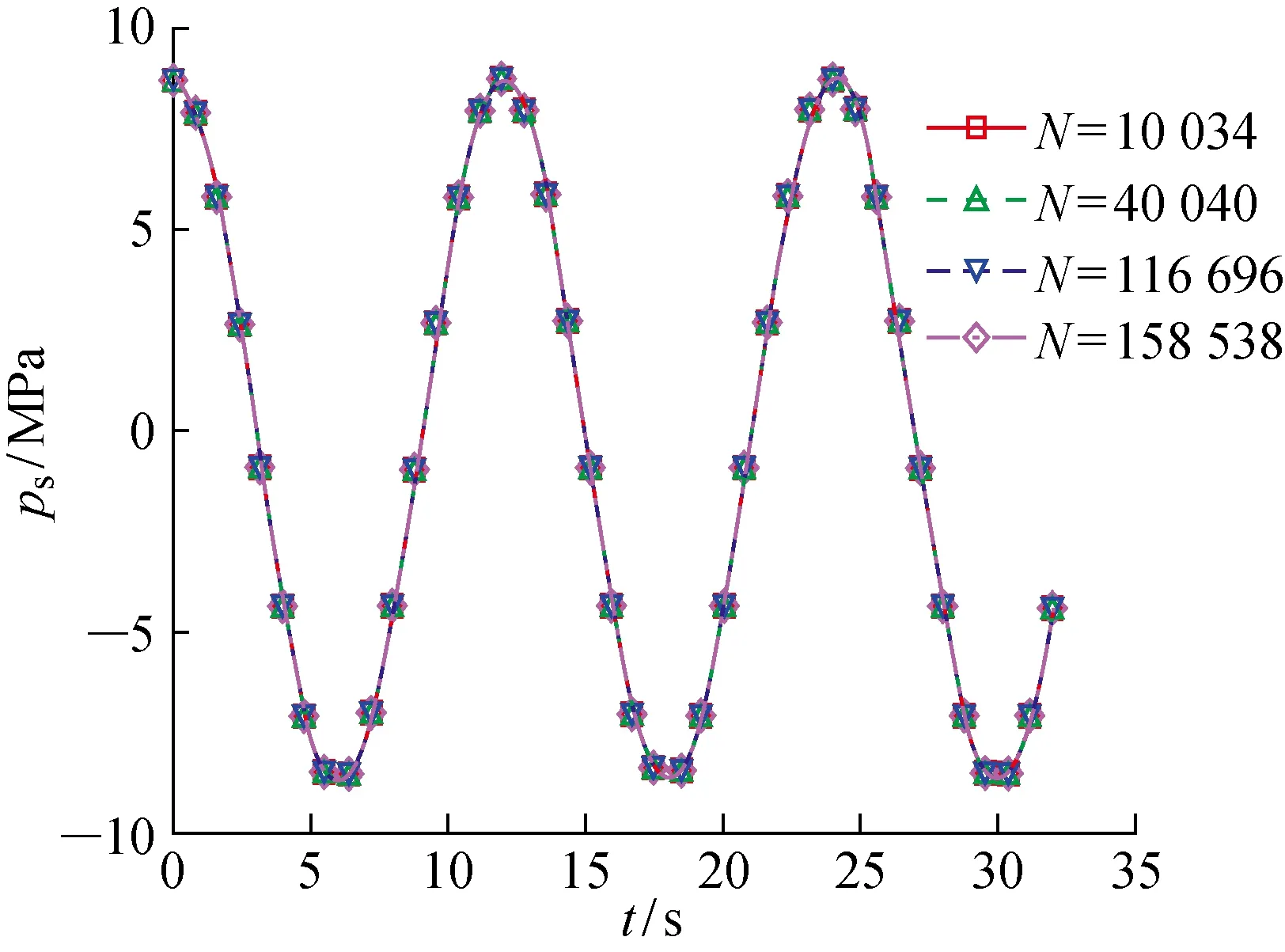
图2 不同网格数目时点F的孔隙水压力时程曲线Fig.2 Variations of pore pressure with time at point F for various mesh systems

由于渗透率各向异性的海床瞬态响应的实测数据较少，所以本文选用波浪作用下渗透率各向同性的海床动态响应的试验数据和解析结果来验证模型.首先，验证波浪模型的网格收敛性.所用波浪的相关参数分别为波浪高度H=2 m，水深d=10 m，波浪周期T=12 s；海床的相关参数分别为海床厚度h=20 m，ns=0.4，渗透系数K=1.0×10-7m/s，Sr=0.97，νs=0.333，G=0.10 MPa.图2所示为在不同网格密度下图1中模型表面点F的孔隙水压力ps的时程曲线.其中，N表示波浪模型的网格数目.由图2可见，海床表面点F的孔隙水压力不随网格数目的变化而变化，经过网格收敛性检验，确定波浪模型网格数目取N=10 034.

为验证所建立的海床模型的合理性，本文将Liu等[21]的室内模型试验值和Hsu等[22]的解析解与本文模型的数值计算结果进行比较.根据Liu等的试验设置，计算所用参数分别为H=1.23 m，T=9 s，h=1.8 m，d=5 m，G=0.127 MPa，νs=0.3，K=1.8×10-4m/s，ns=0.425，Sr=0.975，计算所得沿不同海床深度(z/h)分布的归一化孔隙水压力(|ps|/p0)如图3所示.由图3可见，3种方法所得孔隙水压力的变化趋势基本一致，且吻合较好，说明本文模型可以有效模拟波浪作用下的海床响应.

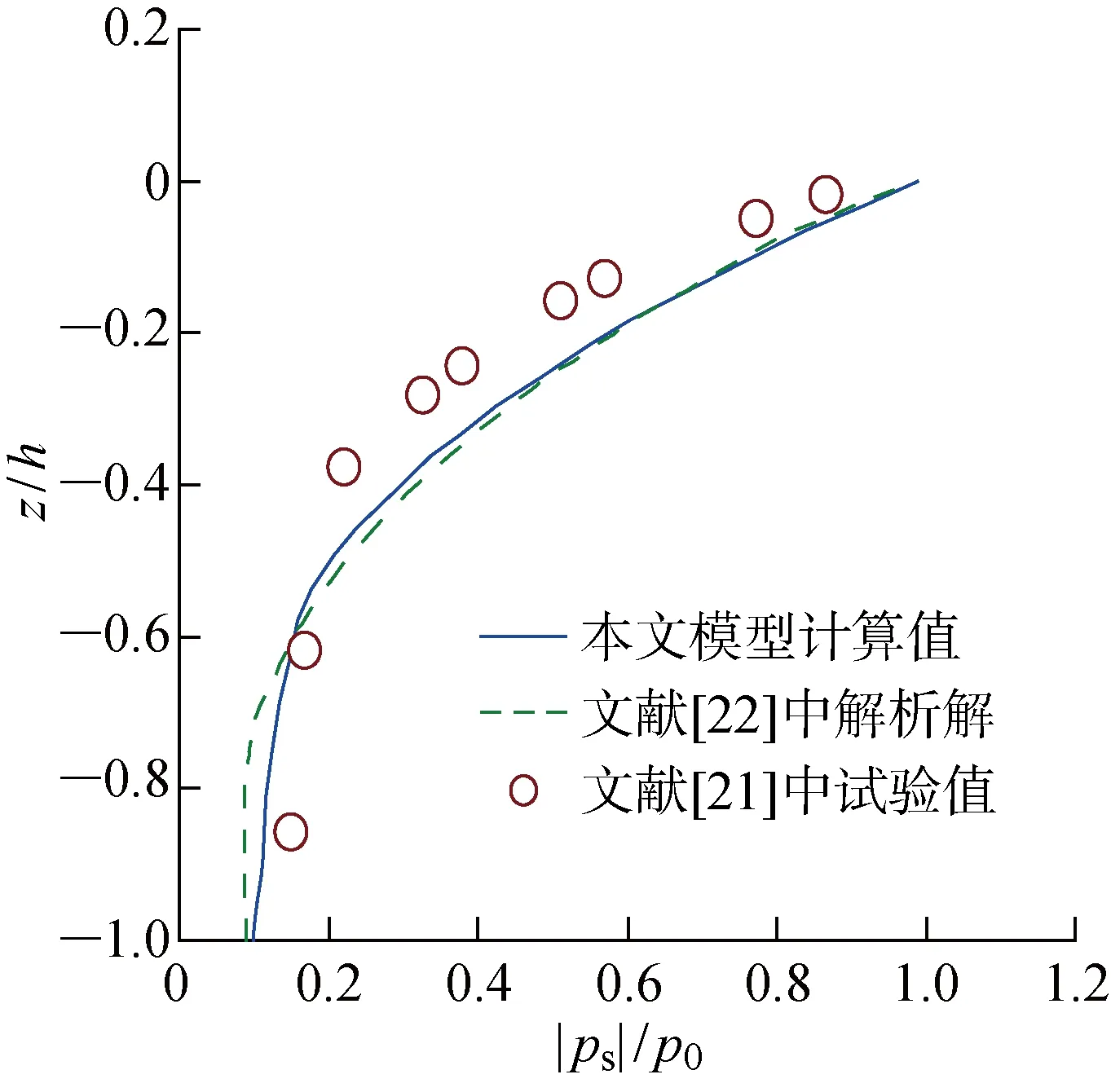
图3 沿不同海床深度分布的归一化孔隙水压力Fig.3 Vertical distributions of unified pore pressure versus seabed depth

3 海床瞬态液化分析

波浪荷载对海床作用时，波谷区水质点的向上运动会对海床产生向上的吸力.本文采用Zen等[13]提出的海床瞬态液化判别标准进行海床液化情况分析(见图4)，即

(17)

pε=|p0|-|pw|

pw为波浪作用下海床中某点的孔隙水压力.

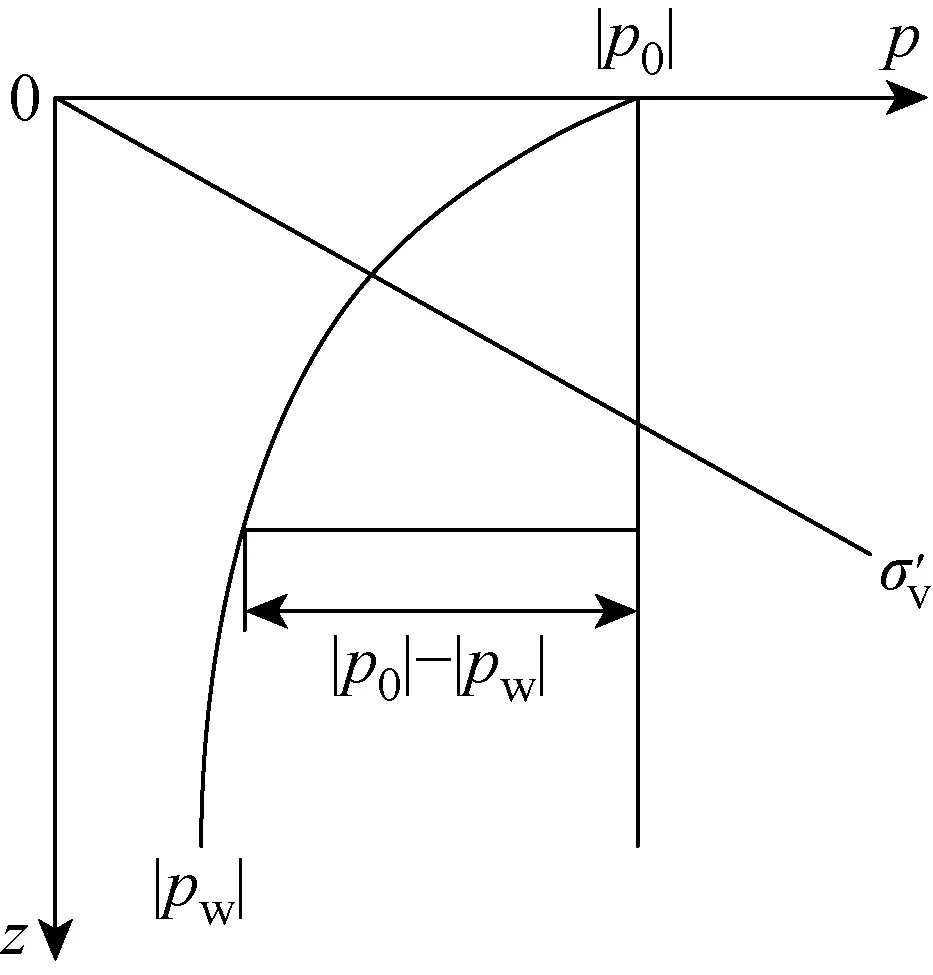
图4 海床瞬态液化判别示意图Fig.4 Schematic graph of criteria for transient seabed liquefaction

3.1 波浪参数和海床土体饱和度的影响

波浪高度直接影响波浪作用在海床表面的波浪压力，波浪周期通过影响波长而影响海床表面的波浪压力，海床土体饱和度通过影响土体的垂直孔压梯度进而影响液化深度.对于渗透率各向同性的海床，Chowdhury等[23]通过试验研究了波浪与海床相互作用下波浪周期和土体饱和度对海床液化的影响；Liu等[21]采用一维圆筒试验分析了波浪高度、波浪周期和土体饱和度对海床最大液化深度的影响.本文进一步探讨波浪高度、波浪周期以及海床土体饱和度对渗透率各向异性的海床液化情况.在研究过程中，分别选取H=2.0，3.0，4.0，5.0 m，T=10，12，14，16 s及Sr=0.95，0.96，0.97，0.98，渗透系数取Kx=1.0×10-7m/s，Kz=1.0×10-6m/s，其他参数与验证波浪模型网格收敛性时的相同.

海床瞬态最大液化深度dm随波浪高度和波浪周期的变化规律如图5(a)和(b)所示.由图可见，波浪高度和波浪周期对dm都具有显著影响.随着波浪高度、波浪周期增大，作用在海床表面的波浪压力不断增大，从而导致海床较大深度范围内的土体有效应力小于pε，渗透各向异性的海床的dm增加.结合图4可知，有效应力随海床深度增加而呈现出线性增长，而pε随海床深度的增加有限，从而使得dm的增幅逐渐减缓.图5(c)所示为不同海床土体饱和度时海床瞬态最大液化深度的变化规律.由图可见，随着海床土体饱和度增大，海床土体的垂直孔压梯度减小，从而使得dm随着土体饱和度的增加而减小，并且最大液化深度的减小速率基本保持不变.

图5 海床瞬态最大液化深度随波浪高度、波浪周期和海床土体饱和度变化的规律Fig.5 Curves of maximum liquefaction depth with wave height, wave period and saturation of soil

3.2 海床土体渗透性的影响

对于渗透率各向异性的海床， 在研究海床不同方向的渗透性对瞬态液化的影响时，分别选取Kx=1.0×10-7m/s与Kz=1.0×10-7m/s作为基准进行数值模拟，并且在分析一个方向的渗透系数对海床瞬态液化影响的过程中，固定另一个方向的渗透系数.

3.2.1垂直方向渗透系数的影响 本文在Kx=1.0×10-7m/s，Kz处于 1.0×10-6～1.0×10-2m/s的范围进行分析.数值计算结果显示，在Kz处于 1.0×10-6～1.0×10-2m/s时，海床土体的dm的变化剧烈，因此，在该范围内应尽可能得多选取一些控制点.

图6(a)～(c)分别给出了在4组不同的H、T和Sr情况下，渗透率各向异性的海床瞬态最大液化深度随着垂直方向渗透系数的变化规律.由图可见，当Kz<1.0×10-4m/s时，不同波浪条件下，dm随着Kz的变化不明显，较小的Kz使得海床中波浪所引起的浅层孔压梯度较大，导致一定厚度的海床土体发生液化.当Kz>1.0×10-4m/s时，对于H=2，3 m的海床，其波浪引起的海床土体的孔压梯度迅速减小，液化难以向海床深部发展，dm随着Kz的增大而急剧衰减；对于H=5 m的海床(如图6(a)中点A、B和C所示)，随着Kz不断增大，所对应的点A、B和C的垂直孔压梯度先增后减(见图7)，因此，dm先增后减；在不同的波浪周期和海床土体饱和度条件下，随着Kz增大，dm急剧衰减，直至为0.

3.2.2水平方向渗透系数的影响 本文在Kz=1.0×10-7m/s，Kx处于 1.0×10-6～1.0×10-3m/s的条件下进行分析.图8示出了在不同的H、T和Sr情况下，渗透率各向异性的海床瞬态最大液化深度随着Kx变化的规律.由图8(a)可见，对于不同的H，随着Kx增大，dm基本不变化.由图8(b)可见：当T=12，14，16 s时，dm随Kx的变化不显著；当T=10 s，Kx>1.0×10-5m/s时，dm随Kx增大而呈现出缓慢减小.由图8(c)可见：当Sr=0.95，0.96， 0.97 时，Kx对dm的影响不大；当Sr=0.98，Kx>1.0×10-4m/s时，dm随Kx的增大而略有减小.

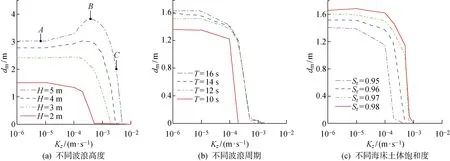
图6 海床瞬态最大液化深度随着垂直方向渗透系数的变化规律Fig.6 Curves of maximum transient liquefaction depth with vertical permeability coefficient

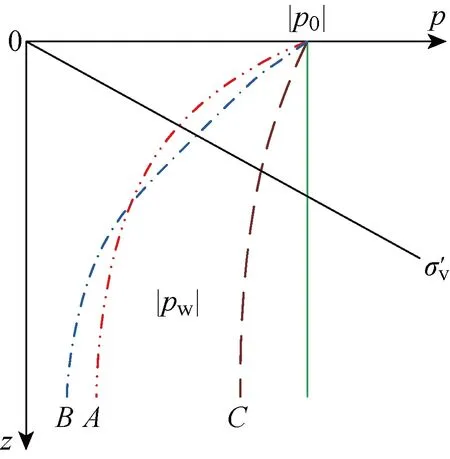
图7 不同垂直方向渗透系数下海床的孔隙水压力示意图Fig.7 Schematic graph of pore water pressure under different vertical permeabilities

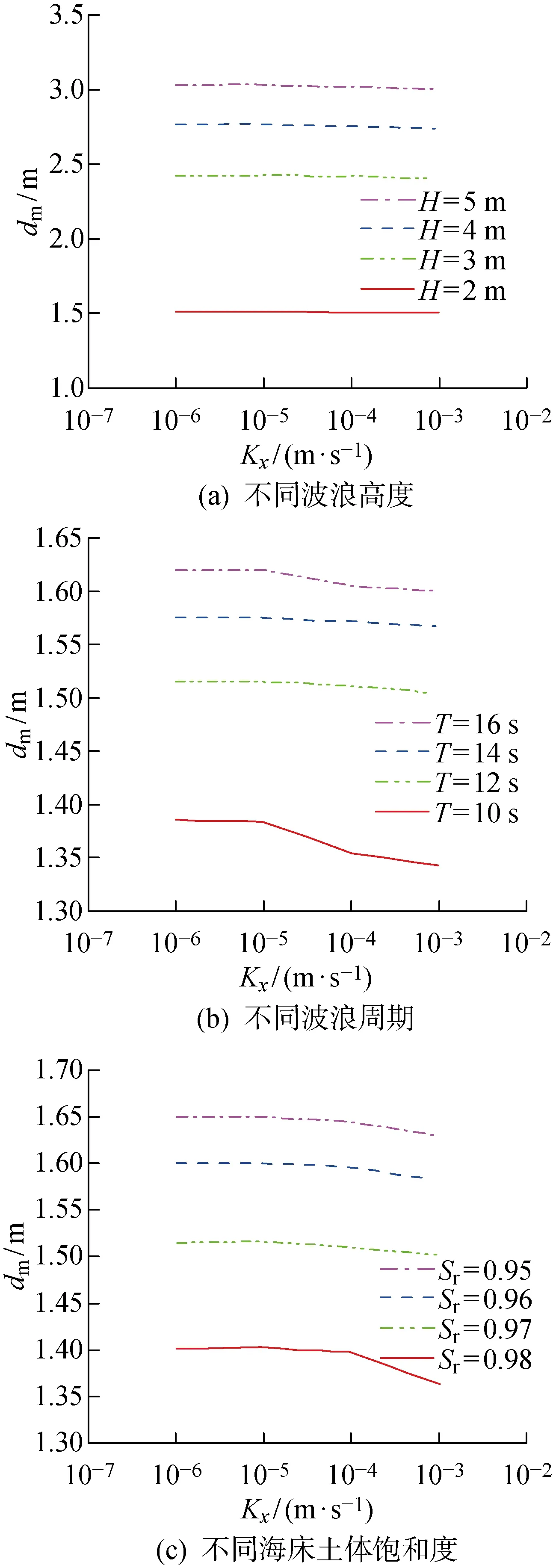
图8 海床瞬态最大液化深度随着水平方向渗透系数的变化规律Fig.8 Curves of maximum transient liquefaction depth with horizontal permeability coefficient

4 结语

(1) 所建立的波浪-海床相互作用的数值模型与以往提出的解析解和相应的室内试验结果吻合较好，从而验证了其合理性，并可以有效模拟波浪荷载作用的海床动力效应.

(2) 波浪高度、波浪周期及海床土体饱和度对渗透率各向异性的海床瞬态液化影响显著，海床的瞬态最大液化深度随着波浪高度和波浪周期的增大而增大，且其最大液化深度的增长速度都逐渐减缓；海床瞬态最大液化深度随海床土体饱和度的增大而减小，但其减小速率基本保持不变.

(3) 渗透率各向异性的海床垂直方向的渗透性对其瞬态液化影响显著.当海床土体垂直方向的渗透系数较小时，海床瞬态最大液化深度随着垂直方向的渗透系数的变化不明显；而当渗透系数增大到一定数值时，海床瞬态最大液化深度随着垂直方向的渗透系数的增大而急剧衰减.

(4) 海床水平方向的渗透系数对海床瞬态最大液化深度影响较小.