常规中蕴含新意 平淡中凸显素养*——2018年浙江省数学高考试题第22题的若干思考

●廖如舟 曾丽华 (衢州市第二中学，浙江衢州 324000)

2018年浙江省数学高考试题第22题是一道函数与导数的压轴题，具体如下:

题目已知函数

1)若 f(x)在 x=x1，x=x2(其中 x1≠x2)处导数相等，证明:f(x1)+f(x2)＞8－8ln2;

2)若 a≤3－4ln2，证明:对于任意 k＞0，直线y=kx+a与曲线y=f(x)有唯一公共点．

(2018年浙江省数学高考试题第22题)

此题主要考查函数导数、不等式等基础知识，其核心是通过导数分析函数的单调性，结合局部判断等手段得到函数的大致图像，达到“以图启数、以数论形”的目的．考查学生推理论证、分类讨论、转化化归等分析问题和解决问题的能力，能促进学生逻辑推理、数学建模、数学运算、直观想象、数据分析等数学核心素养的培养．

从阅卷的实际情况看，本题平均得分为2．5分，体现了试卷的选拔功能．但比2017年最后一题得分下降了0．5分，内容也从原来的数列不等式的考查变为了函数与导数的考查．到底是这道题本身的相对难度提升了，还是题目顺序的变换影响了学生的发挥，还是新高考后学生整体水平有所下降，值得好好分析研究，从而改进我们的课堂教学．

命题组给出了如下的参考答案:

解1)函数f(x)的导函数为

故g(x)在(256，+∞)上单调递增，因此

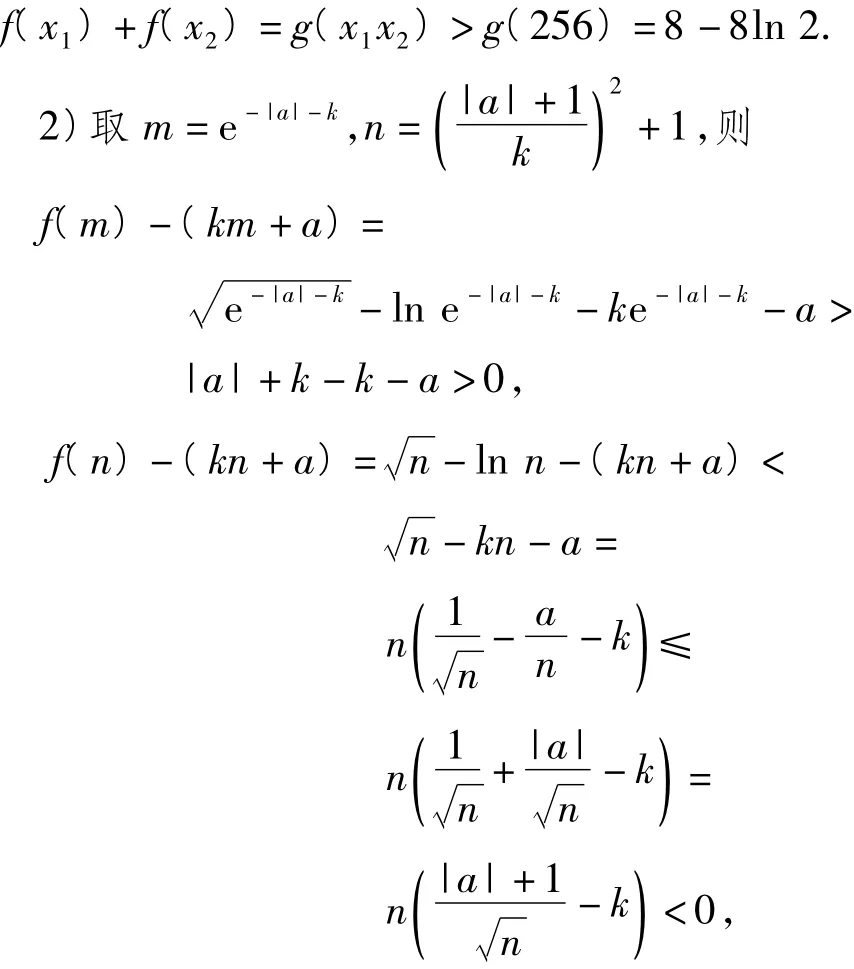
由零点存在性定理知，存在x0∈(m，n)或x0∈(n，m)，使得

因此，对于任意的a∈R，k＞0，直线y=kx+a与曲线y=f(x)有公共点．由于f(x)=kx+a，得

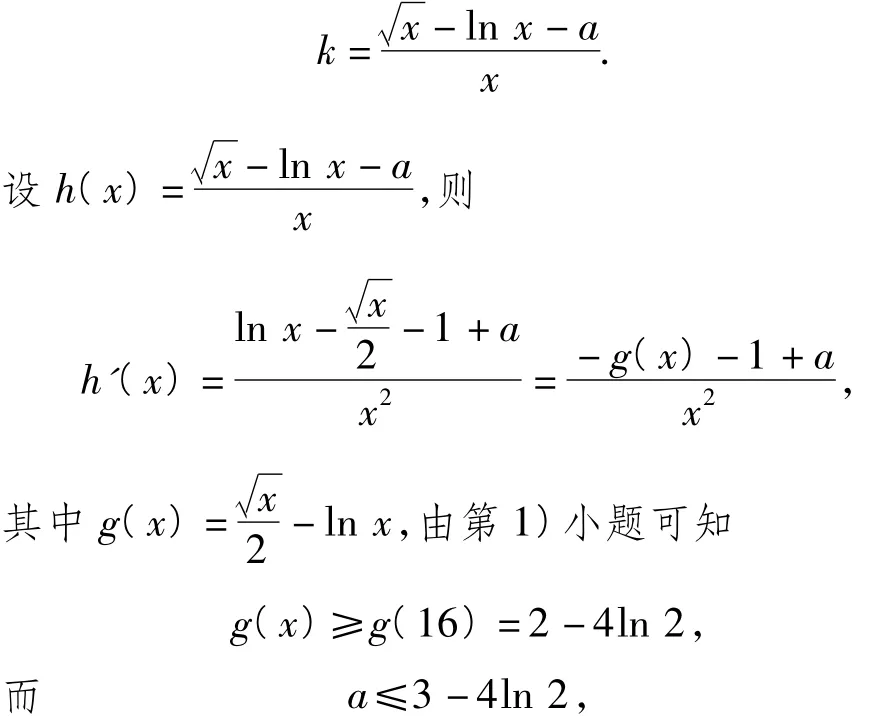
得 －g(x)－1+a≤－(2－4ln2)－1+3－4ln2=0，故h'(x)≤0，即函数h(x)在区间(0，+∞)上单调递减，因此f(x)=kx+a至多有一个实根．

综上，当a≤3－4ln2时，对于任意k＞0，直线y=kx+a与曲线y=f(x)有唯一的公共点．

对于上述解答过程，笔者有如下一些思考与感悟．

思考1对于第1)小题的解答过程，如何将双变量转化为单变量呢?

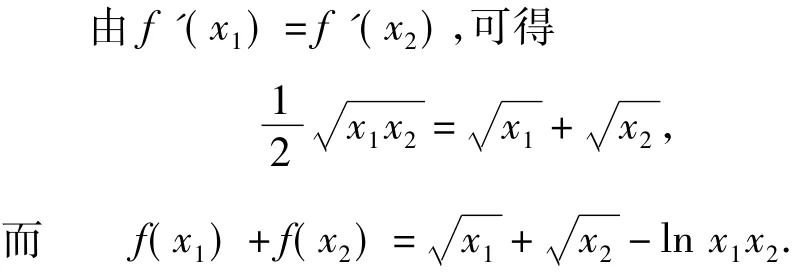
第一种角度是变量整体替换，即

由均值不等式得x1x2＞256，再由函数单调性分析可得结论．

第二种角度是变量相互替换，用x1来表示x2，得f(x1)+f(x2)=h(x1)，众所周知，这种思路非常常规，但是对于本题来说运算量较大，不建议选择．

第三种角度是变量重新转移，f'(x1)=的两个不等实根，由韦达定理得

再由 Δ=1－16m ＞0，得

第1)小题实际上是条件最值，解决条件最值问题的方法和技巧还有很多，限于篇幅，本文不再赘述．

思考2对于第2)小题的解答过程，如何寻找满足条件的m，n呢?

我们可以发现参考答案分为3个步骤:

第一步，由零点存在性定理，分析证明函数

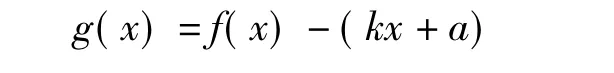
存在零点，其中证明函数存在零点是难点所在．

第二步，将函数的零点与对应方程的解联系在一起，实现参变分离，即

第三步，利用导数工具，重点研究变形函数

在a≤3－4ln2，k＞0时的单调性，从而使问题获得圆满解决．

难点分两步进行突破:

① x=e－|a|－k的来源．显然当 x越小时lnx－kx－a＞0越容易成功，因为－lnx→+∞，对于不确定符号的参数，可以利用绝对值去控制，所以只需 －lnx＞ －kx+|a|，再限定 x＜1，只需－lnx＞k+|a|，即 x≤e－|a|－k，而这个点是满足x＜1 的，故可取 x=e－|a|－k．

参考答案基于零点存在性定理和函数单调性解答问题．整个过程虽然很繁琐，但很严谨，特别是在寻找满足f(m)f(n)＜0的零点区间(m，n)时很困难．如今的课堂教学追求高效课堂，可又有多少学生能够静心思考这些问题呢?如果长期缺乏此类研究，不仅数学的严谨性有失偏颇，而且学生思维能力的发展也将受阻．

通过以上分析，不难发现找到满足f(m)f(n)＜0的零点区间(m，n)的途径一般有两种:一是利用重要不等式，如(其中x＞0)等，对原函数进行适当放缩，从而得到一个熟悉且易于求出零点的函数［1］;二是把函数拆分成熟悉的两个初等函数，画出图像，观察零点的位置，代入适当特值检验．但是学生对于(m，n)的选择会五花八门，能兼顾美观和便捷的更是少之又少，因此给阅卷带来了很大的难度．

思考3对于第2)小题，能否直接从参变分离的方法，结合直观想象，解决含参函数问题?

故 m(x)在(0，16)上单调递增，在(16，+∞)上单调递减，即

因此g'(x)≤0恒成立，g(x)单调递减．当x→0+时，g(x)→+∞，当 x→ +∞，g(x)→0+，对于任意的k＞0，g(x)=k存在唯一的实数根．故当a≤3－4ln2时，对于任意k＞0，直线y=kx+a与曲线y=f(x)有唯一公共点．

从阅卷的情况来看，采取此类做法的学生较多，但是要完整作答，需要突破两个难点:第一，需要通过二次求导的方式或不等式放缩来判断g'(x)≤0在(0，+∞)上恒成立，进而得出g(x)单调递减;第二，需要通过极限思维，判断g(x)在(0，+∞)上的图像，即当 x→0+时，g(x)→ +∞，当x→+∞时，g(x)→0+，从而判断对于任意的k＞0，都存在唯一的公共点，也可以用不等式放缩来说明g(x)在第一象限的大致图像．

思考4对于第2)小题，能否直接从分类讨论、直接求导的方法解决含参函数问题?

图1

图2

于是g(x)在(0，16)上单调递增，在(16，+∞)上单调递减，故

从而

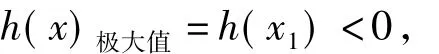
综合上述，当a≤3－4ln2时，对于任意k＞0，直线y=kx+a与曲线y=f(x)有唯一的公共点．

分类讨论直接求导的方法思路清晰，但如需完整作答，需要解决两个问题:一是对于任意k＞0，分类讨论的点在哪里?二是a≤3－4ln2的具体用处和实际控制在哪里?上述解法已经非常具体地给出了回答．分类讨论直接求导的方法对于学生的逻辑推理、数学运算这两个核心素养有很高的要求．

思考5对于第2)小题，能否充分利用数形结合思想，解决含参函数问题?

容易知道

从而 f(x)在［0，4］上下凸递减，在［4，16］上下凸递增，在［16，+∞)上上凸递增，如图3．

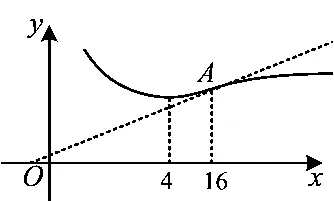
图3

故当a≤3－4ln2时，对于任意k＞0，直线y=kx+a与曲线y=f(x)有唯一的公共点．

数形结合方法的优点是简洁直观，缺点在于难把问题表述清楚．上述解答虽未“以图代证”，在证明的过程中也给出了相应的叙述，但是如需真正揭示问题的本质，即直线与曲线只有一个交点，仍需回归到之前的解法，因此本次高考阅卷过程中“思考5”中的解法并没有给满分．但是作为函数问题，以形促数，促进学生直观想象，该解法仍有其价值所在．

巧取m，n存零点，巧施图像来解析;参变分离显平凡，即使分类也时常;构造目标巧变形，终究求导堪大任;通性常法是本分，夯实基础可游刃;常规题中蕴新意，平淡问题显素养．总而言之，数学是一门研究规律的科学，在解决问题时，回归本质就是以认清数学问题的本源为基础，探寻解决问题的根本属性与规律，达到解决问题的目的．回归本质，不断挖掘数学精髓，领悟数学真谛，懂得数学价值，学会数学思维，把知识的学习和数学核心素养的培养结合起来．