基于因子图的车载INS/GNSS/OD组合导航算法

高军强, 汤霞清, 张 环, 武 萌

(陆军装甲兵学院兵器与控制系, 北京 100072)

0 引 言

随着导航技术的不断发展,多传感器组合导航已经逐渐成为各种复杂环境下长时间高精度导航的主要方式[1-2]。在陆用车载导航系统中,惯性导航系统(inertial navigation system,INS)、全球导航卫星系统(global navigation satellite system,GNSS)、里程计(odometer,OD)构成的组合导航系统被广泛应用,其中OD可以在GNSS信号因遮挡、多路径效应等因素导致不可用时,有效减缓INS的误差积累,从而实现车辆的长时间高精度稳定导航。

目前,INS/GNSS/OD组合导航算法大多以卡尔曼滤波为核心,为提高导航精度及稳定性进行了很多方面的改进。但在处理传感器异步及时延问题时,卡尔曼滤波需要采用外推内插的方法将量测统一到同一时刻,显然会引入人为误差,并增加计算负担。此外,卡尔曼滤波必须要建立组合导航系统的状态空间模型,当组合导航系统中的传感器有效性改变时,其状态空间模型就需要进行相应的调整,这无疑增加了算法设计的复杂性[3-5],也一定程度限制了使用更多有效传感器信息提高导航性能的可能性。

因子图是概率图模型的一种,其对导航状态量与导航系统测量值之间的概率关系进行编码,将状态量定义为变量节点,各传感器测量值定义为因子节点,多传感器组合导航便转换为在因子图中相应的变量节点上连接这些因子节点[6-7]。因子图模型具有很强的灵活性,能够实现传感器的即插即用,已经在导航领域受到广泛关注[8-10]。

本文将基于因子图的组合导航算法应用于车载INS/GNSS/OD系统中,构建了组合导航系统因子图模型,推导了因子图增量推理方法,并对其在处理传感器有效性动态改变、传感器存在异步和时延等方面的性能进行了深入研究。

1 组合导航系统因子图模型

以INS因子图模型为主体,当GNSS、OD等传感器测量信息有效时,将与之对应的因子节点连接进INS因子图模型中,构成组合导航系统因子图模型。

1.1 INS因子图模型

INS性能极大地依赖于惯性测量单元(inertial measurement unit,IMU)对载体运动状态的高频测量,该频率一般远高于导航系统的输出频率,即相对于导航系统输出而言,INS测量数据存在大量冗余信息。因此,在建立INS因子图模型时,可以采用智能因子的思想[11],仅将需要输出的状态量添加为变量节点,相邻两变量节点对应时刻之间的IMU测量数据进行综合,定义智能因子节点,从而降低因子节点的更新频率,提高算法实时性。

图1所示为INS因子图模型构建方案。根据实际系统应用需求确定导航状态量输出频率,进而决定智能因子更新周期,并将需要输出的导航状态量定义为目标变量,在因子图中添加变量节点。为了对IMU中惯性传感器测量误差进行修正,将惯性传感器偏差变量也添加到变量节点中,并根据偏差传播函数定义偏差因子节点。对一个更新周期内的IMU测量数据,采用预积分和INS解算分别建立预积分因子节点和解算结果因子节点,连接到因子图中对应的变量节点上。

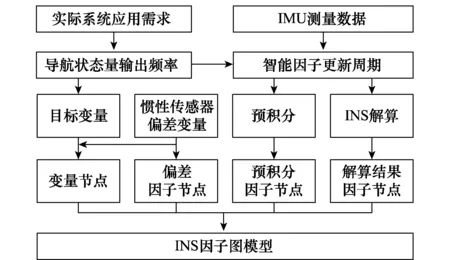
图1 INS因子图模型构建方案Fig.1 Construct scheme of INS factor graph model

INS通过对加速度、角速度测量值进行积分,得到载体的位置、速度、姿态信息,是一种航位推算系统。在建立智能因子节点时,可以采用预积分方法对一个更新周期内的IMU测量数据进行综合。组合导航系统中,INS初始对准可以在其他导航方式的辅助下快速完成,以获得载体的初始位置、速度、姿态信息。然后,将加速度、角速度测量值直接在载体系下进行预积分,可以极大地降低计算量,提高算法实时性[12]。

设导航状态量输出时刻为tk,k=0,1,…,则智能因子更新周期T=tk+1-tk。对一个更新周期tk～tk+1内的IMU测量数据在tk时刻载体系下进行预积分,得到位置、速度、姿态增量的计算公式为

(1)

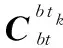
根据INS航位推算的原理,可进一步得到tk+1时刻载体位置、速度、姿态为

(2)

式中,gn表示重力矢量。

式(2)即为INS系统状态方程离散形式,可以统一表示为

,αk,zk)

(3)

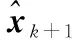
,xk,αk)d(xk+1-h(xk,αk,zk))

(4)

在运动过程中,载体姿态是时刻变化的,而一个智能因子更新周期内的IMU测量数据全部在tk时刻载体系下进行预积分,实际上是一种简化处理方式,尤其当载体姿态变化较快时会产生比较大的误差。鉴于此,在进行预积分的同时,采用经典INS处理方式对一个更新周期内的IMU测量数据进行解算,解算方法[4]不再赘述。在对tk～tk+1内的IMU测量数据进行解算时,tk时刻的位置、速度、姿态可以由组合导航的结果中得到,每次解算时间长度仅为一个更新周期,从而避免出现过大的误差积累,保证了解算结果的精度。

(5)

惯性器件偏差随时间不断变化,假设其转移函数为

αk)

(6)

则偏差因子节点定义为

αk+1,αk)d(αk+1-g(αk))

(7)

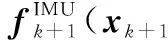
图2 INS因子图模型Fig.2 Factor graph model of INS

1.2 GNSS因子节点

GNSS可以提供载体的位置及速度信息,其测量方程表示为

(8)

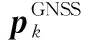
(9)

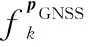
1.3 OD因子节点

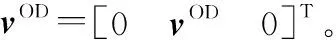
令nOD表示OD测量噪声,则OD测量方程可以表示为

(10)

从而得到OD因子节点为

(11)

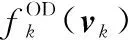
1.4 INS/GNSS/OD因子图模型

当GNSS、OD测量频率与系统输出频率相同且完全同步时,每一个导航状态量输出时刻都存在GNSS和OD测量值,将GNSS因子节点、OD因子节点连接到INS因子图模型中,即可得到INS/GNSS/OD因子图模型,如图3(a)所示。

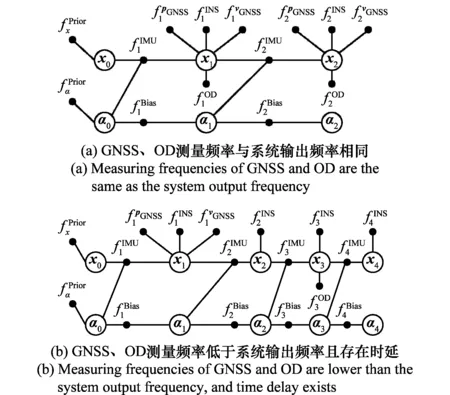
图3 INS/GNSS/OD因子图模型Fig.3 Factor graph model of INS/GNSS/OD

当GNSS、OD测量频率与系统输出频率不同,以及存在时延时,只需要将tk时刻接收到的GNSS或OD测量值定义为因子节点,连接到INS因子图模型中。图3(b)所示INS/GNSS/OD因子图模型便是由于GNSS、OD测量频率低于系统输出频率且存在时延得到的。

上述构建组合导航系统因子图模型的过程表明,组合导航系统中各传感器的因子节点在因子图模型中是相互独立的、互不影响的。以GNSS的有效性改变为例,当GNSS突然失效时,只需要抑制GNSS因子节点的继续添加,便转换为INS/OD因子图模型;而当GNSS变为有效时,只需要重新添加GNSS因子节点,便恢复为INS/GNSS/OD因子图模型。说明采用因子图模型描述组合导航问题可以灵活地处理传感器有效性的动态改变,基于因子图的组合导航算法具有很强的扩展性和灵活性。

2 组合导航因子图模型推理方法

因子图模型将组合导航中对状态量极大后验估计值的求解转化为了对因子图的推理。因子图推理的基本算法是和积算法[13],在实际工程应用中各种精确推理或近似推理方法被提出,并取得了较好的效果[14]。考虑到导航系统需要具备很强的实时性,而组合导航因子图模型又是一个随时间不断递增的动态图模型,故宜采用增量推理技术[15]。

2.1 因子图算法

因子图模型中,变量节点集合表示为X;因子节点集合表示为F;连接节点的所有边构成集合E,则因子图可以表示为

G=(F,X,E)

(12)

根据因子图理论,因子图G描述了对函数f(X)的因式分解,表示为

(13)

式中,Xi表示与因子节点fi相连的变量节点集合,Xi⊆X。

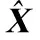
(14)

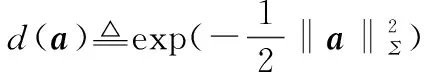
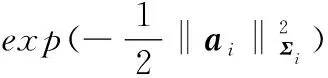
(15)

因此,对式(13)取极大值等价于最小二乘问题,即

(16)

2.2 增量推理方法

因子图模型随时间的不断递增直观的表现为X中的变量越来越多,如果每一次进行因子图推理都对X中的所有变量重新求解最优估计值,显然是无法满足系统实时性需求的。下面以图2所示因子图模型为例详述因子图模型增量推理方法。

图2(a)所示t1时刻因子图模型对应的雅克比矩阵为Jt1。采用变量消除算法[16]按照x0→α0→x1→α1的顺序进行消除,得到贝叶斯网络如图4(a)所示,对应的平方根信息矩阵是对Jt1进行QR分解得到的上三角矩阵Rt1。由于通过消除算法得到的贝叶斯网络是弦图,因此可以将其表示为贝叶斯树的形式,如图4(b)所示。

x0α0x1α1x0α0x1α1

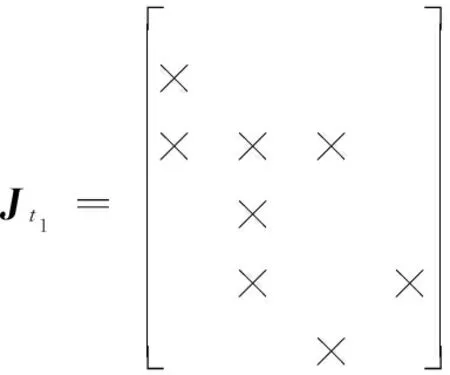
(17)

式中,×表示矩阵中的非零元素。

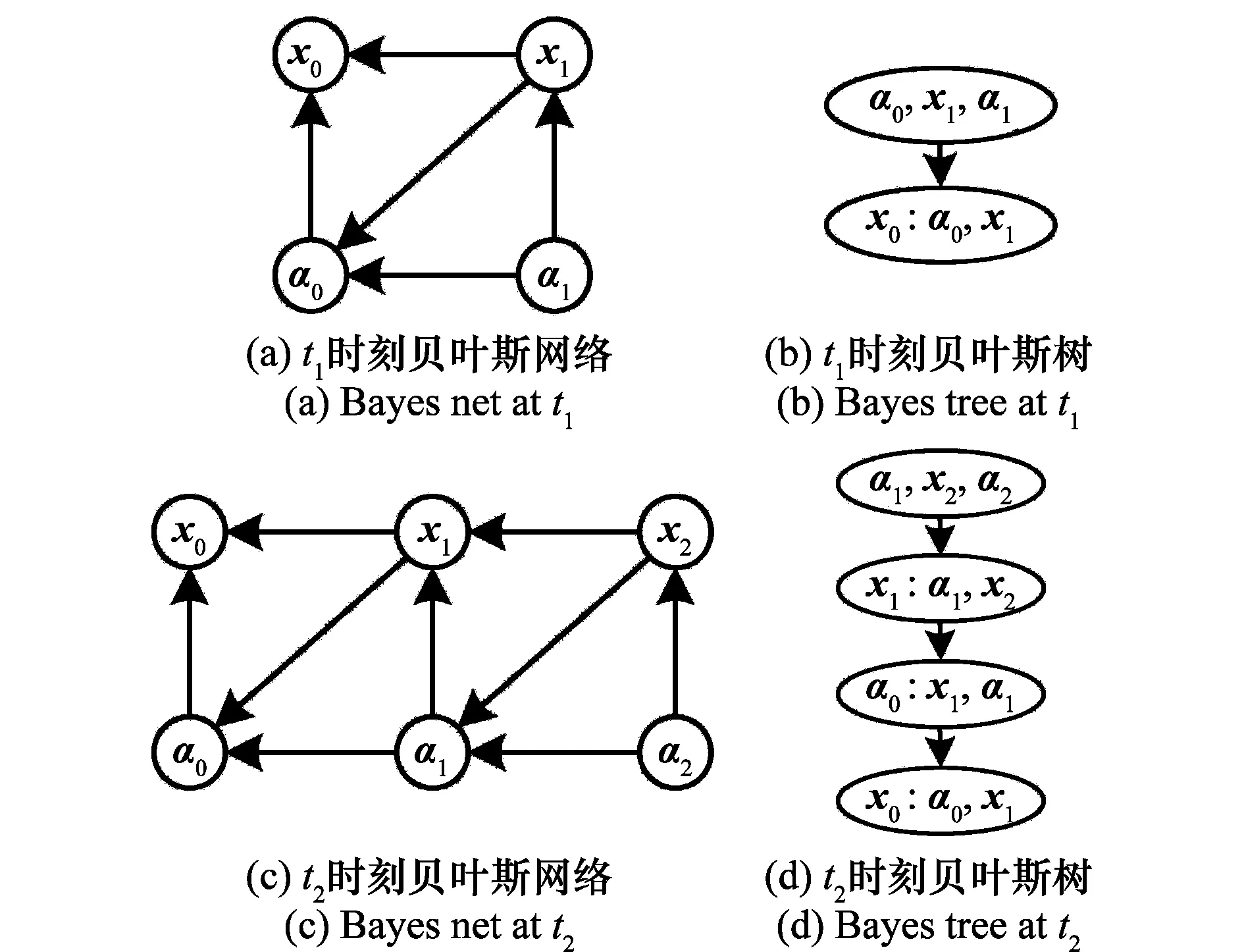
图4 贝叶斯网络和贝叶斯树Fig.4 Bayes net and Bayes tree

对比发现,加入新的节点,仅对部分状态变量的估计产生影响,因此在当前时刻的推理中只需要对受到影响的部分状态变量及新添加的状态变量进行估计。

(18)

当因子图中加入新的因子节点时,首先根据新因子节点中包含的状态量确定贝叶斯树中受影响的部分以及涉及到的状态量,原因子图中包含这些状态量的部分与新因子节点构成新的因子图,然后转化为新的贝叶斯树,再与未受影响的部分相接,从而实现贝叶斯树的增量更新。

3 仿真分析

在Matlab环境下,进行仿真分析,仿真条件设置如下:

(1)仿真轨迹起始位置为纬度39°、经度116°、海拔35 m,初始速度为0,航向正北,经加速、转弯、爬坡、下坡、减速等动作后到达终点为纬度39.02°,经度115.85°,海拔48 m,途中最大速度为20 m/s,最高海拔为230 m,总行驶时间为1 800 s；

(2) INS中陀螺的常值漂移为0.02 (°)/h、随机漂移为0.01 (°)/h,加速度计的常值零偏为100 μg,随机零偏为50 μg；

(3)GNSS的经度、纬度测量噪声均方差为1 m,高度测量噪声均方差为3 m,3个方向速度测量噪声均方差都为0.1 m/s；

(4)OD输出脉冲经刻度因子转化为速度,噪声均方差为0.2 m/s；

(5)INS采样频率为100 Hz,GNSS更新频率为1 Hz,OD输出频率为1 Hz。

3.1 传感器有效性动态改变仿真

假定系统输出频率与GNSS、OD测量频率相同且完全同步,仿真过程中设置部分时段GNSS数据不可用,检验因子图算法处理传感器有效性动态改变的能力。3次仿真实验的具体设置如下:

实验1GNSS数据始终可用;

实验2GNSS信号在600～1 200 s不可用,INS单独导航;

实验3GNSS信号在600～1 200 s不可用,采用OD辅助INS进行导航。

图5(a)、图5(b)、图5(c)所示分别为3次仿真实验得到的经度、纬度、高度误差曲线。结果表明,实验1得到的位置误差最小,实验3次之,实验2误差最大。

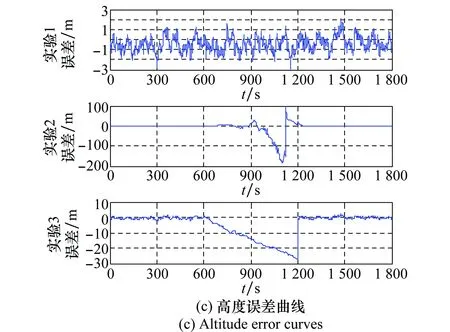
图5 实验1、2、3位置误差曲线对比Fig.5 Comparison of position error curves of test 1, 2, and 3

实验1中,GNSS数据始终可用,组合导航系统一直处于INS/GNSS工作模式,达到了很高的位置精度。

实验2中,GNSS信号在600～1 200 s不可用,组合导航系统中传感器有效性先后发生了两次改变。当GNSS信号在600 s失效时,组合导航系统由INS/GNSS工作模式切换为INS单独导航模式,因子图模型中抑制了因子节点fpGNSS和fvGNSS的添加,位置误差由于INS得不到修正而迅速积累。当GNSS信号在1 200 s重新有效后,组合导航系统由INS单独导航模式切换为INS/GNSS工作模式,因子节点fpGNSS和fvGNSS又被添加进了因子图中,位置误差得到修正。

实验3中,组合导航系统中传感器有效性也发生了两次改变。当GNSS信号在600 s失效时,在抑制因子节点fpGNSS和fvGNSS的添加的同时,加入了因子节点fOD,系统由INS/GNSS工作模式切换为INS/OD工作模式。当GNSS信号在1 200 s时重新有效后,因子节点fpGNSS和fvGNSS又被添加进了因子图中,同时抑制因子节点fOD的添加,系统由INS/OD工作模式恢复为INS/GNSS工作模式,INS误差被迅速修正。相较于实验2,当GNSS信号不可用时,OD的引入有效缓解了INS的误差积累速度。

根据以上分析,INS/GNSS/OD组合导航系统有INS/GNSS、INS、INS/OD 3种工作模式。当系统由于传感器有效性改变而在这3种工作模式之间切换时,只需要在因子图模型中抑制失效传感器的因子节点,或接入新的有效传感器的因子节点,不需要对因子图模型进行更多的调整,从而保证了组合导航系统在各种工作模式下的无缝切换,使得系统具有很强的鲁棒性。

3.2 传感器异步和时延仿真

假定INS/GNSS/OD组合导航系统中所有传感器的测量信息均稳定有效,设置GNSS、OD的测量频率与组合导航系统输出频率存在异步和时延的情况,检验因子图算法处理传感器异步和时延的能力。3次仿真实验具体设置如下:

实验4无异步、无时延;

实验5有异步、无时延;

实验6有异步、有时延。

其中,“有异步”是指系统输出频率为5 Hz,而GNSS、OD测量频率为1 Hz;“有时延”是指GNSS与OD数据更新时刻相对于系统输出整点时刻分别存在0.2 s和0.6 s的时延,如图6所示。

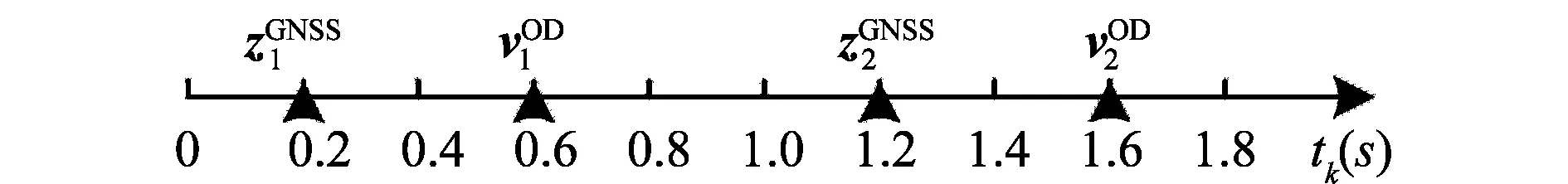
图6 传感器异步及时延Fig.6 Asynchronization and time delay of the sensors

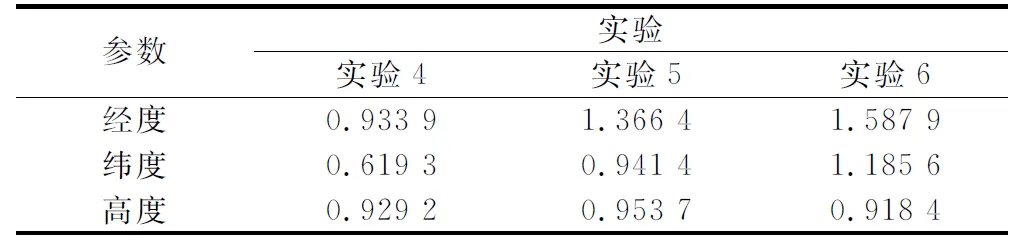
图7所示为3次仿真实验得到的位置误差曲线,表1所示为位置误差均方根(root mean squared,RMS)对比。整体而言,3次仿真实验的位置误差基本处于同一水平,当存在异步和时延时,位置误差出现了一定程度的增大。这主要是由于系统输出频率高于GNSS、OD测量频率,在没有GNSS、OD数据的时刻,只能单独依赖INS。而对于因子图算法而言,其完全不需要针对传感器异步和时延进行调整,只需要按部就班地将接收到的传感器测量值定义为因子节点连接到因子图中对应的变量节点上,然后采用增量推理算法对因子图进行推理,便可以得到导航状态量的最优估计值。

图7 实验4、5、6位置误差曲线对比Fig.7 Comparison of position error curves of test 4, 5, and 6

4 结 论

本文提出了基于因子图的INS/GNSS/OD组合导航算法,研究其处理传感器有效性动态改变、传感器存在异步和时延等方面的性能。实验结果表明,当传感器有效性发生变化时,只需要在因子图模型中抑制或加入其因子节点,便可以完成组合导航系统工作模式的无缝切换,使系统具有很强的鲁棒性。而对于传感器存在异步和时延的情况,因子图算法只需要直接将接收到的传感器测量值定义为因子节点连接到因子图中对应的变量节点上,不需要将不同传感器测量值统一到同一时刻,从而避免引入额外的人为误差。

因子图模型良好的扩展性和灵活性,使其在处理多传感器组合导航问题中具有较大优势。基于因子图的INS/GNSS/OD组合导航算法对于其他应用环境下的多传感器组合导航系统具有较高的参考价值。