基于参数优化的导弹编队控制一致性算法

黄 伟, 徐建城, 吴华兴, 李俊兵

(1. 空军工程大学航空航天工程学院, 陕西 西安 710038; 2. 西北工业大学电子信息学院, 陕西 西安 710072)

0 引 言

导弹协同编队是未来局部战争的主战模式,各军事强国都不遗余力的开展相关技术的研究工作[1-2],导弹编队控制的主要任务是有效地生成和保持预定的编队几何形态,韦常柱[3]等采用小扰动线性化方法设计了导弹编队保持控制器;穆晓敏[4]等建立了由编队队形控制及编队离入队管理等模块组成的编队控制系统;周慧波[5]等将编队控制问题转化为跟踪问题,所提出的制导律算法具有一定的鲁棒性。以上成果主要基于单枚从弹与领弹的相对位置关系,未将导弹编队作为整体考虑,各枚从弹控制算法的收敛时间存在较大差异,不适用于大规模导弹编队的队形控制。近些年来,一致性算法[6-7]成为解决大规模编队控制问题的有效方法,林志云[8]等基于相对坐标系,应用图拉普拉斯方法建立了队形控制一致性算法;文献[9-10]提出基于二阶运动学模型的飞行器编队一致性算法,并将虚拟结构法、领从法、行为法等标准化在一致性算法框架内。然而,以上基于一致性理论的编队控制算法在设计过程中均假设导弹自动驾驶仪是非惯性系统,无迟滞的响应由制导系统生成的制导指令。实际中,外环制导回路生成的制导指令是通过内环自动驾驶仪实现的,受自动驾驶仪动态特性的影响[11-12],可能导致控制算法的发散,影响编队闭环系统的稳定性;其次,现有一致性算法中的参数仅限定了其取值范围,未经参数优化过程,不能实现在某种性能指标下的编队最优控制。

鉴于此,针对领从结构导弹编队队形控制问题,提出一种基于参数优化并考虑自动驾驶仪动态特性的一致性编队控制算法。首先,将导弹自动驾驶仪等效为一阶惯性环节,基于坐标变换得到了制导指令与所需控制力的关系模型;其次,建立了导弹编队一致性控制算法,构建了编队闭环制导控制系统方程,应用代数图论证明了闭环系统的稳定性;最后,以编队各成员位置和速度的累计误差建立指标泛函,基于最优控制提出了算法中待定系数的优化方法,从而进一步提高了导弹编队系统的性能。

1 导弹编队相对运动模型的建立

为便于描述导弹编队相对运动关系,选取地面某点为坐标原点建立地理坐标系(OXYZ)e,如图1所示。导弹编队由1枚领弹和2枚从弹组成。编队过程中,要求各枚从弹在制导控制系统的作用下与领弹生成并保持既定的相对位置关系和速度关系。

图1 导弹编队示意Fig.1 Missile formation in 3D space

将导弹简化为质点,并仅考虑导弹的弹道倾角和弹道偏角,导弹所需的控制力矢量F=[FxFyFz]T定义在以导弹质心为原点、以速度矢量方向为X轴向的弹道坐标系(OXYZ)m中,其分量分别为导弹轴向、俯仰方向和偏航方向的控制力。由此,导弹在三维空间中的运动可描述为

(1)

图2 导弹制导控制系统Fig.2 Control system of missile guidance

如图2所示,根据编队指标要求,假设控制器输出的制导指令为Vd=[VexdVeydVezd]T,即地理坐标系中3个轴向的理想速度,导弹控制系统响应制导指令,计算所需的控制力矢量F,从而控制导弹的飞行状态。总体设计阶段,导弹自动驾驶仪可以等效为一阶惯性环节，即

(2)

式中,V=[vxvyvz]T表示导弹在地理坐标系中飞行速度矢量;τ为等效环节时间常数;s为拉普拉斯算子。式(2)的微分方程形式为

(3)

式中,各项运动参数均定义在地理坐标系下,而导弹控制力矢量F定义在弹道坐标系下,为了建立F与Vd之间的关系式,通过坐标变换,可得地理坐标系下控制力矢量Fe与F之间的变换式为

(4)

式中,Tem为弹道坐标系到地理坐标系的转换矩阵,由此可得

(5)

再由式(3)可得导弹控制力F与制导指令Vd之间的关系式为

(6)

由式(6)可知,根据导弹制导系统计算得到的Vd,控制系统即可得到所需的控制力矢量F,在导弹编队过程中,设计满足编队要求的控制算法,得到制导指令Vd是编队控制的关键。

2 导弹编队控制一致性算法

2.1 编队控制算法的建立

领从结构导弹编队过程中,领弹一般配置有高性能通信和探测装置[13],实现对远距离目标的探测,其运动状态不受从弹的影响。由此,控制算法的设计目标为:得到编队各从弹的制导指令Vd,使编队各成员趋于理想位置的同时,速度与领弹趋于一致。基于一致性理论,所设计的从弹i制导控制算法式为

(7)

结合导弹自动驾驶仪等效式(3),可得从弹i闭环制导控制系统方程为

(8)

(9)

将导弹编队作为整体考虑,应用代数图论知识,编队闭环制导控制系统方程矩阵形式为

(10)

定理1导弹编队各成员在控制算法式(7)的作用下,若参数γ的取值满足下式，即

可保证式(10)所表示的编队闭环制导控制系统方程的收敛,即各枚导弹趋于理想位置的同时,速度趋于一致。

证明式(10)是齐次线性方程标准形式,其解

(11)

将矩阵Σ写为Jordan型Σ=SJS-1,即

exp(Σt)=Sexp(Jt)S-1

(12)

矩阵Σ的特征方程为

det(λI2n-Σ)=det((λ2+τ-1λ+γ)In+(τ-1λ+γ)L)

(13)

负拉普拉斯矩阵-L的特征方程为

(14)

式中,μi是-L的第i个特征值,将式(13)重写为

det(λI2n-Σ)=

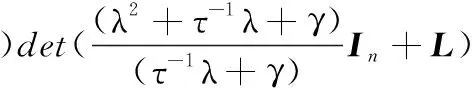
(15)

比较式(14)和式(15),式(13)的根可求解为

λ2+τ-1(1-μi)λ+γ(1-μi)=0

(16)

则矩阵Σ的特征值为

(17)

根据普拉斯矩阵L的性质,有Re(μi)≤0,则Re(μi-1)<0。令ηi=μi-1,根据复数辐角缩放原理[10],当γ的取值满足下式时，即

(18)

式(16)的所有根具有负实部,即Re(λ)<0,由式(11)和式(12)可得

(19)

即式(10)收敛,从而保证位置误差和速度误差趋于零,即

(20)

证毕

2.2 控制算法的参数优化

将导弹编队控制算法的设计过程描述为最优控制问题,在假设导弹自动驾驶仪为一阶惯性环节的前提下,式(3)所描述的系统状态方程标准形式为

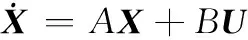
(21)

式中,X=V;A=-τ-1;U=Vd;B=τ-1。在控制算法式(7)的作用下,闭环编队制导控制系统方程形如式(10),其收敛性得到了证明。然而,式(7)仅给出了控制算法的结构,其中还包含待定系数γ,式(18)给出了保证算法收敛时,γ的取值范围。本节对待定系数γ进一步优化,使之在某一指标泛函下达到最优。

基于导弹编队过程中各成员位置和速度的累计误差,所建立的指标泛函为

(22)

结合式(10)和式(11)可得

(23)

由此,将指标泛函J转换为参数方程J(γ),在式(18)的约束下,待定系数γ的最优值可由下式得出[14]，即

(24)

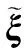
(25)

在上述假设条件下,式(10)所表示的闭环系统方程简化式为

(26)

式(26)为二阶微分方程形式,为了保证闭环系统的稳定性,消除非周期性规律变化的起始误差,待定系数γ应满足

(27)

式(26)的解为

(28)

式中

将式(28)代入式(25),可得参数化指标函数为

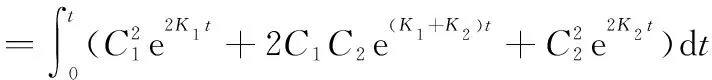
(29)

由于K1<0和K2<0,仅考虑稳态过程,则

(30)

进而待定系数γ的最优值可由式(24)得出。

结构优化和参数优化是解决最优控制问题的基本过程,在式(7)给出控制算法结构的基础上,通过上述方法即可实现对控制算法的参数优化,从而进一步提高了导弹编队系统的性能。

3 仿真实例

下面仿真验证控制算法式(7)的有效性。仿真条件如下:

条件1假设领弹装备有合成孔径雷达导引头(synthetic aperture radar seeker, SARS),受成像分辨率和脱靶量约束,其制导律算法[13]为

(31)

式中,jh和jv分别为领弹水平面控制量和垂直面控制量;V和R分别为弹目相对速度和相对距离;φ和ω分别为导弹前置角和目标线角速度;β为弹目高低角;q11/k1和q22/k1均为权值系数,其他与SARS相关的仿真参数详见文献[13]。领弹的初始位置坐标为(0, 5 km,0),初始速度为(500 m/s, 0, 200 m/s);目标位置坐标为(40 km, 5 km, 40 km)。

条件2从弹1的初始位置坐标为(2 km, 7 km, 0),初始速度为(800 m/s, 0, 300 m/s);从弹2的初始位置坐标为(0, 3 km, 2 km),初始速度为(700 m/s, 0, 200 m/s)。

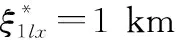
≤εξ

条件4设导弹自动驾驶仪惯性环节时间常数τ=0.3 s,经参数优化取γ=9。

在式(7)作用下,导弹编队运动轨迹如图3所示。

图3 三维空间导弹轨迹Fig.3 Missiles trajectory in 3D space

如图3可知,由于算法式中一致性项的作用,可实现编队队形的快速收敛,仿真t=48 s时收敛至预期的队形,仿真时间48～97 s,算法实现了对预期队形的保持。

图4给出了从弹1和从弹2与预期位置的相对误差随制导时间的变化规律。

图4 从弹相对位置误差Fig.4 Followers relative position error

在式(7)的作用下,随着制导时间的增加,从弹1及从弹2的相对位置误差趋于零。图5给出了从弹1与领弹相对速度的变化情况。

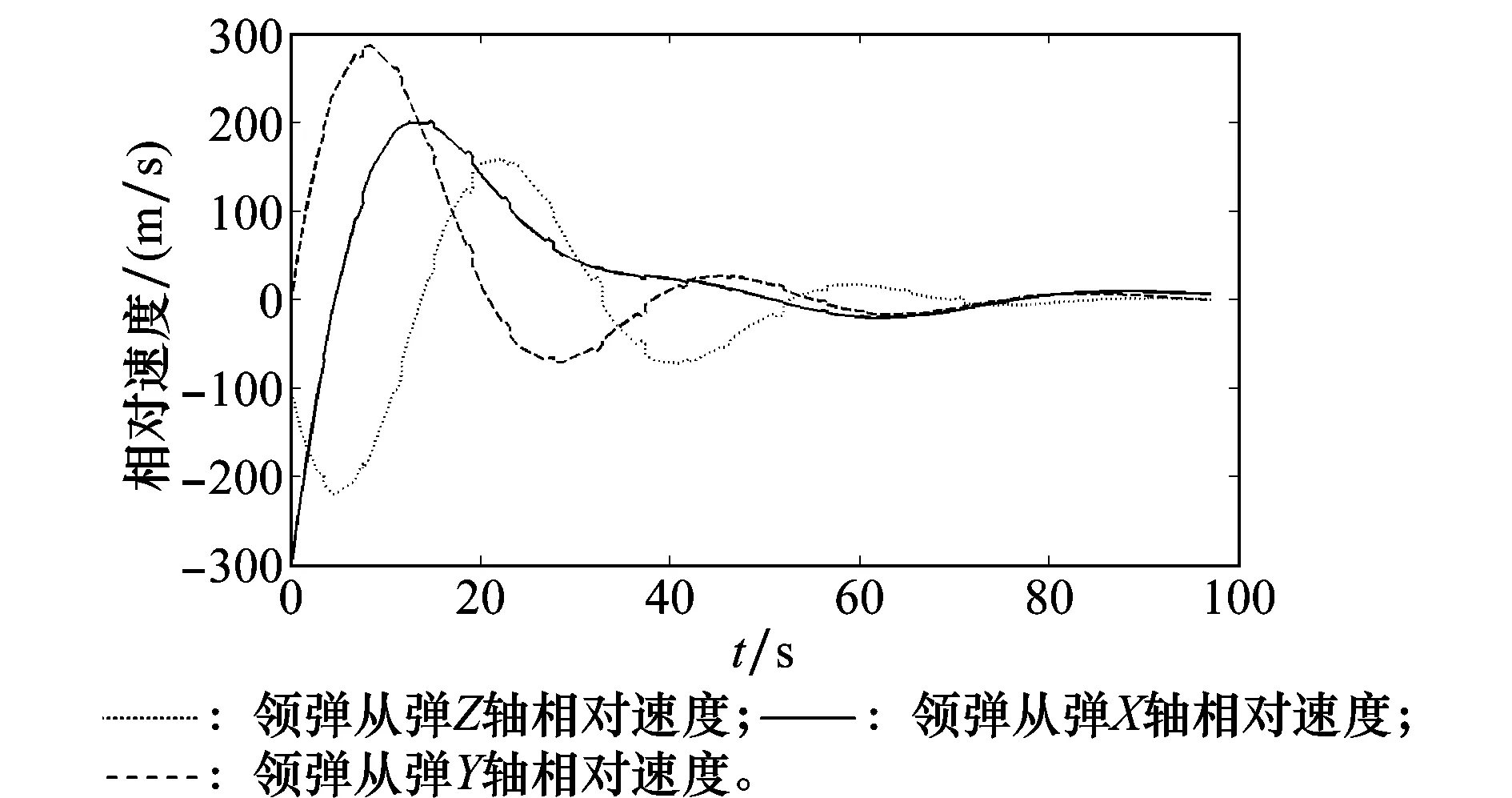
图5 从弹与领弹相对速度Fig.5 Relative velocity between leader and follower

由图5可知,在控制算法的作用下,导弹编队可实现位置和速度收敛。图6给出了地理坐标系下从弹1加速度矢量随制导时间的变化规律。

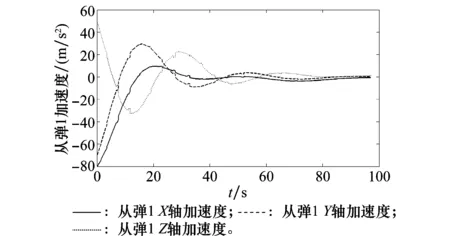
图6 从弹1加速度Fig.6 Follower1 acceleration

各轴向加速度分量在制导初始阶段较大,随着编队队形的逐步收敛而不断减小。

图7给出了编队控制过程中,在以从弹1质心为坐标原点建立的弹道坐标系下,从弹1所需的控制力矢量随制导时间的变化规律,与空气阻力X相关的参数为:空气密度ρ=1.2 kg/m3导弹的质量为m=200 kg;阻力系数c=0.1;导弹的特征面积为S=0.15 m2。

图7 从弹1需用控制力Fig.7 Follower1 required control force

由图7可知,从弹1各轴向控制力分量随制导时间的增加不断减小,结合某型导弹装备实际,令导弹极限过载nmax=38g,所需控制力分量均在限定范围之内。

图8给出了在未经参数优化情况下,从弹位置误差的变化规律,令γ=7,仿真t=88 s时生成了既定的编队队形,88～97 s为队形保持阶段。

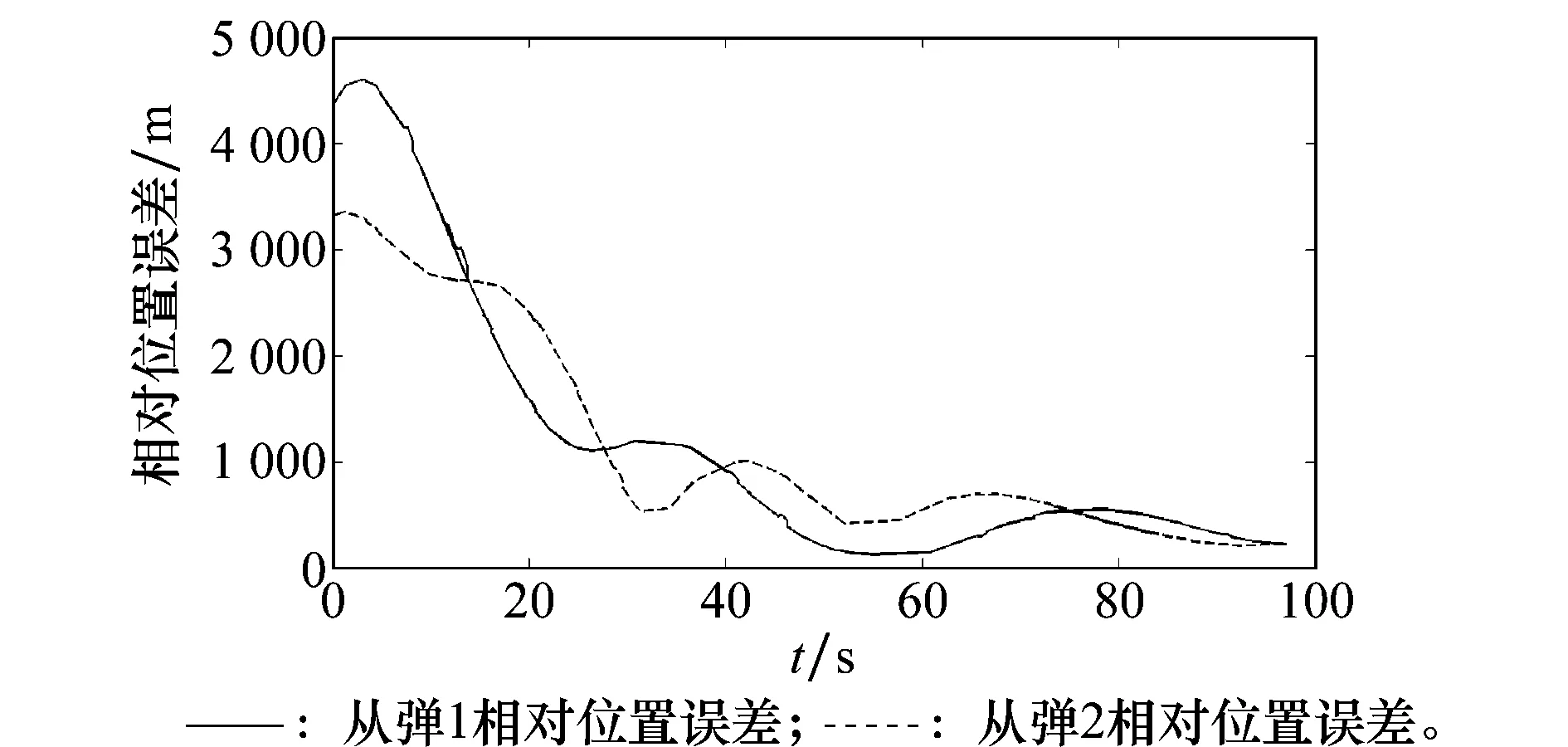
图8 未参数优化的位置误差Fig.8 Position errors without parameter optimization

对比参数优化情况(见图4),队形收敛时间增加,位置和速度累计误差增大。

为了进一步说明本文算法的创新性,下面对文献[9]所提出的编队控制算法进行仿真,算法[9]式为

ζi

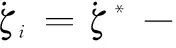
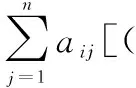
(32)

式中,ξi和ζi分别表示导弹编队成员i的位置和速度;ξ*和ζ*分别表示理想位置和理想速度;β和γ均为算法系数,设定β=1和γ=1。导弹编队由3枚导弹组成,编队拓扑网络中含有一棵以领弹为根节点的有向生成树,其领弹的运动状态不受从弹影响,领弹和从弹的初始位置和初始速度如前所述;设定理想位置ξ*=ξl以及理想速度ζ*=ζl,ξl和ζl分别表示领弹位置和领弹速度。各枚导弹在三维空间的运动轨迹如图9所示。

图9 应用算法式(32)的编队轨迹Fig.9 Formation trajectory based on equation (32)

由图9可知,在式(32)的作用下,3枚导弹的位置收敛且速度趋于一致。然而,由于式(32)中不能设定导弹各成员间的相对位置关系参数,相比本文提出的控制算法,不能实现既定位置关系的生成和保持,仅能使编队各成员的位置收敛至同一平衡点;再者,式(32)在设计过程中未涉及自动驾驶仪动态特性和参数优化过程,实际应用过程中,闭环制导控制系统不能保证渐进稳定性和优性。综合上述分析,本文提出的导弹编队控制算法相比文献[9],更加适用于导弹编队队形控制过程。

4 结 论

基于多智能体一致性理论,设计适用于领从结构导弹编队控制过程的制导律算法,研究总结如下:①将导弹自动驾驶仪简化为一阶惯性环节,基于坐标变换,得到了导弹控制力与制导指令之间的关系模型;②建立了基于一致性理论的导弹编队控制算法,实现编队成员趋于理想位置的同时,速度趋于一致,适用于编队队形的生成与保持;③提出了参数优化方法,实现待定系数的取值在某一指标泛函下达到最优。该算法对于导弹编队系统的总体设计具有一定的理论参考价值。