反舰导弹区域射击方法研究

贾正荣, 卢发兴, 王航宇

(海军工程大学电子工程学院, 湖北 武汉 430033)

0 引 言

复杂电磁环境下,目标定位精度下降,在这种条件下,有时必须使用反舰导弹(anti-ship missile, ASM)对大散布目标实施攻击[1],才能够先敌攻击、占据优势。其中,射击方案的优劣直接影响了这种情况下的ASM射击效能,因此,研究对大散布目标的射击方案求解方法具有重要的军事意义[2-3]。

对于大散布目标的ASM射击方案求解有一定的研究历史。文献[4]认为目标精度显著降低后,继续采用传统的前置点射击方法、现在点射击方法,导弹对目标的捕获概率将会很低,无法满足作战要求,因此提出了人工散布方法,使每发导弹的射击瞄准点在方向上人为地偏移目标散布中心某一位置或某一角度,从而形成一个较大的射击扇面,这样就可以提高对大散布目标的捕获概率,但是该文献只分析了不同ASM数量条件下,改变弹间射击瞄准点间隔对于捕获概率的影响,并没有给出具体的优化求解方法。文献[5]研究了各种因素对于ASM捕获概率的影响,认为ASM的发射距离与搜索范围是影响捕获概率的主要因素,同时当目标定位精度较低时,采用现在点方式将无法完全覆盖目标散布区域。随着ASM发射距离的增加,导弹的自控终点误差、目标机动散布误差都会对射击效能产生较大影响[6],文献[7]研究了复杂条件下各因素对于ASM命中精度的影响,认为对于大散布目标,应当采用扩散射击方法,才能达到先敌发射和先敌命中的目的,同时给出了具体的扩散射击方案求解方法,能够求解扩散射击时各瞄准点的间隔及所需ASM总数,但是其瞄准点的求解并未考虑对应的捕获概率,而是以几何方式直接给出。文献[8]研究了具有末制导搜索能力武器的区域射击方法,在理论上给出了多弹覆盖攻击时的最优毁伤概率,但是缺少对于方案所需ASM总数的求解方法。文献[9]提出了多弹区域覆盖平行搜索方法,给出了具体的等间隔平行搜索瞄准点间隔计算方法。另外,随着ASM航路规划能力的提升,文献[10]增加了对多弹攻击时航路规划能力的考虑,提出了盲目射击攻击模型,并对具体的射击方案性能进行了分析。

事实上,对于大散布目标,首先综合考虑各类误差得到目标散布区域大小,进而根据目标散布区域大小决定所需ASM总数、配置多枚ASM的射击瞄准点,最后得到完整的射击方案,已经成为求解该问题的基本框架。然而,现有研究仍存在一定的不足:①在求解所需ASM总数时,仅考虑多弹的搜索区域能够覆盖多大的空间,而没有定量地考虑能够达到多高的捕获概率;②在求解瞄准点配置间隔时,存在进一步优化的空间;③方法缺少体系性,大多数研究只着眼于射击方案求解的部分问题,且不同研究的兼容性不强,难以综合给出完整的射击方案求解方法。

本文提出ASM的区域射击方法,从兼顾捕获概率与毁伤概率的角度出发,通过变分手段求取捕获概率与毁伤概率的理论最优值[11-12],同时结合ASM的战术应用特点,将ASM区域射击方案求解划分为3个子问题:即满足预定捕获概率的可用瞄准点间隔范围计算方法、对应最优毁伤概率的瞄准点间隔计算方法、ASM数量计算方法。针对3个子问题分别建立模型,最后给出完整的射击方案求解流程。

1 问题分析

1.1 问题建模

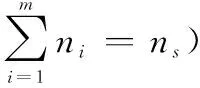
目标函数为

(1)

约束条件为

(2)

计算捕获概率与毁伤概率时,还需要ASM自控终点散布误差Ex1、目标散布误差Ex2、反舰导弹瞄准点位置xi、导弹搜索半宽B、捕获后毁伤目标的概率Q等参数。为简化分析,以不相关误差Ex1为基准,对部分参数进行归一化处理,得到归一化的射击误差ε=Ex2/Ex1、归一化瞄准点位置ξi=xi/Ex1、归一化瞄准点间隔Δξ=Δx/Ex1与归一化搜索半宽b=B/Ex1。从而给出多枚ASM对目标的捕获概率为

ξi)]nidx

(3)

多枚反舰导弹对目标的毁伤概率为

ξi)]nidx

(4)

式中,f(x)是目标散布概率密度函数,典型的分布有正态分布与均匀分布;p(ξ)是捕获判断函数,即

(5)

式中,ρ为标准差与概率误差的转换系数,取0.476 936。

在等间隔配置原则下,瞄准点位置ξi可以通过瞄准点间隔计算得到,有

Δξ+(i-1)Δξ

(6)

1.2 方案求解流程

经过分析,为了使区域射击方案能够满足预定捕获概率的要求,首先应当通过预定捕获概率计算出一个瞄准点间隔的范围,在这一范围内,瞄准点间隔的取值均能使捕获概率满足要求,之后在这一范围内求毁伤概率的最优值及对应的瞄准点间隔。同时考虑到应当减少ASM总数,则应当从一个较小的ASM总数初值开始,不断校正ASM总数,直到捕获概率与毁伤概率满足要求。综上,具体的求解步骤为:

步骤1设定一个ASM总数初值ns;

步骤2给出当前ASM总数条件下的瞄准点数量、每个瞄准点分配反舰导弹数量的组合(m,ni);

步骤3针对每一个(m,ni),求解满足预定捕获概率PC,S的所有瞄准点间隔Δξ,作为可用瞄准点间隔范围DΔξ,在Δξ∈DΔξ内,求解毁伤概率的最大值;

步骤4若存在(m,ni)组合下的一个瞄准点间隔Δξ,使捕获概率与毁伤概率同时满足预定要求,则求解完成,将此时的m、ni与Δξ作为结果;

步骤5若所有(m,ni)组合对应的捕获概率或毁伤概率均无法满足预定要求,则根据一定原则校正反舰导弹总数ns,从步骤2重新开始。

对应的射击方案求解流程如图1所示。综上,为实现对区域射击问题的求解,需要解决以下几个问题:①满足预定捕获概率的可用瞄准点间隔范围的计算；②对应该范围内毁伤概率最大值的最优瞄准点间隔的计算；③ASM数量的计算(包括ASM总数初值的计算与校正、瞄准点数量与每个瞄准点分配的ASM数量计算)。

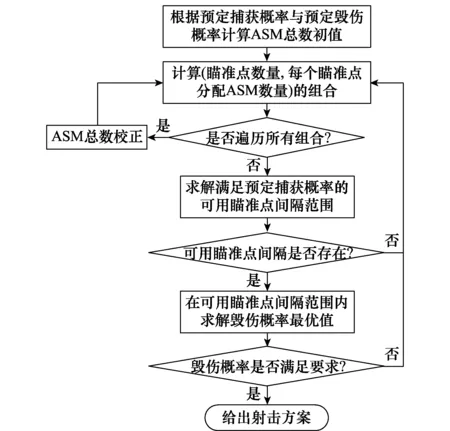
图1 ASM区域射击方案求解流程Fig.1 Solution process of regional shooting scheme for ASM

2 可用瞄准点间隔范围计算方法

在给定瞄准点数量m与每个瞄准点分配反舰导弹数量ni条件下,求解可用瞄准点间隔范围。首先,应当判断该范围是否存在,之后再求解具体范围的大小。

2.1 存在性判断

可以通过捕获概率PC关于Δξ的最大值maxPC是否满足预定要求PC,S进行判断,即当

maxPC(Δξ)≥PC,S

(7)

时,才存在DΔξ,使

∀Δξ∈DΔξ,PC(Δξ)≥PC,S

(8)

根据PC(Δξ)的性质,∃ξC,当Δξ>∃ξC时,有

(9)

从而可以通过二分法求解maxPC及对应的瞄准点间隔(记为ΔξC,max):设二分法两个端点的初值为0与ξC(可以取C倍搜索半宽b),按照一般的二分法即可求解得到ΔξC,max以及对应的PC(ΔξC,max)。之后根据式(7)即可判断是否存在可用瞄准点间隔范围。

2.2 可用瞄准点间隔范围求解

由于PC(Δξ)的连续性,可用瞄准点间隔范围DΔξ必然包含ΔξC,max的一个邻域。事实上,精确的DΔξ可能由多个不连通的区间DΔξ,i组成,即

DΔξ=∪DΔξ,i

(10)

计算Δξ上所有的DΔξ,i较为复杂,在实际使用中,为了提高计算效率,只计算包含ΔξC,max的区间,并将此区间作为可用瞄准点间隔范围DΔξ。

设DΔξ=[Δξa,Δξb],显然,有

(11)

求解两端点Δξa与Δξb的方法较多,二分法、牛顿迭代法均可求解[13-16]。

3 最优瞄准点间隔计算方法

对于典型的目标分布,现有文献已经给出较为详尽的求解最优瞄准点间隔的方法。对于服从正态分布的目标,可以采用文献[8]中变分方法求解。

设射击密度函数为

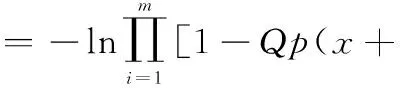
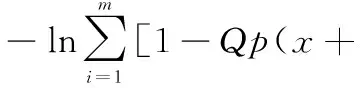
(12)

则U(x,Δξ)是瞄准点间隔Δξ的函数,存在最优的射击密度函数为

(13)

式中,RK为

(14)

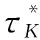
(15)

在Δξ∈DΔξ上优化Δξ的取值,使U(x,Δξ)-UO(x)最小,即可求得可用瞄准点间隔范围内的最优毁伤概率以及对应的最优瞄准点间隔。

4 ASM数量计算方法

4.1 ASM总数初值计算

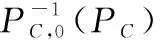
(16)

代入预定毁伤概率PC,S,得到反舰导弹总数初值ns,0为

(17)

当目标散布服从正态分布时,有PC,O(ns)为

(18)

式中,RC为

(19)

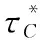
(20)

同理,可得最优毁伤概率为

(21)

由于PC,O(ns)与PK,O(ns)不是ns的显函数,这里构建不动点迭代函数求解ns,因而有

(22)

而有

(23)

PC,O(ns)与PK,O(ns)是关于ns的捕获概率最优值,因此无论瞄准点数量、每个瞄准点分配反舰导弹数量以及瞄准点间隔取何值,均有实际捕获概率PC(ns)与实际毁伤概率PK(ns)小于等于捕获概率最优值PC,O(ns)与PK,O(ns),即

(24)

取ASM总数初值ns,0为

ns,0=max{ns,C,ns,K}

因而有ASM总数初值ns,0小于等于实际所需ASM总数ns,即

ns,0≤ns

(25)

因此,需要在ns,0的基础上对ASM总数进行修正。

4.2 瞄准点数量-每个瞄准点分配ASM数量计算方法

给定ASM总数ns后,需要给出所有的瞄准点数量、每个瞄准点分配ASM数量的组合(m,ni)。显然,这些组合应当满足两个基本条件:

条件1瞄准点数量m不大于导弹总数ns;

条件2每个瞄准点上至少分配一枚导弹。

因此,给出所有组合的方法是,对于每个瞄准点数量的取值,给出满足条件2的所有ni的排列。算法具体步骤为:

步骤1从1开始,到ns结束,作为m的取值;

步骤2对于给定的m,求满足式(26)的所有组合;

(26)

步骤3对于所有组合,分别求所有元素的排列。

在求解过程中,可能出现相同m情况下,组合相同或排列相同的情况,这时需要将重复的排列或组合删去;另外,由于瞄准点配置一般关于坐标原点对称,对于最终求得的排列,应当将对称的排列删去。

值得注意的是,由于需要求解向量排列,当向量内元素较多时,时间复杂度将无法接收。因此当ASM总数大于一定值时,可以采用将ASM平均分配至每个瞄准点的方法进行求解。

4.3 ASM总数修正方法

采用线性外推法对ASM总数进行迭代修正[17-18],当可用瞄准点区间不存在(即捕获概率不满足预定要求)时,有

(27)

当毁伤概率不满足预定要求时,则有

(28)

式中,|·|为向上取整。注意到,dPC(ns)/dns与dPK(ns)/dns分别为实际捕获概率与实际毁伤概率对ASM总数的导数,不仅计算复杂,而且与具体的瞄准点数量、瞄准点位置等参数相关。而在优化求解过程中,实际捕获概率PC(ns)与实际毁伤概率PK(ns)一般分别趋近于最优值PC,O(ns)与PK,O(ns),而形式PC,O(ns)与PK,O(ns)简单,仅与ns有关,因此用dPC,O(ns)/dns与dPK,O(ns)/dns代替式(27)与式(28)中的dPC(ns)/dns与dPK(ns)/dns,有

(29)

(30)

5 算例分析

首先验证本文方法的正确性,对于不同的误差条件,通过本文方法计算射击方案,根据射击方案通过统计模拟法求解实际捕获概率与毁伤概率并与理论计算结果进行对比。之后,在不同的误差条件下,通过本文方法计算射击方案,给出ASM数量计算结果,验证ASM数量计算方法的正确性。最后与现有方法进行对比,对于不同的误差条件,分别采用现有方法与本文方法求解射击方案,比较捕获概率与毁伤概率。

5.1 统计模拟法验证方法正确性

设舰艇采用同类ASM实施对海导攻,取预定捕获概率PC,S为0.95,预定毁伤概率PK,S为0.80。改变ASM捕获目标条件下毁伤目标的概率Q(分别取0.7、0.9)以及目标散布误差Ex2(取15～35 km),采用本文方法计算射击方案,根据射击方案采用统计模拟法计算实际捕获概率与毁伤概率[19],并与理论计算捕获概率与毁伤概率对比,如图2和图3所示。其中,图2为Q取0.7的情况,图3为Q取0.9的情况,统计模拟法得到的捕获概率与毁伤概率置信度为0.95;理论捕获概率为红色圈实线,对于每个Ex2取值的实际捕获概率,“×”为实际捕获概率均值,上下两个“+”所确定范围表示置信度0.95的区间。

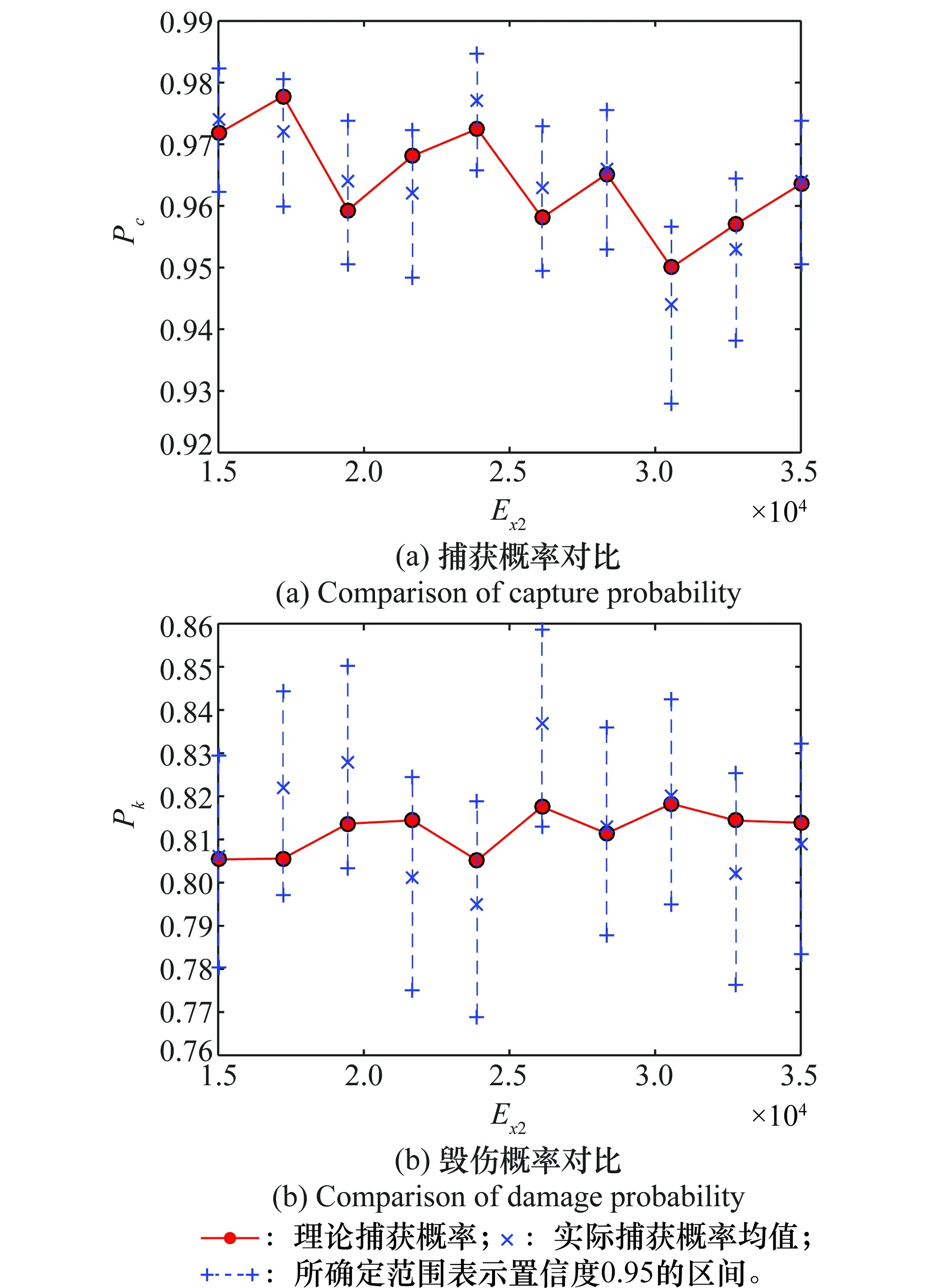
图2 理论结果与统计模拟法结果(Q=0.7)Fig.2 Results of theory and the results of statistical simulation (Q=0.7)

图3 理论结果与统计模拟法结果(Q=0.9)Fig.3 Results of theory and the results of statistical simulation (Q=0.9)

根据图2和图3的结果,本文方法可以计算出满足预定捕获概率与预定毁伤概率的射击方案,并且准确性较高,与统计模拟法结果对比,理论计算结果均能处于0.95置信度范围内。

5.2 ASM数量计算

为验证ASM数量计算方法的正确性,在不同误差条件下求解ASM区域射击方案,给出ASM数量计算结果,如图4所示。并将方案对应捕获概率、毁伤概率与最优捕获概率、最优毁伤概率进行对比。以验证ASM数量计算方法的正确性。

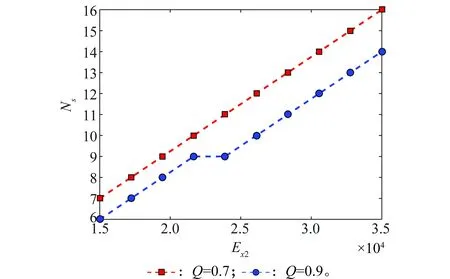
图4 ASM数量计算结果Fig.4 Numerical results of ASM

依然采用第5.1节中的仿真条件,在Q取0.7时计算得到ASM数量,捕获概率、毁伤概率与最优捕获概率、最优毁伤概率对比如图5所示。

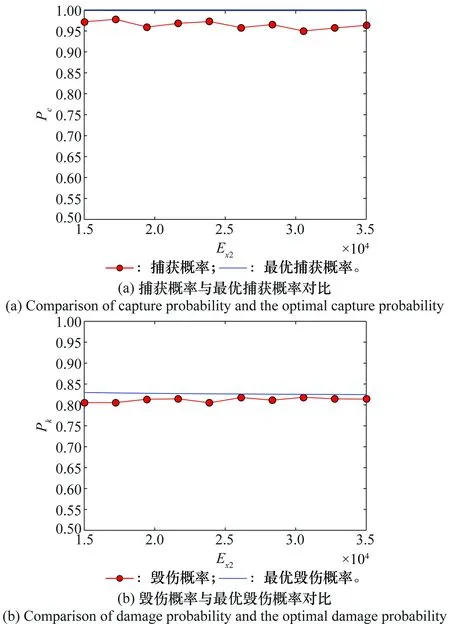
图5 捕获概率与毁伤概率同最优值对比(Q=0.7)Fig.5 Comparison of the same optimal value between the captureprobability and the damage probability (Q=0.7)

在Q取0.9时计算得到ASM数量,捕获概率、毁伤概率与最优捕获概率、最优毁伤概率对比如图6所示。

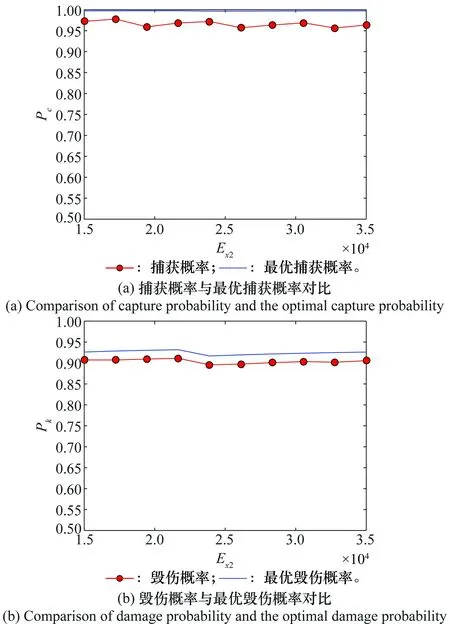
图6 捕获概率与毁伤概率同最优值对比(Q=0.9)Fig.6 Comparison of the same optimal value between the captureprobability and the damage probability (Q=0.9)

由图4～图6可得:在相同误差条件下,随着Q的下降,单枚ASM毁伤能力降低,导致方案需要更多ASM达到预定捕获概率与毁伤概率。同时,随着目标散布范围的增大,所需ASM数量也会增加。

另外,由图5和图6,方案对应捕获概率与毁伤概率不仅满足预定要求(预定捕获概率0.95,预定毁伤概率0.80),而且均趋近于通过式(18)与式(21)计算得到的理论最优值。

5.3 与现有方法对比

文献[9-10]探讨了ASM对大散布目标的射击方法(记为现有方法),具有较好的比较价值。根据文献[9-10],对于大散布目标,应当将多枚ASM按照等间隔平均分配至整个目标散布区,若目标散布服从正态分布,则有瞄准点间隔为

(31)

由于现有方法不能根据预定捕获概率或毁伤概率计算所需ASM总数,这里首先通过本文方法根据预定捕获概率与毁伤概率计算出ASM总数,之后以此数量通过现有方法计算射击方案。

取预定捕获概率PC,S为0.95,预定毁伤概率PK,S为0.80。ASM的自控终点散布误差Ex1为200 m,搜索半宽为10 km,改变ASM捕获目标条件下毁伤目标的概率Q(分别取0.5、0.9)以及目标散布误差Ex2(取15～35 km),分别采用现有方法与本文方法计算射击方案,并比较捕获概率、毁伤概率,如图7和图8所示(分别对应Q取0.5、0.9)。

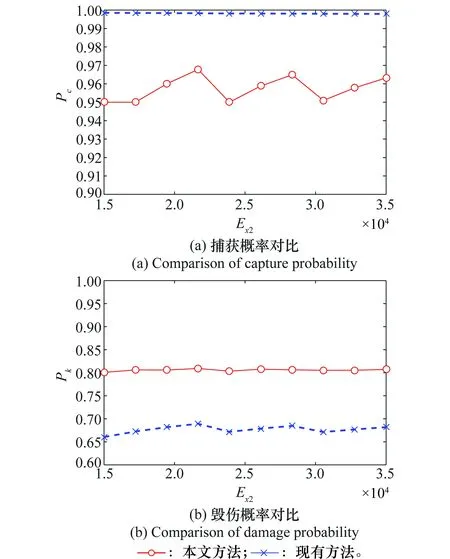
图7 现有方法与本文方法对比(Q=0.5)Fig.7 Comparison of existing methods and methods inthis paper (Q=0.5)

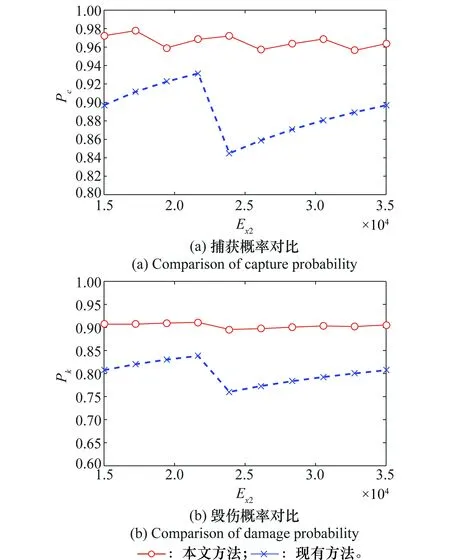
图8 现有方法与本文方法对比(Q=0.9)Fig.8 Comparison of existing methods and methods inthis paper (Q=0.9)

根据图7和图8:

(1)在Q取值较低(0.5)时,单枚ASM突防能力较低,现有方法的捕获概率高于本文方法,但是毁伤概率却无法达到预定要求,另外,此时现有方法的捕获概率与毁伤概率差值较大(达到0.35)。这是因为现有方法并未考虑射击方案的毁伤概率,当Q值较低时仍然以优化捕获概率为主,因而将瞄准点间隔配置得较大,使弹群分散,虽然确保了对目标散布区域的覆盖,但是可能无法有效毁伤目标。

这一差别可以通过图9和图10与表1说明。

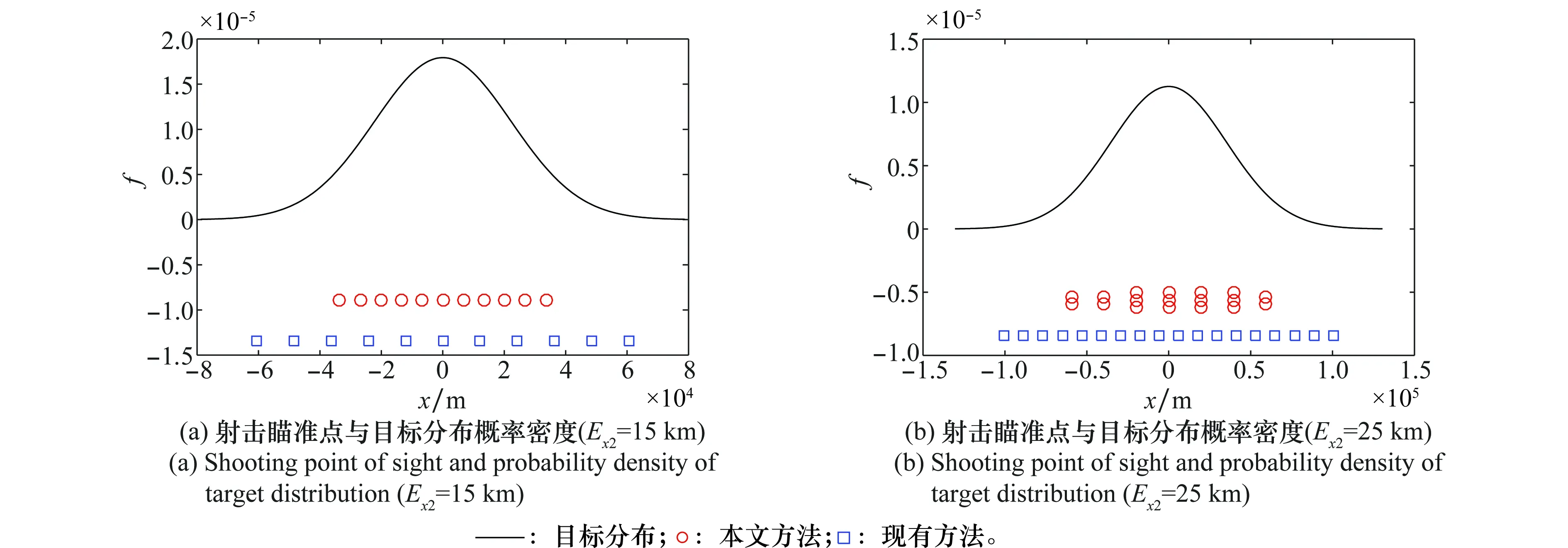
图9 射击瞄准点与目标分布概率密度(Q=0.5)Fig.9 Shooting point of sight and probability density of target distribution (Q=0.5)

图10 射击瞄准点与目标分布概率密度(Q=0.9)Fig.10 Shooting point of sight and probability density of target distribution (Q=0.9)

首先,引入覆盖比pse(即本文方法与现有方法瞄准点范围的比值):设本文方法求解得到的瞄准点为xs,i,现有方法为xe,i,则覆盖比为

(32)

图9和图10给出了Q值不同时,Ex2分别取15 km与25 km时的目标分布概率密度(黑色实线)、现有方法瞄准点配置(蓝色方框)与本文方法瞄准点配置(红色圆圈)。在图9中,由于Q值较小,单枚ASM毁伤目标的概率较低,本文方法将瞄准点紧缩配置,或在个别瞄准点配置多个ASM,使射弹密度增加,从而提高弹群对目标毁伤概率;在图10中,Q值较大,单枚ASM毁伤目标的概率较高,本文方法与现有方法求解得到的瞄准点覆盖比相比图9的更大。图9与图10对应的覆盖比如表1所示。

表1 瞄准点覆盖比

(2)在Q取值较高(0.9)时,本文方法在捕获概率与毁伤概率均优于现有方法。这是因为本文方法的优化程度更高,在相同ASM数量的条件下能够达到更优的捕获概率与毁伤概率。

(3)在瞄准点间隔的计算方面,现有方法倾向于完全覆盖目标散布区域以达到较高的捕获概率,而本文方法计算得到的瞄准点间隔受目标散布范围大小的影响较弱,因此结果较为稳定。本文方法在计算瞄准点间隔时,综合考虑了预定捕获概率、预定毁伤概率,是在满足预定捕获概率的可用瞄准点间隔范围内求取毁伤概率的最优值对应的瞄准点间隔。

(4)另外,本文方法增加了基于预定捕获概率与预定毁伤概率的ASM数量计算方法,能够给出实施对海导攻的主要决策参数。

综上,相比于现有方法,本文方法的主要改进有3点:①考虑了预定捕获概率与预定毁伤概率,给出了满足预定要求的射击方案,便于指挥决策;②给出了ASM数量的计算方法;③兼顾捕获概率与毁伤概率,结果较为稳定,且优化程度更高。

6 结束语

为进一步发挥ASM的搜捕优势,需要充分考虑并优化射击方案的捕获概率与毁伤概率,进而给出完整的射击方案求解方法。本文结合ASM应用特点,提出了ASM的区域射击方法,方法能够满足预定捕获概率与毁伤概率的要求,体系性较强,准确性较高。相比于现有方法,在优化程度上有一定提升,并且给出了更为完备的射击指挥参数与射击方案求解流程,能够为ASM的战术应用提供更好的理论与技术支撑。