基于GA-SA的低轨星座传感器资源调度算法

刘建业, 王 华, 周晚萌

(国防科技大学空天科学学院, 湖南 长沙 410073)

0 引 言

天基预警卫星系统是完整弹道导弹防御体系中的一个重要环节,它可以近实时地发现并监视弹道导弹等目标。其中,天基红外低轨星座(如STSS)能够对自由段弹道进行全程跟踪监视,可以无缝接力高轨星座对目标的观测,因此受到越来越多的重视,成为导弹防御体系中的重要一环。低轨星座一般采取24星部署,分布于3个轨道面,轨道高度约1 600 km。因此,在对目标进行跟踪监视时,系统不可避免的需要进行多传感器对多目标调度问题的求解,这是一个典型的组合优化NP-hard问题。目前,受保密条例限制,很难获取国外有关预警卫星传感器方面的资源,只能查阅借鉴一些一般领域的调度方法,Fatos等[1]利用遗传算法对对地观测卫星的传感器资源调度管理进行了研究,相较随机搜索其计算效率有了很大提升;Ayed等[2]针对卫星广播调度问题,以卫星成功调度次数为目标函数,采用二进制编码的差分进化算法对该调度问题进行求解;文献[3-4]提出了一种基于任务合并的蚁群优化算法,可以将调度问题规模减少从而提高求解效;文献[5]采用分布式凸优化方法,提出了一种针对N维离散线性时间系统的随机调度策略;Hernadez M L[6]针对单目标跟踪问题,提出了一种基于后验克拉美-罗下界(posterior Cramer-Rao lower bound,PCRLB)的传感器管理方法,是一种以跟踪精度为优化目标的传感器管理方法;Shudai等[7]针对柔性车间调度问题,提出了一种高效的启发式遗传算法,可以有效的降低加工成本;文献[8]针对多目标贝叶斯滤波,以后验期望误差为优化目标,基于部分可观察马尔可夫决策过程,提出了一种传感器控制方法;文献[9]以目标跟踪过程中的预测协方差矩阵为控制变量,同时考虑传感器使用时的能量消耗,设计了一种可以延长传感器使用生命周期的调度方法。

国内针对预警系统传感器资源调度问题的研究也还处于发展阶段。李国辉等[10]以调度成功率、目标跟踪精度以及传感器网络的能源消耗为指标,提出了一种分群粒子群优化的传感器调度方法,但该方法是一种全局最优解,需要全部的弹道信息,而实际的预警过程中无法提前获取全部信息,且全局优化比较耗时;赵砚等[11]利用PCRLB计算不同传感器调度方案带来的信息增量差别,设计了基于PCRLB的传感器滚动时域调度算法,然而仅考虑跟踪精度的调度策略,可能会使卫星工作超载导致系统产生故障;文献[12]提出了卫星贡献度的概念,并以卫星贡献度、观测切换率以及卫星松弛度为目标函数,采用遗传算法求解卫星调度策略,但是其需假设目标弹道为提前已知;文献[13]通过分析预警实际需求,设计了一种预警卫星传感器资源调度策略,但是该方法只能针对一些特殊的场景,应用范围有限;文献[14-15]采用改进的粒子群算法对预警任务进行规划调度,但是其均缺少对目标的跟踪能力研究,与实际需求有所偏颇;文献[16]基于预警卫星传感器探测原理,设计了一种基于聚类的预警卫星传感器资源调度方法,但是其调度策略仅考虑了跟踪精度,缺少对系统工作效率的考量;目前,针对调度问题研究比较成熟的是车间调度问题,文献[17-18]采用了遗传算法对车间调度问题进行求解,该求解方法对于卫星传感器资源调度具有一定的参考性。

上述研究为预警卫星传感器资源的调度建立了基础,有效提高了预警系统的工作性能,但是在预警任务规划的实时性与系统利用的全面性方面还有改进之处:①文献[11,16]缺乏对系统工作效率的考虑,其调度策略可能会使系统负载过大以致产生故障,文献[14-15]的关注点为任务的成功执行,缺乏对跟踪精度的考虑,这与实际需求有所不符;②文献[10,12]需要假设目标弹道为已知,然后进行全弹道预警任务规划,与预警真实约束是不符的。

因此,本文综合考虑了调度的实时性与性能评价的全面性,采用滚动周期调度的方法,以调度周期内的PCRLB变化率表征系统信息增量,以卫星跟踪目标的切换率衡量系统工作效率,建立了以跟踪精度与卫星切换率为目标的传感器调度混合整数规划模型,然后采用GA-SA混合优化算法求解传感器调度策略。最后,仿真实验表明本文算法可以在保证跟踪精度的同时,很好的兼顾到系统效率,对未来的预警卫星反导具有一定的参考价值。

1 目标跟踪模型

对于目标跟踪,假设在某一时刻选择卫星传感器对该目标进行探测,则对目标进行跟踪的过程就是利用各传感器在某时刻探测到的目标信息,基于一定的跟踪模型并采用相应的滤波器进行该时刻目标状态估计的过程。

(1)

对于目标观测,本文采用双卫星对运动目标进行探测,通过卫星上的红外敏感器测量机动目标相对卫星的方位角与仰角。目标相对各卫星的视线矢量方向在卫星轨道坐标系中用方位角A与仰角E表示,如图1所示。

图1 观测模型Fig.1 Observation model

(2)

由图1可知,目标方位角、仰角计算为

(3)

从而目标双星观测模型为

νk+1,i=1,2

(4)

基于上述目标跟踪模型,在结合相应的滤波器,就可以实现对目标的跟踪估计。

2 调度评价指标

建立合理的评价指标是进行调度的前提和依据。考虑到跟踪精度与系统工作效率,从两个方面建立评价指标。首先从跟踪精度的角度出发,需要保证每个调度周期内传感器系统获取足够的目标跟踪信息,这一指标以调度周期内目标跟踪的PCRLB变化率来定量描述;其次,从传感器系统工作效率的角度出发,需要尽可能减少传感器的损耗并提高跟踪的稳定性,这一指标以传感器切换率来定量描述。因此,调度评价指标就由表示系统信息量获取的PCRLB变化率,表示系统效率的传感器切换率构成。目标函数由它们加权求和计算,各指标的权值通过经验确定。

PCRLB是系统可达最佳跟踪性能的一种度量,作为任何无偏估计方差的下界,它给出了一定假设条件下状态估计的方差极限,在状态估计的统计性能分析中扮演着重要角色。所以本文以每个调度周期内PCRLB的变化率来衡量系统跟踪性能。

PCRLB代表了某时刻对目标估计值与真值的误差协方差阵的下界,即

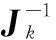
(5)

(6)

式中,Qk-1为系统过程噪声噪声方差;Rk为观测噪声方差,Φk-1为状态转移矩阵;Hk为观测矩阵。每个状态变量的PCRLB定义为信息矩阵逆的相应对角线元素的平方根,即

(7)

同时,考虑到卫星红外探测器的观测量只与目标状态的位置分量有关,进行目标状态滤波的测量更新时,观测量只对位置分量的估计有贡献,因此最终定义调度周期内PCRLB变化率,即系统信息增量为

(8)

式中,M表示调度周期内追踪目标数量,分母项表示调度周期开始时刻所有追踪目标的位置分量的PCRLB之和,分子项表示调度周期内所有追踪目标位置分量的PCRLB变化量之和。

在整个调度周期内,在考虑跟踪精度的同时,也需要兼顾系统效率,由此引入可以用于描述参与调度的所有卫星传感器资源运行效率的指标,本文通过统计卫星观测目标变换次数,进而确定卫星切换率来描述预警系统的工作效率。

考虑到PCRLB变化率指标为越大调度效果越好,因此卫星传感器切换率计算按式(9)计算,SS越大,表明卫星切换率越低,卫星监视效率越高。

(9)

式中,M表示跟踪的目标数量;switchi表示第i个参与跟踪的卫星在整个调度周期内更换跟踪目标的次数;Ni表示目标i的观测任务数量。

3 调度优化算法

3.1 调度模型

以调度周期内系统跟踪目标的PCRLB变化率与卫星切换率加权求和得到目标函数,进一步考虑卫星与目标运动状态的可预测性,建立预警系统周期调度优化模型,具体为

maxf=ω1ΔI+ω2SS

s.t.ω1+ω2=1

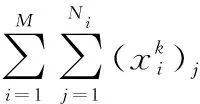
(10)

3.2 基于GA-SA的混合优化算法

GA算法[18]是一种基于“适者生存”的进化算法,它把问题参数编码为染色体,再利用迭代方式进行选择、交叉及变异等运算来交换种群中染色体的信息,最终生成符合优化目标的染色体。该算法具有编码与遗传操作简单,隐含并行和全局搜索的优点,但是其进化缓慢、易早熟、局部寻优能力差等缺点。SA算法[18]的出发点是基于物理物理固体物质的退火过程与一般组合优化问题之间的相似性,利用Metropolis准则以一定概率接受恶化解从而跳离局部最优的陷阱,但是其全部收敛的时间性能较差。GA-SA算法结合了二者的特点,使两种算法优势互补,提高了问题求解的效率。

基于GA-SA算法的特点,本文采用该算法求解预警系统传感器资源调度策略,算法流程如下:

步骤1建立卫星传感器资源集S与目标集T。

步骤2建立调度周期内各目标观测子任务集OPi,j。

步骤3目标与卫星轨迹预测,根据各种约束条件建立各目标观测子任务集OPi,j对应的传感器资源集OPSi,j,其中传感器资源的建立采用均匀划分可见时间弧段的方法进行,具体方法如图2所示。

图2 目标观测子任务划分示意图Fig.2 Submission partitioning of target observation

其中,针对在子任务时间弧段内卫星观测时间不足的传感器资源,如[0,10]窗口内的卫星S2,如果其可见时长不足任务时间弧段的一半,则将其舍弃,否则将其作为该子任务的伪传感器资源,使用时在该资源不可见时段内采用单星滤波的方法对目标进行跟踪。

步骤4执行GA-SA优化算法,计算调度决策,如图3所示,然后当预警时间推进到当前调度周期时,执行该调度决策,进行目标的跟踪估计。

图3 GA-SA算法流程Fig.3 Flow chart of GA-SA

步骤5预警未结束则重复执行步骤3到步骤4,否则预警结束。

除此之外,采用GA-SA算法,其优化算子需要特别的设计,具体方法为:

(1) 调度染色体编码策略

染色体采用基于观测任务与预警传感器资源一一对应的多层整数编码技术,每条染色体表示调度周期内所有卫星传感器对目标的观测序列。设每个目标在调度周期内的观测序列为P个,则染色体个体长度为3MP。其中,染色体前1/3表示所有目标的观测序列,后2/3表示每次观测对应的卫星编号,且当目标的某次观测只有一颗卫星或没有可用卫星时,在染色体卫星编号处将该次观测的卫星编号以0取两次表示,编码实例如图4所示。

图4 编码示意图
Fig.4 Sketch map of encoding

(2) 适应度函数:最优调度就是使得目标函数f取得最大值的调度,因此将目标函数f作为染色体个体的适应度函数。

(3) 交叉、变异操作:以交叉概率Pc随机从父代中选择两个个体进行交叉运算。从编码设计可以看出,染色体目标序列代表了观测时间顺序,因此交叉点发生在目标序列位置处,同时其对应的观测卫星也一同交叉。本文基于此原理采用顺序交叉方法,可以保留并融合不同排列的染色体结构;变异操作采用单点位置变异方式,首先从父代种群中随机选择变异个体,并以变异概率Pm选择变异的目标序列位置,然后利用该序列处观测目标的当前可用卫星进行随机置换。

(4) Metropolis准则抽样:计算交叉变异前后的个体适应度变化量,即

Δf=f(father)-f(son)

(11)

如果Δf<0,则接受新的个体为当前个体;否则计算p=exp(-Δf/T),其中T为当前温度,如果p>rand,也接受新的个体为当前个体;否则保留父代个体为当前个体。

(5) 算法终止:结束条件设置为当连续10代种群的平均适应度值小于某一极小阈值时,算法终止,否则按照Tk=αTk-1进行退温,并叠加进化代数,继续执行算法。

4 仿真结果及分析

本文仿真场景中,天基预警系统星座采用3×8部署,包含3条轨道,每条轨道上均匀布置8颗卫星,卫星间隔45°,卫星高度1 600 km,轨道倾角103°,卫星传感器采样频率设置为1 s,观测误差σLOS=100 μrad,调度周期70 s,目标跟踪估计采用UKF算法。利用STK软件生成3个待跟踪目标,在发射后40 s进入自由段。目标具体参数如表1所示。

表1 目标参数表

针对上述场景设置,本文利用8.00 GB RAM的Intel(R)/3.40 GHz进行仿真,以Matlab R2016b为仿真软件。算法参数设置为:交叉概率Pc=0.6,变异概率Pm=0.5,种群规模N=100,最大进化代数Gen=50,初温T0=80°,退温速率α=0.8,目标函数权值的取法为:当ΔI>0.75时,ω1=0.7、ω2=0.3;当ΔI≤0.75时,ω1=0.2、ω2=0.8。这是因为随着目标跟踪估计的稳定,目标估计的PCRLB变化率,即ΔI会逐渐减少,甚至当跟踪收敛时,ΔI会趋于零,此时需将ΔI的权值减少。

仿真计算时将目标的预警观测任务等时间间隔(10 s)划分为21个子任务,并分别采用GA与GA-SA混合算法进行迭代求解,第一个调度周期内的迭代过程如图5所示。

图5 GA-SA与GA算法迭代过程Fig.5 Iteration of GA and GA-SA

由图4可以看出,GA-SA混合算法相较GA算法,其对最优解的搜索具有更高的效率,在相同的迭代次数内扩大解的搜索范围,从而可以得到更优的解。

第1个调度周期内各调度方案下优化指标见表2。

表2 GA与GA-SA优化结果

可知对于本文场景下的预警系统低轨星座传感器资源调度,GA-SA的优化结果总体上较GA优一些,对于表中的切换率,由式(9)可知,GA-SA与GA的实际切换率分别为0.112 9和0.095 2,可见GA-SA算法切换率指标也更优。之后的调度周期内,随着预警系统对目标跟踪估计的逐渐收敛,指标ΔI会逐渐减少至趋于零,此时通过判断ΔI大小更换目标函数权值,算法更注重系统切换率水平,从而提高跟踪效率。

预警全过程内目标的跟踪误差如图6所示。

图6 GA-SA与GA算法跟踪误差图Fig.6 Target tracking errors of GA-SA and GA

从图6中可以看出,相较GA算法,GA-SA混合算法在跟踪精度方面具有更大的优势,同时,GA-SA算法优化的调度策略跟踪收敛速度也更快一些,这是因为GA-SA优化结果下的调度策略,其卫星切换率低,对目标的跟踪较稳定。除此之外,调度周期与观测子任务时长的选取,其直接影响优化染色体规模大小,调度周期越短,观测子任务时长越长,则调度周期内的待调度任务规模就越小,从而降低染色体规模减少计算时间。但是调度周期太短,即调度策略频繁计算,会使得预警全过程中的卫星切换率大大增加,观测子任务时长太长,则会使卫星资源灵活性下 降,随着目标数量的增加,会使得目标长期无法分配观测资源,二者的确定是下一步研究的重点。

5 结 论

本文针对预警卫星低轨星座跟踪中段多目标时的传感器调度问题,建立了预警卫星低轨星座传感器资源调度混合整数规划模型,以跟踪PCRLB变化率和传感器切换率为优化指标,设计了求解调度模型的GA-SA混合优化算法,该算法结合了遗传算法优化操作简单、全局寻优能力强和模拟退火使用Metropolis准则抽样跳离局部最优的特点。仿真试验表明,本文所建立的低轨星座传感器资源调度模型和GA-SA混合优化算法是有效的,提高了调度策略计算的效率。