雷达动目标短时稀疏分数阶表示域探测方法
2018-11-09于晓涵陈小龙
于晓涵, 陈小龙, 黄 勇, 关 键, 何 友
(海军航空大学, 山东 烟台 264001)
0 引 言
受复杂电磁环境(杂波和干扰等)及目标运动类型多样性的影响,雷达对低可观测动目标的探测性能有限,难以满足实际需求[1]。具有低可观测性能的机动目标的回波信杂比(signal-to-clutter ratio, SCR)通常较低,且具有时变和非平稳特性,回波具有高阶相位和高次调频特性[2],传统的动目标检测(moving target detection, MTD)方法基于傅里叶变换实现,其形成的多普勒滤波器组仅适于分析非平稳的匀速运动目标,而具有复杂运动特性的机动目标回波,经MTD处理后的回波频谱将跨越多个多普勒单元,能量发散,难以在单一多普勒通道形成峰值,检测性能下降[3]。为此,将一维频域处理扩展为时间-频率二维处理,即时频分析,适合分析时变信号,将其用于雷达动目标检测,能够反映多普勒随时间的变化,如短时傅里叶变换(short-time Fourier transform, STFT)[4]、Wigner-Vill分布(Wigner-Vill distribution, WVD)、短时分数阶傅里叶变换(short-time fractional Fourier transform, ST-FRFT)[5]等,已用于特征提取、目标成像和识别中[6],但该类方法仍存在时频聚集程度低、分辨率有限、部分受交叉影响、运算量大等缺点,在实际工程应用中受限。此外,该类方法多为信号的匹配增强方法,时频变换需与目标运动特性相匹配,但在实际中动目标信号复杂,积累增益下降。亟需发展和研究适合高阶相位时变信号的高时频分辨率、多分量信号分析的方法和手段[6]。
由于动目标回波信号在某个域中具有一定的稀疏特性,则可将动目标检测问题转换为稀疏域中的稀疏求解和检测问题,进而通过求解最优化问题,实现稀疏域的信号高分辨率表示[7]。近年来,稀疏时频分布(sparse time-frequency distribution, STFD)引起了信号处理领域国内外专家学者的广泛关注[8-10],该方法将稀疏分解的局部优化思想与时频分析方法相结合,既能实现表示得到信号的时频分布,又能提高时变信号的时频分辨能力,因此在雷达动目标检测领域具有非常广阔的应用前景[11-13]。目前,该领域尚处于起步研究阶段,理论和应用较为完备的代表是美国麻省理工学院研究团队[14-16],2012年提出了稀疏傅里叶变换(sparse Fourier transform, SFT),并逐步发展了多个版本的快速算法。该方法克服了传统快速傅里叶变换(fast Fourier transform,FFT)算法运算量随采样点线性指数增加的不足,运算量近似保持线性增加,极大提高了大数据量条件下的运算效率,在被评为十大信息处理技术,应用于频谱感知、医学成像、图像检测和大数据处理等方面。然而,该方法不能反映信号频率随时间的变化特性,也不能处理具有高阶相位或高次调频率的机动目标的信号。
分数阶变换方法对机动目标有良好的能量聚集性和检测性能,典型方法包括FRFT[17]和分数阶模糊函数(fractional ambiguity function, FRAF)[18],能够处理加速运动目标和具有高次调频特性的机动目标,但分数阶变换方法缺少时域定位功能,不能对任意时刻信号局部频率特性分析,同时时频分辨率有限。充分利用时频分布(time-frequency distribution,TFD)和稀疏表示优化算法的优势,构建稀疏分数阶表示域理论框架,即稀疏FRFT(sparse FRFT, SFRFT)[19]和稀疏FRAF(sparse FRAF, SFRAF),并加入滑动的短时窗函数,提出短时稀疏分数阶表示域动目标探测方法(short-time sparse fractional representative domain, ST-SFRRD),即短时SFRFT(ST-SFRFT)和短时SFRAF(ST-SFRAF),在实现高分辨时变信号时频表示的同时,改善SCR,提高复杂环境下雷达机动目标检测的性能,此外,由于算法能够同步提取目标的运动特征,能够用于运动状态的分类,如匀速运动、加速运动、高阶机动等。
1 动目标时频分布模型
雷达动目标信号经过脉冲压缩后,可建模为幅度起伏的调频(frequency modulated, FM)信号,即
(1)
式中,a(tm)为信号的包络;tm为脉间慢时间;φ(tm)为信号相位。
对于动目标信号模型,其时频分布(time-frequency distribution,TFD)可表示为
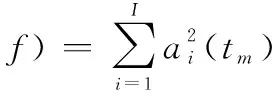
(2)

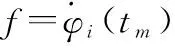

(3)
式中,f0=2v0/λ为初始频率;λ为雷达发射信号波长;v0为目标运动初速度;μs=2as/λ为调频率;as为加速度;k=2g/λ,g为急动度。此外,在长时间观测和相参积累时,动目标回波多普勒频率仍会随时间变化,具有时变特性,也可近似为高阶相位信号。
2 ST-SFRRD理论框架
信号x(tm)的TFD是在正交完备基上的分解,因此是稀疏表示的特殊情况,若分解字典为过完备字典,则TFD可推广为稀疏表示问题,其原子可由信号在TFD域中的频率估计组成

(4)
式中,ρx(tm,f)、βi(tm)、h(tm)、qi(tm,f)分别表示信号x(tm)的稀疏时频分布、稀疏分解系数(其大小表示信号与原子的相似程度)、窗函数和稀疏表示的原子;i为原子个数。
将最优化的求解思路用于解决式(5)的信号稀疏表示问题,通常所采用的方法为l1范数最小化求解,即
ρx(tm,f)‖1,
s.t.ο{ρx(tm,f)}=b
(5)
式中,ρx∈RN;b∈RK;b为实数;ο为K×N的稀疏算子。式(5)可松弛为不等约束,即[13]
ρx(tm,f)1,
s.t. ‖ο{ρx(tm,f)}-b‖2≤ε
(6)
当ο为FRFT时,b为FRFT域幅值,则式(6)表示为ST-SFRFT,即

s.t. ‖ο{Fα(tm,f)}-f(α,u)‖2≤ε
(7)
式中,α、Fα(tm,f)、u分别表示变换旋转角、ST-SFRFT时频分布和ST-SFRFT域

(8)
Kα(τ,u)=
(9)
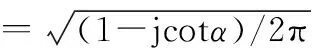
(10)
当ο为FRAF时,b为FRAF域幅值,则式(6)表示为ST-SFRAF

s.t.‖ο{Rα(tm,f)}-f(α,u)‖2≤ε
(11)
式中,Rα()为ST-SFRAF算子;α为旋转角;u为ST-SFRAF域。
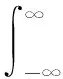
(12)
Rx(τ,κ)定义为瞬时自相关函数(Instantaneous ACF, IACF),表示为
Rx(τ,κ)=x(τ+κ/2)x*(τ-κ/2)
(13)
式中,κ为回波信号时延,对于固定距离单元的回波数据,时延κ为固定常数。
3 ST-SFRRD动目标检测方法
ST-SFRRD动目标检测和参数估计算法的流程图如图1所示。

图1 ST-SFRRD雷达动目标探测方法流程图Fig.1 Flowchart of the ST-SFRRD-based radar moving target detection method
包括如下几个步骤:
步骤1雷达回波匹配滤波处理
步骤2稀疏时频分析参数初始化
(1) 短时窗函数、窗长度选取
窗函数可选取矩形窗
h(τ)=1,|τ|≤Tn
(14)
式中,Tn为窗长度,也可采用高斯窗函数,即

(15)
式中,σ为标准差,可通过调整该参数改善信号的频率分辨率。
(2) 稀疏分解字典设计
在雷达发射单频信号或LFM信号的前提下,动目标多普勒频率与速度近似成正比,在较短的观测时间范围内,可采用调频信号作为复杂机动目标信号的近似。因此,可采用LFM或QFM基构造稀疏分解字典,GL×M、QL×M,即
(17)

步骤3动目标回波高分辨稀疏时频表示和优化求解
进行式(6)~式(13)所示的ST-SFRRD运算,采用式(16)和式(17)所述的过完备字典作为ST-SFRRD的稀疏分解字典,并采用凸优化理论的基追踪降噪法(basis pursuit denoising, BPDN)对式(6)进行求解[20]

(18)
另外,也可借鉴SFT的思路,将SFRFT和SFRAF中的傅里叶变换过程用SFT替换,提高ST-SFRFT的运算效率[14]。
步骤4ST-SFRRD动目标检测
对于建模为LFM或QFM的机动目标信号将在ST-SFRRD表现为一峰值,将ST-SFRRD域幅值作为检测统计量,与检测门限进行比较,并记录超过门限的最大峰值坐标
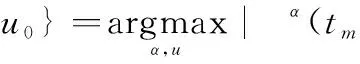
(19)
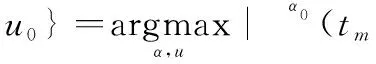
(20)
式中,η为检测门限,继续计算不同时间窗最佳变换角α0条件下的ST-SFRRD,从而得到不同时刻信号的瞬时频率。
对于建模为QFM的机动目标信号
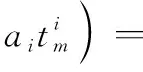

(21)
式中,ai(i=1,2,3)表示多项式系数,其IACF表示为

(22)
采用矩形窗函数h(τ)=1,得到机动目标信号的ST-SFRAF表达式为

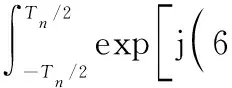
(23)
当12πa3κ+cotα=0时,式(23)转变为sinc函数,即

Tnsinc[(4πa2κ-ucscα)Tn/2]
(24)
由此可知,单分量机动目标信号在ST-SFRAF域表现为一峰值,峰值坐标为
(α0,u0)=[arccot(-12πa3κ),4πa2κsinα0]
(25)
步骤5目标运动参数估计
对于匀加速运动目标,将在ST-SFRFT域能量得到最佳积累,则峰值坐标可用来估计目标的加速度和初速度运动参数
(26)
对于变加速时或高阶机动目标,将在ST-SFRAF域能量得到最佳积累,则峰值坐标可用来估计目标的急动度和加速度运动参数
(27)
信号的初始频率f0可通过对原始信号进行dechirp运算,并搜索FFT后的峰值估计得到
(28)
4 实测数据验证与分析
采用不同波段的对海雷达实测数据验证所提的基于ST-SFRRD的雷达动目标检测技术。南非科学与工业研究中心(centre of scientific and industrial research, CSIR)X波段CSIR对海雷达数据库采用相参体制的Fynmeet雷达采集[22],选取海况等级为4级的TFC17-002数据作为验证数据,对海探测试验雷达配置及环境参数如表1所示。图2给出了CSIR对海雷达动目标探测试验数据描述,分别为雷达回波距离-时间图(图2(a))和目标单元(距离单元25和26)的时频分布(见图2(b))。可以看出,目标具有机动特性,其回波多普勒呈现明显的时变特性,并且海杂波较强,与动目标频谱有部分重叠,严重影响了雷达对动目标的探测。

表1 CSIR对海探测试验参数(2006.08.03)
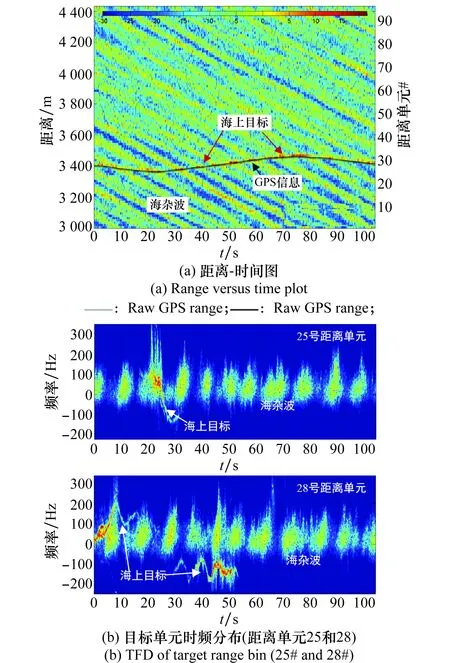
图2 X波段CSIR对海雷达动目标探测试验数据描述(TFC17_002)Fig.2 Description of moving target detection dataset with X-bandCSIR radar (TFC17_002)
根据全球定位系统(globle position system,GPS)数值取出动目标雷达回波数据进行分析,图3为起始时间26 s的动目标STFT时频分布,可以看出,在较短的观测时间范围内,动目标的多普勒呈现线性调频分布,其频谱幅度低于海杂波频谱,使得动目标检测性能下降。基于高分辨短时稀疏时频表示的处理结果如图4所示,该段时间内,动目标回波可由LFM近似,通过对比可知,提出的ST-SFRFT性能优于传统变换域处理技术,目标峰值凸显,杂波虚警较少,提高了雷达的检测概率。估计目标径向运动参数为v0=2.67节(海里/时)、as=0.83 m/s2。
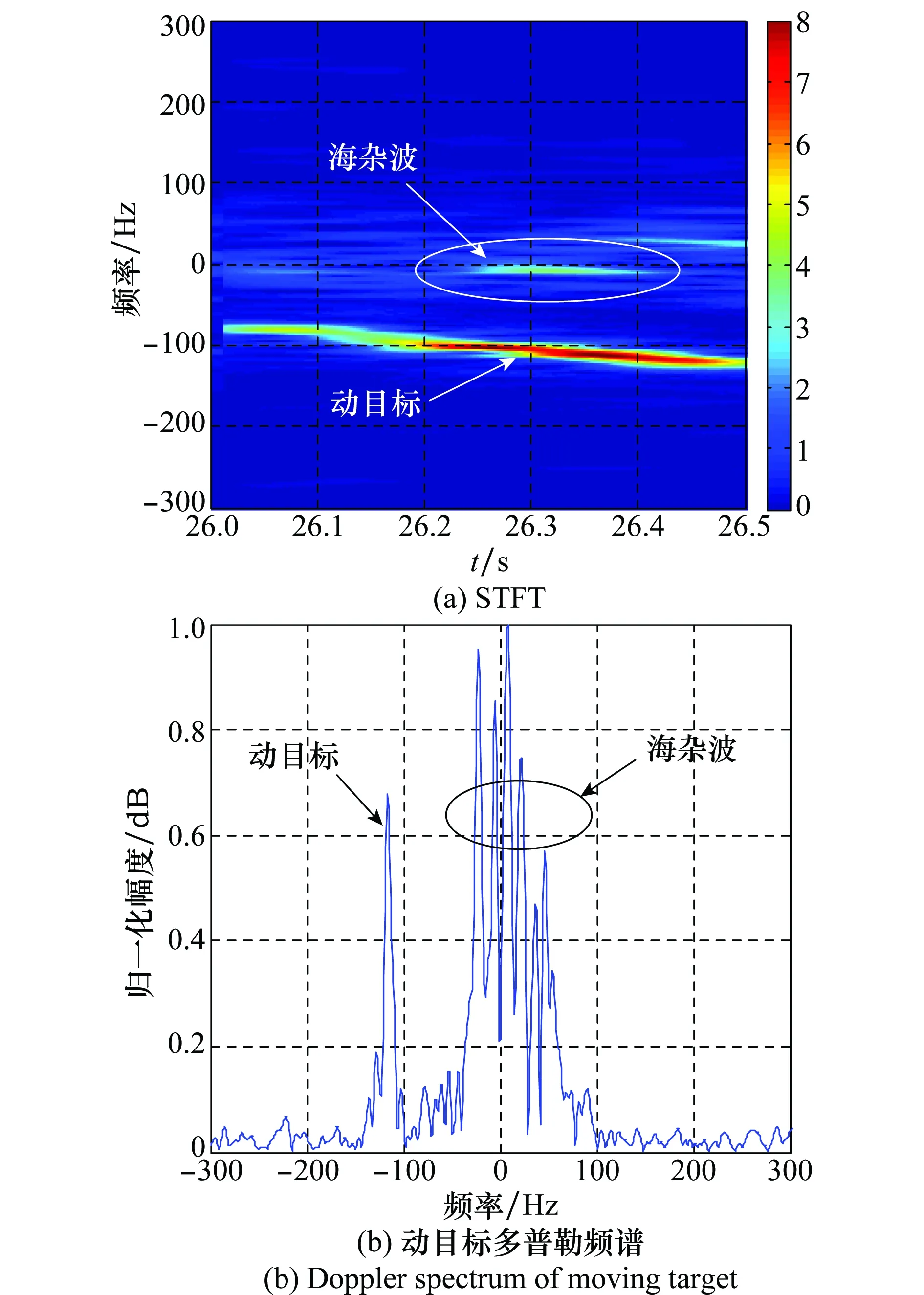
图3 海上动目标信号STFT时频分布(起始时间=26 sFig.3 STFT distribution of marine target (starting time=26 s)
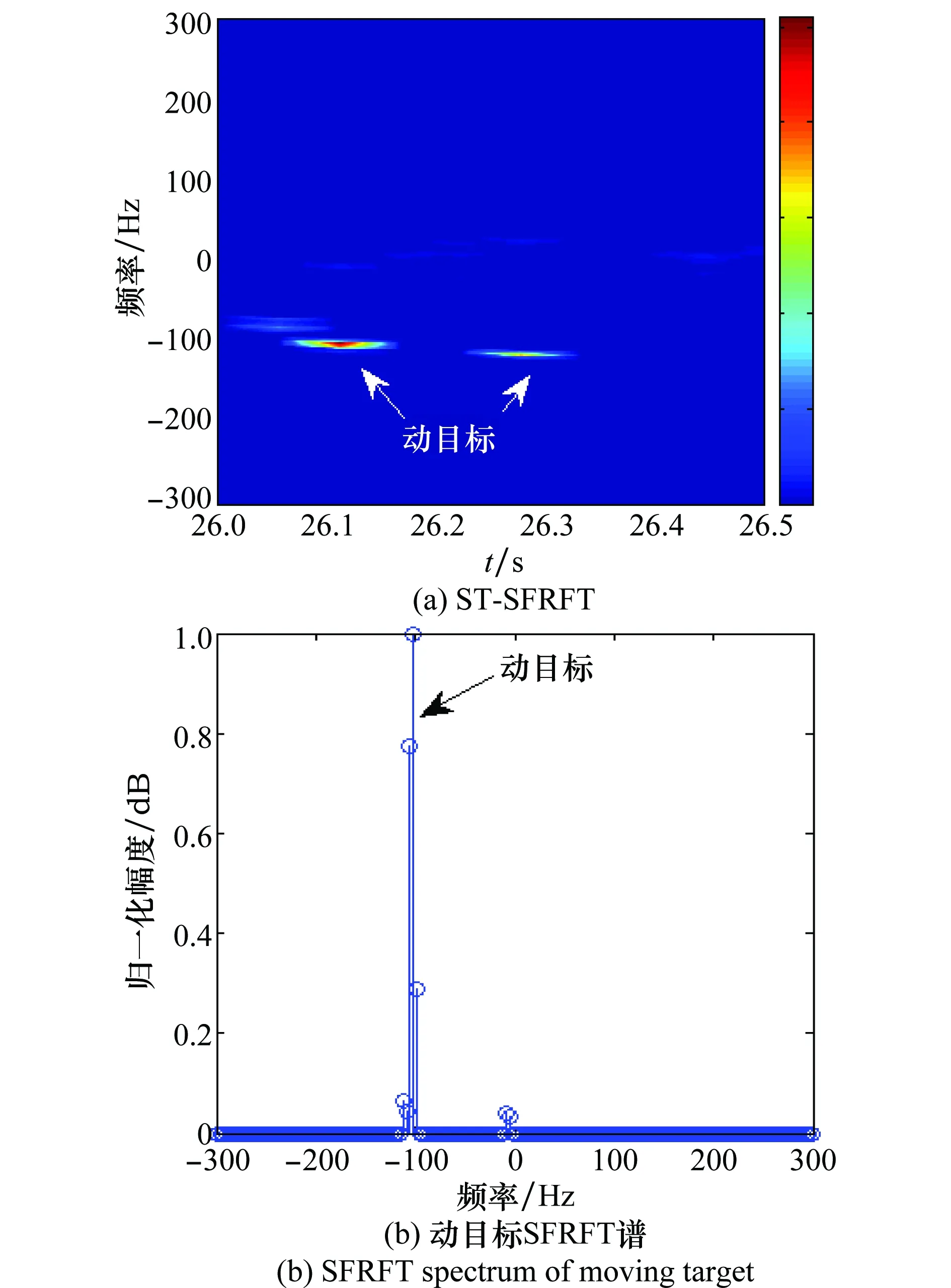
图4 海上动目标信号ST-SFRFT分布(起始时间=26 s)Fig.4 ST-SFRFT distribution of marine target (starting time=26 s)
采用S波段对海雷达数据验证所提算法,分别选取两种运动类型的海上目标回波数据作为待检测数据,海况等级均为高海况,图5给出了S波段对海雷达动目标回波距离-多普勒分布,通过船舶的船舶自动识别系统(automatic identification system, AIS)信息可知,在74.2 nm和34.8 nm附近分别有一货船和海事巡逻船,但受强海杂波以及距离远的影响,目标回波较为微弱,在时域和频域发散,传统的时域幅度检测或频域检测难以发现目标。

图5 S波段对海雷达动目标回波距离-多普勒分布Fig.5 Range-Doppler plot of marine moving target using S-band radar
分别采用STFT和提出的ST-SFRRD方法对两种目标进行处理,图6和图7分别给出了两个运动目标的不同表示域处理结果对比。由图6(a)可知,动目标1的频谱淹没在海杂波谱中,且多普勒谱发散,说明目标多普勒具有时变特性,而STFT方法基于传统的傅里叶变换,难以有效积累时变信号,导致积累增益低,SCR改善不明显。图7(a)可以看出,动目标2的频谱具有高阶调频特性,说明目标机动,但海杂波和噪声仍然影响目标检测,虚警偏多。针对两类目标的不同的运动特性,分别采用ST-SFRFT和ST-SFRAF方法进行处理,得到如图6(b)和图7(b)所示的结果,对比STFT方法,表明所提方法具有较高的时频分辨率,目标谱峰特征明显,在实现信号能量聚集的同时,得到了动目标信号的高分辨时频表示;同时,极大改善了雷达对目标运动参数的估计能力,根据ST-SFRRD的稀疏分解系数可估计出目标的运动瞬时速度和加速度,分别为动目标1:v0=11.64 m/s,as=3.64 m/s2;动目标2:v0=5.16 m/s,as=0.92 m/s2。因此,采用ST-SFRRD在实现对机动目标时变多普勒特征描述的同时,获得了高分辨的参数估计性能,从而对雷达提高低可观测动目标的检测和参数估计能力提供了一种有效途径。

图6 海上动目标1不同表示域处理结果对比Fig.6 Detection results of marine moving target 1 in different representative domains

图7 海上动目标2不同表示域处理结果对比Fig.7 Detection results of marine moving target 2 in different representative domains
为进一步定量说明所提方法在SCR改善方面的优势,采用文献[22]定义的表示域SCR,得到如表2所示的性能比较结果。可知,所提算法能够极大地增加动目标与海杂波的峰值差,改善输出SCR,但由于ST-SFRRD类方法需要进行稀疏优化求解以及字典的构建和搜索,运算时间明显长于STFT方法,下一步将研究基于SFFT实现的快速ST-SFRRD方法,提高运算效率。

表2 不同表示域处理方法性能比较
5 结束语
本文结合时频分布技术和稀疏表示优化算法的优势,构建了ST-SFRRD信号处理框架,并在此基础上,提出了两种雷达机动目标检测和分类方法,即ST-SFRFT和ST-SFRAF变换技术,加入滑动的短时窗函数,实现了时变信号的时间-稀疏变换域高分辨表示。实测雷达数据验证表明,所提方法能够提高机动目标信号的能量聚集和时频分辨率,显著改善雷达机动目标检测和参数估计能力。后续将研究基于SFT的ST-SFRRD快速实现方法及工程应用。
