具有连续转轴的新型3-UPU 并联机构的运动特性分析

2018-11-09韩雪艳王子义李仕华田志立

中国机械工程 2018年20期

韩雪艳王子义李仕华田志立

1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，066004

2.燕山大学机械工程学院，秦皇岛，066004

0 引言

具有两转动一移动的三自由度并联机构（2R1T）是非常重要的一类构型，应用于诸多领域。2R1T并联机构的转轴在空间的分布对机构的标定和轨迹规划十分重要［1］，但现有大多数的2R1T并联机构在转动过程中轴线不固定，即转轴为瞬时转轴，为其标定和轨迹规划带来了不便。

很多学者对机构转轴进行了研究。李秦川等［1］通过分析机构发生转动后其约束螺旋的变化分析了2⁃UPR⁃SPR并联机构的连续转轴。LIU等［2］采用在分支中添加平行四边形复合运动副的方法构造了一类具有很强的转动能力的三自由度并联机构。XU 等［3⁃4］采用螺旋理论对一种 2⁃RPU/SPR两转一移并联机构的连续转轴进行了研究，并基于具有连续转轴的2R1T并联机构构造了一种五自由度混联机构。LI等［5］采用在3T1R并联机构中添加冗余支链的方法得到了很多冗余驱动并联机构。窦玉超等［6］提出了一种两转动一移动自由度的完全解耦并联机构，并对其工作空间、奇异性进行了分析。LI等［7］分析了 3⁃［P］［S］类并联机构的转轴的分布情况。陈子明等［8⁃11］提出了一类无伴随运动的对称两转一移并联机构，该类机构可以绕中间对称平面内任一条直线做连续转动。

上述研究要求机构动定平台或运动副轴线具有特殊的位置关系，在实际应用中很难保证，不利于机构的应用。本文提出了一种新型的3-UPU空间对称的并联机构，并对机构的自由度、运动特性和工作空间进行了分析。

1 初始位形下机构自由度分析

1.1 机构构型

如图1所示，新型3-UPU机构是由2个全等的正三角形平台和3条完全相同的UPU分支组成。每个UPU分支包含2个万向铰链（Ui，i=1，2）以及1个移动副（P副）。每个U副由2个垂直相交的转动副构成，其中与平台相连的转动副称为Ui的第一转动副（Ui1），与中间移动副相连的转动副称为Ui的第二转动副（Ui2）。U11、U21以一定角度对称倾斜布置在动定平台上，且其轴线相交于中间对称平面S内一点P1，U12、U22以相同角度与中间移动副倾斜相连且其轴线交于中间对称平面S内一点P2。在初始位形下，中间移动副与上下平台垂直，且任意位形下均与中间对称平面S保持垂直。

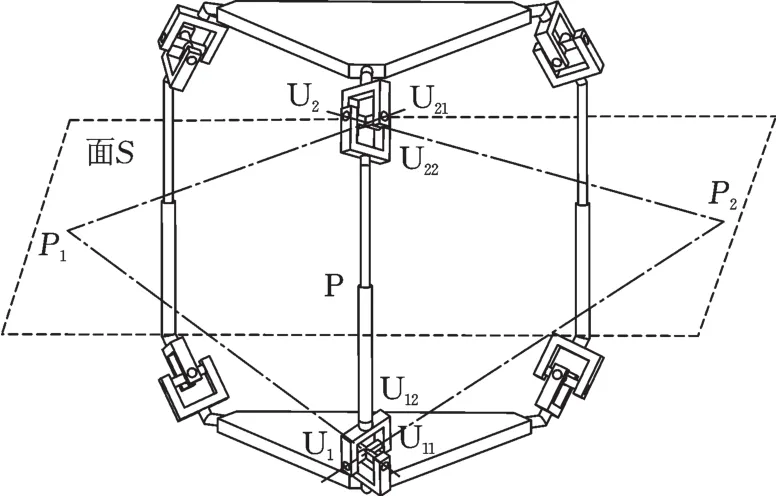
图1 3-UPU机构示意图Fig.1 Schematic diagram of 3-UPU

1.2 机构自由度分析

根据螺旋理论［12］可知

由式（1）可以得到：①分支约束力与分支转动副轴线共面（相交或平行），并且分支约束力与分支中的移动副轴线垂直；②分支约束力偶方向与分支所有转动副轴线垂直，约束力偶的方向与移动副轴线几何关系可以是任意的。

机构单个分支的布置见图2。

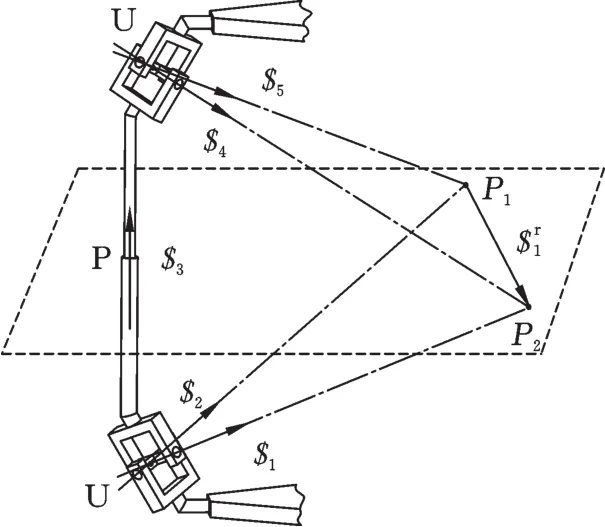
图2 UPU分支Fig.2 UPU branch

根据螺旋的互逆性，UPU分支约束螺旋与分支所有转动副轴线共面（相交或平行），同时与分支中所有移动副轴线垂直，因此约束螺旋只有1个，即通过2个交点P1和P2的约束力螺旋＄r1；UPU分支约束力偶的方向与分支所有转动副轴线垂直，因此约束力偶不存在。UPU分支具有1个过转动副轴线交点P1、P2的约束力，且其分布在中间对称平面内。

由于机构分支采取对称布置，故对平台所施加的约束力＄ri（i=1，2，3）相互交错，且位于中间对称平面内，见图3。

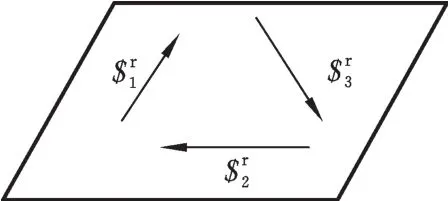
图3 约束力矢量图Fig.3 Vector diagram of the constraining screws

3个约束力＄ri（i=1，2，3）限制了动平台沿对称平面方向的2个移动自由度和对称平面法线方向的转动自由度，机构具有3个自由度，即在对称面上的2个转动自由度和沿对称面法线方向上的1个移动自由度。

1.3 自由度数的验证

根据修正Kutzbach⁃Grubler公式［12］来计算自由度：

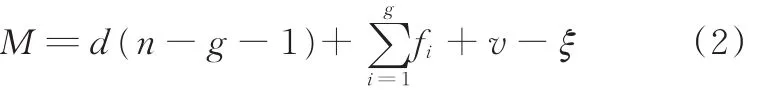
式中，d为机构的阶数；n为机构的构件数；g为机构的运动副数；fi为第i个运动副的自由度数；v为机构的冗余约束数；ξ为机构的局部自由度数。

该机构公共约束个数为0，机构的阶数d为6；机构构件数目n为8；运动副个数为9，其中6个U副具有2个自由度，3个移动副具有1个自由度；机构冗余约束v的个数为0；局部自由度ξ为0。因此，机构自由度为

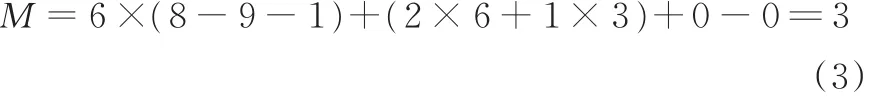
2 机构自由度的非瞬时性分析

利用单叶双曲面的相关性质证明当机构发生运动后，该机构始终关于中间平面对称，且其自由度始终为2R1T，即自由度具有非瞬时性。

2.1 单页双曲面的性质

如图4所示，直线l绕与它不共面的直线k旋转而成的曲面称为单叶双曲面。这种由一族直线所构成的曲面称为直纹曲面，而构成直纹曲面的那族直线称为直纹曲面的一族直母线。单叶双曲面的两族母线具有如下特性：①单叶双曲面上异族的任意两条直母线必共面（相交或平行），而同族的任意两条直母线必为异面直线；②单叶双曲面上的任意母线与主轴线的距离相同，与主轴线的夹角相同；③与主轴线距离和夹角相同的直线为同一单叶双曲面的直母线。

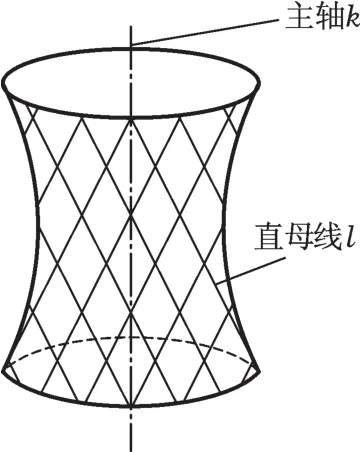
图4 单叶双曲面示意图Fig.4 Schematic diagram of single leaf hyperboloid

2.2 机构在任意位形下的对称性分析

首先，讨论分支的对称性。如图5所示，在初始位形下，每个分支的 U12、U22转动副轴线 l1、l2关于中间对称平面S1对称，且相交于平面S1上一点P2，移动副轴线lp垂直于平面S1。当机构发生转动或移动时，U12、U22转动副之间只发生沿移动副轴线lp方向的移动，所以机构位形发生变化时，这两个转动副将始终关于一个分支平面对称，相交于平面上一点移动副轴线lp始终与该平面保持垂直状态。

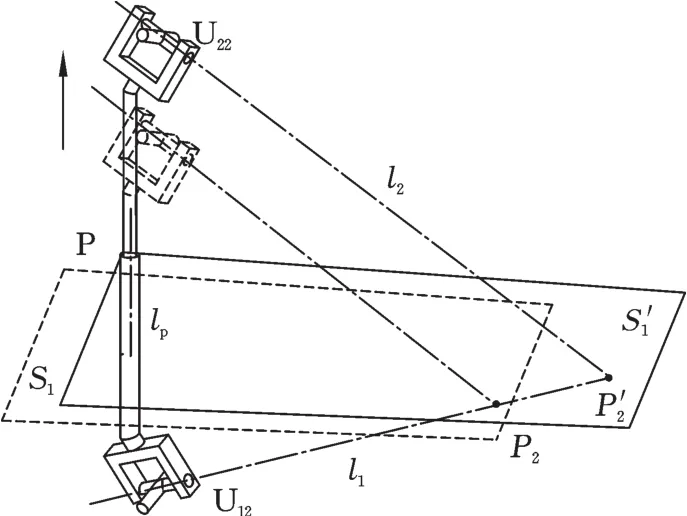
图5 分支对称平面Fig.5 Branch symmetric plane

其次，讨论动定平台的对称性。在初始位形下，动定平台关于平面S2对称，见图6。分支与定动平台连接的转动副的轴线l3、l4关于平面S2对称，相交于平面上P2点，且l3、l4到平面S2上任意直线k的距离和夹角相同。

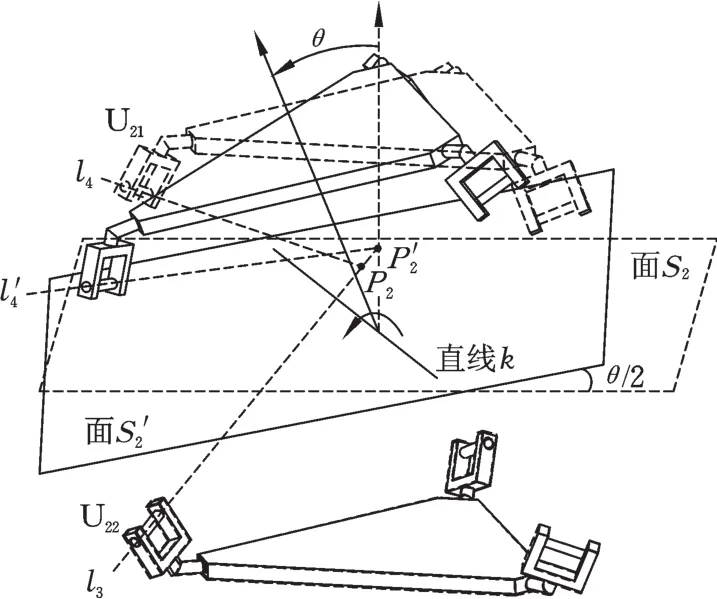
图6 动定平台旋转前后的位形Fig.6 The position of the moving and fixed platform before and after rotation

同理，与动定平台相连的另外2个分支上的2组转动副轴线也是彼此相交的。机构转动后，由于动定平台结构上镜面对称，而且固连其上的3个分支的U11、U21转动副的3对轴线彼此相交，因此动定平台关于某一平面对称，该平面由3对轴线的交点确定，且该平面相当于原中间对称平面绕直线k转动θ/2。

此外，当动平台发生沿对称平面法线方向移动时，动定平台关于中间平面对称，其正确性显而易见，在此不再赘述。

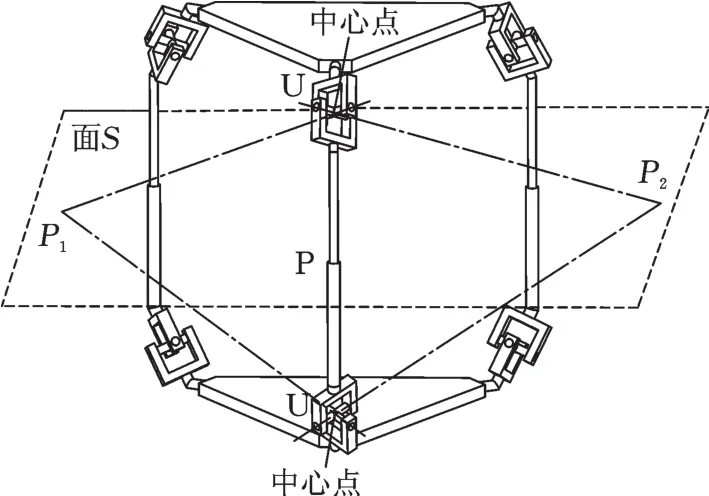
图7 3-UPU并联机构Fig.7 3-UPU parallel mechanism

最后，讨论机构的对称性。如图7所示，由于每个分支中的U1、U2副的中心点（U副两个转动副轴线的交点）始终关于分支对称平面S1（或）对称，也始终关于动定平台对称平面S（2或）对称，且两点间的对称平面只有1个，所以2个对称平面S1（或）、S（2或）为同一平面S。因此，机构在任意位形下，均存在1个中间对称平面S，且每个分支的上下2组U副转动副的轴线始终对称且相交于中间对称平面S上的P1、P2点，移动副的轴线始终垂直于中间对称平面S。

2.3 机构自由度非瞬时性

根据前述分析，在初始位形下，机构的每个分支均存在1个约束力，分布在中间对称平面S内且通过2个运动副的交点。3个约束力均交错分布在中间对称平面内且通过各分支的2个运动副交点，限制了动平台沿平面S上的2个移动自由度和对称平面法线方向上的转动自由度，使得机构只具有绕中间对称平面内直线转动自由度与垂直于中间对称平面移动自由度。动平台发生上述3种运动后，由前述论证可知，机构的3个约束力仍分布在中间对称平面内且通过各分支的2个运动副交点，因此，机构自由度是非瞬时的。

3 机构连续转动特性分析

3.1 机构连续转轴位置确定

初始位形下，该机构可以绕中间对称平面S内任意一条直线做瞬时转动，且机构发生转动后仍关于某一中间平面S′对称，仍然具有绕平面S′上任意直线做瞬时转动的能力；机构转动前后，转动轴线始终位于对称平面内，所以可以绕对称平面内同一条直线连续转动。同理，转动后的中间对称平面内所有直线均作为机构继续转动的连续转轴。

信号参数如表1所示。在这个信号中,基波、2次谐波和3次谐波附近都存在一个间谐波,如果直接使用加窗插值FFT算法进行处理,上述分量将难以被区分出来,计算结果误差会很大。为了避免这种情况,在计算信号参数前使用本文方法来处理待测信号。

此外，由于机构动平台沿着对称平面S的法线移动后，动定平台的姿态均未改变，移动前后机构对称平面S仍相互平行，故约束力仍位于移动后的机构对称平面内，动平台仍可沿着该方向移动，即机构的移动也是连续的。

综上，该机构的运动特性为：动平台可以绕机构中间对称平面上的任意一条直线连续转动，或沿垂直于中间对称平面方向连续移动。当动平台转动或移动后，动平台仍可绕着新的中间对称平面内的任意一条直线转动或沿垂直于新的中间对称平面的方向移动。所以该机构对称平面上的任一直线皆为连续转轴。

3.2 连续转动的仿真验证

采用SolidWorks建立机构仿真模型，验证其可在任意位形下绕中间对称平面上的任一直线做连续转动。

在初始位形下，如图8所示，选取中间对称平面内任一直线k1作为转动轴线，并在此轴线处搭建1个分别与动定平台固连的中间转动副，在其上添加旋转马达，驱动动平台绕该轴线连续转动一定角度θ1（取θ1=20°）。提取3个移动副的位置参数数据，并作为驱动添加到机构的3个移动副中，见图9；动平台中心点P运动到P′点轨迹是一段绕所选轴线的圆弧，所以在初始位形下该机构可以在移动副驱动下绕中间对称平面内任一直线做连续转动。

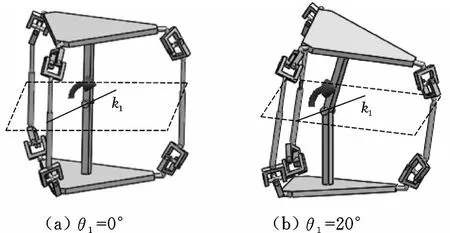
图8 初始位形下以中间转动副驱动机构Fig.8 The mechanism driving by middle rotational pair under the initial position

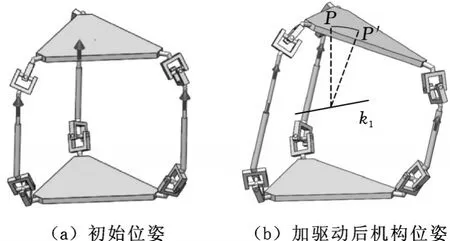
图9 初始位形下以移动副驱动机构Fig.9 The mechanism driving by prismatic pair under the initial position

同理，在动平台运动后，重复上述过程，驱动动平台绕新对称平面内任意轴线k2旋转一定角度θ2（本文取θ2=20°），见图10。如图11所示，动平台中心点P′运动到P″点，经验证其轨迹为一段绕所选轴线的圆弧，所以在任意位形下该机构可以在移动副驱动下绕中间对称平面内任一直线做连续转动。根据上述仿真结果，该机构可实现连续转动。

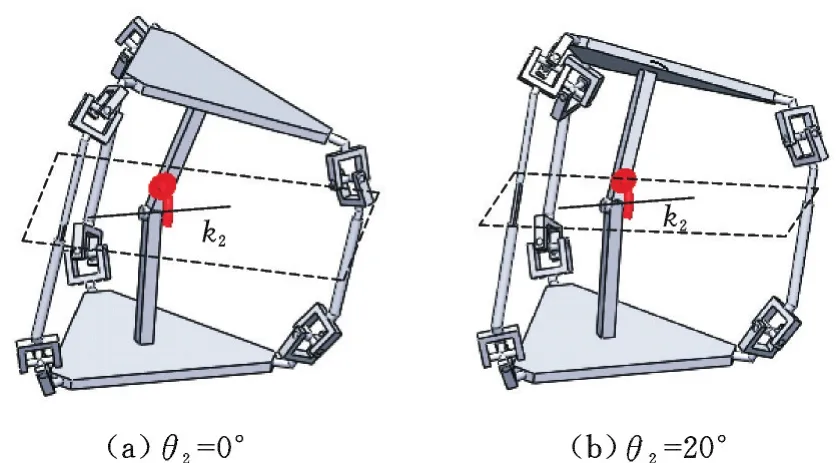
图10 转动后以中间转动副驱动机构Fig.10 The mechanism driving by middle rotational pair after rotation

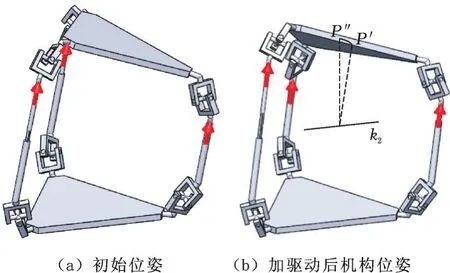
图11 转动后以移动副驱动机构Fig.11 The mechanism driving by prismatic pair after rotation

4 机构运动学反解及工作空间分析

4.1 机构运动学反解分析

4.1.1 转动角度分析

如图12所示，初始位形下，O、O1分别为定平台、动平台中心点，O2为平面S2上的一点，OO2、O1O2分别与中间对称平面S2的夹角相同且设为α。假设动平台绕平面S2内一条直线k转动β角时，平面S2转动了γ角，因OO2和O1O2与中间对称平面的夹角仍然相同，可得

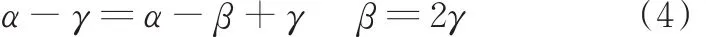
因此，在动平台旋转过程中，动平台绕转轴转过角度是中间对称平面S绕转轴转过角度的2倍。

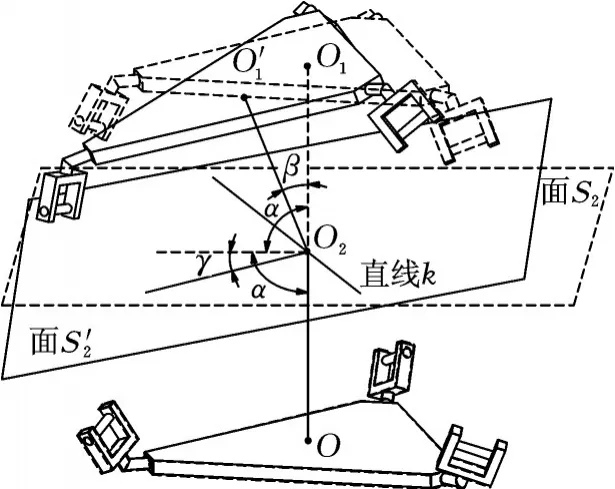
图12 机构转动角度关系图Fig.12 The relation chart of rotation angle

4.1.2 位置反解

如图13所示，在动定平台和中间对称平面上分别建立坐标系，其中，A1、A2、A3为与定平台相连U1副的中心点，a1、a2、a3为与动平台相连U2副中心点。定系OXYZ的原点O在定平台中心，X轴垂直于A1A3指向A2方向，Z轴垂直于定平台且指向上方，Y轴按照右手定则确定；动系O1X1Y1Z1在动平台上的布置与定系OXYZ在定平台上的布置相同；与中间对称平面S固定的坐标系O2X2Y2Z2的各个轴线在初始位形下与定平台各坐标轴平行。

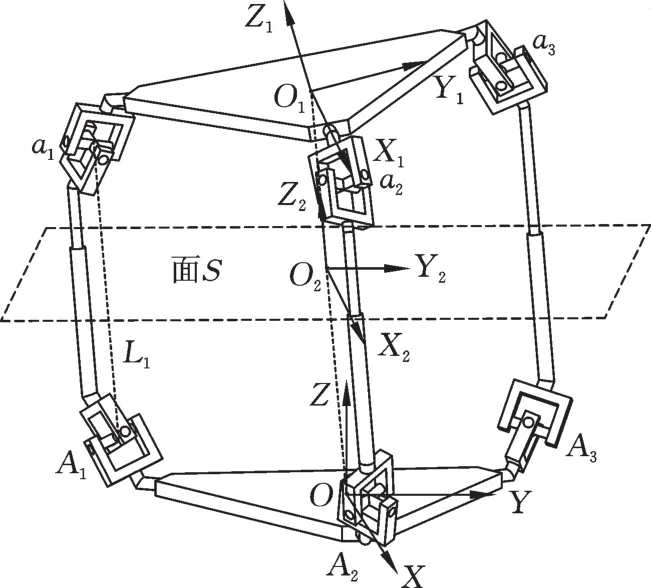
图13 机构的坐标系Fig.13 The coordinate system of the mechanism

由于动定平台关于中间对称平面对称，动平台运动时定系坐标原点O到动系坐标原点O1的向量始终为中间对称平面的法向量，因此当动平台中心点O1已知时，中间对称平面的姿态也可以确定。平面S的姿态矩阵可以采用绕着坐标系O2X2Y2Z2旋转的xyz型欧拉角（α，β，γ）来表示。受机构的约束力的限制，平面S只能绕着X2、Y2轴转动，不能绕着Z2轴转动，故γ=0，因此平面S的姿态矩阵T′为

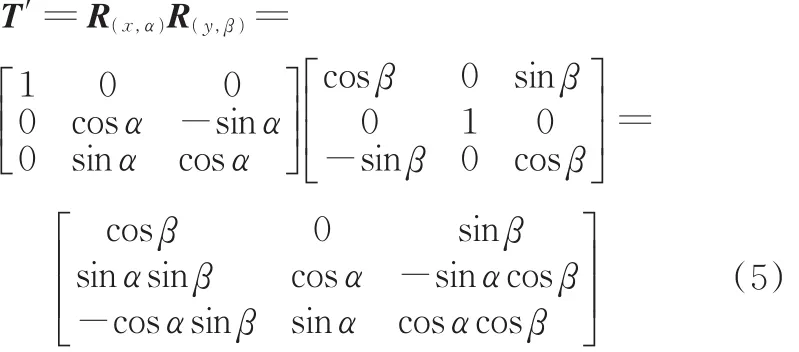
当已知动平台中心点O1在定系中的坐标(x,y,z)T时，中间对称平面的单位法向量为

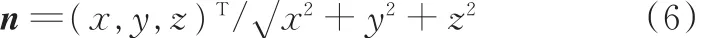
结合平面S的姿态矩阵T′，可得

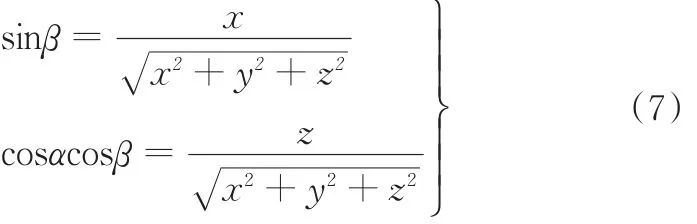
求解式（7）可得

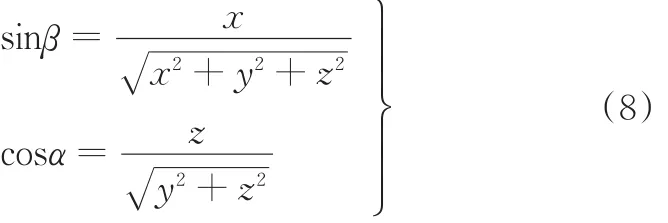
由转角分析可知，动平台转动角度为中间对称平面转动角度的2倍，动平台的姿态矩阵T可以表示为

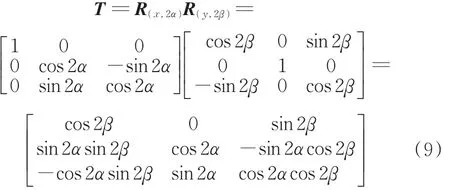
其中，姿态角α、β为动平台姿态角的1/2，而动平台姿态角的范围是(-π,π)，则α、β取值范围是(-π/2,π/2)。

当已知动平台中心点O1在定系中的坐标时，可得到动平台的姿态矩阵，动系中任意一点P在定系中的坐标P(0)即为

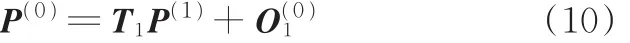
式中，P(1)为任意一点P在动系中的坐标。

从而可解得动平台U2副中心点在定系中的坐所以可以求得该机构的反解即各移动副的长度

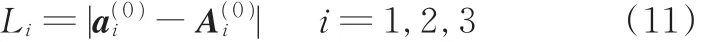
4.2 机构工作空间分析

为了更方便应用，机构采用悬吊方式，定平台固定于横梁上，并改进机构布置，扩大了移动副的移动范围及U副的转角范围，见图14。以电动缸作为机构的P副，制作了实验样机，见图15。

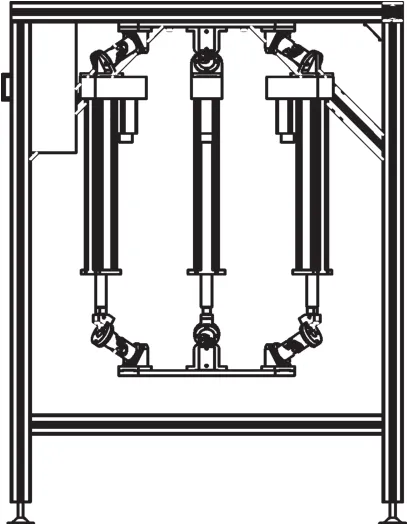
图14 改进的机构简图Fig.14 Improved mechanism diagram

图15 改进后机构实验样机Fig.15 Improved experimental prototype

采用动平台中心点O1在定系中的位置坐标(x,y,z)能达到的范围来表示其工作空间。设机构的结构参数及输入参数范围：定平台3个U副中心间的距离a=414 mm；移动副的移动范围为0～300 mm；当移动副处于零值时，机构动定平台的中心距离为290 mm；U副的转角范围是在母线与中心线夹角为60°的圆锥形范围内（由于初始位形下P副所在连杆轴线垂直于定平台，故P副轴线的转角范围也是与初始位形成60°的圆锥）。机构各分支始终相互平行，不存在分支干涉，只考虑杆长及转角限制。通过MATLAB编程，绘制机构的工作空间见图16。

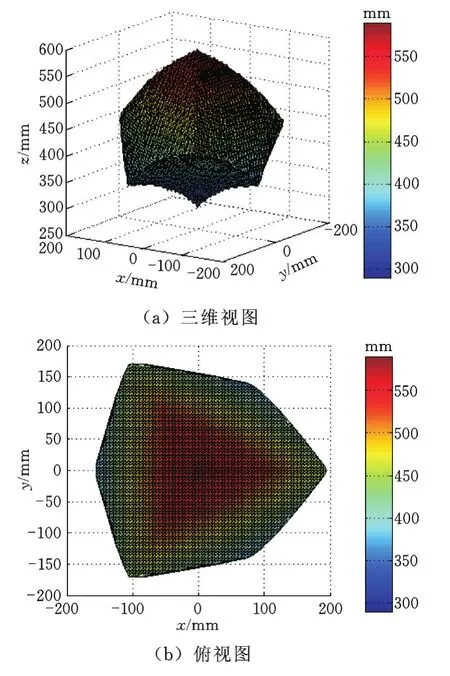
图16 3-UPU机构工作空间Fig.16 Workspace of 3-UPU parallel mechanism

由图16可知，3-UPU机构的工作空间外形近似呈对称六面体形状。Z方向的范围与P副的移动范围相同。在垂直于Z轴的平面上，沿着分支方向的可达范围最大。在Z为350～450 mm的范围内工作空间较大，且在垂直于Z轴的平面内沿着各方向的变动较小。由上述分析可知，该机构的工作空间相对较大，且呈对称分布，具有较好的应用价值。