基于离散单元法的铝粉冲击加载过程三维数值模拟
2018-11-09罗晓龙田始军
罗晓龙 刘 军 田始军 林 立 周 纯
宁波大学机械工程与力学学院,宁波,315211
0 引言
高速压制(high velocity compaction,HVC)[1⁃3]技术是一种新型的粉末成形技术。高速压制技术[4]通过液压驱动的重锤产生高频的冲击波,在0.02 s内将压制能量从压机传递到粉末压坯,从而实现致密化。因此,金属粉末在冲击加载条件下的动态响应是该技术的主要难点及热点。
离散单元法(discrete element method,DEM)最先用于分析研究岩土力学的相关问题,目前已广泛应用于不同领域[5⁃7]。近年来,随着三维离散元仿真技术的发展,许多领域的学者对三维离散元的应用进行了尝试,并取得显著成果。在粉末冶金领域,MARTIN等[8⁃9]利用离散元原理模拟了冷等静压和闭模压制条件下,粉末颗粒的重排和不同颗粒硬度复合材料的压实过程。SADD等[10]应用离散元理论对颗粒物质中应力波的传播进行了分析。郑洲顺等[11⁃13]根据离散元原理对粉末的高速压制过程进行了一系列模拟,并取得很多成果。胡仙平等[14]利用PFC2D软件,对碰撞过程中颗粒间的触力传递及颗粒排列过程进行了研究,发现在压制过程中颗粒会在自身位置的微小区域内振动并转动。
目前,基于离散元原理对粉末冲击压制过程的模拟多限于二维平面模型,而实际情况下,颗粒的配位要比二维接触中复杂得多。本文基于离散元原理,尝试利用PFC3D软件对粉末单次冲击加载过程进行三维模拟,对模拟结果与实验所测透射波波形进行对比,并利用模型模拟金属粉末的单次加载过程,对颗粒的运动情况进行了动态分析。
1 离散元数学模型
离散元原理是:把被研究系统当作由众多能独立运动的离散性单元构成的系统,每个单元都具有一定的几何特性和物理特性,单元的运动规则遵循经典力学理论,每个单元都只能与相邻的单元发生作用,材料整体的变化可由各单元之间的力与位移的关系求出。
相互接触的2个颗粒的相对位移U可在自然轴系上被分解为法向分量un和切向分量us:

其中,n、τ分别表示法向和切向的单位矢量。因此可以确定颗粒的相对位移在法向和切向的分量:

进而确定2个颗粒的相对速度在法向和切向上的分量:

PFC3D软件使用的平行约束线性方程将一组具有恒定的法向刚度和切向刚度的弹性弹簧均匀地设定在两球之间的圆形接触面上,并将应力集中在接触点。当相接触的2个颗粒发生相对运动时,这些相互平行的电接触弹簧可以传递力和转矩。根据Cundall建立的数学模型[11],作用点上线性部分的作用力F同样可分解为法向分量Fn和切向分量Fs:

模型结构如图1 所示,gr为参考缝隙,kn、ks分别为法向和切向的刚度,βn、βs分别为法向和切向的阻尼系数,µ为摩擦因数。当实际缝隙gc<gr时,碰撞发生。
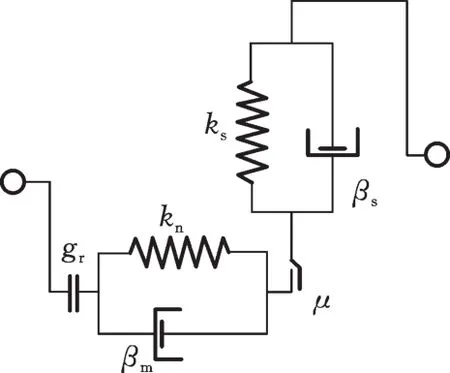
图1 弹簧阻尼并联模型Fig.1 Model of the force-displacement relationship
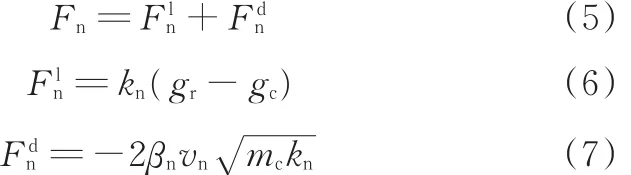
由图1可以看出,法向分量由线性弹簧力和阻尼力两部分构成:
式中,mc为有效惯性质量,由相互撞击的两球质量ma、mb决定,mc=mamb/(ma+mb)。

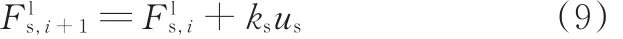
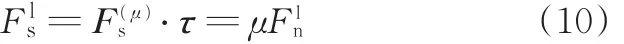
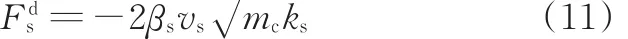
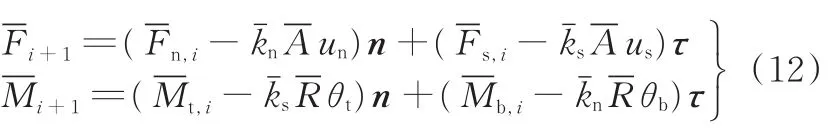
式中,kˉs、kˉn分别为平行约束中法向和切向的刚度系数ˉ为两球重叠部分截面圆形的面积;Rˉ为截面圆的半径;θt、θb分别为扭转和弯曲的相对角度。
通过式(2)~式(12)可以建立力与位移、力矩与角位移的关系。
2 实验方案
实验材料为-100目铝粉,其成分见表1。由于分离式霍普金森压杆实验设备为卧式安置,不适用于离散材料的实验,因此根据本次实验设备的尺寸设计了粉末套筒,套筒内径为14.6 mm,外径为20.6 mm,与入射杆、透射杆均属于间隙配合,如图2所示。使用JM⁃B电子天平称取粉末1 g。

表1 铝粉中各成分的质量分数Tab.1 Content of aluminite powder %
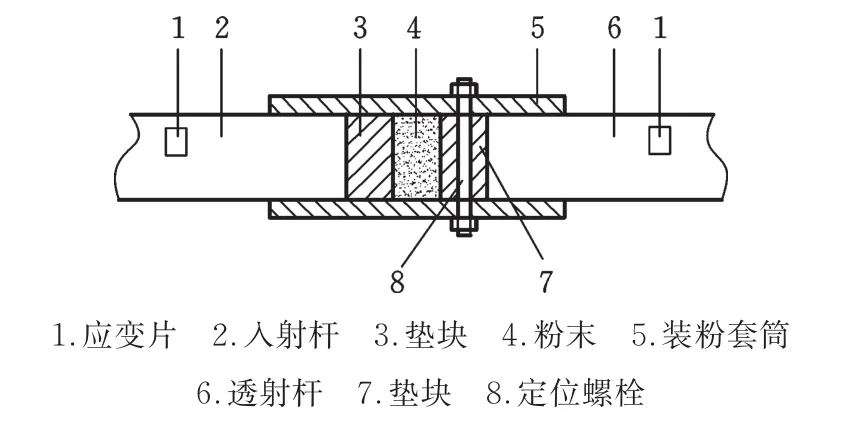
图2 粉末装粉装置Fig.2 Device for filling powder
采用ϕ14.5 mm分离式霍普金森压杆测试系统对预压后的粉末进行冲击撞击,入射杆长1 m,透射杆长1 m,子弹长300 mm,冲击压力为1 MPa。使用TDS⁃3014C数字示波器(最高采样频率为1 GHz)记录霍普金森压杆中输入、输出杆上的入射波、透射波及反射波。为减小套筒内壁的摩擦,装入试件前在套筒内壁喷一层脱模剂。压制完成后,将套筒拿到MTS上面对压坯进行脱模。
3 模拟过程及参数选择
使用离散元计算软件PFC3D建立铝粉单向冲击压制的三维离散元模型。PFC软件生成大量颗粒的方式有两种:ball generate(不容许生成的颗粒间发生重叠)和ball distribute(容许生成的颗粒间发生重叠)。为了更接近实际情况下金属颗粒的随机分布情况,本次模拟选择distribute颗粒生成方式,令颗粒间分布着大小不等的作用力,经过适当的循环计算,颗粒间的作用力被均匀分布在各颗粒之间。去除上方墙壁后,受颗粒间的作用力和重力的共同作用,颗粒会在小范围内发生位移,因此颗粒间产生了不均匀分布的缝隙,并且位于模型表层的颗粒分布凹凸不平。这样的模型更接近实际情况。
为了便于模型尺寸参数的设定,本次模拟建立半径为5 mm、高5 mm的圆柱形空间,内部填充直径为0.15 mm的17 680个圆形颗粒(图3),压板以10 m/s的速度沿Z轴向下运动。本次模拟步长设置为10-8s,压板下行行时间25×10-6s,加载前,颗粒重排用时1 000步,加载完成后运算时间忽略不计,总共进行计算3 500步。模拟主要参数如表2所示。
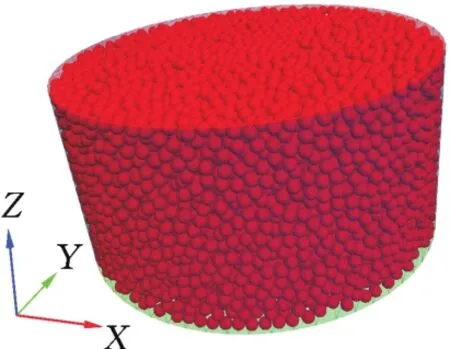
图3 离散元模型图Fig.3 The 3D discrete element model

表2 模拟的主要参数Tab.2 Main parameters of the simulation
4 模拟结果及实验对比
图4所示为在铝粉冲击压制的模拟中采集到的底板中投射波的波形,该图与分离式Hopkin⁃son杆撞击试验中采集的透射波波形图(图5)基本一致。由图4可以看出,在加载过程中,曲线呈锯齿状上升。不同于连续体材料,粉末材料为多孔型离散性排列,颗粒间存在着一定的空间。在高速率的加载情况下,颗粒间通过高频率的撞击传递扰动,因此在透射波的上升过程中会看到明显的振动,加载前期的振动幅度较大,会出现局部卸载,随着粉末的压实,振动情况逐渐减弱。
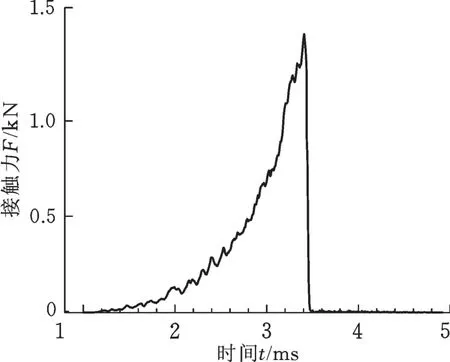
图4 透射波波形的模拟结果Fig.4 Transmission waveform of simulation
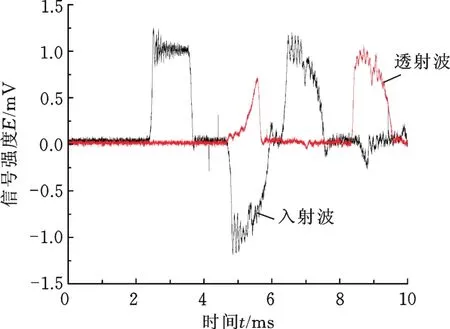
图5 透射波波形的实验结果Fig.5 Transmission waveform of experiment
5 颗粒运动分析
选取位于模型中部、厚0.3 mm(即取两个颗粒直径长度。由于模型中的颗为随机排列,选取一个颗粒直径厚度时,区间内颗粒过少)的垂直横截区域,分析区间内颗粒的速度矢量分布及变化规律,如图6所示。1 000时步时,所有颗粒只受到重力作用,颗粒默认速度矢量方向为垂直方向。加载到1 100时步时,上层颗粒受到冲击,由于颗粒间仍存在较大空隙,因此颗粒相互间会发生剧烈的碰撞,此时上层颗粒的速度方向分布较为混乱,而位于底层的颗粒未受到扰动,速度方向仍为垂直向下。

图6 不同时步时颗粒速度的分布规律Fig.6 Distribution of particle velocity at different time steps
加载到1 500时步时,区域内颗粒已全部受到扰动,颗粒速度方向的分布较为混乱,但可以看出,颗粒之间已初步形成剪切带。当加载到2 000时步时,从速度方向分布图中已经可以看到明显的M型剪切带。模型上部靠近模壁的颗粒会向模壁移动;模型底层的颗粒受到上层颗粒的挤压和底板的阻挡,向四周扩散。2 500时步时,颗粒间的接触更加紧密,速度矢量的分布更加规律。在整个压制过程中,可以看到压坯中颗粒速度存在分布梯度。
从侧面对上述区域内颗粒的速度矢量进行观察分析,如图7所示。第1 000时步时,区域内颗粒未受到冲击,颗粒速度方向默认向下。1 100时步时,颗粒已受到撞击,上层颗粒发生横向移动,而下层颗粒并未受到扰动。随着压制的进行,下层颗粒逐步受到扰动,速度方向为横向,而上层颗粒的速度方向正逐步向下偏转,如图7中1 500、2 000时步时所示。2 500时步时,颗粒间的接触更加紧密,上部颗粒的速度矢量方向变得更加规律,垂直向下。而下部颗粒,由于受到底板的阻挡,速度仍保持横向。
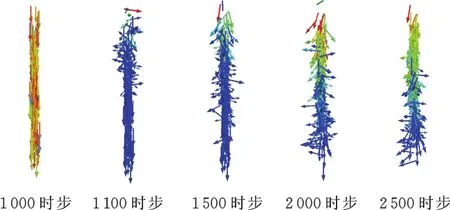
图7 不同时步时颗粒速度的侧面分布Fig.7 Side distribution of particle velocity at different time steps
6 结论
(1)粉末中颗粒的速度分布形状为不规则的弧形,且存在分布梯度。压制过程中可以看到明显的剪切带。
(2)颗粒刚受到冲击时,其移动方向多为横向,随着颗粒速度的增加,颗粒的运动方向会逐渐向下偏移,最终接近于垂直状态。压坯上部的颗粒以纵向移动为主,而下部颗粒多为横向移动,因此导致了压制过程中剪切带的形成。
