汽车三级分段变刚度双质量飞轮非线性振动研究

2018-11-09曾礼平陈齐平袁星星周聪辉黄娟林

中国机械工程 2018年20期

曾礼平陈齐平袁星星肖强周聪辉黄娟林

1.华东交通大学机电与车辆工程学院，南昌，330013

2.广汽丰田汽车有限公司，广州，511455

0 引言

双质量飞轮（dual mass flywheel，DMF）能有效减小汽车传动系中发动机输入的扭转振动［1⁃3］，具有比从动盘式扭振减振器更好的减振效果。各国学者对DMF展开如下研究：①减振弹簧的设计；②系统扭转振动模型的建立和减振性能的分析；③对DMF各项指标的试验分析以及对应试验装置的研制等。吕振华等［4⁃5］、李以农等［6］针对DMF减振弹簧的设计及其参数选择，对汽车传动系统扭转振动的影响进行了研究；KIM等［7］建立了用于分析DMF性能的弹性元件离散化模型，该模型主要包括质量、弹簧及采用模拟非线性摩擦Stribeck作用的分析模型；李光辉等［8］根据汽车传动系统扭转振动的固有频率特性，提出了DMF参数设计方法；WALTER等［9］建立了传动系统中DMF的状态空间方程，提出了实时精确估计发动机转矩的方法；KANG 等［2］、吴飞等［10］建立了DMF工作过程中的角位移和搭载DMF的传动系统扭转测试系统。

LuK公司的分段变刚度DMF的扭转刚度随扭转角的不同而不同，具有明显的非线性。发动机转速不同时，DMF利用刚度变化，将汽车传动系统的共振予以隔离，并满足匹配大功率发动机高转矩的要求［11］。在对搭载DMF的汽车动力传动系统振动特性的理论研究方面，考虑到汽车传动系统和非线性研究的复杂性，一般将系统简化为线性系统进行研究，如刘圣田［12］分析了DMF对汽车怠速振动与噪声控制的影响，建立了怠速状态下发动机的多自由度扭振系统计算分析模型。或只针对DMF结构本身的非线性特征展开研究，如史文库等［13］分析了多级刚度DMF的多级非线性特征，并提出了多级非线性DMF设计过程中各参数的选取原则；SCHAPER等［14］考虑摩擦、惯性力等非线性因素的影响，建立了DMF结构中的长弧形螺旋弹簧的非线性转矩特性的分析模型。这些研究没有详细分析分段变刚度DMF在传动系统中的非线性振动，包括考虑其中的非线性因素、建模和分析方法，本文考虑三级分段变刚度DMF中的初级飞轮和次级飞轮的相对转动，研究了减振弹簧刚度随扭转角分段变化的非线性因素对汽车动力传动系统振动特性的影响。

1 DMF结构及工作原理

图1所示为搭载DMF的汽车动力传动系统，发动机的曲轴与初级飞轮连接，次级飞轮与离合器连接，DMF随着曲轴一起转动，随后动力和运动经过离合器输入到变速箱，最后经过差速器传递到驱动车轮。

图1 搭载DMF的汽车动力传动系统Fig.1 Schematic diagram of vehicle transmission equipped with DMF

所研究的三级分段变刚度DMF如图2所示。初级飞轮与发动机曲轴连接，次级飞轮与离合器相连，起减振作用的减振弹簧与弹簧座置于初级飞轮凸缘之间，螺栓将拨盘与次级飞轮固定。DMF工作时，初级飞轮凸缘与弹簧座接触，弹簧座随着转动，从而压缩安装在2个弹簧座之间的减振弹簧，拨盘在弹簧作用力下转动，与拨盘通过螺栓连接的次级飞轮随之转动。

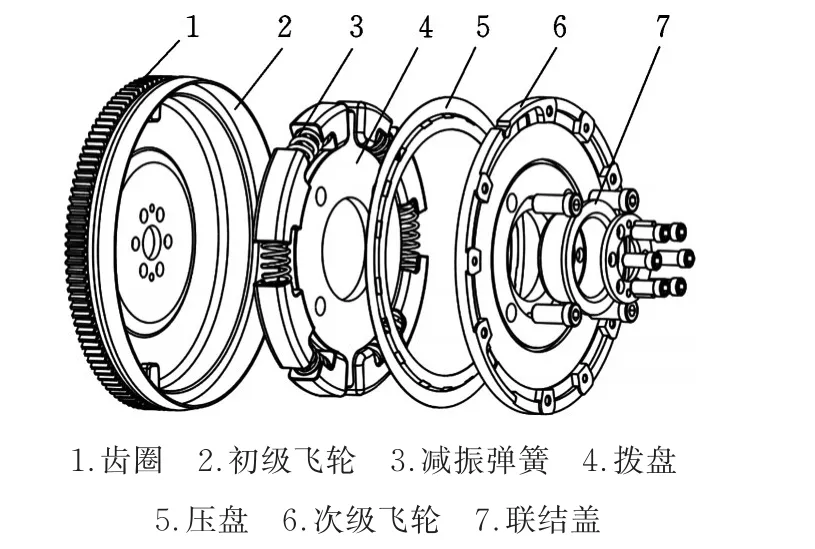
图2DMF结构示意图Fig.2 Schematic plot of the DMF

图3 a为DMF的拨盘、弹簧座、减振弹簧最初相对位置示意图。DMF工作初始阶段，初级飞轮凸缘与弹簧座作用，减振弹簧开始被压缩，在弹簧座相互接触之前，全部减振弹簧串联，此时DMF的扭转刚度为第一级刚度k1，如图3b所示。扭转角增大即转过一定角度后，有4对弹簧座接触，相互接触的2个弹簧座之间的减振弹簧不起传递转矩的作用，此时DMF的扭转刚度为第二级刚度k2，如图3c所示。扭转角转过的角度继续增大，有4对弹簧座相互接触时，只有2个减振弹簧可继续被压缩，这时的DMF扭转刚度为第三级刚度k3，如图3d所示。上述过程对应于如图4所示的DMF转矩及刚度变化。

图3 DMF各级刚度状态示意图Fig.3 Different stage stiffness schematic diagram of the DMF

图4 DMF转矩及刚度特性Fig.4 Torque and stiffness characteristics of DMF

2 汽车传动系统扭振模型

根据图1所示的汽车传动系统，建立对应的系统扭振分析模型，如图5所示，发动机曲轴到初级飞轮的转动惯量用J1表示，次级飞轮和离合器的转动惯量为J2，变速器、差速器等传动系统部件和车轮的等效转动惯量用J3表示。与J1和J2相比，J3是非常大的，并且本文主要考虑DMF自身结构参数的影响，因此对系统进行振动分析时，将J3看成是无穷大［15］。θA和 θB分别为转动惯量J1和转动惯量J2的转角，初级飞轮与次级飞轮之间存在的变刚度所产生的非线性作用力用F（θA，θB）表示，车辆受到地面作用的刚度与阻尼为k、c，T为发动机端输入的转矩。

图5 简化后的汽车传动系扭转振动分析模型Fig.5 Simplified torsional vibration analysis model of vehicle transmission

简化后系统扭振微分方程为

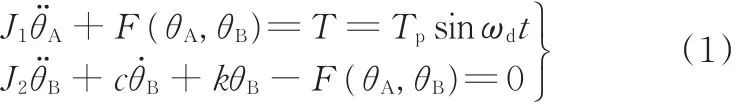
式中，Tp为转矩变化幅值；ωd为激振频率；t为时间。

根据DMF的转矩及刚度特性（图4），用函数表示DMF减振弹簧在不同扭转角范围所产生的非线性作用力：

式中，θ为DMF的扭转角，θ=θA-θB。

3 非线性振动数值求解

3.1 非线性频率特性近似解析解

采用平均法［16］求解式（1），令

则式（2）变为F(θ)=k1θ+g(θ)，将此式代入式（1）得

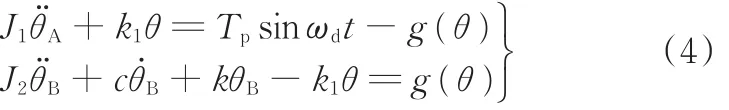
式（4）简化得到

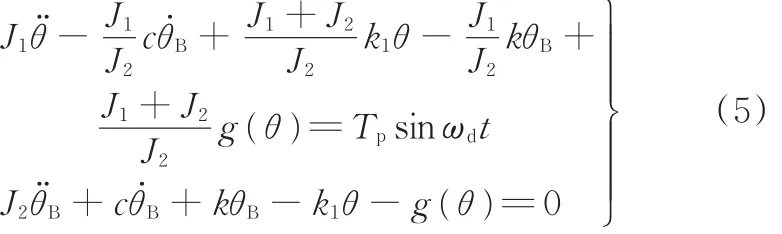
引入小参数ε，将式（5）变换成通用线性振动方程形式：

由式（6）对应的典则方程，推导其派生方程所对应的固有频率计算式：

在代入参数分析计算过程中发现传动系统的1阶共振响应振幅比2阶共振响应振幅大得多，因此，本文只对系统的1阶共振区域的频率特性进行分析。推导得到系统的1阶共振区域振动幅值A1与发动机端输入的外界激励频率ωd的关系：

式中，fe为等效线性固有频率［16］。

由式（8）可知，1阶共振曲线的幅频函数ωd关于fe对称，并且有

3.2 Runge-Kutta数值积分方法

对机械结构的非线性振动研究中，可采用数值方法进行计算，对系统响应的时间变化规律、频率谱特性、相轨迹曲线以及庞加莱截面上的点集分布等方面进行分析，以此判断系统非线性特征［17］。

Runge⁃Kutta数值积分方法常用于微分方程的求解，源于泰勒级数方法，在每个插值点用泰勒级数展开，其中，4阶Runge⁃Kutta法是最常用的一种方法，设y为x的隐函数，且

将区间[a,b]分成i等分，步长h=(b-a)/i，利用已知的 h、xi、yi，计算 k1、k2、k3、k4、yi+1，其截断误差为O(h5)，最后得到y关于x函数的数值解：

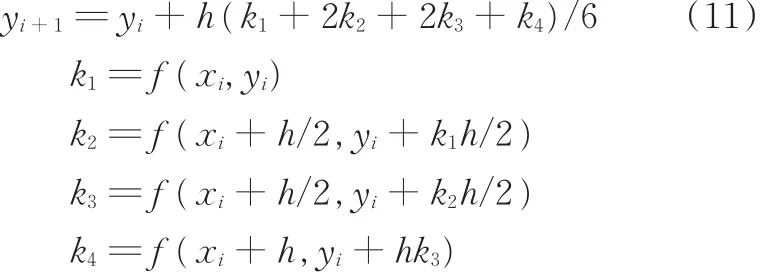
为分析系统强迫振动响应，采用4阶Runge⁃Kutta数值方法，编制算法程序求解式（1）。

4 实例计算与分析

对与某款2.0 L发动机匹配的DMF进行分析，该 DMF 具体参数为 k1=4 N ·m/（°），k2=10 N ·m/（°），k3=24 N ·m/（°），θ1=12°，θ2=35°。图5所示的整车动力传动系统模型中，J1=0.15 kg·m2，J2=0.055 kg·m2，c=0.63 N·m·s/rad，k=2 950 N ·m/（°），通过平均法和 4阶 Runge⁃Kutta数值计算方法编程计算分析，得到系统非线性振动频率特性和强迫振动响应。

4.1 非线性幅频特性

DMF刚度随扭转角变化不是固定值，在特定角度（θ1=12°，θ2=35°）发生跳跃，则搭载DMF的汽车传统系统刚度在对应角度同样发生明显变化，这使搭载DMF的汽车动力传动系统频响曲线存在跳跃现象，具有多值性，如图6所示。

图6 扭转角θ的幅频特性Fig.6 Amplitude-frequency characteristics of angle θ

由于fe是扭转角振幅的非线性函数，而转矩变化又是振幅的非线性函数（式（8）），当扭转角θ变化的幅值大于θ1（DMF的k1变化到k2位置）后，fe的曲线向右侧弯曲，这与幅值小于θ1时fe的曲线为直线完全不同。同样，幅频特性曲线随发动机转矩频率变化也向右侧弯曲。当激励频率逐渐增大即由小到大进行扫频，DMF扭转角振动的幅值也从A点→B点→C点越来越大，随后幅值连续变化到D点位置，若继续增大外界激励频率，扭转角幅值从D点阶跃变化到E点，并沿曲线的右下半分支移动。若激励频率扫频路径为由大到小，扭转角变化的幅值从E点增大到I点（θ2，DMF的k2变化到k3位置），此时若再减小发动机激励频率，扭转角幅值则从I处阶跃变化至C点位置，随后沿幅频曲线减小从B至A点方向连续变化。

4.2 非线性强迫振动响应

由式（7）可计算得到系统的1阶固有频率ωn1=37.64 rad/s，在系统1阶共振频率的附近区域分别取40 rad/s（发动机转速382 r/min）、60 rad/s（发动机转速573 r/min）、80 rad/s（发动机转速764 r/min）、100 rad/s（发动机转速955 r/min）、120 rad/s（发动机转速1 146 r/min）和160 rad/s（发动机转速1 528 r/min）为激励频率，振幅Tp=120 N·m，初级和次级飞轮的初始转角和角位移都为零作为初始条件，对系统强迫振动响应进行数值仿真分析。

（1）外界激励频率（转矩变化频率）ωd=40 rad/s时，DMF的初级和次级飞轮的转角、角速度随时间变化过程如图7所示，图8所示为DMF扭转角θ的时间历程、频谱、相图及庞加莱映射。当发动机端输入的转矩随时间为简谐变化，初级飞轮和次级飞轮均做不规则的旋转运动，次级飞轮角位移和角速度的变化趋势与初级飞轮接近，但振动幅值明显减小，分别由原来的最大值63.6°和54.7 rad/s降低到15.1°和20.2 rad/s，证明了DMF的优良减振效果。

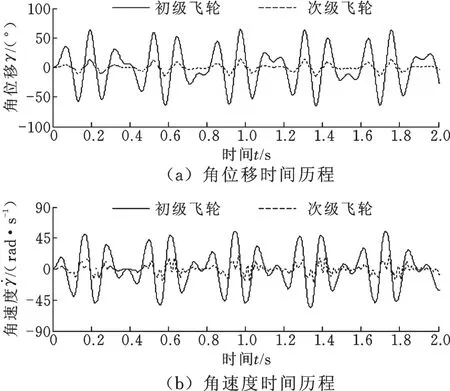
图7 飞轮的角位移、角速度（ωd=40 rad/s）Fig.7 Rotation angles and angular velocities of flywheel（ωd=40 rad/s）

图8 扭转角θ的时间历程、频谱、相图及庞加莱映射截面（ωd=40 rad/s）Fig.8 Time history，frequency spectrum，phase diagram and Poincaré map of angle θ（ωd=40 rad/s）

由图8a所示的扭转角θ不规则运动经过傅里叶变换后得到的频谱如图8b所示，系统响应包含多项幅值和频率均不同的简谐振动：①稳态强迫振动（幅值为26.56°，频率40.21 rad/s≈ωd）；②亚谐稳态强迫振动（幅值为4.07°，频率23.25 rad/s≈ωd/2）；③超谐自由振动（幅值为 1.72°，频率72.88 rad/s≈2ωn1）。另外，DMF扭转角叠加并向外扩散的近似椭圆形的相轨迹（图8c）和其庞加莱截面（图8d）上的点集存在不变环面吸引子，可构成封闭的环形，推断扭转角θ随时间的变化为准周期运动。

（2）ωd=60rad/s时，图9a所示为DMF扭转角θ的时间历程，通过傅里叶变换得到对应的频谱如图9b所示，系统的总响应为：①稳态强迫振动,幅值为 38.47°，频率 60.32 rad/s≈ωd；②幅值为30.87°，频率 67.86 rad/s；③幅值为 11.7°，频率为52.15 rad/s。另外，由DMF扭转角的叠加并向外扩散近似椭圆相轨迹（图9c）和其不可构成封闭的环形的庞加莱截面（图9d）上的点集，可判断扭转角θ随时间变化呈混沌运动状态。

（3）ωd=80 rad/s时，图10a所示为DMF扭转角θ时间历程，经过傅里叶变换得到图10b所示的频谱，系统的总响应为：①亚谐稳态强迫振动（振幅为8.417°，频率43.35 rad/s≈ωd/2）；②稳态强迫振动（振幅为7.853°，频率79.8 rad/s≈ωd）。DMF扭转角θ相轨迹是叠加并向外扩散的近似圆形封闭曲线（图10c），其庞加莱截面上的点集不能构成封闭的环形（图10d），结合频谱和相图可知，DMF扭转角θ处于混沌状态。

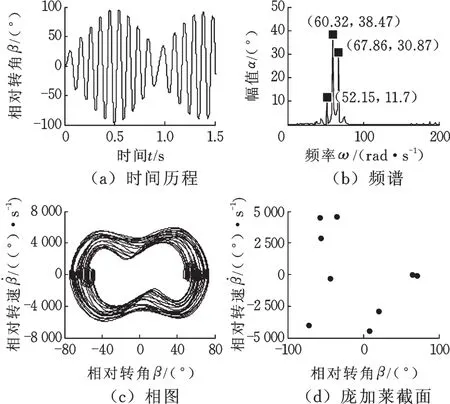
图9 扭转角θ的时间历程、频谱、相图及庞加莱映射截面（ωd=60 rad/s）Fig.9 Time history，frequency spectrum，phase diagram and Poincaré map of angle θ（ωd=60 rad/s）

图10 扭转角θ的时间历程、频谱、相图及庞加莱映射截面（ωd=80 rad/s）Fig.10 Time history，frequency spectrum，phase diagram and Poincaré map of relative angle θ（ωd=80 rad/s）

（4）ωd=100 rad/s时，图11a所示为DMF扭转角θ的时间历程，通过傅里叶变换得到对应的频谱，如图11b所示，系统的总响应主要包括：①亚谐自由振动（幅值0.531°，频率19.48 rad/s≈ωn1/2）；②自由振动（幅值6.568°，频率39.58 rad/s≈ωn1）；③稳态强迫振动（幅值4.76°，频率99.9 rad/s≈ωd）。DMF扭转角的相图为向外扩散的近似椭圆（图11c），其庞加莱截面上的点集不可构成封闭的环形（图11d），可判断DMF扭转角θ随时间变化处于混沌运动状态。

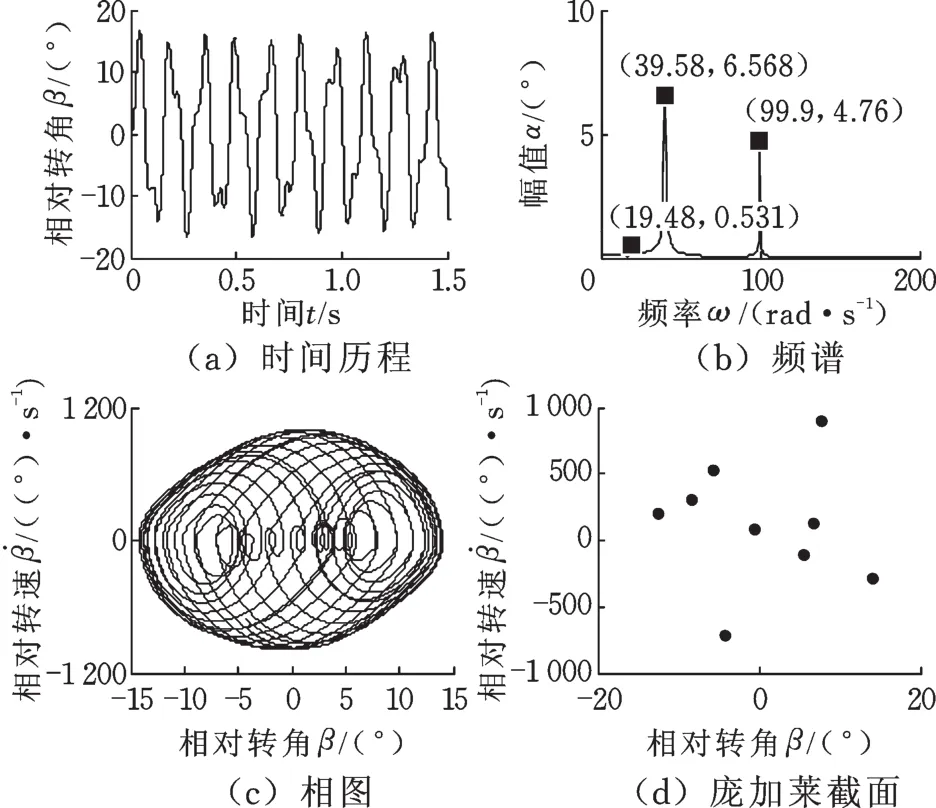
图11 扭转角θ的时间历程、频谱、相图及庞加莱映射截面（ωd=100 rad/s）Fig.11 Time history，frequency spectrum，phase diagram and Poincaré map of angle θ（ωd=100 rad/s）

（5）ωd=120 rad/s时，图12a所示为DMF扭转角θ的时间历程，通过傅里叶变换得到对应的频谱如图12b所示，系统的总响应主要包括：自由振动（频率38.33 rad/s≈ωn1）和稳态强迫振动（频率120 rad/s≈ωd），其中自由振动项的幅值最大。相轨迹为叠加并向外扩散的近似椭圆曲线（图12c），其庞加莱截面上的点集可构成封闭的环形（图12d）。因此，可判断DMF扭转角θ随时间为准周期的变化。

图12 扭转角θ的时间历程、频谱、相图及庞加莱映射截面（ωd=120 rad/s）Fig.12 Time history，frequency spectrum，phase diagram and Poincaré map of angle θ（ωd=120 rad/s）

（6）ωd=160 rad/s时，将图13a所示的不规则变化的DMF扭转角通过傅里叶变换得到图13b所示的频谱，系统的总响应为自由振动（频率37.7 rad/s≈ωn1）和稳态强迫振动（频率160.2 rad/s≈ωd）两项叠加。转角与转速的关系曲线为向外扩散的近似椭圆（图13c），其庞加莱截面上的点集可构成封闭的环形（图13d），因此DMF扭转角θ随时间变化为准周期的。