基于Hansbo渗流的圆球土样Biot固结分析

刘忠玉， 夏洋洋， 朱新牧， 张家超， 郑占垒

(郑州大学 土木工程学院 河南 郑州 450001)

0 引言

在二维或三维固结初期，土体内部的孔压可能不降反升，该现象首先由Mandel在1953年发现，后来Cryer[1]在研究土球受均布压力径向向外排水时也发现此现象，故而称为Mandel-Cryer效应.这一效应并不能用Terzaghi一维或拟多维固结理论解释，而Biot从较严格的固结机理出发推导出的多维固结理论却能很好地解释这一效应，因此，学者们对此展开了大量研究.文献[2]通过试验再次证实了Mandel-Cryer效应，文献[3-6]通过多种方法求解了圆球土样的Biot固结方程，并对Mandel-Cryer效应的影响因素进行了分析，研究结果表明，减小泊松比、渗透系数、杨氏模量等参数或远离排水边界都会延迟Mandel-Cryer效应.但是，这些学者对Biot固结理论的研究都基于Darcy渗流，鲜有学者在研究Biot固结理论时考虑渗流的非线性.早在1925年，Terzaghi就指出大塑性黏性土中的渗流可能偏离Darcy定律.文献[7-12]的渗透试验证实了这一论断，并分别提出不同形式的非Darcy渗流数学拟合公式，其中应用较广的当属Hansbo渗流[7].

目前考虑Hansbo渗流对固结性状影响的研究多集中于一维问题，例如文献[13-21]先后引入Hansbo渗流或其简化形式、指数渗流等修正了Terzaghi一维固结理论，成功解释了后者所不能解释的一些试验现象.随着研究的深入，已有学者开始讨论非Darcy渗流对砂井地基固结的影响[22-23]，但在Biot固结理论框架内讨论非Darcy渗流影响的报道还很少.因此，为深入探讨非Darcy渗流对固结过程的影响，引入Hansbo渗流模型代替Darcy定律，基于Biot固结理论重新推导了圆球土样的固结方程，并探讨了Hansbo渗流参数对固结进程的影响.

1 圆球土样Biot固结方程的推导及求解

1.1 控制方程

设半径为a的饱和圆球土样为均质且各向同性的线弹性体，其弹性模量为E，泊松比为μ.假定土颗粒和孔隙水不可压缩，土球内部没有初始孔压，且土样外表面完全透水.现于其外表面沿径向作用均布压力q，这样土样内的渗流和变形都是球对称的.在外荷载作用下，t时刻距球心r处的径向位移为u，体应变为θ，孔压为p.并且规定径向位移u沿半径方向向外为正，反之为负；体应变θ以收缩为正，反之为负；压力q以压为正，以拉为负.则其平衡方程、物理方程和几何方程分别为

(1)

(2)

(3)

式中：G为剪切模量；εr、ετ分别为径向和环向应变；σr、στ分别为径向和环向应力.

联立方程组(1)～(3)，可得用位移和孔压表示的平衡微分方程为

(4)

体应变θ和径向位移u的关系为

(5)

(6)

设t时刻距球心r处的径向水力梯度为i，径向渗流速度为v，且二者之间的关系可以采用Hansbo渗流公式描述为

(7)

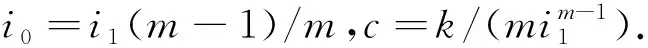
(8)

(9)

考虑渗流连续性，即土骨架的体积变化=孔隙体积变化=流入流出单元体的水量差，则

(10)

将式(8)代入式(10)，可得

(11)

联立式(6)、(11)，可得

(12)

将式(12)代入式(4)，可得

(13)

式中：Cv=kE(1-μ)/[γw(1+μ)(1-2μ)]. 方程组(12)、(13)的边值条件及初始条件分别为

(14)

u(0,t)=0；u(r,0)=0，

(15)

p(0,t)<∞；p(a,t)=0.

模板以1∶50 000地形图为标准底图，增加了乡级行政区域界线、界桩点、界址点、乡镇及以上行政地名表面注记、审核表和制图表等内容。其中对界线、界桩点、界址点及注记的符号与表达方式进行了专题性规定，在附图上作为第一层面的信息展示，并对图例内容进行了相应的扩充与修改。

(16)

为了便于讨论引入下列无量纲化参数：

(17)

则式(12)～(16)可以化为

(18)

(19)

(20)

U(0,T)=0；U(R,0)=0,

(21)

P(0,T)<∞；P(1,T)=0,

(22)

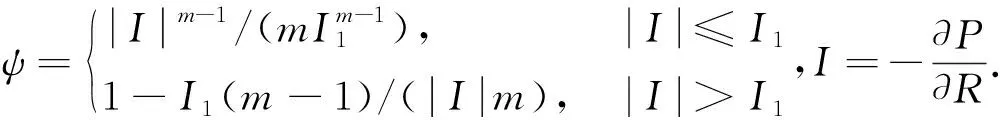
1.2 有限差分法求解

上述微分方程组为变系数抛物型方程，取得其解析解较为困难.因此，拟采用Crank-Nicolson有限差分法求其数值解.即在0≤R≤1范围内以ΔR为步长，将土球由球心沿半径方向离散为N层，而对时间则按步长ΔT进行离散，则式(19)～(21)可离散为

(23)

(24)

(25)

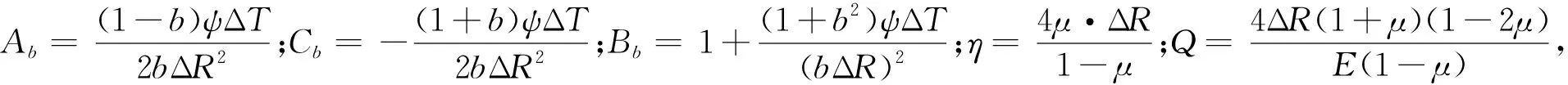
这样由式(23)～(25)可求得位移，然后再利用式(18)和式(22)求孔压，可离散得

(26)

(27)

(28)

假定孔压P在区间[Rb,Rb+1]内为线性分布，则在j时刻的平均固结度为

(29)

2 算法验证

用Matlab软件编制程序，为了验证本文算法及所编程序的正确性，对m=1.0或I1=0即Darcy渗流时的圆球土样固结过程进行了数值模拟.模拟时，取ΔR=0.01，ΔT=0.000 01，得到的土球外边界处的位移随时间的变化曲线示于图1.Cryer[1]曾给出了其解析解，为便于对比，将Darcy渗流时圆球土样的边界位移也示于图1中.可以看出，本文有限差分解与Cryer的解析解基本一致，表明本文算法及所编程序是有效的.

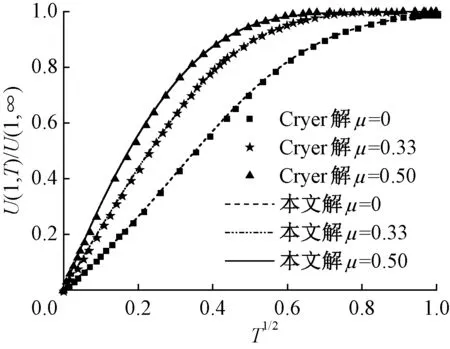
图1 Darcy渗流时圆球土样的边界位移Fig.1 Boundary displacement of the spheroidal soil based on Darcy′ flow

3 参数分析

文献[3-6]讨论了弹性模量和泊松比对土体固结过程的影响，本文仅讨论Hansbo渗流参数的影响，分析中取E=5 MPa，μ=0.35，q=1 MPa.

3.1 Hansbo渗流对孔压的影响

为考察Hansbo渗流对Mandel-Cryer效应的影响，图2给出了m不同时孔压P随时间T的变化曲线.很明显，在加载的初期，孔压都是升高的，达到峰值后再开始消散，即出现了Mandel-Cryer效应.在Darcy渗流条件下，在T=0.017时孔压P达到其峰值1.12.而在Hansbo渗流条件下，当m=1.2、1.5和1.8时，孔压峰值分别为1.21、1.31和1.38，对应的时间分别为0.022、0.027和0.031.因此，Hansbo渗流增强了Mandel-Cryer效应，m越大，该效应越明显，即孔压峰值就越大，且达到峰值所需要的时间也越长.

图3给出了I1不同时孔压P随时间T的变化曲线.I1对Mandel-Cryer效应的影响规律和m值相似，即I1越大，孔压峰值就越大，且达到峰值所需要的时间也越长.

另外，图2和图3还表明，在孔压达到峰值后转入消散的固结中后期，Hansbo渗流将使圆球土样内的孔压消散滞后，并且其参数越大，这种滞后越明显.

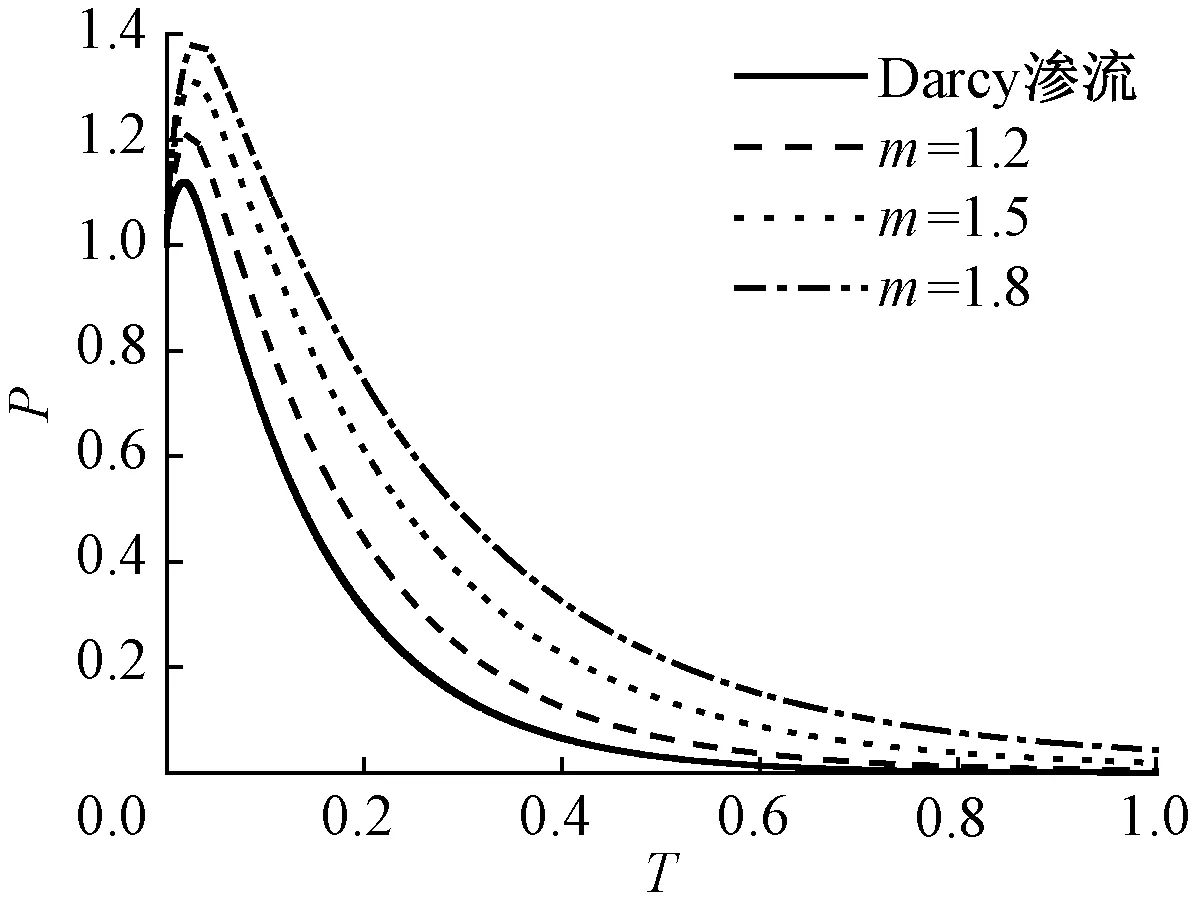
图2 m对孔压的影响(I1=1.0, r=0.5a)Fig.2 Influence of m on pore water pressure (I1=1.0, r=0.5a)

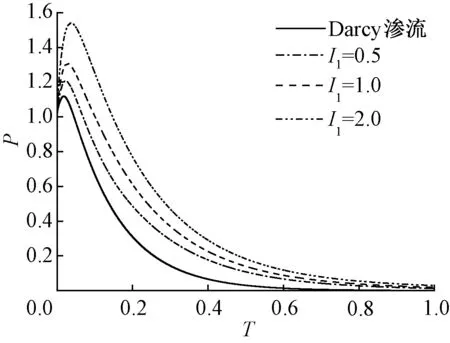
图3 I1对孔压的影响(m=1.5, r=0.5a)Fig.3 Influence of I1 on pore water pressure (m=1.5, r=0.5a)

3.2 Hansbo渗流对固结度的影响

平均固结度Ut反映了圆球土样的固结程度，也就是圆球土样在相应时刻的孔压整体消散程度.为考察Hansbo渗流对平均固结度的影响，图4和图5分别给出了不同m或I1时平均固结度Ut随时间T的变化曲线.很明显，基于Hansbo渗流计算的固结度曲线都在基于Darcy渗流计算的曲线下方，并且Hansbo渗流参数I1或m越大，相应的曲线偏离基于Darcy渗流计算的曲线越远，即固结度Ut随着Hansbo渗流参数m和I1的增大而减小，也就是说圆球土样内孔压的整体消散随Hansbo渗流参数m和I1的增大而减缓，这与文献 [16]中 Hansbo渗流对一维固结影响的结论相似.

3.3 Hansbo渗流对边界位移的影响

记U(1,∞)为圆球土样边界处的最终位移，则U(1,T)/U(1,∞)为边界处T时刻的无量纲位移，类似于一维固结时按变形定义的固结度Us.按照文献[16，18，21]的分析，对于一维弹性饱和地基来说，不论Darcy渗流还是Hansbo渗流，按变形定义的固结度Us和按孔压定义的固结度Ut是一致的，但对于圆球土样却不是这样的.图6和图7分别给出了不同Hansbo渗流参数下U(1,T)/U(1,∞)随时间T的变化曲线.很明显，这些曲线与图4和图5所示的Ut随T的变化曲线尽管趋势一样，但数值相差却很大；尽管Hansbo渗流参数越大，同一时刻的边界位移会越小，但从图6和图7的几条曲线几乎重合来看，其数值相差无几，所以Hansbo渗流对边界位移的影响很小.

图4 m对固结度的影响(I1=1.0)Fig.4 Influence of m on degree of consolidation (I1=1.0)

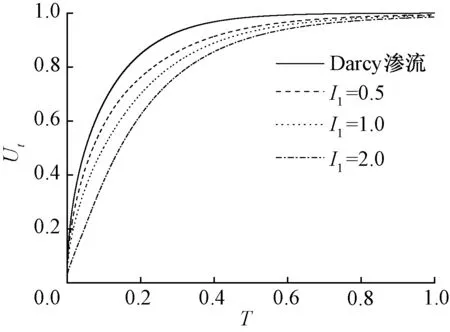
图5 I1对固结度的影响(m=1.5)Fig.5 Influence of I1 on degree of consolidation (m=1.5)

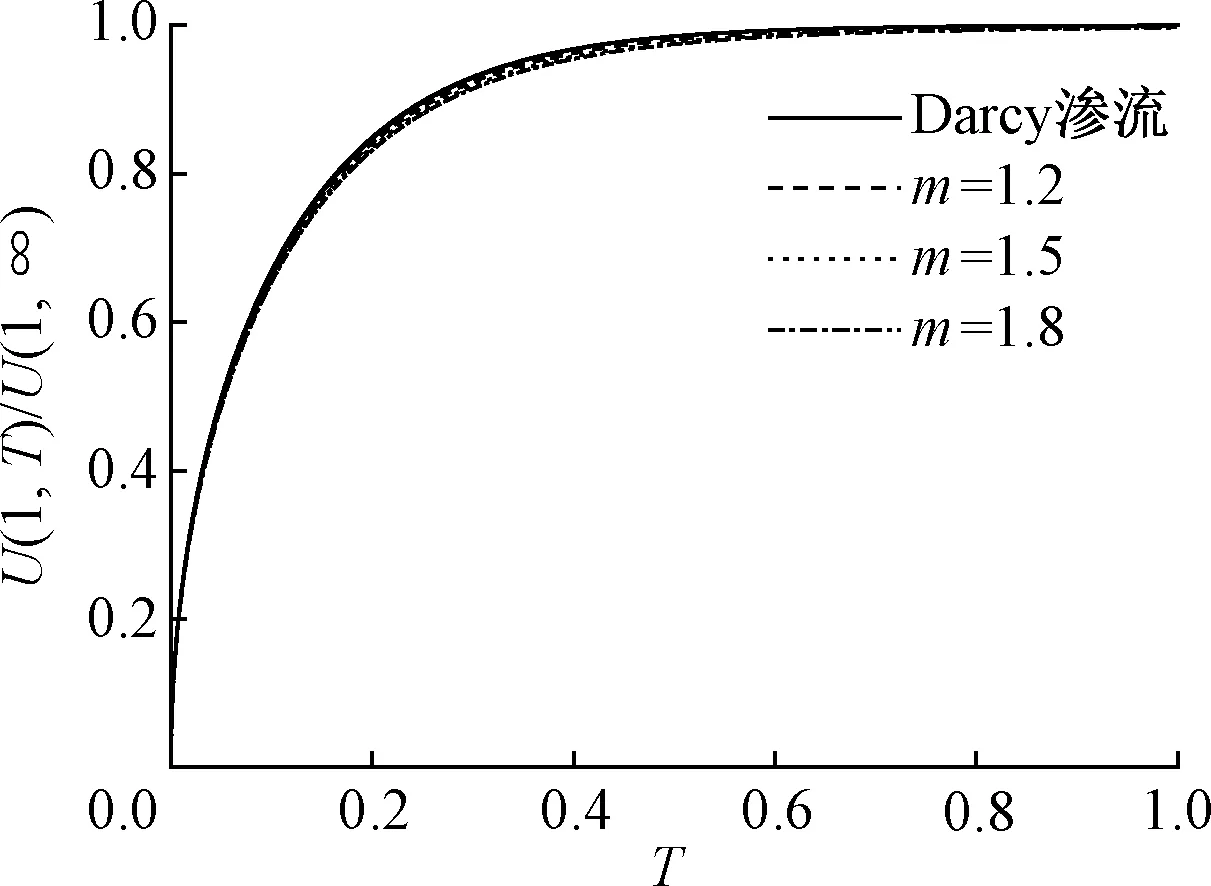
图6 m对边界位移的影响(I1=1.0)Fig.6 Influence of m on boundary displacement (I1=1.0)

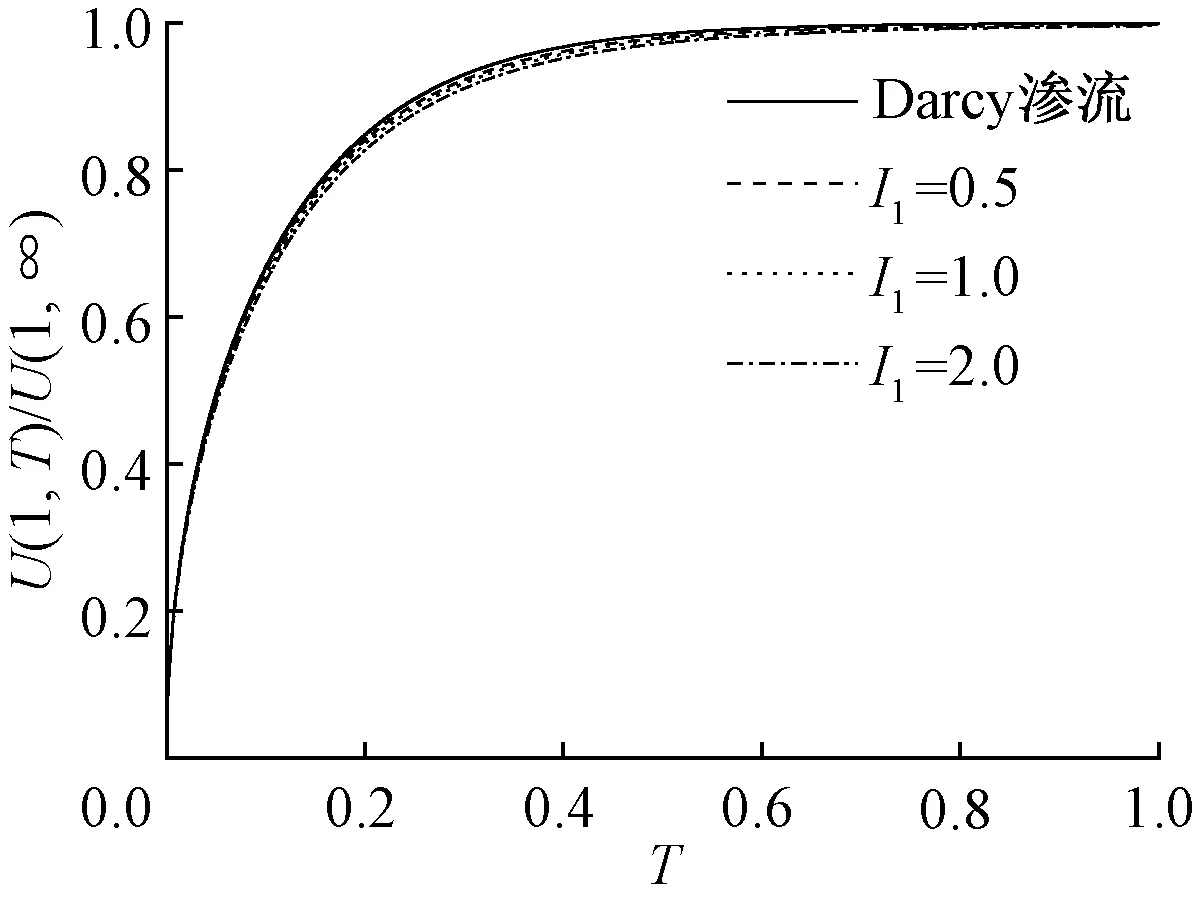
图7 I1对边界位移的影响(m=1.5)Fig.7 Influence of I1 on boundary displacement (m=1.5)

4 结论

基于Hansbo渗流模型推导了圆球土样Biot固结方程，给出了方程的Crank-Nicolson有限差分格式，并用Matlab软件编写了有关程序.计算结果表明：和Darcy渗流相比，在固结初期，Hansbo渗流将增强Mandel-Cryer效应，增大孔隙水压力的峰值，并延长孔隙水压力达到峰值的时间；在固结中后期，Hansbo渗流将使圆球土样内孔压消散明显滞后.随着Hansbo渗流参数的增大，土样平均固结度减小，即土样固结速率减慢，但Hansbo渗流对边界位移的影响很小.