带有Neumann条件的对流扩散方程的两层紧差分格式
2018-11-08盛秀兰吴宏伟
盛秀兰, 魏 贞, 吴宏伟
(1.东南大学 数学学院 江苏 南京 210096; 2.江苏开放大学 通识教育学院 江苏 南京 210036)
0 引言
考虑带有Neumann边界条件的一维常系数对流扩散方程构造高阶差分格式:
ut+αux-βuxx=f(x,t),x∈(a,b),t∈(0,T],
(1)
u(x,0)=φ(x),x∈(a,b),
(2)
ux(a,t)=0;ux(b,t)=0,t∈(0,T],
(3)
其中:α,β为常数,且β>0.
ut+αv-βuxx=f(x,t),x∈(a,b),t∈(0,T],
(4)
vt+αuxx-βvxx=fx(x,t),x∈(a,b),t∈(0,T],
(5)
u(x,0)=φ(x);v(x,0)=φ′(x),x∈(a,b),
(6)
v(a,t)=0;v(b,t)=0,t∈(0,T],
(7)
令v(x,t)=ux(x,t),则方程(1)转化为方程(4),同时对方程(1)关于x求一阶导数为方程(5).方程(4)~(7)为耦合方程,与(1)~(3)式等价.
对流扩散方程是描述黏性流体运动的非线性模型方程,但要得到对流扩散方程的精确解很困难,因此有效的数值算法越来越重要,在常用的差分方法中,由于方程中扩散项的存在,在数值求解过程中经常会出现数值震荡,为此需要构造精度高、稳定性好的数值解法,紧差分格式就是这一类方法.文献[1]给出了二维变对流系数非稳态对流扩散方程的时间方向上加权离散的一类HOC格式.文献[2]给出了二维不稳定对流扩散方程的一种高阶交替方向隐格式,此方法在时间和空间上分别是二阶和四阶的.文献[3-4]研究了对流扩散方程的特征有限差分格式,此方法能够有效地克服数值震荡.文献[5-6]给出了关于Neumann边界条件热方程的高阶差分格式.文献[7-8]通过紧差分格式及高阶ADI格式研究对流扩散问题.文献[9]提出带有Neumann边界条件的非线性反应扩散方程的一种四阶紧算法.文献[10]通过引入新变量,建立了一维非稳态对流扩散方程的高阶有限差分格式,利用Von-Neumann方法分析了差分格式的稳定性,在时间和空间上为二阶和四阶收敛.文献[11-12]利用紧差分格式求解热方程、变系数线性抛物方程及Cahn-Hilliard方程.本文参考文献[13]利用离散能量估计方法证明了差分解在最大模意义下关于时间和空间的二阶收敛性.对带有Dirichlet边界条件的对流扩散方程建立高阶紧差分格式的方法很多,而处理Neumann边界条件方法比较棘手,本文针对一维对流扩散方程建立一种紧差分格式,拟从格式的相容性、截断误差、稳定性、收敛性、以及精度等方面对Neumann边界条件进行研究.
1 记号及引理
取正整数m,n,记空间步长与时间步长分别为h=(b-a)/m,τ=T/n.xi=a+ih,(0≤i≤m),tk=kτ,(0≤k≤n).定义Ωh={xi|0≤i≤m},Ωhτ={(xi,tk)|0≤i≤m,0≤k≤n},称(xi,tk)为节点,并设{vik|0≤i≤m,0≤k≤n}为Ωhτ上的网格函数,引进下列记号:
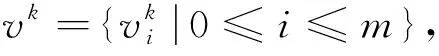

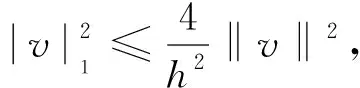
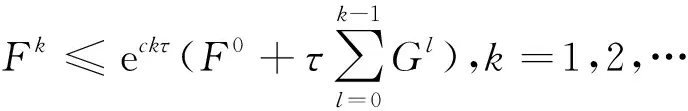
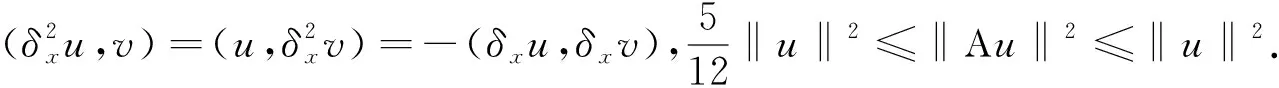
引理5[16]① 若f(x)∈C5[x0,x1],则
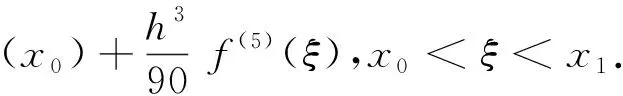
② 若f(x)∈C5[xm,xm-1],则
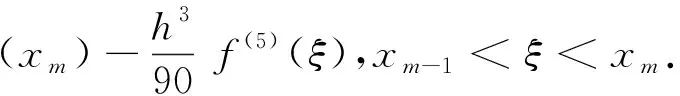
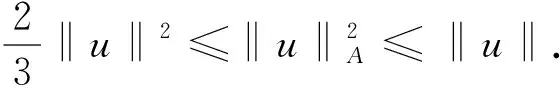
2 差分格式的建立
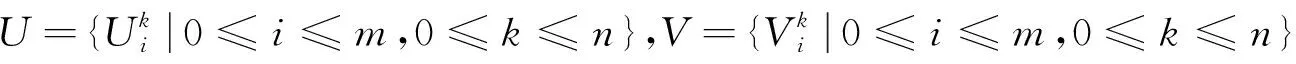
(8)
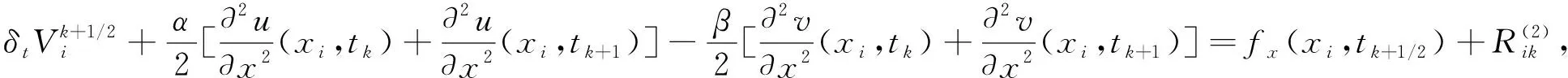
(9)
当0≤i≤m,0≤k≤n-1时,用算子Α分别作用于(8)和(9)两式得
(10)
(11)
当0≤i≤m-1,0≤k≤n-1时,并由引理1将(10)和(11)两式转化为:
(12)
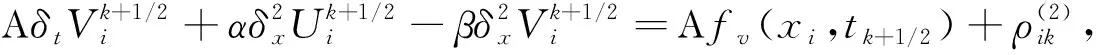
(13)
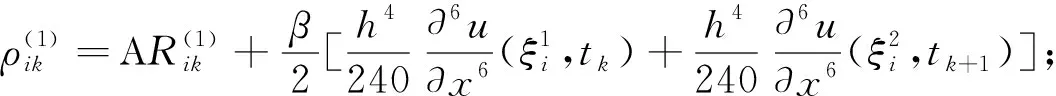
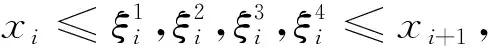
由(10)式知,当i=0,0≤k≤n-1时
(14)
应用引理5将(14)式转化为
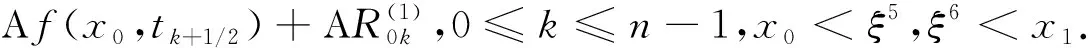
(15)
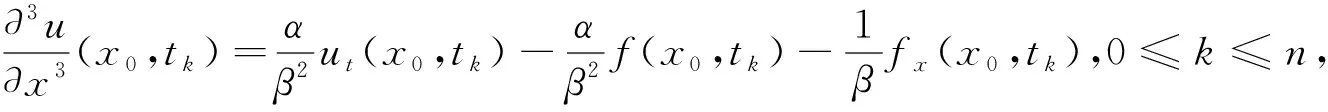
(16)
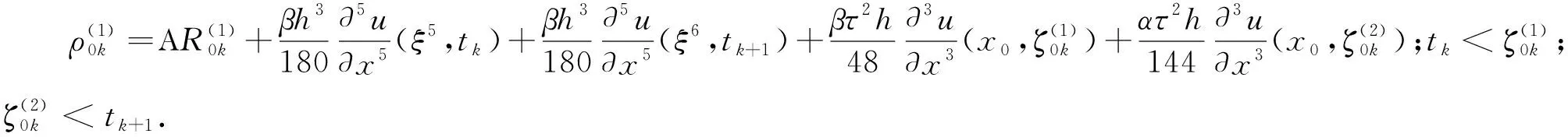
(17)
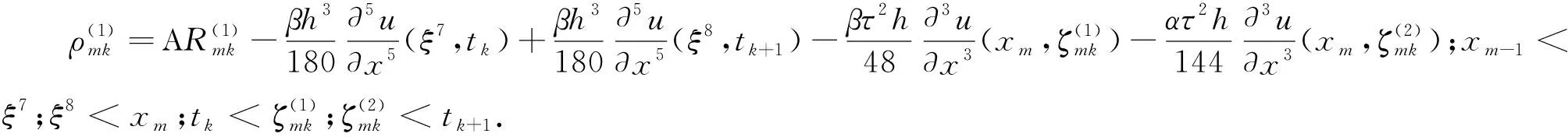
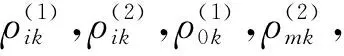
(18)
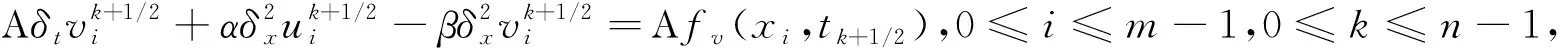
(19)
(20)
(21)
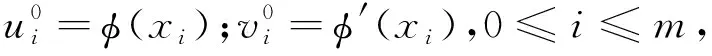
(22)
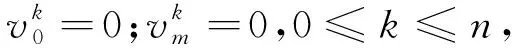
(23)
3 差分格式解的先验估计式
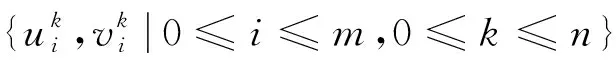
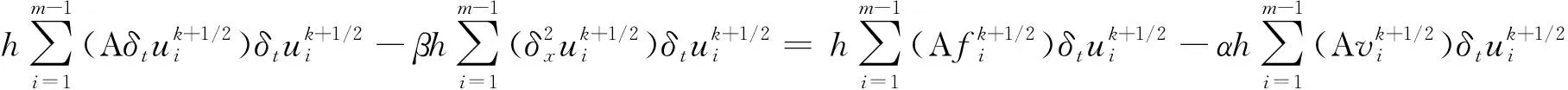
(24)
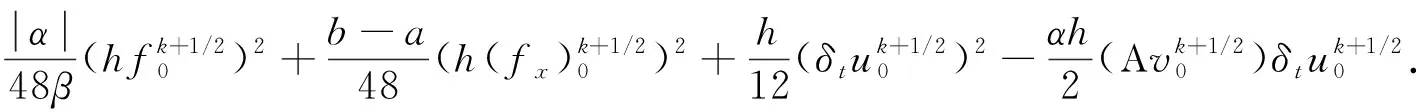
(25)
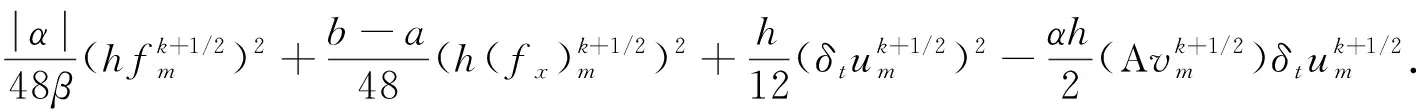
(26)
将(24)~(26)三式相加得
(27)
(28)
(29)
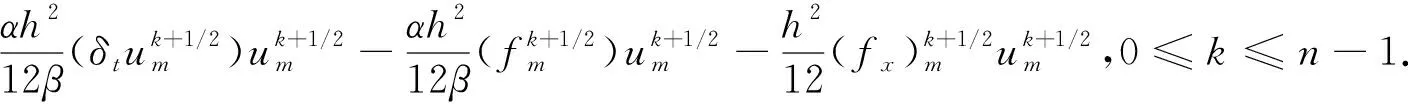
(30)
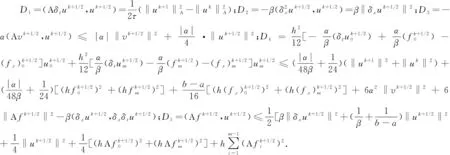
将D1,D2,D3,D4,D5代入D1+D2=D3+D4+D5得
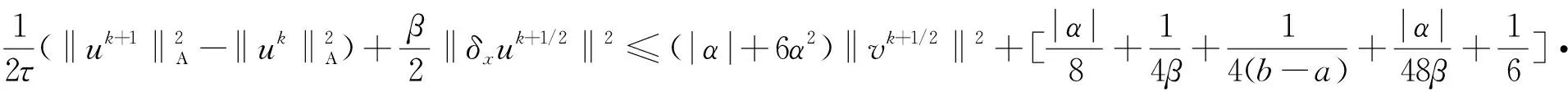
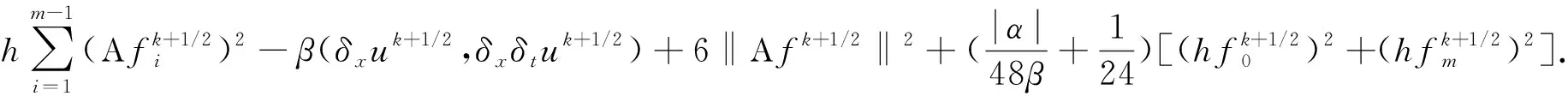
(31)
(32)
(32)式左边第1项、第2项分别为:
(32)式右边第1项、第2项分别为:
其中ε=-β/|α|,将上述4项代入(32)式得
(33)
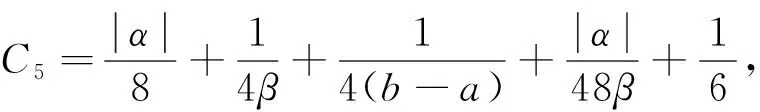
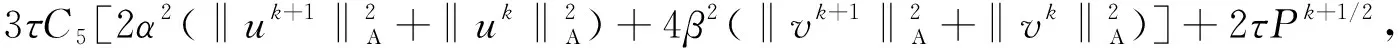
(34)
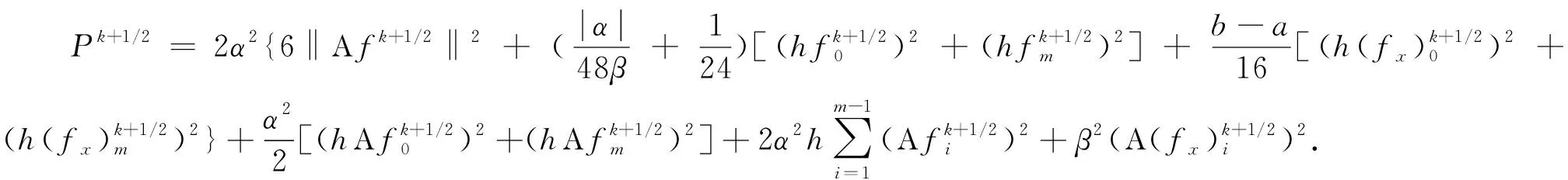
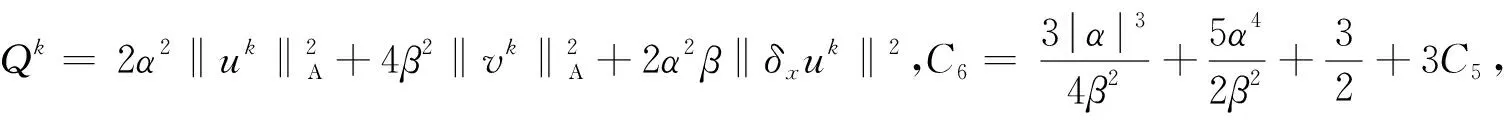
定理2得证.
4 差分格式的唯一性、收敛性和稳定性
1) 唯一性
定理2差分格式(18)~(23)式是唯一可解.
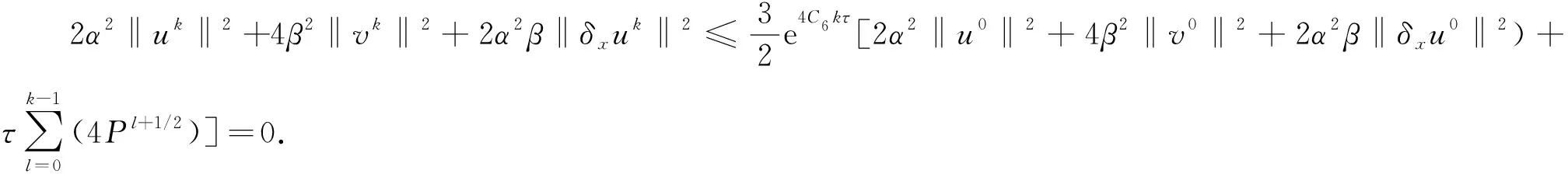
2) 收敛性
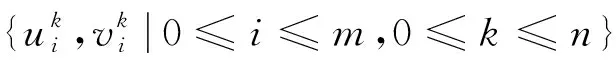
证明将(3)~(7)式与(18)~(23)式分别相减,得到误差方程组:
由定理2知,定理3成立.
3) 稳定性
类似讨论差分格式的收敛性,可以得到差分格式(18)~(23)式关于初值的稳定性.
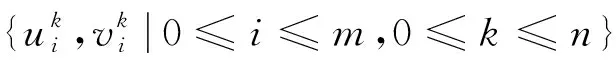
5 数值试验
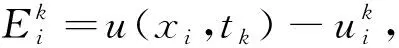
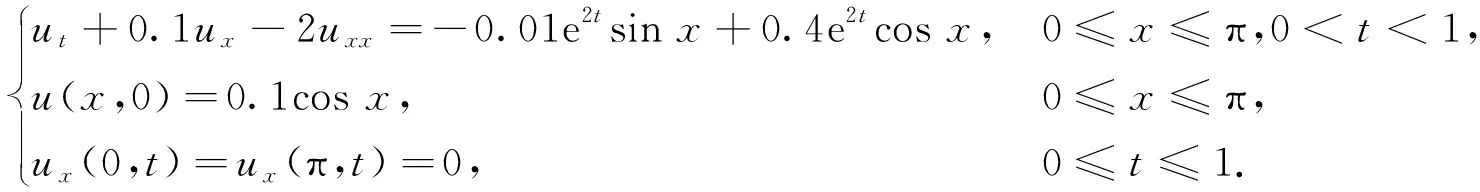
该问题的精确解为u(x,t)=0.1e2 tcosx.

表1 不同步长下的误差和收敛阶数Tab.1 Errors and convergence rate under different steps
