基于GA-SVM的高压输电线路弧垂预测模型

姬 波， 杨文东， 张 驰， 卢红星， 安致嫄

(1.郑州大学 信息工程学院 河南 郑州 450001； 2.国网河南省电力公司信息通信公司通信运行部 河南 郑州 450000)

0 引言

高压输电线路的弧垂是反映线路安全运行的重要参数，也是输电线路在线监测和动态增容重点关注的指标之一[1-2]，当前国内外都非常重视输电线路弧垂的监测研究. 现有弧垂的监测方法主要有：图像技术法[3]，GPS监测法[4]，倾斜角法[5]以及通过导线温度和应力测量弧垂[6-7]等. 但是，除了实时监测弧垂变化外，预知和预警弧垂变化也是一个亟待解决的问题，目前还未见有这方面相关的研究.

SVM是一种基于统计学习理论的机器学习算法，已被广泛应用到现代经济和工业领域中[8]. 文献[9]通过支持向量回归算法建立股票分析模型，对股票价格进行预测分析.文献[10]应用支持向量机算法对混凝土抗压强度进行预测.文献[11]采用支持向量回归算法对山西月度最大电力负荷进行预测.文献[12]进行项目控制预测. 因为线路运行的电压、电流、导线的温度，以及周围环境的温度、风速、湿度等都会造成输电线路弧垂的变化[13]. 本文提出一种基于GA特征自适应赋权的SVM预测高压输电线路弧垂的方法(GA-SVM). 该方法主要分为两个阶段：1) 根据每个属性对弧垂影响的重要程度不同，使用GA自适应对特征赋权，以突出重要属性，抑制次要或冗余属性. 2) 以第一阶段处理过的数据作为SVM的输入，对弧垂进行预测分析. 实证研究表明，本文提出的基于GA-SVM预测高压输电线路弧垂的方法是可行和有效的，并且其预测精度优于Bayes算法、KNN算法、决策树算法和BPNN神经网络算法.

1 背景

1.1 输电线路弧垂

输电线路任一点的弧垂是指该点与悬线两端连线的铅锤距离，通常所说的弧垂是指一个档距导线段的最大弧垂. 输电线路的弧垂是线路设计和安全运行的重要指标，弧垂过小，会导致输电线应力过大，影响输电线路的机械安全；弧垂过大，将导致输电线距离地面太低，会造成对地放电的危险. 因此必须保证弧垂在规定的安全范围内.

1.2 支持向量机

SVM在构造最优分类超平面时，采用迭代训练算法来减小误差函数. SVM分类模型可以描述为一个数学优化问题，所用公式为

(1)

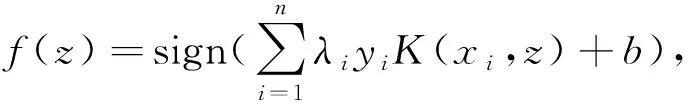
2 基于GA-SVM的高压输电线路弧垂预测模型

2.1 离散化方法

输电线路弧垂是连续属性，但有时候预测弧垂属于哪一个范围比预测弧垂的确切值更有意义. 所以本实验采用等宽离散化方法把弧垂离散化为N个区间.等宽离散化方法是一种典型的无监督离散化方法，是将属性的值域划分为具有相同宽度区间.等宽离散化算法过程如下所示.

输入： 属性A，A的个数为M，离散区间个数为N；

输出： 离散化后的属性为F.

1) 计算A的最大值MAX和最小值MIN.

2) 计算属性A的离散区间宽度W=(MAX-MIN)/N.

3) F=A

4) For i in M do

5) For j in N do

6) If Ai<=MIN +j*W

7) Fi=j

8) Else

9) Continue

10) End

11) End

12) Return F.

2.2 特征变换

2.3 基于GA特征自适应赋权

特征权重可以有效提高模型的精确度[14-15]. 特征权重是对数据的各个特征赋予不同的重要程度，从而达到突出重要特征，抑制次要特征或冗余特征.主要有以下3种方法：1) 单一权重方法赋权；2) 综合权重方法赋权；3) 自适应赋权. 自适应赋权是一种客观的赋权方法，不需要人为干预，能更有效地搜索重要特征，抑制次要特征或冗余特征提高模型精度[16-17]. 本文采用基于GA的特征自适应赋权方法.

GA是一种求解问题高效并行的全局自适应搜索方法[18]，以自然选择和遗传理论为基础，在搜索过程中自动获取和积累有关搜索空间知识，并自适应地控制搜索过程以求得最优解. 利用遗传算法实现特征自动赋权步骤如下.

1) 基因编码. 本文采用表达精确的浮点数编码方法.

2) 种群初始化. 随机生成M个染色体组成一个群体，群体内个体的数量即是群体规模，每个初始个体即表示问题的初始解.

3) 计算个体的适应度. 适应度函数是唯一评价个体好坏的标准. 在GA寻优过程中，一个良好的适应度函数能够指导寻优的方向. 为了保证GA能搜索到最优的特征权值，定义的适应度函数为Fitness=N′/N，其中：N′表示进行特征赋权后，能够正确分类训练实例的个数；N表示用于训练实例的总个数.

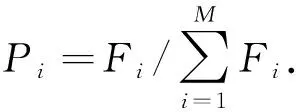
5) 交叉. 交叉是遗传算法中最主要的遗传操作，且是产生新个体的主要方式之一. 本文采用分散交叉法.

6) 变异. 变异是模拟生物进化中的基因突变，它使GA在接近最优解邻域时能够加速向最优解收敛. 本文选用高斯函数作为变异函数.

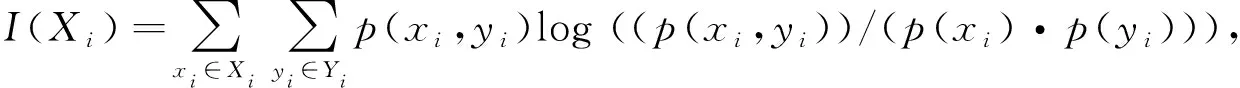
2.4 GA-SVM预测高压输电线路弧垂方法

本文所提出的输电线路弧垂预测模型是一个多阶段的过程：包括数据的特征变换，GA特征自适应赋权，支持向量机预测弧垂，性能评价. GA-SVM预测输电线路弧垂算法过程如下.

输入： 训练数据集Train_set，测试集Test_set；

输出： 弧垂预测值L.

1) 使用标准化特征变换方法处理训练数据集Train_set，得到Train_set1.

2) 使用遗传算法自适应计算Train_set1的特征权重，得到Train_set2.

3) 使用Train_set2作为SVM的输入，训练SVM.

4) 把测试集Test_set输入到训练好的SVM模型中.

5) 得到弧垂预测值L.

3 实验

3.1 实验数据集

实验数据取自郑州市某电力公司，共1 502条记录，每条记录包括6个属性：输电线路温度、环境温度、环境风速、环境湿度、载荷电流、输电线路弧垂. 本实验以前5个属性作为GA-SVM算法的输入属性，输电线路弧垂作为预测属性.

3.2 实验性能评估方法

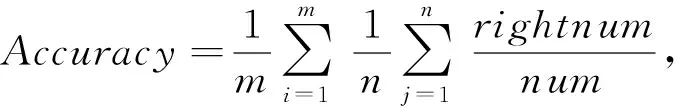
3.3 实验结果

在本实验中，使用台湾大学林智仁教授开发的LIBSVM工具箱进行输电线路弧垂预测. 其中，支持向量机类型选择c-SVC，核函数选择径向基函数，惩罚系数c和内核参数g使用网格搜索算法进行寻优. 网格搜索算法是支持向量机参数寻优常用的一种方法，它将待选取的参数限定在一定的取值范围内，然后将参数按一定的步长分割成一个个网格，同时按次序遍历网格内的所有点，从而获取最优参数组合. 网格搜索算法得到的最优参数组合为：惩罚系数c=2 048，内核参数g=0.007 812 5.

3.3.1不同离散化区间个数的实验结果 表1给出了5种不同等宽离散化区间个数的10次十折实验结果. 从表1可以看出，随着类标属性离散化区间个数的增加，输电线路弧垂的预测准确率逐渐下降. 弧垂离散化为3箱的10次十折平均预测准确率为76.68%，比离散化为7箱的平均预测准确率59.95%高16.73%. 但是较少的区间划分不能充分反应弧垂的变化，而较多的区间划分准确率又太低. 所以综合考虑输电线路弧垂的分布状态，本实验把弧垂等宽离散化分为5个区间.

3.3.2特征变换后的实验结果 表2给出了4种特征变换的10次十折实验结果，包括未进行特征变换的SVM方法，MAX-MIN特征变换的SVM方法，反正切特征变换的SVM方法和标准化特征变换的SVM方法. 从中可以看出：

1) 未进行特征变换的SVM方法10次十折平均正确率是71.38%，比MAX-MIN特征变换和反正切特征变换的SVM方法平均正确率分别高11.91%和13.16%，比标准化特征变换的SVM方法平均正确率75.10%低3.72%. 这说明合理的特征变换能够提高弧垂的预测精度，不当的特征变换则降低预测精度.

2) 标准化特征变换的SVM方法10次十折平均正确率最高，比未进行特征变换的SVM方法提高3.72%，比MAX-MIN特征变换和反正切特征变换的SVM方法分别提高15.63%和16.88%. 这说明本文采用的标准化特征变换方法能够更加准确地描述实验数据特征，从而提升弧垂的预测正确率.

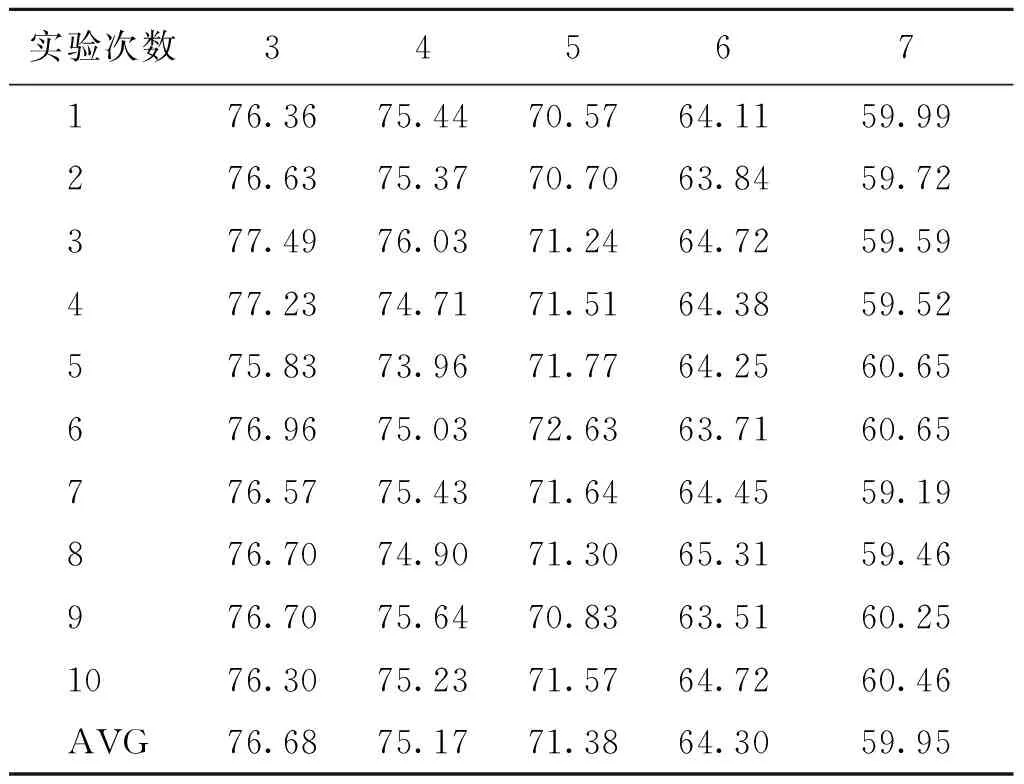
表1 5种不同离散化区间个数的实验结果对比

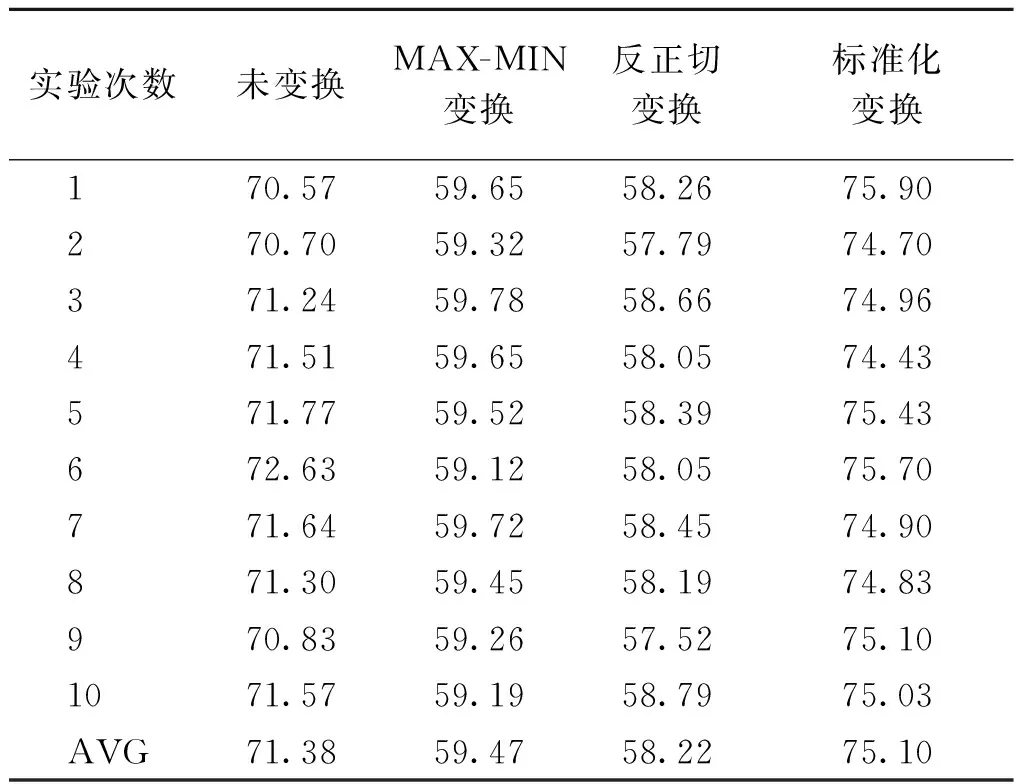
表2 4种不同特征变换方法的实验结果对比

3.3.3特征加权后的实验结果 上述实验说明本文提出的标准化特征变换是最佳的特征变换方法，在此基础上，我们采用特征加权方法对实验数据赋权，以突出重要属性，抑制冗余或次要属性. 表3给出了标准化特征变换并加权后的实验结果. 从表3中可以看出：GA自适应特征赋权方法10次十折实验平均正确率最高，比未加权方法提高2.68%，比熵权重方法提高3.32%，比互信息权重方法提高3.5%. 这说明GA自适应特征赋权方法能够进一步突出重要属性，抑制冗余或次要属性，从而提高SVM预测输电线路弧垂的精度.

为了更详细地分析特征权重对实验结果的影响，在图1和图2中分别给出了10组十折实验的第1组和第2组GA权重、互信息权重和熵权重的正确率曲线. 可以看出：

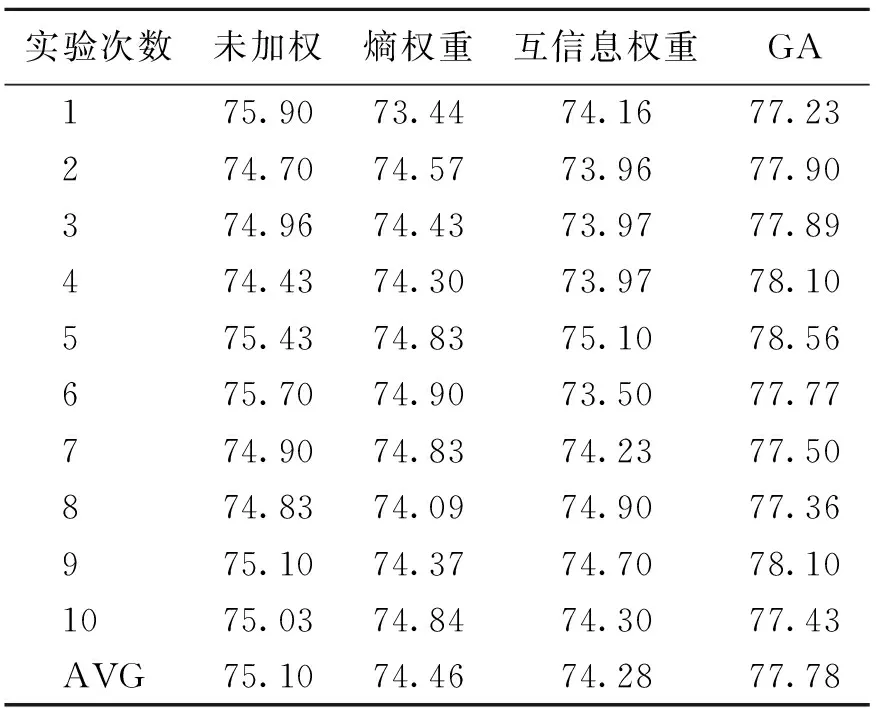
表3 标准化特征变换并加权后的实验结果对比

1) 在第1组的10个数据集上，GA权重在其中的6个数据集上优于互信息权重，在1个数据集上等于互信息权重，在2个数据集上低于互信息权重；GA权重在其中的7个数据集上优于熵权重，在3个数据集上低于熵权重.

2) 在第2组的10个数据集上，GA权重在其中的8个数据集上优于互信息权重，在1个数据集上等于互信息权重，在1个数据集上低于互信息权重；GA权重在其中的9个数据集上优于熵权重，在1个数据集上低于熵权重.

3) GA权重的效果在总体上优于互信息权重和熵权重，更适合用于本实验数据集进行特征赋权，以突出重要属性，抑制冗余或次要属性.

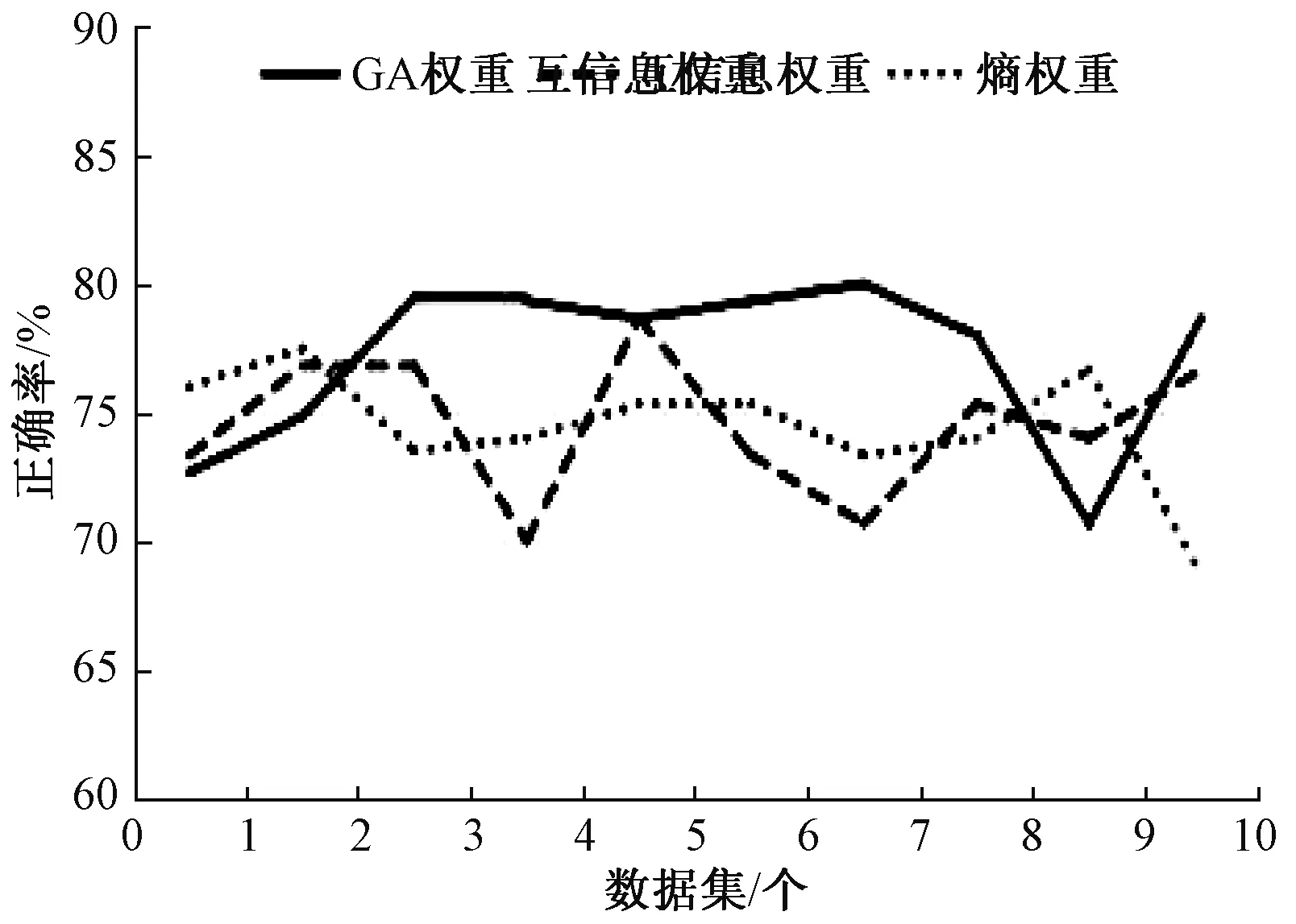
图1 第1组3种特征权重方法正确率曲线对比Fig.1 Correctness curve comparison of three kinds feature weighting methods in the first group

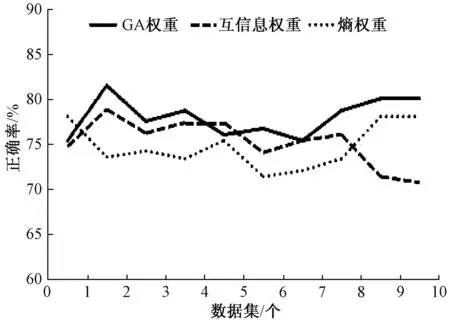
图2 第2组3种特征权重方法正确率曲线对比Fig.2 Correctness curve comparison of three kinds feature weighting methods in the second group

3.3.4与其他机器学习算法实验对比 为了验证本文所提出方法的有效性，图3给出了贝叶斯算法、KNN算法、决策树算法、BPNN神经网络算法和本文提出的GA-SVM方法的10次十折实验的正确率对比柱状图. 贝叶斯算法输入特征离散化采用等宽离散化方法，图中所示Bayes_9表示将每个属性分别离散为9箱后的实验结果. KNN算法的输入属性采用标准化方法变换，图中所示KNN_9表示KNN算法采用9近邻. 图中所示Tree表示决策树采用CART算法. BPNN神经网络采用3层网状结构，5个输入节点，10个隐藏层节点，5个输出节点，激活函数选用logsig和purelin，网络训练函数选用traingdm. 图中所示BPNN_0.3表示神经网络采用0.3作为学习速率训练BPNN模型. 从图3中可以看出，参与比较的5种算法中，本文所提出的GA-SVM算法预测输电线路弧垂的10次十折正确率均是最优，且明显高于其他4种算法.

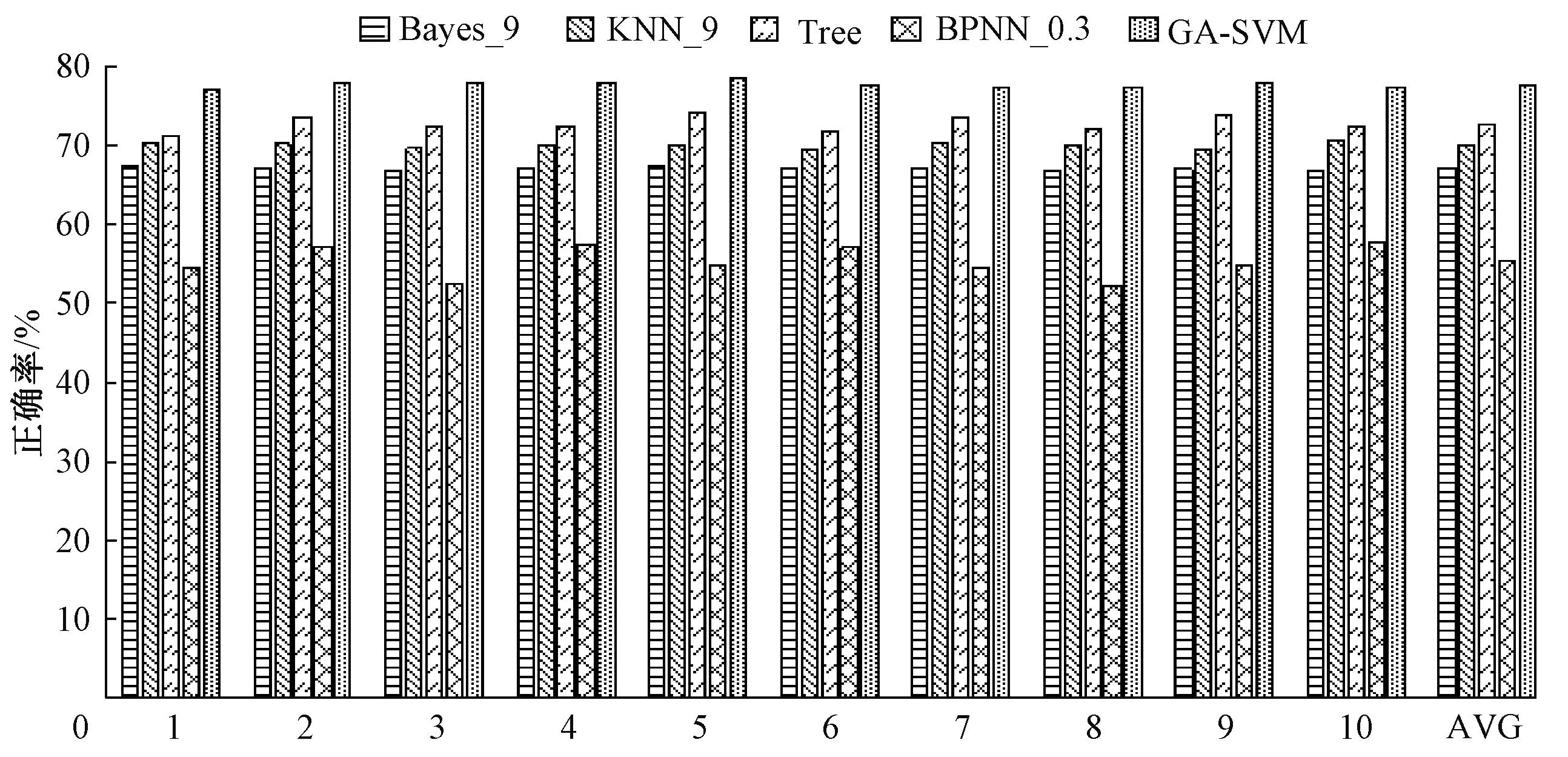
图3 5种算法最优结果对比Fig.3 Five algorithms optimal results comparison

4 结束语

针对在预测高压输电线路弧垂方面，还未见有相关的研究，本文提出一种基于GA特征自适应赋权的SVM预测高压输电线路弧垂方法(GA-SVM). 该方法首先使用GA给实验数据自适应赋权，以突出重要属性，抑制冗余或次要属性，然后再使用SVM预测输电线路弧垂. 实证结果表明，本文提出的GA-SVM预测输电线路弧垂的方法是可行有效的，并且优于Bayes算法、KNN算法、决策树算法和BPNN算法. GA-SVM算法模型还有一些不足和待完善的地方，如引入更多和输电线路相关的属性特征，研究不同的SVM参数选择方法对实验精度的影响等.