一类SIR传染病模型的分岔分析

李明山， 张渝曼， 周效良

（岭南师范学院数学与统计学院，广东湛江524048）

近年来，传染病数学模型在研究传染病预防控制中发挥了重要作用.自Kermack与McKendrick于1927年在文献［1］中建立易感（Susceptible）-染病（Infective）-康复（Recovered）模型（简称 SIR 模型）以来，传染病模型的动力学研究取得大量的研究成果［1-14］.传染病数学模型应用于分析传染病的一般传播规律，对传染病的传播机制、流行规律和防控理论的相关研究具有重要理论意义.在学者们的研究下，在连续SIR传染病模型动力学研究中涌现出许多优秀的成果［2-7，9-11］.对于连续传染病模型而言，不仅仅要研究模型的稳定性，更要研究其分岔性质.因为稳定性仅仅说明了当时间趋于无穷模型解的性态，没有涉及模型的解受外界干扰时模型解的性态变化［2-3，5］.研究传染病模型分岔性质可以得到传染病模型的解受外界干扰时模型解的性态变化和传染病模型对应系统拓扑结构的变化与模型系数参数发生微小扰动时的关系，从而得到传染病模型的相关动力学性质［3-7，9-10］.故研究传染病模型的分岔性质对传染病的防控措施、传播机制与流行规律等相关理论研究是非常重要的.

1 模型介绍

在2012年，Wang等在文献［5］中研究了如下连续SIR传染病模型

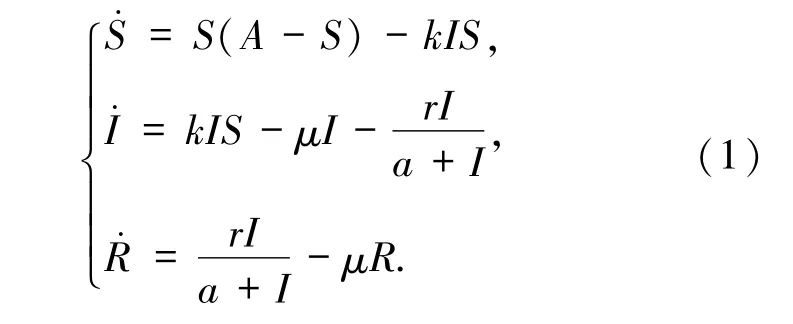
由于系统（1）前2个等式不含有R，所以只需考虑如下子系统

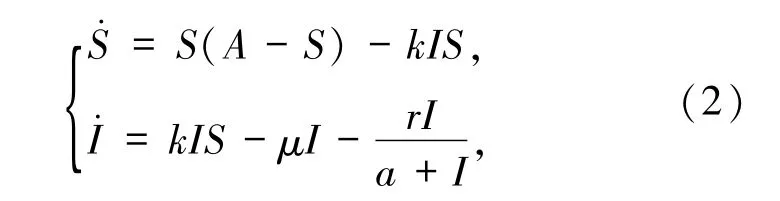
其中，S、I、R 分别代表易感者、染病者、康复者，k是感染率，μ是自然死亡率，r是康复率，a代表治疗措施对传染病传播的延迟效应.在文献［5］中假设模型（2）所有的系数参数均大于0.系统（2）有2个无病平衡点 E0（0，0）和 E1（A，0），系统（2）在 E1（A，0）处的Jacobi矩阵如下

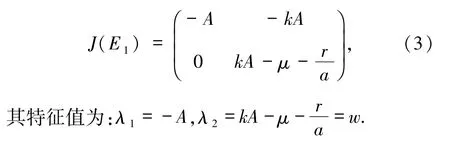
2 系统（2）的跨临界与音叉分岔

下面用中心流形定理来研究系统（2）在无病平衡点E1（A，0）处跨临界分岔和音叉分岔的性质与正规形.

证明 当 w ＝0时，有 λ1＜0，λ2＝0，为了体现系统（2）在无病平衡点E1（A，0）处的跨临界分岔对参数 w 的依赖，把 J（E1）写成 Jw（E1）；施行如下坐标变换，易知系统（2）在无病平衡点 E1（A，0）处的Jacobi矩阵为

特征值λ1、λ2对应的特征向量可以写成如下形式：

由变换（6）可以得到如下系统

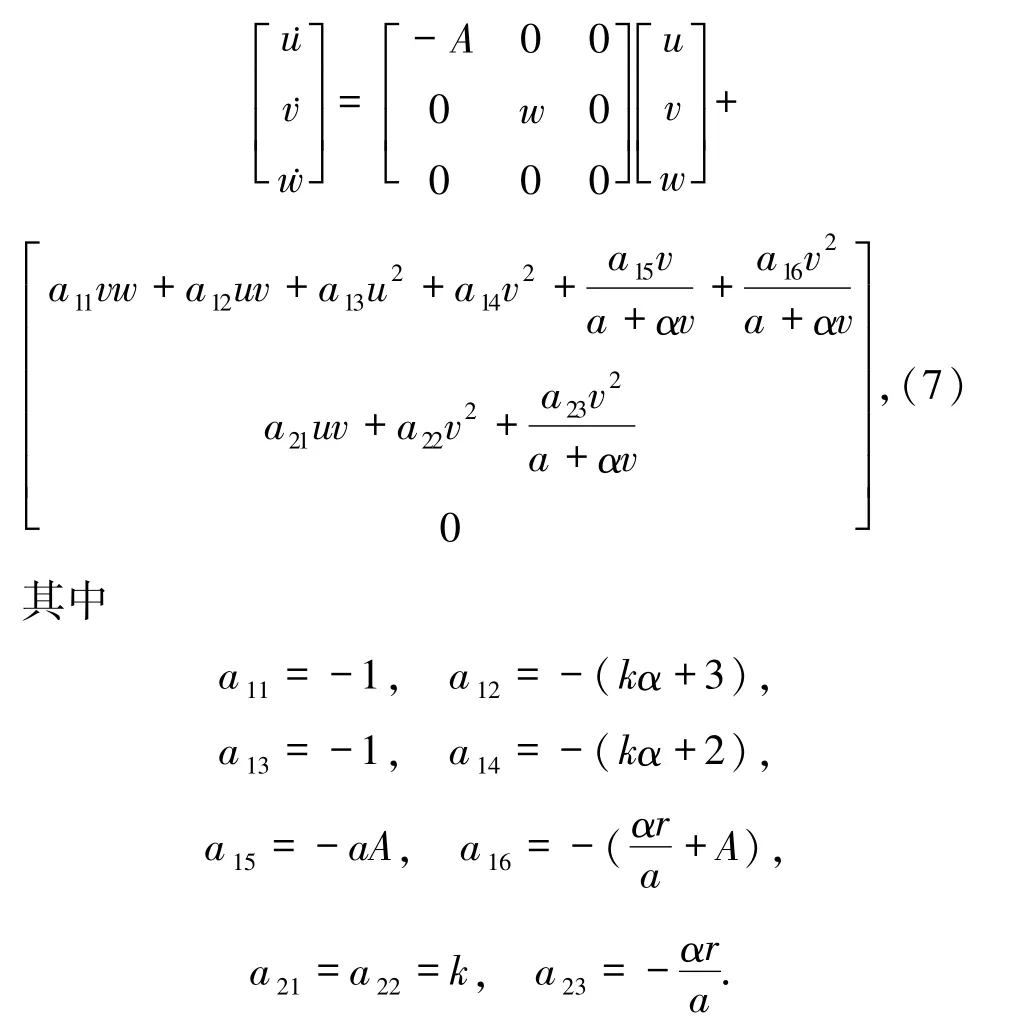
由引理2.1可知在w＝0附近系统（7）平衡点（u，v）＝（0，0）处的稳定性与分岔性质可通过中心流形上一参数系统来研究，由文献［15］中的定理18.1.2知中心流形具有如下形式

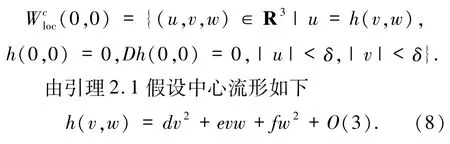
由引理2.1知可通过如下（9）式计算中心流形（8）：

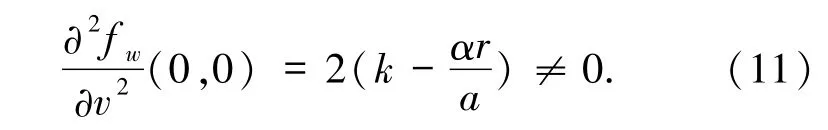
根据文献［15］可知系统（2）在 E1（A，0）平衡点处发生跨临界分岔，（11）式表明在（u，v）＝（0，0）附近所有高阶项O（3）不改变其分岔性质，亦表明在（u，v）＝ （0，0）附近系统（10）的拓扑结构与

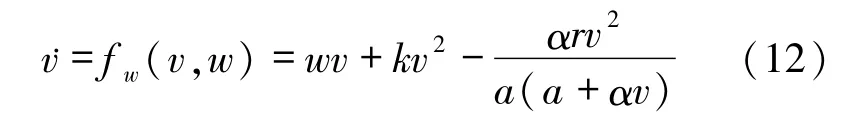
的拓扑结构是局部拓扑等价的.（12）式可以视作系统（2）在无病平衡点 E1（A，0）处跨临界分岔的正规形.

由文献［15］可知系统（2）在 E1（A，0）平衡点处发生音叉分岔.

（14）式可以视作系统（2）在无病平衡点 E1（A，0）处音叉分岔的正规形.

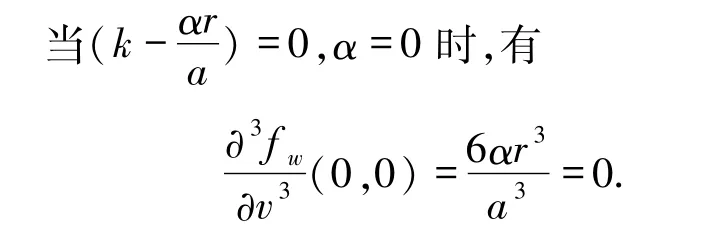
此时系统（2）在无病平衡点E1（A，0）处发生退化的音叉分岔.由

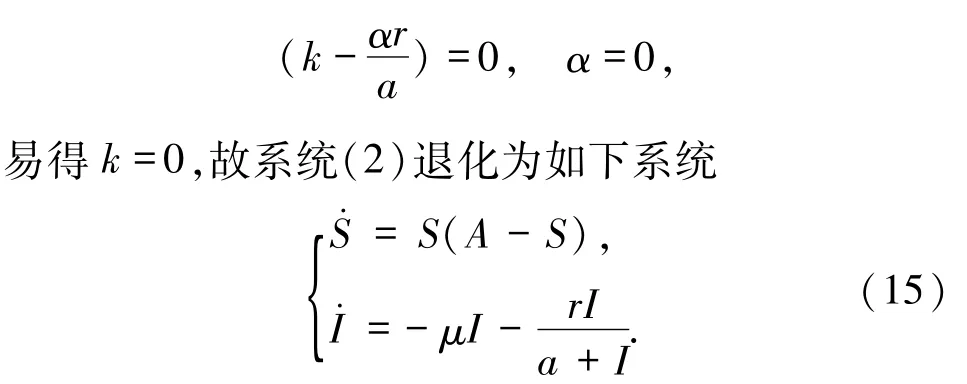
应用初等积分法可得

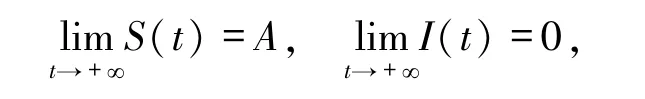
且系统（15）的每个等式都是独立的微分方程，所以系统（15）的轨道结构是清楚的.证毕.

3 分岔的生物学解释

由定理2.1 和2.2 可知，在 E1（A，0）处系统（2）的局部拓扑结构对参数w非常敏感，当w穿过0时，系统（2）平衡点 E1（A，0）的双曲性和稳定性都发生了改变，这表明传染病在种群中流行状态也发生了改变，故参数w在0附近的微小变化与传染病在种群中流行状态有着非常紧密的联系，此时系统（2）的拓扑结构与参数w在0附近的微小变化有着某种对应关系.这种对应关系对研究传染病的流行规律、传播机制和预防控制有重要的理论意义.人们可通过研究传染病模型的分岔性质来得到并且控制传染病模型的敏感参数，从而达到控制传染病在种群中流行状态的目的.

致谢 岭南师范学院攀峰计划项目对本文给予了资助，谨致谢意.