自制音叉的对称性与非对称性破坏性实验研究
2014-12-24方新艳王昆林
方新艳,王昆林
(楚雄师范学院,云南楚雄 675000)
音叉振动所发出的声波是纯音,其纯音的固有频率与叉股的长度、质量有关。理论上,改变音叉叉股长度会对音叉的振动频率产生影响,就这个问题,笔者用6圆(直径为6.0 mm)的建筑材料钢筋自制了一只叉股长度为52.00 cm的音叉,见图1,设计对自制音叉进行破坏性实验研究,探索其振动频率改变的状况,将其右叉股从顶端用钢锯截去2.00 cm,音叉成为非对称异型音叉,(左右叉股长度不一致)见图2,再将其左叉股截去2.00 cm,音叉成为对称正型音叉(两叉股长度一致对称),但双叉股长度变短,如此往复。利用DIS声传感数字化信息系统采集音叉各种情况的振动频率,在计算机上显示出频率随时间的变化图像;从而,对其展开对应性分析研究[1-7]。

图1 自制对称正型音叉

图2 自制非对称异型音叉
1 研究方案设计
采用DIS声传感数字化信息系统,测定自制音叉各种情况对应的频率,但因实验属于破坏性实验,各频率数据采集点不可逆,故采用标准音叉对DIS声传感数字化信息系统进行校正试测,实验装置如图3所示。以2.00 cm为步长,分别截断左右叉股,进行对应测试,进行对比研究。

图3 实验装置图
1 实验研究
1.1 标准音叉频率校正
选用一支频率为f0=512.00 Hz的标准音叉,按图3所示,联接好实验装置,敲击音叉叉股,使其振动产生声波。通过DIS系统可在计算机上得到如图4所示频率随时间变化的图像。
由图4可以得到,标准音叉振动所产生的声波为单一频率的纯音,其图像为标准的正弦图像,从图形横坐标上直接截取5个振动周期的时间间隔:0.009 8 s,从而得到标准音叉振动的周期:

标准音叉的频率:

取标准音叉的标称频率512.00 Hz为最佳近真值,则
Δf=(512.00 - 510.20)Hz=1.80 Hz,可算得相对误差为:
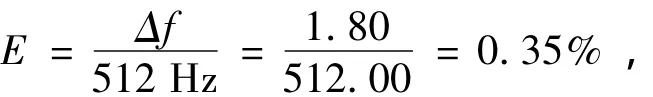
因为E很小,可忽略其对实验研究的影响。所以,用此方案研究自制音叉频率是可行的。

图4 标准音叉波形图
1.2 自制对称正型音叉频率研究
把自制对称正型音叉按图3联接好实验装置,敲击音叉叉股,使其振动产生声波。通过DIS系统可在计算机上得到如图5所示的图像。由图5可以看出,自制对称正型音叉振动所产生的声波为单一频率的纯音,也是标准的正弦波,故而可测到固定的频率值。

图5 自制对称正型音叉波形图
1.3 自制非对称异型音叉频率研究
把自制非对称异型音叉按图3联接好实验装置,敲击音叉叉股,使其振动产生声波。通过DIS系统可在计算机上得到如图6所示的图像。由图6可以看出,非对称异型音叉的声波波形图发生异变,并非标准的正弦图像。但是它依然具有规律性和周期性。也可测到固定的频率值。

图6 自制非对称异型音叉波形图
1.4 对称正型音叉非对称异型音叉交叉性频率研究
按上所述,以2 cm步长改变自制音叉的两叉股长度,并测出对应的振动频率,从而得到,自制对称正型音叉和自制非对称异型音叉的振动频率与叉股长度关系,分别见表1、表2。
用表1~2中的数据做出相应的关系图线,见图7~8。

图7 对称正型音叉叉股长度与频率关系图
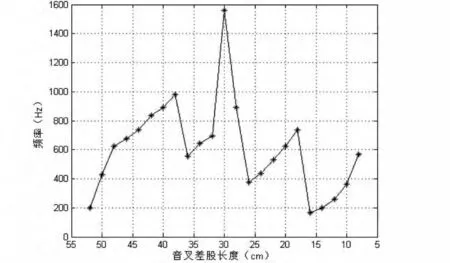
图8 非对称异型音叉叉股长度与频率关系图
2 分析研究
由表1及图7可以看出,对称正型音叉叉股长度在52.00~22.00 cm之间其振动频率随着叉股的减小而增大,但在叉股减小到22.00~20.00cm时音叉振动频率出现跳跃性的减小,叉股长度在20.00 ~10.00 cm之间,音叉的振动频率又随着叉股长度的减小而增大;在22.00 ~20.00 cm之间,音叉的振动频率突然减小,发生了突变,在变异点处22.00~20.00 cm。由于等步长和破坏性实验的不可逆,无法做更精细的探测。音叉频率突变可能是由于建筑钢筋在此处质量分布不均匀,以及直径分布不均匀等原因造成的。
由表2及图8可以看出,非对称异型音叉的叉股长度在52.00~38.00 cm之间,音叉的振动频率随着叉股长度的减小而增大,叉股长度在38.00~36.00c m音叉的振动频率随着叉股长度的减小而减小,叉股长度在36.00~30.00 cm之间,音叉的振动频率随着叉股长度的减小而增大,叉股长度在30.00~24.00 cm之间,音叉的振动频率随着叉股长度的减小而减小,叉股长度在24.00~18.00 cm之间,音叉的振动频率随着叉股长度的减小而增大,叉股长度在18.00~16.00 cm之间,音叉的振动频率随着叉股长度的减小而减小,叉股长度在16.00~8.00 cm之间,音叉的振动频率随着叉股长度的减小而增大。非对称异型音叉振动频率出现无规律的跳跃,整体上看,非对称异型音叉由于叉股的非对称性,不但引起振动波形异变,振动频率也无规律可寻。

表1 自制对称正型音叉的振动频率与叉股长度数据表

表1 自制非对称异型音叉的振动频率与叉股长度数据表
3 结 论
根据以上研究可以发现,对称正型音叉的频率与音叉叉股的长度有关。叉股长度减小音叉振动频率随之增大,它发出的声音和标准音叉发出的声音都是单音,所以,可以根据实际情况需要,改变其叉股长度,就可以改变其振动频率,从而,得到不同频率的音叉。非对称异型音叉振动频率无规律可寻,它发出的声音已不是纯粹的单音,从严格意义上讲,它已不是音叉。
[1]漆安慎,杜婵英.普通物理力学[M].北京:高等教育出版社,2005,6.
[2]侯俊杰.基于DIS系统测定自制音叉振动频率的研究[J].物理通报,2012(9).
[3]李会平.音叉负载金属环对其振动频率影响的实验研究[J].物理通报,2014(5).
[4]李定梅.基于计算机实测技术的音叉固有频率测量[J].物理实验,2010(11).
[5]盛翌航.基于Matlab的音叉声音信号的采集与分析[J].大学物理实验,2011(2).
[6]陈莹梅.音叉的共振频率与双臂质量的关系研究及其应用.物理实验,2006(7).
[7]周丽.用计算机研究音叉共振频率与双臂质量的关系.大学物理实验,2007(3).
