基于负载选择的非线性刚度驱动器性能评价

宋智斌，赵亚茹，高 冬，戴建生, 2



基于负载选择的非线性刚度驱动器性能评价

宋智斌1，赵亚茹1，高 冬1，戴建生1, 2

1. 天津大学机械工程学院机构理论和装备设计教育部重点实验室，天津 300072；2. 伦敦大学国王学院，伦敦 WC2R 2LS)

恒定刚度的串联弹性驱动器(SEA)的控制性能受刚度的限制，存在着系统安全性与带宽之间的矛盾．可变刚度驱动器(VSA)在一定程度上解决了高安全性与高控制带宽之间的矛盾，但其采用的刚度调节电机增加了结构的复杂性．基于“小负载，低刚度；大负载，高刚度”的人机交互策略的负载选择的非线性刚度驱动器(LDNSA)是一种新的具有良好应用前景的驱动方案．通过Simulink仿真和试验探讨了LDNSA在不同的刚度区间(不同的负载条件)的力矩控制性能，并与不同刚度的SEA的控制性能进行了比较分析．结果表明：与SEA相比，虽然LDNSA的力矩响应平稳性比低刚度的和高刚度SEA差，但LDNSA在负载较小时具有高安全性的同时依然能保证高的控制带宽，而负载较大时，LDNSA的控制带宽更高且力矩响应平稳性能增强．

非线性刚度；柔顺驱动器；控制性能；仿真；试验

串联弹性驱动器(series elastic actuator，SEA)在柔顺机器人人机交互应用中有诸多优点，如输出阻抗低、控制性能好、缓冲性能高等[1-3]，但这种驱动器的安全性和动力学性能往往受制于其固定刚度[4]，从而大大限制了驱动器的应用范围．在人机交互过程中过大的弹性刚度无法保证驱动器的安全性和力矩分辨力性能，相反，刚度太小会大大降低驱动器的控制精度和带宽等动力学性能[5]．

为了同时具有安全性和高的动力学性能，很多研究都转向了变刚度驱动器(variable stiffness actuator，VSA)[6-7]．VSA的刚度可以在一定范围内变化，通过低刚度和高刚度的转换调节在一定程度上实现了高的安全性和高的带宽性能平衡[8]．很多VSA通过增加额外刚度调节电机来实现驱动器刚度的调节[9]，增大了驱动器的体积和质量，导致了驱动器结构松散复杂[10]，不能应用在很多小型、轻型的机器人中．同时，这些VSA将刚度和交互力解耦，浪费了一些不必要的工作区间，例如，当负载力较大时，如果VSA调制到低刚度，其位置精度和带宽等动力学性能会大大降低[11]，所以在负载力较大时，为保证VSA的动力学性能，应选择高刚度的工作区间．相反，在负载较小时所需的刚度要尽量低．因为在人机交互过程中，驱动器的弹性元件需要在微小的负载力条件下依然产生一定的形变以检测交互力的大小，提高人机交互过程中驱动器对环境变化的灵敏度，进而提高人机交互的安全性[12-14]．而在负载力增大时其刚度也要相应增大以保证驱动器的位置控制精度和高的带宽性能[15]．

基于“小负载，低刚度；大负载，高刚度”的人机交互策略的负载选择的非线性刚度驱动器(load-dependent nonlinear stiffness actuator，LDNSA)是一种新的具有良好应用前景的驱动方案．但由于其在加载过程中刚度由低到高变化，所以与固定刚度的SEA相比，LDNSA在小负载时是否依然可以保证控制带宽等动力学性能是很多用户关心的问题．但是目前并没有关于可变刚度驱动器相对不同刚度的SEA表现的控制带宽和力矩响应平稳性等动力学性能的优劣的详细研究．本文从仿真和试验两个方面对LDNSA的控制性能进行评价，并从力矩控制带宽、力矩响应的平稳性和准确性等方面详细探讨了变刚度的驱动器相对于不同刚度SEA的控制性能的优劣，为非线性刚度柔顺驱动器的刚度设计和应用范围提供客观的参考，为变刚度驱动器刚度的优化提供一定的基础．

1 LDNSA结构设计和工作原理

LDNSA 包含电机组合(型号为397172的电机、型号为462003,12线的光电编码器和减速比为66∶1的减速齿轮)、丝绳、内外筒、弹性结构以及分辨力为0.005°型号为MSR5000的磁栅尺传感器(见图1).弹性结构由固定在外筒上的滚子和固定在内筒上的由两个对称的弹性元件构成的弹性体组成，以实现驱动器的反向驱动，见图2．如图3 LDNSA的原理图所示，电机组合作为驱动源和减速装置，通过丝绳将运动传递到外筒上．固定在外筒上的滚子与内筒上的弹性元件始终保持接触，从而外筒的运动得以有效传递到内筒上．当内筒承受外负载时，弹性元件和滚子存在相互作用力，弹性元件发生变形，内、外筒产生相对运动，该相对运动通过磁栅尺传感器测得．传感器和电机的信号由型号为TMS320F28335的DSP处理器处理后通过ESCON驱动器发射PWM波驱动电机．同时传感器与电机编码器的信号由MPS-010602采集卡采集并通过USB串口发送至PC机以供用户分析和处理试验数据，见图4．

图1 LDNSA的三维结构(剖视图)

图2 非线性刚度弹性体

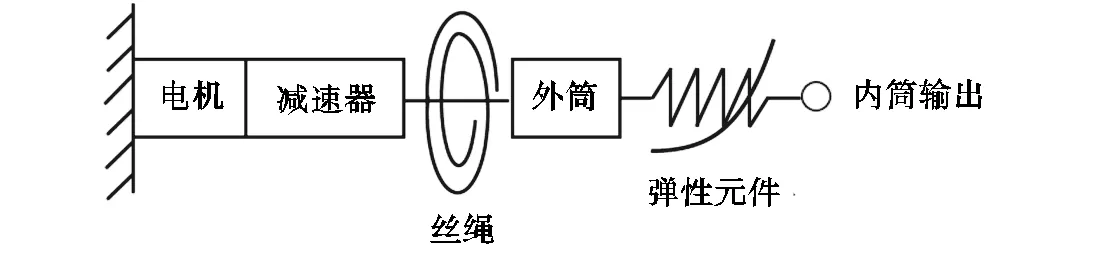
图3 LDNSA的原理

关于LDNSA非线性刚度的实现原理以及弹性结构的设计本课题组已在之前的文献[16]中做了详细描述，在此只简要阐明．弹性结构设计的核心是弹性元件的设计．弹性元件的设计以“小负载，低刚度；大负载，高刚度”的交互策略为基本思想，包括弹性单元(悬臂梁单元)和接触单元的设计．接触单元为刚性单元，在内外筒发生相对运动时，由于滚子与弹性元件的相互作用力，弹性单元产生挠度和挠角导致滚子与接触单元的接触点位置发生改变．滚子在径向上的位移受挠度和挠角的共同影响，所以其与接触力间的关系呈非线性特性．因此，通过弹性元件各部分尺寸和接触单元的轮廓设计可得到用户自定义的非线性刚度．

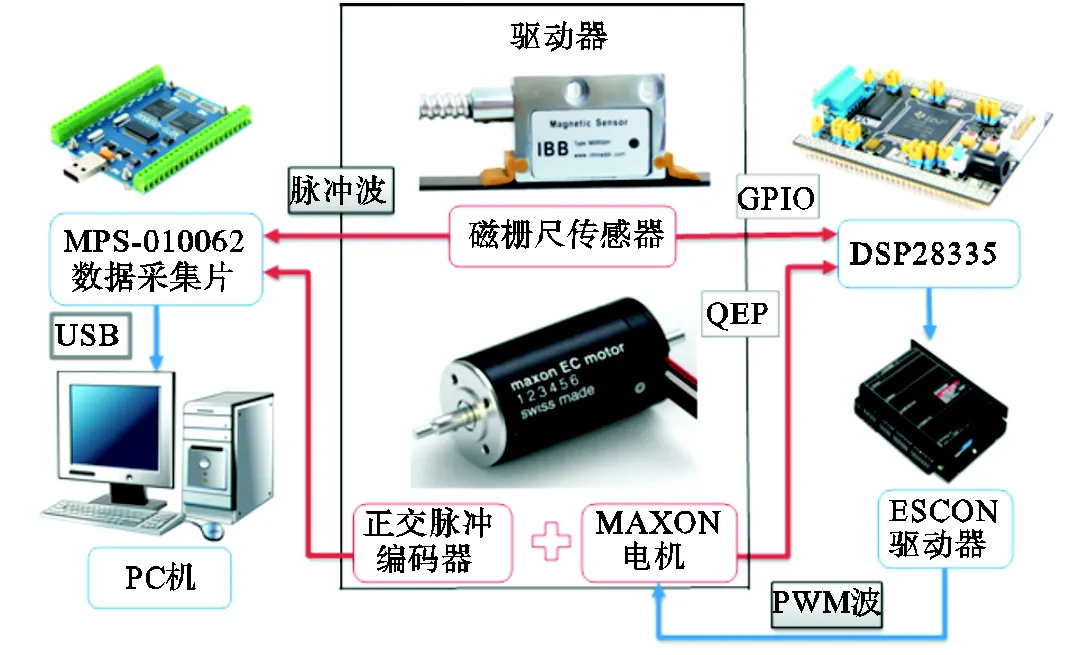
图4 LDNSA试验平台的原理

2 LDNSA控制性能评价

由于LDNSA的刚度随负载变化，所以其在不同的负载条件即不同的刚度区间内所表现的性能也存在差异，且由于其刚度从低到高(从高到低)变化，所以其与同等级刚度的SEA的性能在同样的负载下的异同依然需要探讨．笔者以LDNSA的系统为基础，当所设计的LDNSA的弹性元件的刚度为固定刚度时，LDNSA可以认为是固定刚度的SEA，通过仿真对不同刚度区间的末端固定的LDNSA的控制性能和相同系统条件下固定刚度的SEA的性能如控制带宽、力矩跟踪的平稳性和准确性进行分析比较，为不同的非线性刚度柔顺驱动器刚度的设计、优化和应用提供一定的参考．

2.1 LDNSA的动力学分析

图5 末端固定的LDNSA的运动模型

注：本文仿真时忽略电机、减速器、外筒的阻尼．

驱动器的运动可以用式(1)～(4)表示．

 (1)

 (2)

 (3)

 (4)

表1 LDNSA和SEA模型参数

Tab.1 Model parameters of LDNSA and SEA

驱动器模型电机惯量/(kg·m2)减速器惯量/(kg·m2)外筒惯量/(kg·m2)减速比传动比刚度/(N·m·rad-1) LDNSA66538.40～528.84 SEA66539，320，530

 (5)

2.2 LDNSA的力矩控制

与SEA不同的是LDNSA的刚度随力矩的大小变化，所以在LDNSA的力矩响应过程中，不同大小的力矩对应的刚度工作区间也不同．而典型的阶跃响应的最大超调和上升时间直观地反映了驱动器的力矩跟踪平稳性、准确性和响应速度[18]，阶跃响应的上升时间越短，驱动器的控制带宽越高[5]．本文中采用比例-微分(proportion-differentiation，PD)反馈控制器[19]，根据同样条件下的阶跃响应结果对LDNSA和SEA的控制性能如控制带宽和力矩响应的平稳性和准确性进行分析比较，为柔顺驱动器刚度的设计、优化和应用提供一定的参考．

 (6)

2.3 LDNSA和SEA的控制性能分析比较

在人机交互过程中，考虑到人体的承受力以及驱动器的柔顺性能，人机交互力一般小于10,N·m，并且很多柔顺驱动器的应用范围为0～10,N·m[2,13]，所以，本文研究LDNSA在0～10,N·m的力矩范围内的控制性能．LDNSA的力矩在0～10,N·m变化时，弹性元件的刚度在38.40～528.84,N·m/rad间变化．为分析比较不同力矩(即不同刚度区间)下LDNSA的控制性能和SEA性能的异同，本节选取SEA的刚度分别为39,N·m/rad、320,N·m/rad和530,N·m/rad，分别表示低、中、高刚度的SEA．

图7 LDNSA和不同刚度的SEA对不同负载的响应

表2 LDNSA和SEA的控制性能

Tab.2 Control performance of LDNSA and SEAs

在力矩为2,N·m、4,N·m、6,N·m、8,N·m、10,N·m时，低刚度(39,N·m/rad)的SEA产生的最大超调量分别为0.054,N·m(2.700%,)、0.107 N·m(2.675%,)、0.167,N·m(2.783%,)、0.225 N·m(2.812%,)、0.280,N·m(2.800%,)，上升时间分别为12.350,ms、12.520,ms、12.650,ms、12.630,ms、12.700,ms．由表2可知在相同的系统条件下，期望力矩越小低刚度的SEA产生的最大超调量与LDNSA产生的最大超调量差距越大，低刚度的SEA的响应过程更平稳，但其上升时间更长，响应速度较LDNSA大大降低．LDNSA能快速调节产生的超调，达到稳态的时间远低于低刚度的SEA．且在时间常数[20]范围内，LDNSA的响应曲线斜率远大于低刚度的SEA的响应曲线的斜率，说明与低刚度的SEA相比，LDNSA的阶跃响应速度更快，控制带宽更高．因此，与低刚度的SEA相比，LDNSA在人机交互过程中具有更快的响应速度，更高的控制带宽，虽然LDNSA的最大超调量较大，响应平稳性较差，但LDNSA能更快速地调节大的力矩误差，准确地达到稳定的期望力矩．

SEA的刚度取320,N·m/rad时的最大超调量分别为0.214,N·m(10.700%)、0.417,N·m(10.420%)、0.666,N·m(11.100%)、0.897,N·m(11.210%)、1.120,N·m(11.200%)，上升时间分别为6.226,ms、6.109,ms、6.186,ms、6.144,ms、6.124,ms．在力矩从2,N·m增大到6,N·m的过程中，中刚度的SEA的最大超调量低于LDNSA的最大超调量，平稳性能较好，之后随着力矩的增大，LDNSA的最大超调量快速减小，平稳性增强．这是由于在力矩为2,N·m、4,N·m、6,N·m时，LDNSA的刚度小于SEA的刚度，所以其最大超调量比SEA的最大超调量大，在力矩比较小时，其平稳性会比对应的SEA的平稳性差．但在对同一力矩的阶跃响应过程中，LDNSA的上升时间较短，有较好的快速性和较高的控制带宽性能，而且力矩越大时两者的上升时间差距越大，LDNSA的响应速度优势越明显．这是由于在力矩变大时，LDNSA的刚度也相应变大，在力矩超过6,N·m时其刚度比所选的SEA的刚度大，所以其在负载越大时快速性和高带宽性能优势表现得越明显．因此，虽然在负载较小时，中刚度的SEA在人机交互过程中具有更高的平稳性，但在负载较大时，固定刚度的SEA的局限性会越来越明显，LDNSA具有更高的控制带宽和力矩响应平稳性．

SEA的刚度为530,N·m/rad时，对2,N·m、4,N·m、6,N·m、8,N·m、10,N·m的力矩响应的最大超调量分别为0.052,N·m(2.600%,)、0.121,N·m (3.025%,)、0.157,N·m(2.617%,)、0.208,N·m (2.600%,)、0.280,N·m(2.800%,)，上升时间分别为6.298,ms、6.109,ms、6.337,ms、6.269,ms、6.313,ms．在高刚度的SEA进行力矩跟踪时，最大超调量较小，平稳性能较好，而由于LDNSA在阶跃响应过程中刚度小于530,N·m/rad，所以与高刚度的SEA相比其平稳性能较差．但是，LDNSA依然有很高的快速性和控制带宽性能，因为LDNSA在响应初始阶段刚度较小，对力矩的微小变化较敏感，驱动器得以及时做出响应以快速调整输出力矩．在小负载时LDNSA的最大超调量与高刚度的SEA差距较大，其力矩平稳性较差，但随着负载的增大，两者的最大超调量差距减小，在大负载时SEA在力矩平稳性方面并没有竞争性的优势．而在人机交互过程中LDNSA具有更高的控制带宽．

如图8所示，在人机交互过程中，与不同刚度的SEA相比，虽然LDNSA的平稳性比低刚度和高刚度的SEA差，但LDNSA的上升时间较短，具有较高的控制带宽，在相同的系统条件下，LDNSA能更快地调节力矩跟踪误差以使系统快速而准确地达到期望的力矩．在低刚度时，LDNSA能够在实现高安全性的同时保持相对高的控制带宽性能，随着刚度增大，快速性能增强，控制带宽性能的优势越来越明显．

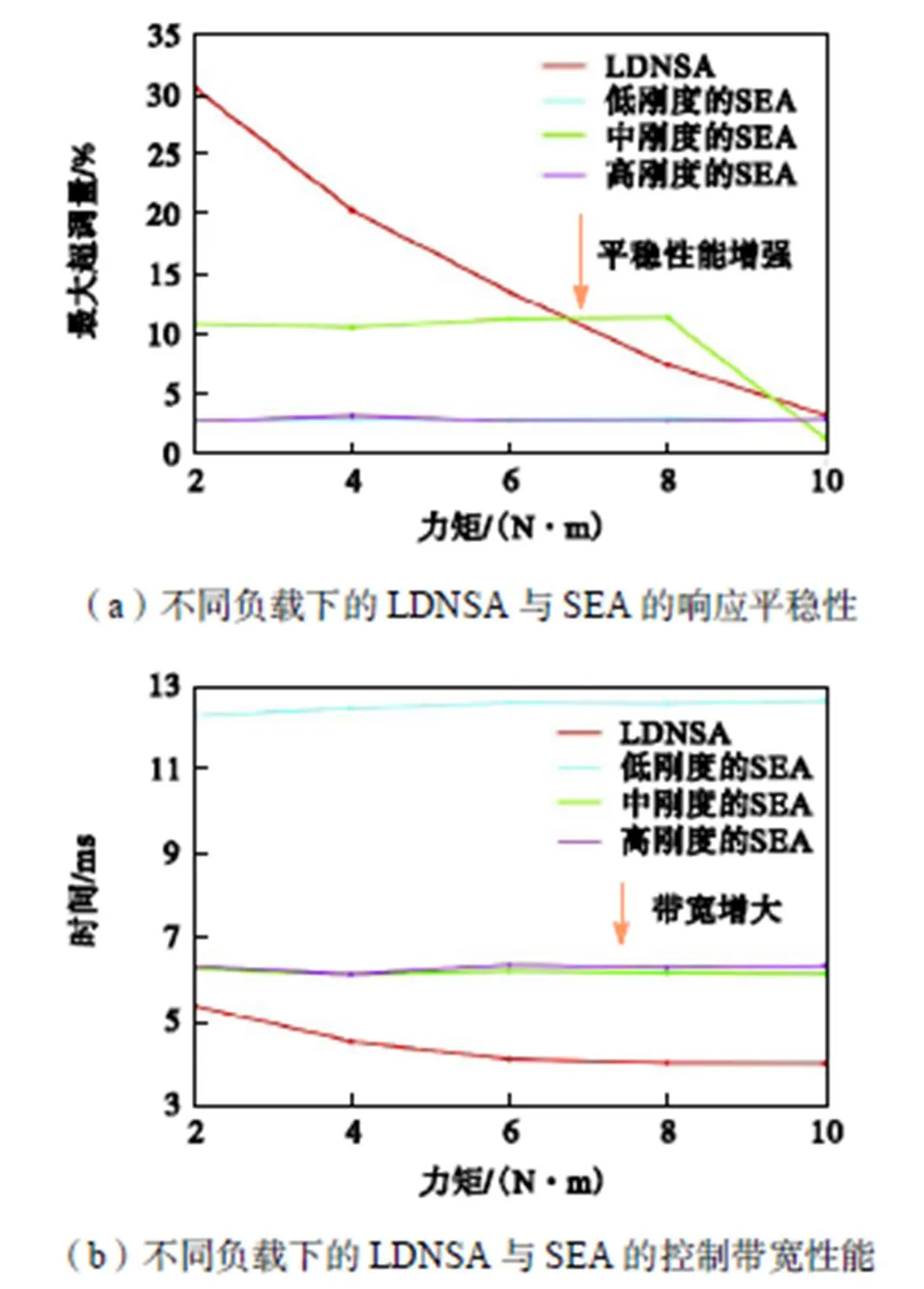
图8 LDNSA和不同刚度SEA的控制带宽和平稳性比较

3 试验验证

图9(a)表示力矩为2,N·m时LDNSA的跟踪效果，由于在力矩较小时，驱动器的刚度较小，柔度较高，驱动器响应过程中存在轻微的振荡，最大超调为0.180,N·m，即驱动器的最大跟踪误差为9%,，但此误差可以通过PD控制器很快地消除从而准确地达到期望的力矩．力矩响应曲线的上升时间为64.5,ms，考虑到实际的摩擦、迟滞等不可避免的影响因素，虽然试验数据与仿真结果存在差异，但现实操作中，依然可以证明LDNSA的响应速度较快、控制带宽较高的特性[21]．图9(b)表示力矩为8,N·m时LDNSA的跟踪效果．LDNSA在跟踪较大的力矩时响应过程较平稳，几乎不存在振荡．曲线的上升时间为50,ms，由于力矩较大时驱动器刚度较大，所以响应速度比低刚度时的响应速度更快，控制带宽更高．从试验结果的分析可知，LDNSA在实际操作过程中可快速而准确地跟踪给定的不同大小的负载，且在负载较大时，LDNSA的响应过程不存在振荡，平稳性能较好．

图9 LDNSA对不同负载的力矩响应试验

4 结 论

(1) 本文针对LDNSA的非线性刚度特性，通过仿真对LDNSA的控制带宽和力矩响应平稳性等控制性能进行评价，可知在人机交互过程中，LDNSA具有高带宽性能，同时随着负载的增大，LDNSA的力矩响应平稳性能增强．

(2) 通过仿真将LDNSA的控制性能与相同系统条件下不同刚度的SEA的控制性能进行了对比. 反映出虽然非线性刚度驱动器对小负载的响应平稳性比SEA差但其控制带宽远远高于SEA，且LDNSA能更快速地调节大的力矩误差，准确地达到期望的力矩，在负载较大时，非线性刚度驱动器高的控制带宽优势更明显且平稳性能良好．

(3) 通过试验验证了驱动器对大、小两种负载的跟踪性能，反映出驱动器响应速度快、力矩跟踪准确性高的特点，并且刚度由低到高时，驱动器的响应速度加快且响应平稳性提高．

［1］ Robinson D W，Pratt J E，Paluska D J，et al. Series elastic actuator development for a biomimetic walking robot[C]///. Atlanta，GA，USA，1999：561-568.

［2］ Austin J，Schepelmann A，Geyer H. Control and evaluation of series elastic actuators with nonlinear rubber springs[C]///Hamburg，Germany，2015：6563-6568.

［3］ Kong K，Bae J，Tomizuka M. A compact rotary series elastic actuator for human assistive systems[J]./，2012，17(2)：288-297.

［4］ Zinn M，Khatib O，Roth B，et al. A new actuation approach for human friendly robot design[J].，2008，1：379-398.

［5］ Schepelmann A，Geberth K A，Geyer H. Compact nonlinear springs with user defined torque-deflection profiles for series elastic actuators[C]//Hong Kong，China，2014：3411-3416.

［6］ Awad M I，Gan D，Cempini M，et al. Modeling，design & characterization of a novel passive variable stiffness joint(pVSJ)[C]///Daejeon，South Korea，2016：323-329.

［7］ Rodríguez A G，Chacón J M，Donoso A，et al. Design of an adjustable-stiffness spring：Mathematical modeling and simulation，fabrication and experimental validation[J].，2011，46(12)：1970-1979.

［8］ Tonietti G，Schiavi R，Bicchi A. Design and control of a variable stiffness actuator for safe and fast physical human/robot interaction[C]//. Barcelona，Spain，2005：526-531.

［9］ Jafari A，Tsagarakis N G，Caldwell D G. A novel intrinsically energy efficient actuator with adjustable stiffness(AwAS)[J]./，2012，18(1)：355-365.

［10］ Accoto D，Carpino G，Sergi F，et al. Design and characterization of a novel high-power series elastic actuator for a lower limb robotic orthosis[J].，2013，10(359)：1-12.

［11］ Erler P，Beckerle P，Strah B，et al. Experimental comparison of nonlinear motion control methods for a variable stiffness actuator[C]//Sao Paulo，Brazil，2014：1045-1050.

［12］ Sariyildiz E，Chen G，Yu H. An acceleration-based robust motion controller design for a novel series elastic actuator[J].，2016，63(3)：1900-1910.

［13］ Paine N，Mehling J S，Holley J，et al. Actuator control for the NASA-JSC valkyrie humanoid robot：A decoupled dynamics approach for torque control of series elastic robots[J].，2015，32(3)：378-396.

［14］ Wolf S，Eiberger O，Hirzinger G. The DLR FSJ：Energy based design of a variable stiffness joint[C]//Shanghai，China，2011：5082-5089.

［15］ Migliore S A，Brown E A，Deweerth S P. Novel nonlinear elastic actuators for passively controlling robotic joint compliance[J].，2007，129(4)：406-412.

［16］ Lan S，Song Z. Design of a new nonlinear stiffness compliant actuator and its error compensation method [J].，2016，2016：1-8.

［17］ Ruderman M，Iwasaki M. Control of nonlinear elastic joint robots using feed-forward torque decoupling[J].，2015，48(11)：137-142.

［18］ Wang F，Liang C，Tian Y，et al. Design and control of a compliant microgripper with a large amplification ratio for high-speed micro manipulation[J]./，2016，21(3)：1262-1271.

［19］ Losey D P，Erwin A，Mcdonald C G，et al. A time-domain approach to control of series elastic actuators：Adaptive torque and passivity-based impedance control [J]./，2016，21(4)：2085-2096.

［20］ Sergi F，O’Malley M K. On the stability and accuracy of high stiffness rendering in non-back drivable actuators through series elasticity[J].，2015，26：64-75.

［21］ Lee Y F，Chu C Y，Xu J Y，et al. A humanoid robotic wrist with two-dimensional series elastic actuation for accurate force/torque interaction[J]./，2016，21(3)：1315-1325.

(责任编辑：金顺爱)

Performance Evaluation of Load-Dependent Nonlinear Stiffness Actuator

Song Zhibin1，Zhao Yaru1，Gao Dong1，Dai J S1, 2

(1. Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education， School of Mechanical Engineering，Tianjin University，Tianjin 300072，China； 2. King’s College London，University of London，London WC2R 2LS，United Kingdom)

The control performance of series elastic actuator(SEA)with constant stiffness is limited by stiffness leading to the contradiction between safety and bandwidth. Variable stiffness actuator(VSA)solves the contradiction between high safety and high control bandwidth in some degree，but the motor is employed to adjust stiffness complexes its structure. Considering the disadvantages of SEA and VSA，a load-dependent nonlinear stiffness actuator(LDNSA)was introduced to apply in the human robot interaction(HRI)based on the HRI strategy of“Small load，low stiffness；large load，high stiffness”. The torque control performance of LDNSA under different stiffness ranges/different loads was discussed through simulation and experiment and was compared with that of SEAs with different stiffnesses. It was obtained afterword that：Compared with SEA，although the stability of torque response of LDNSAis worse than SEAs with low stiffness and high stiffness，LDNSA achieves high control bandwidth along with high safety under small load，while LDNSA has higher bandwidth and better torque response stability under large load.

nonlinear stiffness；compliant actuators；control performance；simulation；experiment

the Key Program of the Natural Science Foundation of Tianjin，China (No.,17JCZDJC30300)，the Natural Science Foundation of China(No.,51475322，No.,51535008，No.,51775367 and No.,51721003)and the Program of Introducing Talents of Discipline to Universities(No.,B16034)．

TP242.3

A

0493-2137(2018)11-1117-07

2018-03-08；

2018-06-12.

宋智斌（1983—  ），男，博士，副教授.

宋智斌，songzhibin@tju.edu.cn.

天津市自然科学基金重点资助项目(17JCZDJC30300)；国家自然科学基金资助项目(51475322，51535008，51775367，51721003)；教育部高等学校学科创新引智基地资助项目(B16034).

10.11784/tdxbz201803027