耗散修正的Camassa-Holm方程解的存在唯一性
2018-11-07,
,
(浙江理工大学理学院,杭州 310018)
0 引 言
本文主要考虑修正的Camassa-Holm方程的Cauchy问题,该问题可以描述为:
mt+auxm+bumx=0,t>0,x∈R
(1)
u(x,0)=u0(x),x∈R
(2)
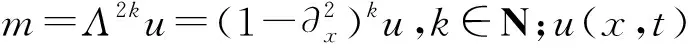
修正的Camassa-Holm方程是作为不变的Hk空间中扩散自同态群的测地线方程,由Constantin等[1-2]导出。当a=2,b=1,k=0或者1时,方程(1)分别为KdV方程和Camassa-Holm方程,其中Camassa-Holm方程的形式为:
ut-uxxt+3uux=2uxuxx+uuxxx
(3)
它最早是被Fokas等[3]提出,直到Camassa等[4]将其作为浅水波模型才被认真研究。方程(3)从被研究以来,许多人都在关于它的适定性方面做出了贡献,例如,Constantin[5]、Constantin等[6]以及Misiolek[7]分别讨论了s≥4,s≥3和s>3/2时关于初值在Hs(S),S=[0,2π]上的局部适定性;在非周期情况下,Li等[8]证明了初值在Hs(R)(s>3/2)上解的局部适定性。关于修正的Camassa-Holm方程(1),Malachlan等[9]研究了其解的适定性以及弱解的存在性,他们证明了周期的Cauchy问题在空间Hs(s>7/2)上是局部适定的,并且解持续依赖于初始值;在非周期情况下,Mu等[10]研究了解在Hs(R)(s>7/2)空间的局部适定性问题,并且证明了解依然持续依赖于初始值。Fu等[11]研究了方程(1)的Cauchy问题并且证明了解在Hs(R)(s>7/2)空间不一致连续。
类似修正的Camassa-Holm方程,Escher等[12]推导了一个二元修正的Camassa-Holm方程组:
(4)

以上研究表明,无论是修正的Camassa-Holm方程,还是二元修正的Camassa-Holm方程组,当r=2时其解的存在空间Hs(R)都要求s>7/2。本文通过对修正的Camassa-Holm方程添加耗散项,利用半群性质、非线性估计、缩映射原理及能量估计,改进了已有的解的适定性,建立了其在低正则性空间中解的存在唯一性。
1 主要定理
本文考虑修正的Camassa-Holm方程在低正则性空间中解的存在唯一性,给定初值u0∈L2(R),建立如式(5)描述的耗散修正的Camassa-Holm的适定性问题:
(5)

(6)
其中:

本文提出的主要定理如下:
定理1对于u0∈L2(R),存在T>0,方程(6)存在唯一的解u满足
u∈C([0,T]:L2(R))∩L2((0,T):H2(R)).
定理2对于u0∈H2(R),有任意的T>0,当a=2,b=1时方程(6)存在解u满足
u∈C([0,T]:L2(R))∩L2((0,T):H2(R)).
最后,本文给出Lp(Rn)空间和Hs(Rn)空间的定义及其范数形式:设p为非负实数,则定义Sobolev空间Lp(Rn)为:
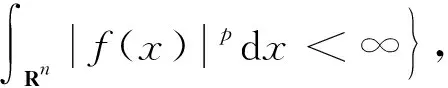
Lp(Rn)空间f(x)的范数为:
设s为非负实数,则定义Sobolev空间Hs(Rn)为:

Hs(Rn)空间f(x)的范数为:
2 非线性估计
考虑方程(6)所给出的初值问题,其中它的积分形式为:

(7)


(8)
证明由f(u)的表达式,再结合Sobolev嵌入定理[16]有
其中,右边第四项的估计为:


其中,F[·]表示对·做傅里叶变换。再由Hölder不等式有

(9)
证明结合引理1即可证明引理2成立。
引理3考虑线性方程
(10)

(11)
证明在方程(10)两边同乘ω并在R上对x积分可得:
两边同时对t从0到T积分可得:
则可得到上式的估计为:
即证明了引理3。

(12)
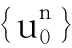
由引理3得:

(13)
对∀δ>0,N∈N,则对任意的n>N有
再取T>0,对使得n≥N有
综上所述,对∀δ>0,∃T>0,使得
方程(7)的非线性部分的估计为:
令v=u-s(t)u0,则v可以看作是如下初值问题的解,
(14)
方程(14)的积分形式表示为:

(15)
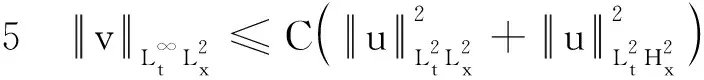
(16)
(17)
证明先证式(16)成立,

由引理2可知式(16)成立。
式(17)的证明为:
方程(14)两边同乘v并在R上对x积分可得
两边同时对t从0到T积分可得

则对任意的ε>0,有

则有


(18)
证明通过引理2-5,有

3 适定性
利用压缩映射原理证明解的存在唯一性,如此令

(19)


(20)


(21)
通过引理2及引理6,得

(22)

(23)
联立式(22)—(23),得到

选取适当的δ,a,T有

类似可以得到:

(24)

综上即证明定理1成立。
证明定理2,首先有能量估计为:
引理7对于u0∈H2,当方程(6)中a=2,b=1时,有
(25)
证明当a=2,b=1时,方程(6)为:

(26)

(27)
两边同乘u并在R上对x积分可得

由H2守恒率有

则有
因为
所以
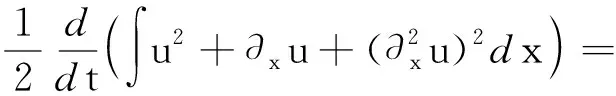
从而证明了引理7成立。
结合定理1及引理7的证明,就可以得到方程(26)存在全局解,则证明了定理2。
