结合稀疏理论与非下采样剪切波变换的多模态医学图像融合算法

，，

(1.浙江理工大学机械与自动控制学院，杭州 310018；2.浙江工商大学信息与电子工程学院，杭州 310018)

0 引 言

近年来，高精度成像技术的不断发展，给临床医学的诊断与治疗带来了巨大便利。然而，由于临床医学领域的特殊性，要求图像不但能够呈现直观的器官轮廓，而且要有清晰的纹理效果，依靠单模态图像很难达到这些要求[1-2]。比如，CT图像能够反映密度较大的骨骼结构，但对密度较小的组织缺乏清晰成像的能力；相反，MRI图像只适用于显示密度较小的组织，而对于大密度的骨骼结构的显示明显不适用。因此，为便于临床医学诊断，需要对单一模态图像取长补短，进行多模态的医学图像融合。

医学图像融合算法种类众多，就分解工具而言，主要有小波变换、轮廓波变换以及剪切波变换等。与剪切波变换相比，小波变换[3]线奇异性较差，对二维图像信息的捕捉能力不足，容易产生伪吉布斯现象；而轮廓波变换[4]算法相对复杂，运行效率不高。这两种变换在计算复杂度、运行效率、捕捉结构信息能力等方面均逊于剪切波变换[5]。由于传统的剪切波变换存在下采样操作，为防止出现伪吉布斯现象，人们对其进行改进，提出了非下采样剪切波变换[6](Non-subsampled shearlet transform , NSST)。

NSST优势明显，应用简便，近年来已逐渐成为研究的热点。如Cao等[7]和Padma等[8]利用NSST进行医学图像融合，与传统方式相比，这类方法在融合图像在纹理、清晰度、亮度以及对比度等方面都获得了一定的改进，但通过NSST获得的低频系数近似为零项极其有限，即对于图像的低频系数信息无法稀疏的表示，若对其进行直接融合处理，会对图像重要特征的提取带来不便，结果将会造成低频子带在融合处理过程中无法最佳的获取图像中理想位置的信息。

在图像融合处理中，研究人员希望尽可能地提高图像子带系数的稀疏度并利用较少的信息获得最优的融合结果，因此研究者关注到了稀疏理论。Yu等[9]、Shahdoosti等[10]以及Yin等[11]成功将稀疏理论与字典学习思想应用到图像融合处理过程中，有效提高了子带系数的稀疏度，但稀疏融合处理是在单尺度基础上对源图像进行直接训练，虽然能够对源图像中的重要特征进行提取，但对于多尺度数据的分析能力有限。稀疏理论与多尺度分析的有效结合，既能满足提取图像显著特征的要求，又可以提高数据分析能力，使得融合图像达到医疗诊断对清晰度的要求。

基于以上分析，为提高图像系数的稀疏度，增强视觉效果，进一步凸显图像的细节信息，本文结合NSST和稀疏理论对源图像进行处理。首先，通过NSST滤波器分解源图像得到高低频子带系数，其中高频子带包含源图像的纹理和细节等重要的信息，低频图像作为源图像的近似图像；其次，低频区域融合通过稀疏理论的方法来改善其较差的稀疏性，高频系数处理采用相对标准差比较法(Relative standard deviation comparison method，RSDC)，通过对相对标准差以及能量值的求取来选择最终的融合高频系数；最后，将低高频的融合系数通过NSST逆变换得到最终的融合图像，并通过空间频率(Spatial frequency, SF)、标准差(Standard deviation, SD)、平均梯度(Average gradient, AG)、边缘信息评价因子 (Edge based similarity measure , QABF)、结构相似(Structure similarity, SSIM)等客观指标对融合后的图像进行评价。以上几个客观评价指标值越大，表明图像融合效果越好，指标定义见文献[12]。

1 剪切波及稀疏理论

1.1 剪切波理论

剪切波以合成小波理论为基础，结合仿射系统和多尺度分析构建模型。当维数n=2时，其定义式为:

(1)

(2)

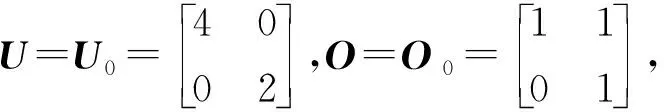
NSST操作主要分为两个步骤，即多尺度剖分以及方向局部化。多尺度剖分主要是源图像经过滤波器以及金字塔组分解成j+1个子带，其中一个低频子带和j个高频子带;方向局部化：标准化的剪切波分解器在经过从伪极网格系统到笛卡尔系统变换以及傅里叶变换，卷积等相关运算即可实现非下采样剪切波的方向局部化。图1是NSST的3层分解图，源图像经过第一层分解就得到两个分支，其中一个分支为低频子带，另一分支为高频子带，要获得图像的多层分解，需要对上一层分解得到的低频子带继续分解即可。NSST的支撑基是形状为梯形的一对区间，如图2所示，每个梯形区间宽度为22j，高度为2j。

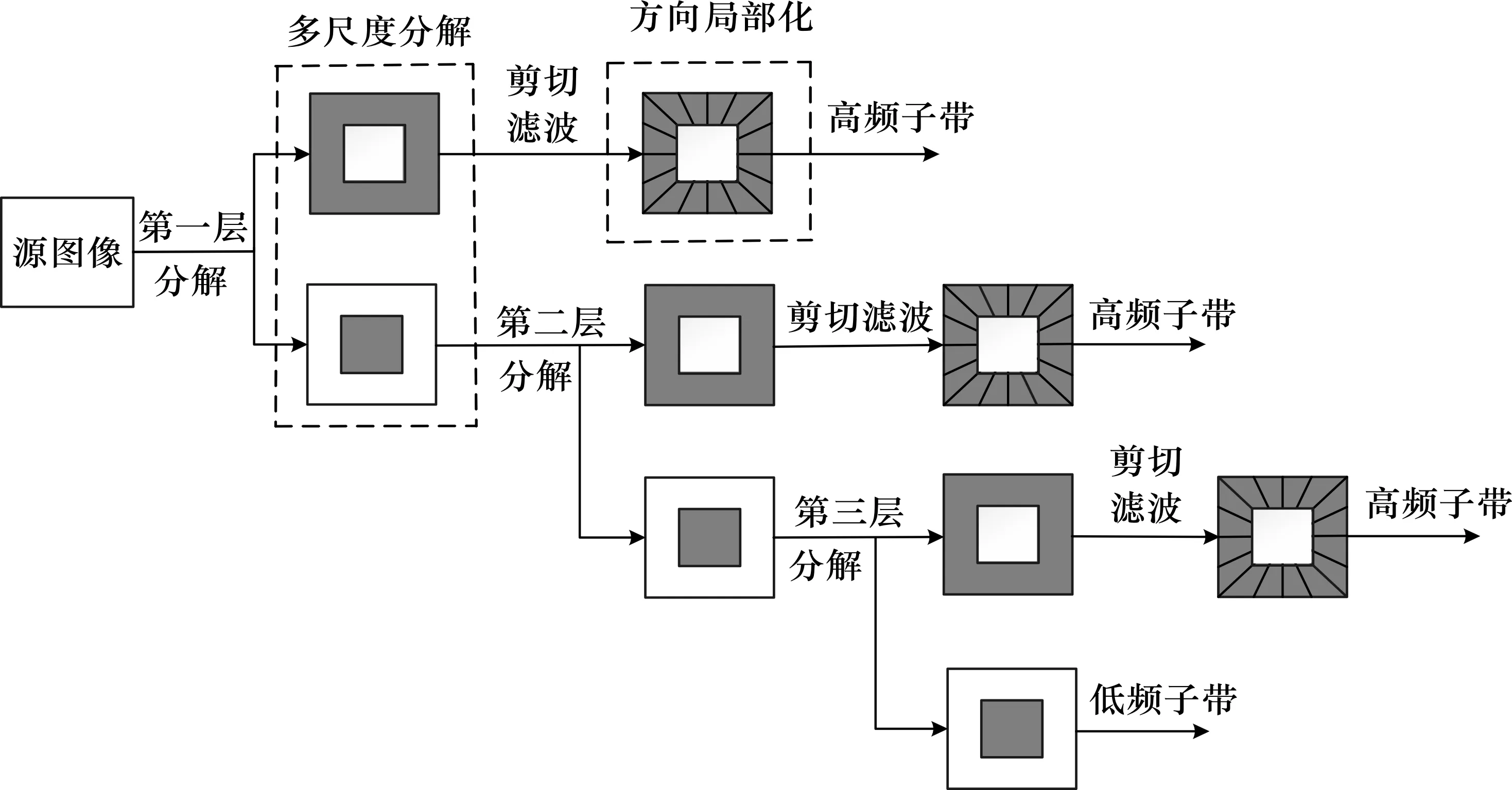
图1 NSST分解

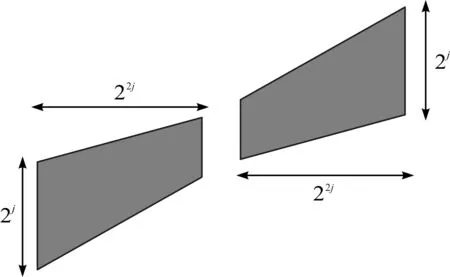
图2 NSST梯形支撑区间

1.2 稀疏理论

近年来稀疏理论日益完善，在图像处理领域得到了广泛的应用。稀疏表示主要是将图像领域明显的结构信息聚集到字典中较少的原子图像，而原子图像的集成可以构成一个过完备的字典，由于该字典具有冗余性，信号可以凭借字典中少量原子的线性组合来表示，该表示中原子数目最少的表示即为稀疏表示，其数学模型可以表示为：

(3)

上述稀疏模型中最关键的是字典选择，而常规方法主要包括学习方式和解析方式两种，其中学习方式主要通过ODL算法、K-SVD算法等算法来训练过完备字典，使其形态丰富，匹配图像结构良好。本文通过K-SVD算法来训练字典，其目标优化函数如下

(4)

其中:Y=[y1,y2,…,yN]∈Rn×N为样本训练矩阵;X∈Rn×N为稀疏系数矩阵,Xi为X的第i列的稀疏系数矩阵;T为稀疏度。

由于图像高频领域信息较少，冗余较多，为改善图像融合后的效果，本文在图像低频领域进行字典学习，式(4)可等价为:

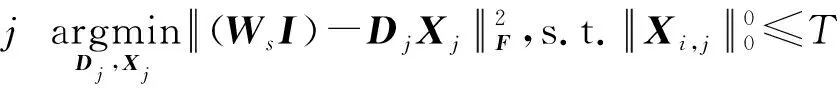
(5)

其中：Ws表示分析变换因子；I为图像训练矩阵。

通过上述方式构建出的学习字典能够对稀疏度不高的图像低频领域进行稀疏表示，使得学习字典具有NSST的分析能力，同时，对NSST低频系数的再次稀疏，可以实现双重稀疏，进一步提高低频领域的稀疏度，以更好地提取图像的相关特征。

2 NSST与稀疏理论相结合的融合算法

本文融合策略主要分为三个步骤。首先，利用NSST分解待融合的图像，得到不同频率的系数子带；其次，根据不同频率系数子带自身的不同特性设计相应的融合规则。由于低频子带反映源图像的轮廓，包含了源图像的大量能量，但其稀疏性不佳，融合后的图像效果较差，因此为提高其稀疏度，本文引入稀疏理论对低频区域进行处理；而图像的高频区域则反映源图像的细节信息，因此为凸显其局部细节，本文通过相对标准差比较法进行判断选取。最后，将低高频区域各自的融合结果通过NSST重构，获得最终的融合结果。具体融合框架图如图3所示，源图像经过NSST分解成低高频子带，低频子带融合通过训练字典，稀疏表示等步骤进行处理，高频子带则通过相应规则进行融合，处理后的低高频子带系数经过NSST逆变换得到融合图像。

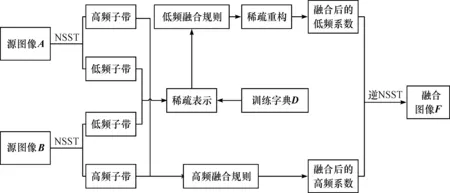
图3 融合框架图

2.2 融合策略

2.2.1 基于稀疏理论的低频系数融合算法

图像的轮廓信息主要集中在低频子带系数中，传统低频的融合方案如方差取大法、梯度加权法、空间频率加权法等方法基本能够较好保留源图像的轮廓信息，但都无法有效改善低频系数较差的稀疏性，导致最终的融合效果不够理想，因此，为提高其稀疏度，改善融合效果，本文将稀疏理论应用到图像低频子带融合处理中。相对于传统方法，本文稀疏理论的算法不但顾及了源图像的轮廓，而且使其稀疏度得到了有效提升，此外，该算法也使融合图像的清晰度和亮度得到了一定的改善，融合的效果较为理想。具体方法为:

a) 利用NSST分解配准后尺寸为M×N的源图像A和B得到低频子带系数gLA(i,j)和gLB(i,j),利用大小为n×n的滑动窗口分别对两图的低频子带进行分块处理,得到数量为(N+n-1)×(M+n-1)的图像子块，将所获得的图像子块转换为列向量,从而得到样本训练集矩阵VA和VB;

c) 依据式(4)理论采用K-SVD算法对VAS和VBS进行训练，得到过完备字典D;通过OMP算法预估两样本稀疏矩阵VAS和VBS的稀疏系数，得到矩阵αA和αB;

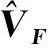
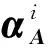
(6)

(7)

(8)

(9)

(10)

e) 将式(10)中VF的列向量重新转换为子块，重构该子块即可得到融合后的低频子带系数。

2.2.2 高频子带系数融合

医学诊断领域为便于对微小细节的观察，减少误判，要求图像的边缘纹理尽量清晰，而传统处理方式如区域能量法、边缘强度取大法、区域对比度法等存在细节处理模糊不清和边缘带撕裂等问题，因此，为改善视觉效果，便于医学诊断，本文提出了一种相对标准差比较法。相对于传统方式，本文高频融合方法不但有效弥补了这些方法的不足，而且使得高频区域的边缘点更加突显，边缘信息的丰富性更优，融合图像的边缘带更加明了，对于医学判断更加有利。具体步骤如下：

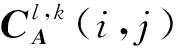
相对标准差是衡量图像融合效果的重要指标，其值越小，表明融合图像越清晰，图像的融合效果越好。此处为便于计算，区域窗口大小设为3×3 ,相对标准差定义式如下：

(11)

其中:M∈{1,2}。若M值为1，则I(i,j)表示源图像在(i,j)处的高频系数；若M值为2，则I(i,j)表示融合图像在(i,j)处的高频系数。

此处能量值是用于衡量图像边缘化程度高低的重要指标，若能量值越大，图像就越清晰，融合效果也就越好，具体公式为：

E(x,y)=∑(i,j)∈Ω(x,y)P2(i,j)T(i,j)

(12)

其中：Ω(x,y)是以(x,y)为中心的区域窗口，P(i,j)为区域差值绝对值系数,T(i,j)则是对应的窗口矩阵。

为了突出系数变化剧烈的程度，增强对比度，提高融合质量，此处窗口矩阵T(i,j)设为

(13)

T中元素数值相差相对较大，可以处理系数变化剧烈的区域。

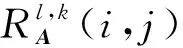
(14)

α(i,j)=

2.3 图像融合步骤

本文图像融合具体过程有以下几个步骤：

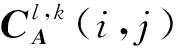
b) 采用K-SVD算法对低频子带进行样本训练。

c) 利用大小为n×n的滑动窗口分别对低频区域进行分块处理，对获得的图像子块序列进行优化，并结合OMP算法进行预估，得到稀疏系数矩阵αA和αB;通过稀疏矩阵αA和αB,样本训练字典矩阵D以及样本均值矩阵进行处理并将融合矩阵重新转化为图像块即可得到融合后的低频子带系数GL(i,j)。

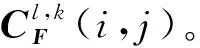
e) 将上述融合结果进行NSST重构逆变换，得到融合结果图像F;选择相关评价指标对融合后的图像从定性和定量角度进行分析。

3 图像结果分析

为验证本文算法的有效性，本文选取了灰度图像与彩色图像进行实验仿真，并与文献[13—17]中的算法进行对比，通过SF指标、SD指标、AG指标、QABF指标以及SSIM指标对融合后的图像进行评价。

为了使本文算法的有效性更有说服力，本文所有实验均在windows 10操作系统上的MATLAB 2013a环境下进行仿真。仿真实验过程中，滑动窗口大小设为8, NSST分解层数均设为3层。

3.1 灰度图像仿真结果与分析

实验选择了三组像素尺寸大小为256×256 , 颜色深度为8位灰度的图像作为源图像进行仿真，如图4-图6所示。其中，图4(a)-(b)分别为急性脑卒患者脑部的CT图以及MRI图；图5(a)-(b)则是多发性脑梗塞图MR-T1/MR-T2 ;图6(a)-(b)分别为正常脑部的CT图以及MRI图。

为了对比分析，本文选择了5组算法进行对比。其中图4-图6中的(c)图为应用李亦等[13]提出的香农熵加权稀疏表示算法进行融合，该算法将图像子带分为低频与低频、低频与高频、高频三部分进行自适应加权处理；图4-图6中的(d)图是利用陈轶鸣等[14]提出的算法进行处理，低频系数融合引入稀疏理论，通过空间频率激励脉冲耦合神经网络，根据点火次数来选择高频系数；图4-图6中的(e)图是采用王雷等[15]提出的平移不变剪切波变换的融合方法，该算法对低频系数融合采用区域系数绝对值和权重系数规则，高频子带则采用支持向量值激励的自生成神经网络的融合方法；图4-图6中的(f)图是利用殷明等[16]提出的非下采样四元数剪切波的融合算法，低频区域通过改进稀疏表示进行融合，高频领域结合改进空间频率，边缘能量和区域相似匹配度法进行处理；图4-图6中的(g)图是采用严春满等[17]提出的多聚焦图像融合算法，利用过完备稀疏表示理论对图像块进行稀疏分解，再经过显著性系数的融合，图像块的重构，图像块序列的重排得到最终的融合结果；图4-图6中的(h)图是利用本文提出的算法得到的融合图像。

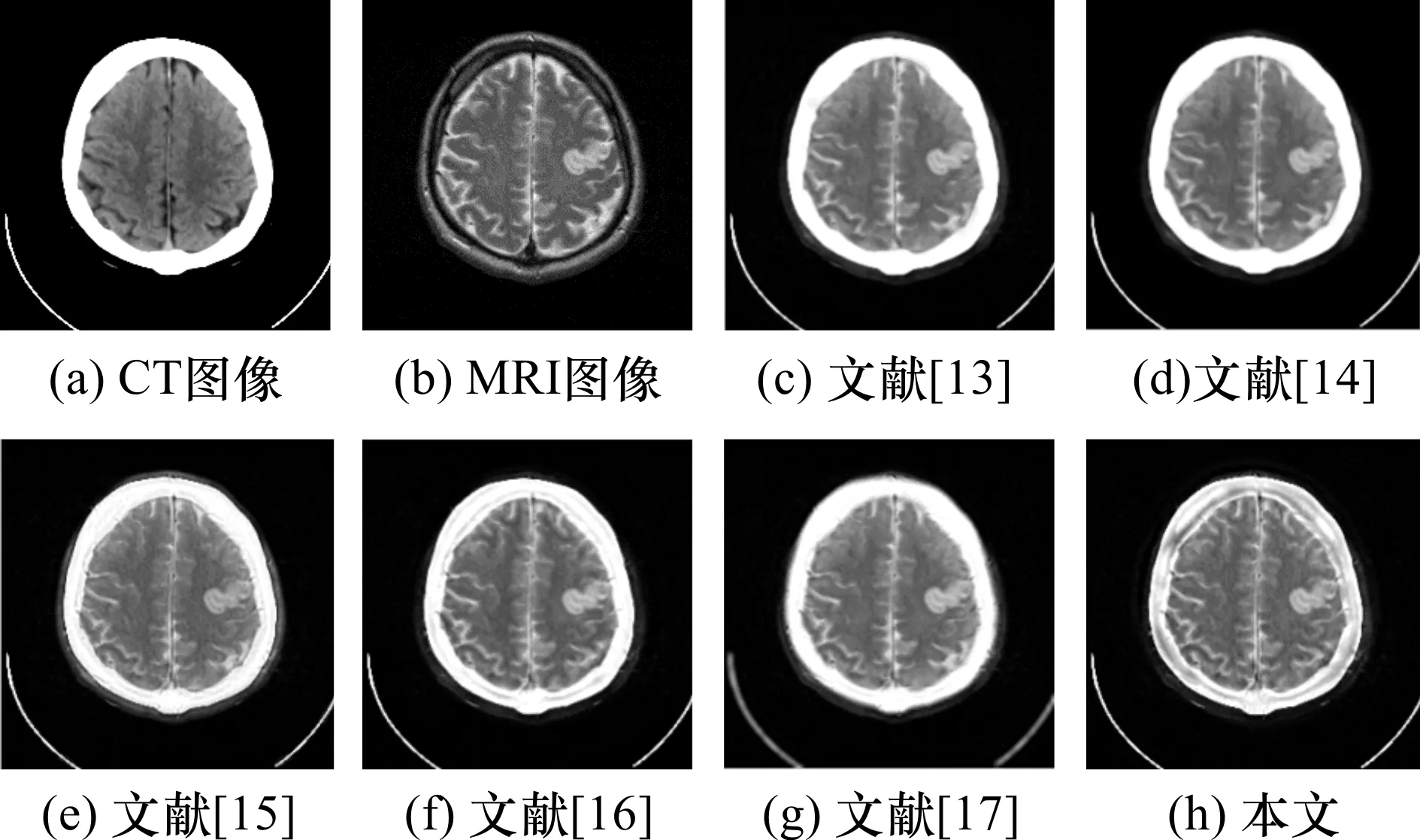
图4 急性脑卒脑部患者的CT/ MRI融合结果

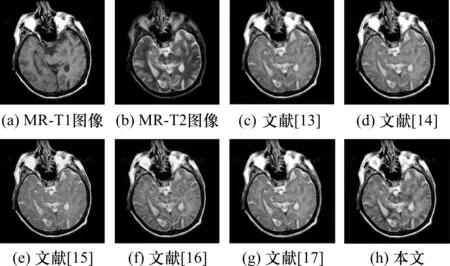
图5 多发性脑梗塞MR-T1/MR-T2融合结果

图6 正常脑部CT/MRI融合结果

从定性角度分析，观察图4-图6可以发现，本文算法得到的融合图像图4-图6中的(h)图在图像亮度，对比度，纹理边缘清晰度，视觉效果等方面均明显优于其它几幅图像，不仅使源图像的轮廓与纹理得到了有效保留，而且使图中的微小细节得到了呈现，对临床医学诊断与分析提供了强有力的支持。

观察图4不难看出，图4(c)-(e)以及图4(g)四幅图边缘纹理方面有些许模糊，微小细节没有得到有效展示，而图4(f)的纹理方面清晰度尚可，但中心区域亮度有些不足；观察图5 (c)-(d)两幅图亮度尚可，但纹理表现欠佳，而图5(e)-(g)图纹理尚可，然而对比度有所欠缺；图6中几幅图源图像的轮廓保留较好，但图6(c)-(d)图亮度不强，对比度不够理想，图6(e)-(g)图组织信息边缘有些许模糊，视觉效果有些不足。

从定量角度分析，本文选取了5种指标对融合后的图像进行分析，相关融合数据如表1-表3所示。

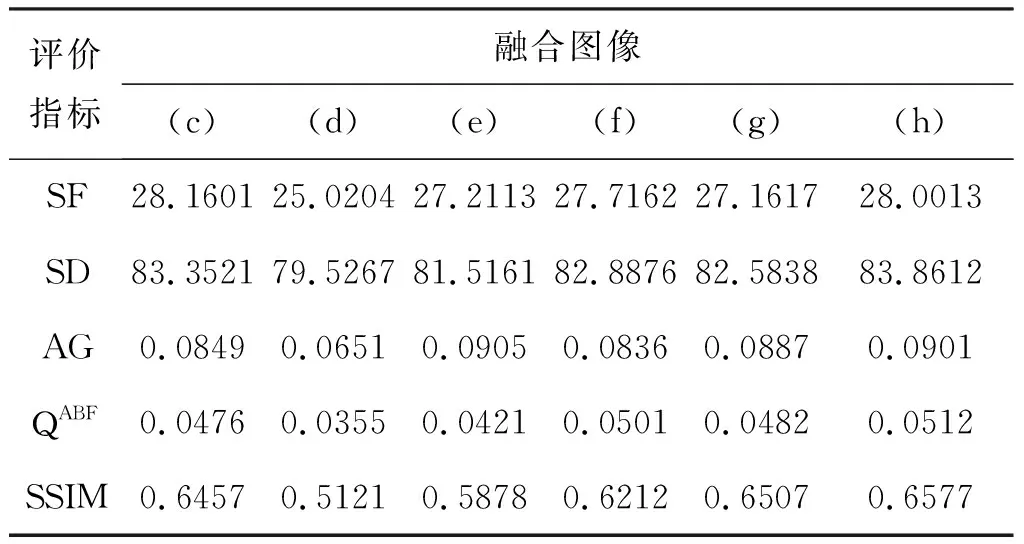
表1 图4中不同融合算法得到的相关融合指标

表2 图5中不同融合算法得到的相关融合指标

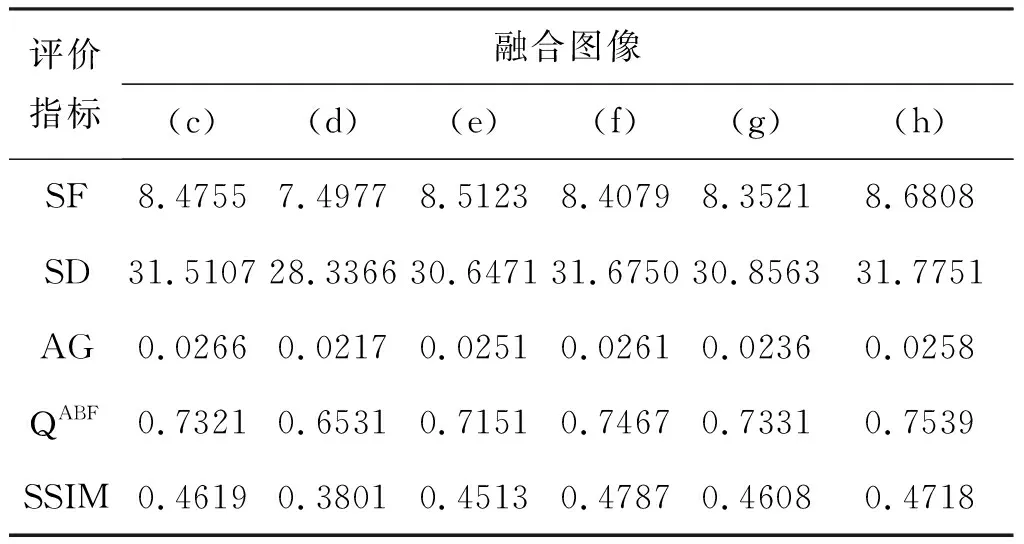
表3 图6中不同融合算法得到的相关融合指标

观察表1-表3可知，首先利用陈轶鸣等[13]算法得出的融合图像的评价指标普遍偏低，各项数值均不突出，这可能由于该算法精度不高所致，同时也说明此算法在图像融合领域有较大的局限性；其次，其它几种算法在进行图像处理时表现尚可，指标值相差不大，部分指标表现突出，比如表2中(g)图SD指标、表1中(c)图的SF指标、表3中(f)图的SSIM指标等更是达到最优，然而，几种算法中某些指标也略微偏低，如表1-表3中(e)图的SD指标值均偏低，这也说明此种算法得到的融合图像纹理模糊，在改善图像细节方面稍显不足；最后，观察各表中本文算法得到的融合图像指标值，表1-表3中通过本文算法得到指标值大都最优，此外，部分未达到最优值的指标与最高指标值相差较小，这充分说明了本文算法具有一定的优越性。

3.2 彩色图像仿真结果与分析

为了进一步验证本文算法的有效性，本文选取了两组彩色图像SPECT/MRI进行实验仿真。如图8(a)-(b)为医学领域转移性肺癌SPECT/MRI图像，而图9(a)-(b)为医学上正常脑部的SPECT/MRI图像。同上述灰度图像仿真一致，图8(c)-(h)以及图9(c)-(h)依次通过文献[13-17]中算法和本文提出的算法融合获得；此外，表4和表5分别为图8和图9中各算法得到的相关评价指标。

计算机上处理彩色图像通常采用RGB颜色系统，因此基于图像融合考虑，需要实现RGB系统与HIS系统之间的转换。此处在进行彩色图像融合处理时首先要将其从RGB系统映射到HIS系统；其次，提取其中的I(强度)分量与灰度图像进行融合；再次，将源彩色图像中H(色度)分量与S(饱和度)分量与上述融合结果结合；最后，进行HIS系统与RGB系统之间的转换即可得到融合后的彩色图像。融合框架如图7所示。

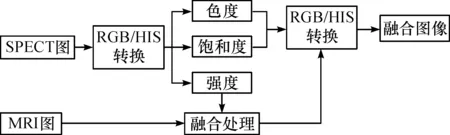
图7 彩色图像融合框架

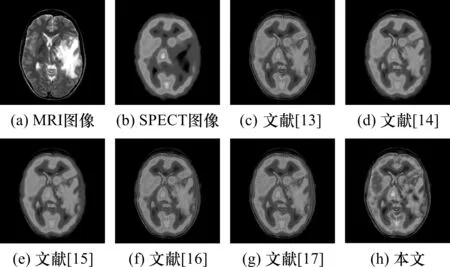
图8 转移性肺癌SPECT/MRI图像融合效果

图9 正常脑部SPECT/MRI图像融合效果

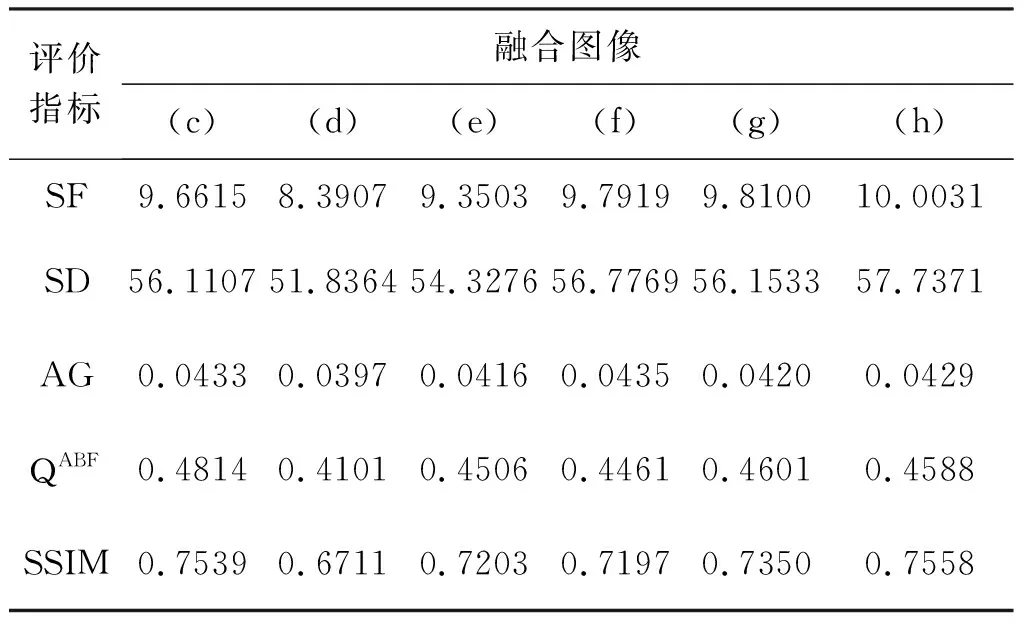
评价指标融合图像(c)(d)(e)(f)(g)(h)SF9.66158.39079.35039.79199.810010.0031SD56.110751.836454.327656.776956.153357.7371AG0.04330.03970.04160.04350.04200.0429QABF0.48140.41010.45060.44610.46010.4588SSIM0.75390.67110.72030.71970.73500.7558

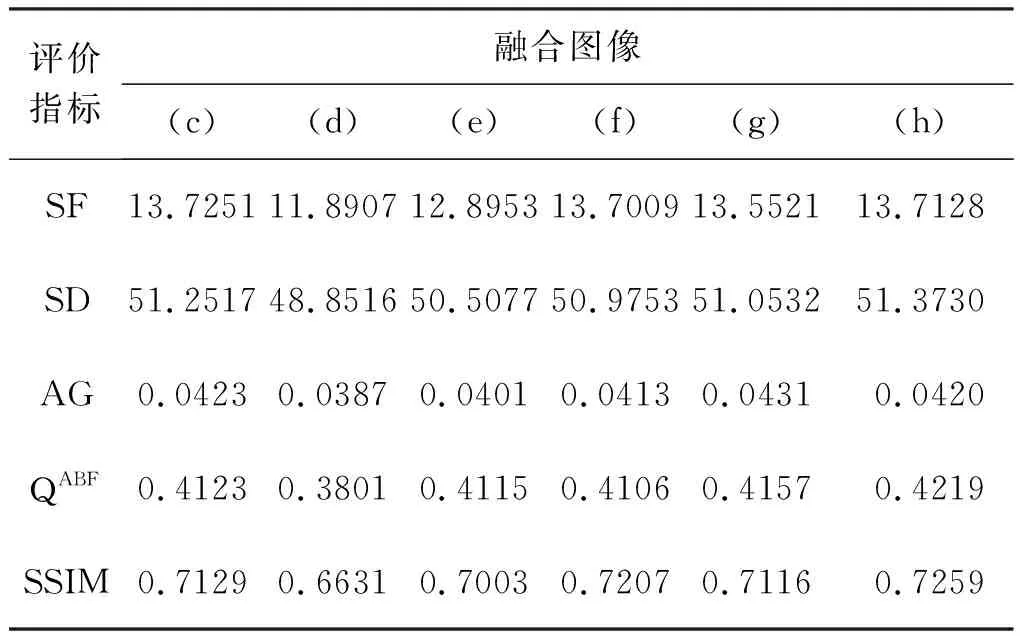
表5 图9中不同算法得到的相关融合指标

结合图8、图9不难发现，应用本文算法得到的融合结果图在图像亮度、纹理清晰度、局部对比度、视觉效果方面均优于其它图像，不仅保留了源图像的轮廓信息，而且凸显了重要的细节特征，对临床医学的诊断能够带来较大的便利。

从定性角度分析，图8(d)-(e)和图9 (d)-(e)融合效果图细节模糊，纹理不清，源图像的边缘带未尽可能的被保留，丢失了大量细节信息，不适用于医学诊断，同时也表明该算法在彩色图像领域应用有一定的缺陷；而图8 (c)和图8(f)-(g)三幅图以亮度尚可，但纹理仍不够清晰，而图9 (c)和图9(f)-(g)三幅图纹理清晰度有所改善，但图像亮度不佳，对比度不强，视觉效果有所欠缺，对医学诊断与治疗仍然不便；观察本文算法得到的彩色图像，纹理清晰，细节明了，视觉效果良好，主观上有力验证了本文算法的有效性。

从定量角度分析，观察表4-表5可以发现，陈轶鸣等[13]算法得到的融合指标全部偏低，指标值均不突出，融合效果较差；而其它指标值虽然相差不大，但某些指标值如表4中(e)的 SF指标略低，说明其信息丰富性不强，同理，表5中(f)的QABF指标值偏低，也表明其图像边缘存在一定的模糊；观察表4-表5中(h)图的指标值基本占优，即使未取得最优的指标值也接近最高，充分说明了本文算法表现良好，有一定的优越性，再次验证了本文算法的有效性。

4 结束语

图像融合技术的不断发展，极大地改善了人们的生活方式，也促使医学领域产生了巨大的变革。本文在研究非下采样剪切波技术的基础上提出了一种新的融合算法，即在低频领域采用引入稀疏理论对其进行融合处理，提高其稀疏度，而对于高频子带处理，本文采用相对标准差比较法进行融合，以提高其细节纹理的清晰度。仿真实验表明，本文算法得到的融合图像细节清晰，亮度适中，图像信息丰富，同相关算法比较，无论在主观视觉上还是客观指标上均具有一定的优越性。