Monotonicity and convexity properties of the generalized (p,q)-elliptic integrals

, ,

(School of Sciences, Zhejiang Sci-Tech University, Hangzhou 310018, China)

Abstract： In this paper, the authors obtain several monotonicity and convexity properties of the generalized (p,q)-elliptic integrals Kp,q(r) and Ep,q(r) for p,q∈(1,∞) and r∈(0,1), by studying the analytic properties of certain combinations in terms of Kp,q(r), Ep,q(r) and some elementary functions.

Key words： generalized (p,q)-trigonometric functions; generalized (p,q)-elliptic integrals; monotonicity; convexity

0 Introduction

Forr∈(0,1), Legendre’s complete elliptic integrals of the first and second kinds are defined as

respectively, which are the special cases of the Gaussian hypergeometric functions

(1)

where (a,0)=1 fora≠0, and (a,n) is the shifted factorial function

(a,n)=a(a+1)(a+2)…(a+n-1)

(2)

forn∈N={k|kis a positive integer}. (See [1])

In recent years, certain generalizations of the classical trigonometric functions have attracted much interest. Forp,q∈(1,∞) and forx∈[0,1], define the function

(3)

and set

(4)

whereBis the classical beta function. The function arcsinp,qxhas an inverse defined on [0,πp,q/2], which can be extended to an odd 2πp,q-periodic function, denoted by sinp,q, on the setRof real numbers by natural procedures designed to mimic the behaviour of the sine function. The function sinp,qis said to be the generalized (p,q)-sine function, reduces to the classical sine function whenp=q=2, and occurs as an eigenfunction of the Dirichlet problem for the (p,q)-Laplacian. (Cf. [2-3].)

Forp,q∈(1,∞) and forr∈(0,1), the so-called generalized (p,q)-elliptic integrals of the first and second kinds are defined as

(5)

and

(6)

respectively, which were introduced and studied recently. (Cf. [4-5].) Forp=q=2, these two functions reduce to the complete elliptic integrals K(r) and E(r), respectively. It is easy to see that the generalized (p,q)-elliptic integrals have the following expressions (cf. [5]).

(7)

and

(8)

Here and hereafter, we letr′=(1-rq)1/q. Clearly, Kp,q(Ep,q) is strictly increasing (decreasing, respectively) on (0, 1). By [4, Corollary 1.2], these two functions satisfy the Legendre relation

It is well known that the complete elliptic integrals K and E have many applications in several fields of mathematics as well as in physics and engineering. Numerous properties have been obtained for K and E(cf., for instance, [6-10]). However, only a few basic properties of the generalized (p,q)-elliptic integrals Kp,qand Ep,qhave been revealed (see [4-5, 11]). It is natural to ask whether the known properties of Kand E can been extended to Kp,qand Ep,q.

The purpose of this paper is to present several monotonicity and convexity properties of Kp,qand Ep,q, by studying the analytic properties of certain combinations defined in terms of Kp,q,Ep,qand some elementary functions, thus extending some known properties of K and E to Kp,qand Ep,q.

Throughout this paper, we always leta=1-1/pandb=a+1/qforp,q∈(1,∞),γ=0.577215… be the Euler constant,ψthe classical psi function, and let

R(x,y)=-2γ-ψ(x)-ψ(y)(x,y∈(0,∞))

(9)

1 Main Results

In this section, we state the main results of this paper.

Theorem1Forp,q∈(1,∞), we have the following conclusions:

a) The functionf1(r)≡(Ep,q-r′qKp,q)/rqis strictly increasing and convex from (0, 1) onto (aπp,q/(2b),1).

b) The functionf2(r)≡r′qKp,q/Ep,qis strictly decreasing from (0, 1) onto itself.

c) The functionf3(r)≡(Ep,q-r′qKp,q)/(rqKp,q) is strictly decreasing from (0, 1) onto (0,a/b).

d) The functionf4(r)≡(Kp,q-Ep,q)/(rqKp,q) is strictly increasing from (0, 1) onto (1/(qb),1).

e) The functionf5(r)≡(Ep,q-r′qKp,q)/(Kp,q-Ep,q) is strictly decreasing from (0, 1) onto (0,aq).

f) The functionf6(r)≡r′q(Kp,q-Ep,q)/(rqEp,q) is strictly decreasing from (0, 1) onto (0,1/(qb)).

Theorem2Forp,q∈(1,∞) andc∈(-∞,∞), we have the following conclusions:

a) The functiong1(r)≡r′cKp,qis decreasing (increasing) on (0, 1) if and only ifc≥a/b(c≤0, respectively) withg1((0,1))=(0,πp,q/2) ifc≥a/b.

b) The functiong2(r)≡r′cEp,qis increasing (decreasing) on (0, 1) if and only ifc≤-1/(pb)(c≥0, respectively), withg2(0,1)=(πp,q/2,∞) ifc≤-1/(pb).

Theorem3Forp,q∈(1,∞) andc∈(-∞,∞), the functionh1(r)≡Kp,q+clogr′ is increasing and convex (decreasing) on [0, 1) if and only ifc≤aπp,q/(2b)(c≥1,respectively). Moreover, ifc≥1, thenh1is concave on [0, 1). In particular, the functionh2(r)≡Kp,q+logr′is strictly decreasing and concave from (0, 1) onto (R(a,1/q)/q,πp,q/2), so that forp,q∈(1,∞) andr∈(0,1) andR=R(a,1/q)/q,

(10)

with equality in each instance if and only ifr=0.

Remarka) Ifp=q=2, then Theorem 1 a) and e), and Theorem 1 c)—d) reduce to [6,Theorem 3.21(1) & (6)] and [6, Exercise 3.43 (46) & (32)], respectively, while Theorems 2—3 reduce to [6,Theorem 3.21(7) & (8)] and [6, Theorem 3.21(3)], respectively.

b) Ifp=qanda=1/p, then Theorems 1—3 give several properties of the generalized elliptic integrals Kaand Ea, which were obtained in [12, Lemmas 5.2 & 5.4, Theorem 5.5(1)].

We now recall the following two lemmas needed in the proofs of our main results.

Lemma1([13]) Letrn,sn∈(-∞,∞) forn∈N. Suppose that the power series

(11)

are both convergent for |x|<1. If allsn>0 and ifrn/snis strictly increasing (decreasing) inn∈N, then the functionR/Sis strictly increasing (decreasing, respectively) on (0, 1).

Lemma2([5]) Forp,q∈(1,∞) andr∈(0,1),

(12)

2 Proofs of Main Results

2.1 Proof of Theorem 1

a) By (1) and (7)—(8), we have

(13)

wherebn=an/(n+b) andan=(a,n)(1/q,n)/[(b,n)n!], and hence the monotonicity off1follows. Clearly,f1(1-) =1. By (13),f1(0+)=aπp,q/(2b).

b) Observe that Ep,q-r′qKp,qis increasing on (0,1) by (13), and Ep,qis decreasing on (0, 1). Sincef2(r)=1-(Ep,q-r′qKp,q)/p,q, the monotonicity off2follows. The limiting values off2are clear.

c) It follows from (1), (7) and (13) that

(14)

Sincebn/an=1/(n+b) is strictly decreasing inn∈N∪{0}, we obtain the monotonicity off3by Lemma 1.

The limiting values off3are clear.

d) Sincef4(r)=1-f3(r), part d) follows from part c).

e) Part e) follows from parts c)—d).

f) Clearly,f6(r)=1-f1(r)/Ep,q, and hence part f) follows from part a). □

2.2 Proof of Theorem 2

a) Letf3be as in Theorem 1 c). Then by Lemma 2 and by differentiation,

Hence by Theorem 1 c), g1is decreasing (increasing) on (0, 1) if and only if

b) Letf6be as in Theorem 1 f). Then by Lemma 2, we have

Hence by Theorem 1 f),g2is increasing (decreasing) on (0, 1) if and only if

yielding the result in part b) as desired. □

2.3 Proof of Theorem 3

Letf1be as in Theorem 1 a). Then Lemma 2 and differentiation give

so that by Theorem 1 a),

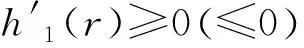
which yields the monotonicity ofh1.

Next, it follows from (1) and (7) that

(15)

whereAn=qπp,q(a,n)(1/q,n)/[2(b,n)(n-1)!]. Since

The limiting valueh2(0)=πp,q/2, and the monotonicity and concavity properties ofh2are clear. By [1,15.3.10], we obtain the limiting valueh2(1-)=R(a,1/q)/q.

The double inequality and its equality case are clear. □