A double inequality for the ratio of complete elliptic integrals of the first kind
2018-11-07,,
, ,
(School of Sciences, Zhejiang Sci-Tech University, Hangzhou 310018, China)
Abstract: In this paper, the authors present a double inequality for the ratio of complete elliptic integrals of the first kind, in which the upper bound is much better than those known to us, while the proof of the lower bound is much simpler than that recently given by Alzer and Richards.
Key words: complete elliptic integral; monotonicity; lower and upper bound; inequality
0 Introduction

(1)
and
(2)
respectively, with K(0)=E(0)=π/2,K(1-)=∞ and E(1)=1. The basic properties of K and E are collected, for instance, in [1]589-592and [2-4]. It is well known that these special functions have many important applications in mathematics, physics and engineering. In particular, they play an important role in quasiconformal theory.
During the past decades, many authors have obtained various properties for K and E, including functional inequalities (cf. [5-14]). In [5, Theorem 3.11], for example, the following double inequality was obtained
(3)

(4)



c) For allr∈[0,1),
(5)
with equality in each instance if and only ifr=0. Moreover, the coefficient 1/5 in the second inequality in (5) is the best possible.
1 Preliminaries
In this section, we prove two technical lemmas needed in the proofs of our main results stated in last section. In the sequel, we always letNbe the set of natural numbers, put
forn∈N∪{0}, where Γ(x) is the classical gamma function[1]255-258, and forn∈N, let
(6)
Clearly,a0=π,a1=π/4 anda2=9π/64.

16/9≤an/a2n≤2
(7)

yielding the monotonicity of {bn}.

Lemma2Forn∈N,
0 (8) Proof. By (6),A2n+2>0 if and only if (9) It is easy to verify that forn∈N, (10) By (7) and (10), we have which is greater than 1 since Hence the first inequality in (8) follows from (9). Next, by (6), we can easily see thatA2n+2 (11) It is easy to show that (12) Forn∈N, letP3(n)=5+5[(2n+1)/(n+1)]2and Then it follows from (10)-(12) and (7) that and hence,P2(n)<1 for alln∈Nif P5(n)≡P4(n)-2P3(n)>0,n∈N (13) By computation, we have 16(4n-3)2(4n-1)2(2n+1)2(n+1)2P5(n) =221184n7-97280n6-93184n5+43648n4-33792n3+15536n2+7392n-1179 =1024n5(216n2-95n-91)+1408n3(31n-24)+15536n2+(7392n-1179)>0 forn∈N. Hence (13) really holds, so thatA2n+2 c) The first inequality and its equality case in (5) follows from part a) or part b). (Note that this result has been proved in [7] by using a quite complicated method.) by whichh(r) has the following power series expansion (14) SinceA2n+1-rA2n+2>A2n+1-A2n+2>0 forr∈[0,1) andn∈Nby Lemma 2, it follows from (14) and Lemma 2 that (15) with equality in each instance if and only ifr=0. This yields the second inequality in (5) and its equality case. It is well known that (16) asr→1[1]559. Forr∈[0,1), let i) For allr∈[0,1), it is clear thatF2(r)>1 and which shows thatF1(r)<1 ii) One can verify thatF1(r) r-2[625(4+r)4(1+r)(1-r2)][F3(r)4-F1(r)4]=r13+17r12+111r11+415r10+1440r9+4624r8+9808r7+21664r6+46240r5+43680r4+102400r3+58225r2+10000r+92000>0. Hence the upper bound given in (5) is better than the second upper bound given in (3). b) From (15) and Lemma 2, we see that forr∈[0,1), (17) c) It can be proved that Theorem 1 can be extended to the generalized elliptic integrals Ka(r)≡(π/2)F(a,1-a;1;r2) fora∈[0,1)andr∈[0,1),although the proof of this extension is more difficult than that of Theorem 1. However, Theorem 1 can not be extended to the zero-balanced hypergeometric functionsF(a,b;a+b;x) for some values ofa∈(0,∞) andb∈(0,∞). These results will be given in a separate paper. d) Our computation supports the validity of the following conjecture: There exists a unique numberr0=0.70679…, such that the function (18) forr∈[0,1), with equality in each instance if and only ifr=0, and the coefficientscand 1/5 in (18) are both the best possible, thus improving the first inequality in (5).

2 Proof of Theorem 1


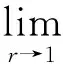
3 Concluding Remarks




