编织角对三维编织复合材料弯曲性能的影响

2018-11-07，，

浙江理工大学学报(自然科学版) 2018年6期

，，

(浙江理工大学机械与自动控制学院，杭州 310018)

0 引言

三维编织复合材料是利用编织技术将纤维织成三维整体织物，再与基体(树脂、金属等)复合的纺织结构材料，与层合复合材料相比，它克服了层间强度低、受力后易分层的缺点，因其比强度高、力学性能优良等优点，被广泛应用于航空、航天、军事领域及民用领域[1-4]。

近年来，国内外众多学者对于三维编织复合材料力学性能进行了研究，曹海建等[5-6]研究了编织结构、编织角度等结构参数对玻璃纤维/树脂复合材料管件弯曲性能及轴向压缩性能的影响规律。马少华等[7]认为湿热环境对碳纤维环氧树脂复合材料弯曲强度的影响大于弯曲模量的影响，干态试样发生脆性断裂，湿态试样只有在高温下才发生断裂。Joseph等[8]研究了短剑麻纤维/低密度聚乙烯复合材料的力学性能。孙颖等[9]研究了碳/芳纶混编三维编织复合材料拉伸性能，发现同种编织结构下，碳/芳纶混编复合材料的各项性能明显优于单一复合材料。上述这些复合材料的成分大部分是不完全降解的，废弃物处理中会给环境带来污染。随着人们环保意识的增强，越来越多的人开始致力于研究用天然植物纤维与可完全降解树脂结合制成的可降解复合材料，例如麻纤维增强聚乳酸复合材料[10]。

本文中复合材料使用的纤维是天然植物纤维亚麻，使用的树脂是可降解聚乳酸(PLA)，先用三维绘图软件SolidWorks构造三维编织亚麻材料模型，采用有限元模拟软件ABAQUS对模型进行网格划分及静力学弯曲性能模拟，通过载荷-位移数据计算模型弯曲应力-位移数据，分析出不同编织角度对复合材料的弯曲性能及各材料的应力分布，结合实验结果，对编织结构的优化提出建议。

1 有限元仿真

1.1 工作原理

有限元分析是利用数学近似的方法对真实物理系统(几何和载荷工况)进行模拟，其基本原则是保证计算结果正确性和控制模型计算规模。有限元分析工作原理是：首先对复合材料模型进行基本设定，旨在减少计算量，再根据复合材料的几何特征建立几何模型，并对材料各成分赋予材料属性，最后根据实验加载方式设置合理的边界条件和加载设定。

1.2 基本设定

为了简化模型并减少数值模拟中的计算量，参照文献[11-12]，本文在建立复合材料结构模型时进行了以下设定：

a) 实验中将编织好的纤维绳子压扁后再与树脂复合，所以三维建模将纤维截面设置成椭圆形(如图1所示)，且纤维截面沿长度方向保持不变，纤维为横观各项同性材料。

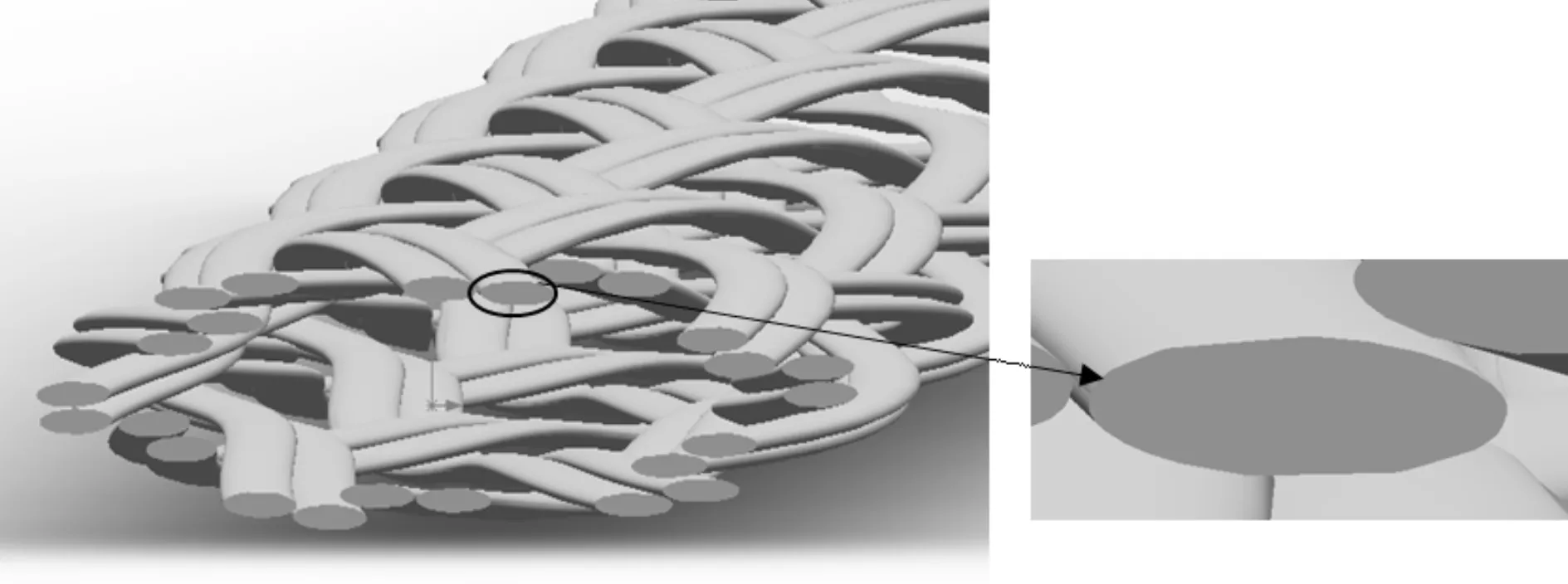
图1 纤维模型示意(右图为局部放大图)

b)纤维束模型是建立有限元全尺寸细观结构的基础，预成型体固化形成复合材料后，树脂会浸润到纤维束间，因此，假设纤维束是含有亚麻纤维束和树脂的单向板，如图2所示。

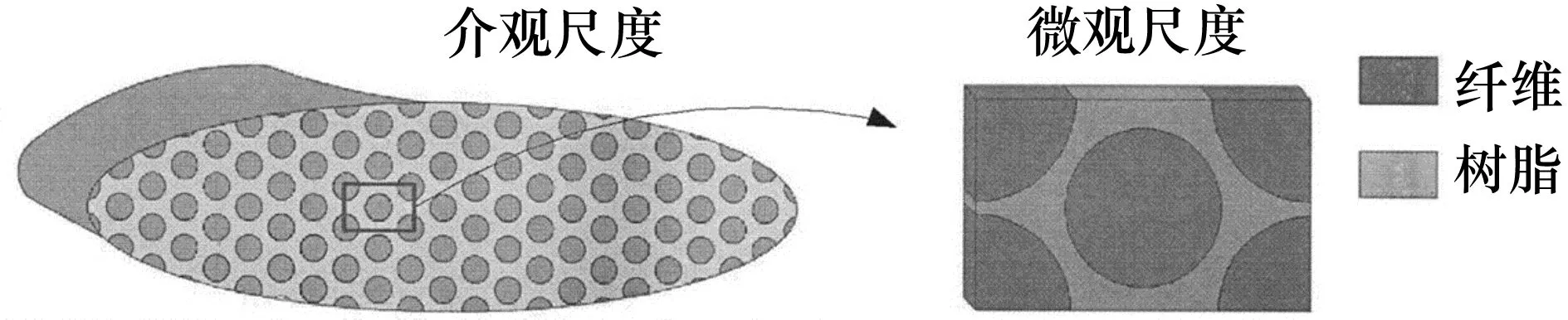
图2 纤维束模型

c) 复合过程是理想条件下进行的，纤维和树脂界面性能良好。树脂中没有裂痕、缺陷和气泡等会产生应力集中点的位置。

d) 碳纤维和树脂基体界面为理想粘结状态。

e) 板件与压头或托头之间光滑接触，无摩擦。

1.3 构建有限元模型

本次仿真实验建立了三种模型，编织角度分别是35°、45°、55°，下面以55°为例介绍模型的构建。

首先用软件SolidWorks建立亚麻编织模型，如图3所示。通过切除功能建立符合材料中树脂基体的结构模型，建立三点弯曲测试压头的结构模型，并将ABAQUS界面中组装纤维束、树脂基体及试验测试压头的结构模型，如图4所示。

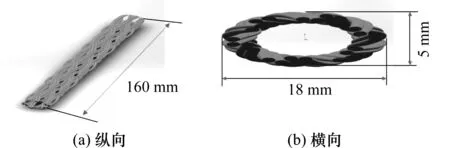
图3 亚麻纤维几何模型

图4 复合材料及压头结构模型

在ABAQUS中设置复合材料纤维束、树脂基体的力学性能参数，如表1所示。

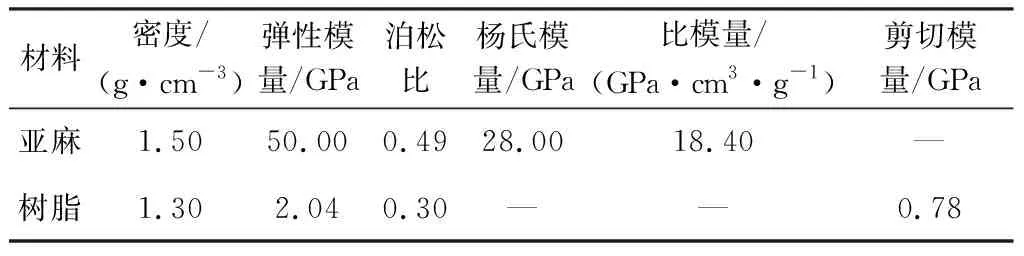
表1 材料的属性

使用ABAQUS网格划分功能中四面体网格对复合材料及压头进行网格划分，旨在保证模拟精度前提下提高计算机计算效率。划分网格后的模型如图5所示，其中纤维采用的是具有最高计算精度的C3D8R实体单元，因为纤维截面形状规则、运动轨迹规律。树脂是填充进纤维束间，故内部结构较复杂，采用的是C3D4实体单元，压头和托头的网格类型与编织纱相同，假定与试件光滑接触，其中编织角为35°、45°和55°三维编织复合材料模型的总网格数量分别为503754、873620、1217309。实际结构中，树脂和纤维之间存在摩擦，由于摩擦系数未知，分析中假定加载过程中两者不发生滑移，故采用绑定约束，树脂为“主动面”，纤维为“从动面”，纱线之间定义为“自接触”。根据实验测试情况设置边界条件，Y、Z方向完全固定，对X方向设置15 mm的位移，提交计算。

图5 划分网格后的复合材料结构模型

2 实验

2.1 复合材料制备

2.1.1 材料

纤维：亚麻纤维，湖州练市明通麻纺厂；树脂：聚乳酸，浙江海正生物材料股份有限公司，保持干燥，闲置期限不超过三个月。

2.1.2 三维编织复合材料的制备工艺

a) 编织物的预处理：用环形编织机将24根半径为1 mm的亚麻纤维编织在芯轴上，通过改变编织机的卷曲速度和环形速度编织出具有不同编织角度的纤维试样。

b) 复合成型：将预先织成的三维织物裁剪成500 mm长度，浸渍树脂胶液，抽出芯轴，在Y/TD71-45A塑料制品液压机上进行模压。

c) 复合材料的制备：自然冷却，待树脂固化以后，将试样切割成160 mm，即得三维板状编织复合材料。

材料制备参数如表2所示，实验过程示意如图6所示。

表2 材料制备参数

图6 实验过程示意

2.2 测试标准

本次三点压弯实验的参考标准为GB/T 3356-2014《定向纤维增强聚合物基复合材料弯曲性能试验方法》，选择工作极限为100 KN的万能试验机，压缩速度为2 mm/min，压缩位移为15 mm。示意如图7所示，其中压头/托头直径D=φ10 mm，板件高度H=5 mm，两托头中心距L1=100 mm，板件长度L2=160 mm，压头/托头长度L3=70 mm，板件宽度B=18 mm。

图7 三点压弯示意

3 三点弯曲结果分析

3.1 有限元模拟结果分析

在复合材料的三点弯曲试验中，一般只能得到最终的抗弯力-位移曲线，直接观察弯曲过程纤维和树脂的变形及其与应力分布的相互作用是很困难的，而有限元模拟则可以解决这一问题，清晰直观展现材料弯曲过程中应力分布及应力传播方式。

以编织角为55°的仿真分析为例介绍复合材料的仿真结果，材料弯曲过程等效应力变化云图如图8所示。由图8可知，当压头匀速向下移动时，与压头接触部分的材料开始弯曲受力，随着压头继续下移，材料上应力开始以压头为中心向两端开始扩散，材料受力增加，发生空间弯曲变形，最大应力分布在与压头接触的位置，即中间段，最小应力值分布在两边托头位置处。纤维和树脂特征点的等效应力(米塞斯应力)-时间曲线如图9所示，纤维所受的最大应力为20.96 MPa，树脂所受最大应力为10.17 MPa，当模拟的等效应力强度达到结构材料的极限强度时，认为材料被破坏，并且应力不再增加。

将有限元分析中抗弯力的数据导出，通过公式计算出弯曲应力，绘出如图10所示的弯曲应力-位移曲线。结合图8和图9可知，在三点压弯的前期，曲线处于线性阶段，应力较小，模型开始弯曲，应力集中不明显，当弯曲应力达到最大值时，由于树脂的应变率比纤维低，发生相同形变时，两者的粘连层发生破坏，树脂开始剥离，在应力达到峰值后，由于纤维与树脂分离，失去固化作用的纤维体表现为柔性，且纤维的拉伸模量较大，因此曲线趋于平缓，通过数值仿真结果中所反映的应力情况，说明了在树脂与纤维分离之前复合材料结构件中纤维承受了主要的外载荷力，而树脂在该过程中主要作用是把纤维粘接成为整体，使之能起协同作用，并保护纤维不受腐蚀和机械损伤，并且传递应力。

经典层合板理论是基于基尔霍夫-勒夫(Kirchhoff-Love)假设即直线法假设和法线长度保持不变、z向应力可以忽略假设建立的薄层合板中面变形方程，其缺点是只能计算面内应力，而基于有限元分析方法建立的三维编织复合材料结构模型，能得到材料内部结构的应力分布，对复合材料的性能强度分析及预测具有重要的理论意义和实用价值。

图8 编织角为55°的材料弯曲过程与等效应力变化云图

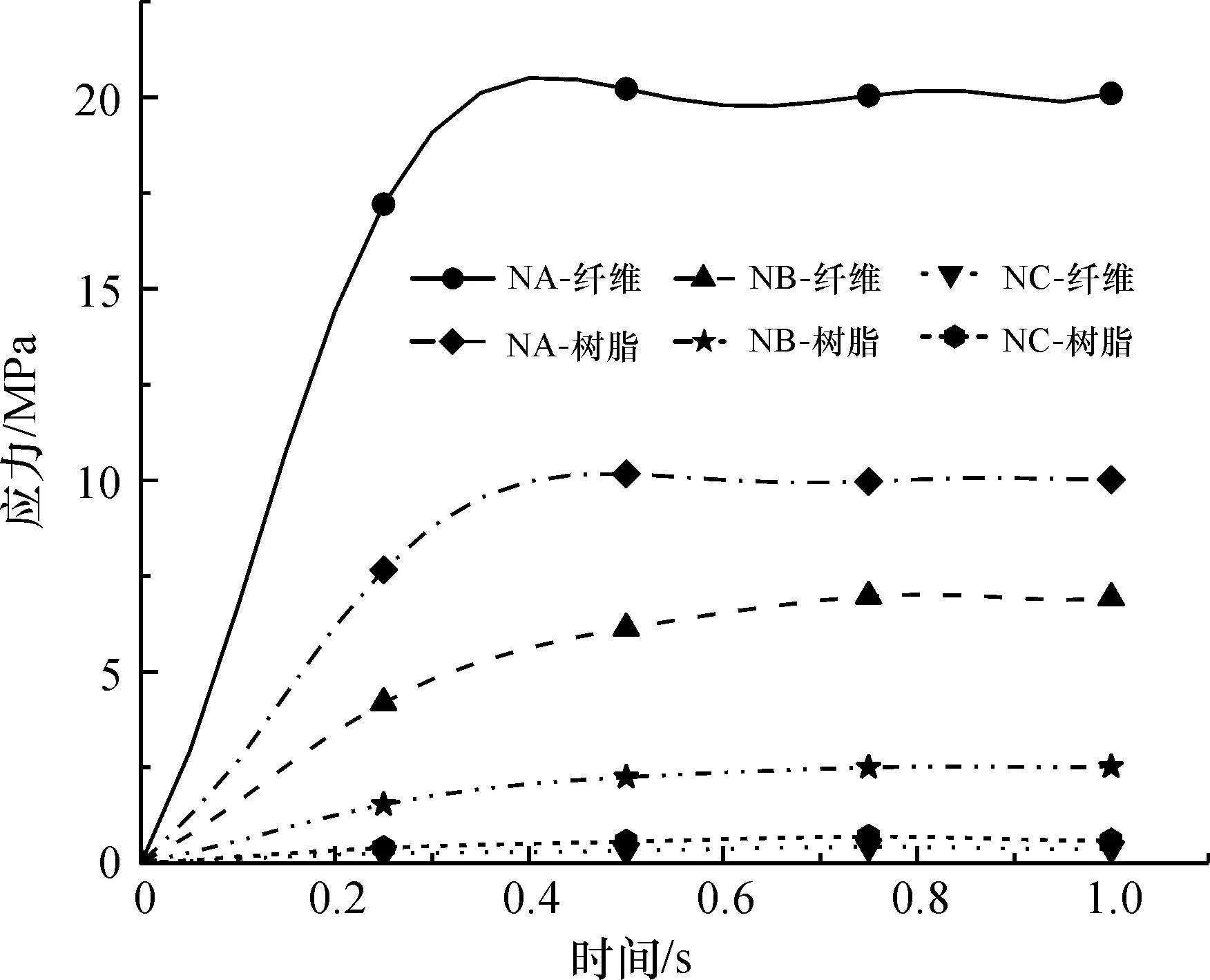
图9 编织角为55°的树脂和纤维特征点的等效应力-时间曲线

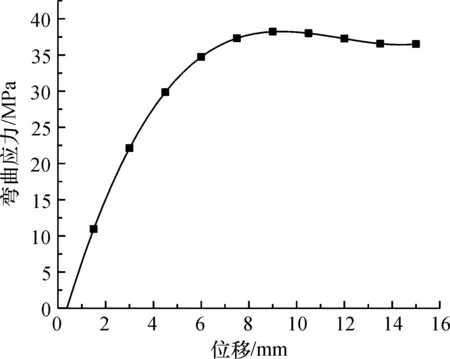
图10 编织角为55°的材料弯曲应力-位移曲线

3.2 模拟结果与实验对比分析

图11为编织角55°材料的实验和仿真结果不同视野的对比，其中仿真结果将纤维和树脂的结果分开显示。将数值模拟的各个角度分析数据提取，并用公式计算出弯曲强度(最大弯曲应力)、达到弯曲强度产生的应变以及弯曲模量，与实验结果进行对比，如图12和表3所示。表3中σM为弯曲强度，εM为达到弯曲强度的应变，E为弯曲模量。

图11 编织角为55°材料的实验与仿真结果对比

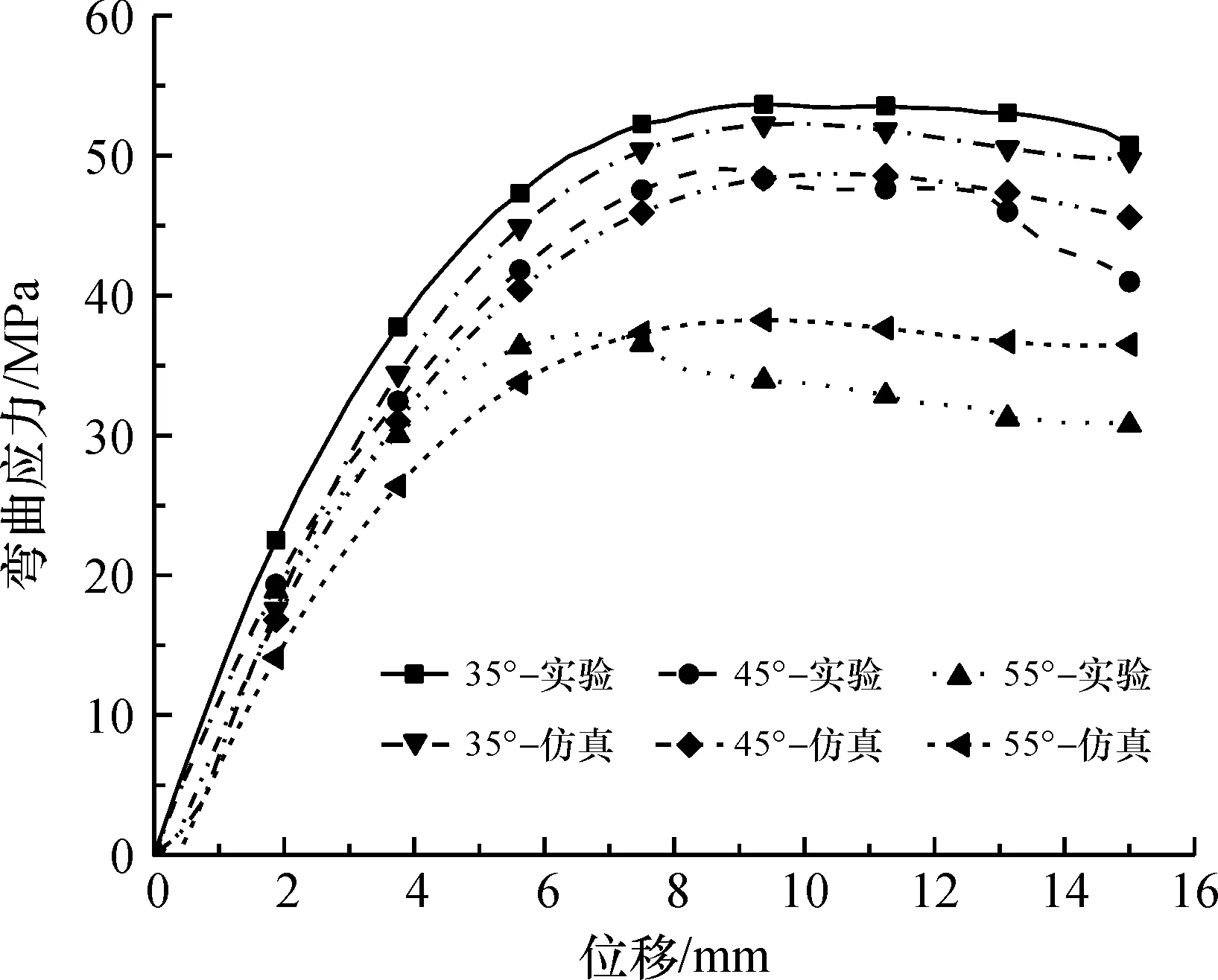
图12 不同编织角的材料弯曲应力-位移曲线

角度/(°)参数σM/MPa仿真实验σM相对误差标准差/%E/ MPa仿真实验εM仿真实验3552.2753.677.93948.77970.140.050.054548.6949.117.35891.06882.380.050.065538.2537.2815.94691.28653.910.050.06

由图12和表3可知，有限元模拟结果无论从曲线趋势还是从弯曲应力，都与实验结果接近。数值模拟是在理想条件下计算的，因此，模拟曲线比实验曲线更加平滑。从整体来看，各个角度的曲线都是先呈线性上升达到最大值，然后曲线趋于平缓或略微下降，达到弯曲强度的应变，仿真与实验结果都接近于0.05。

在表3中，编织角为35°的复合材料的弯曲强度和弯曲模量是三种情况中最大的，编织角为 55°的材料强度和模量都是最小的。而45°、55°编织角的材料在三点压弯后期弯曲应力出现较明显的下降。图13为不同编织角复合材料纤维应力集中区域特征点的应力-时间曲线，由图可知三种情况纤维所受最大应力值较一致，试验过程表明纤维应力均达到极限值。随着试件的损伤，材料特征点的等效应力都会出现一个跌落，弯曲强度越大，等效应力跌落出现的越晚，曲线越平缓。这是由于材料的强度较低时，基体的应力很难传递到纤维上，纤维不能起到承载作用，而基体的模量低，使得材料在较小载荷作用下就开始出现损伤；当材料的强度较高时，纤维能起到较好的承载作用，因此材料能承受较大的载荷。

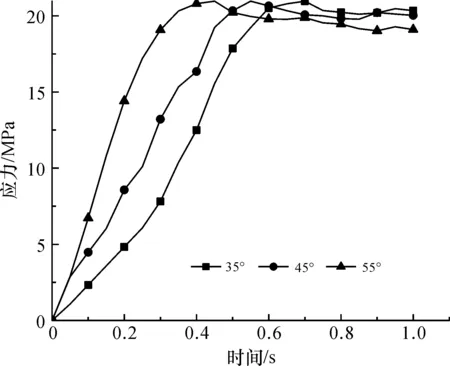
图13 不同编织角的复合材料应力-时间曲线(应力集中处特征点-NA)

在实验中，试件的破坏模式大都是管件顶面树脂剥落，极少数出现底部树脂拉伸断裂。而增强体纤维未出现明显的破坏。三种试件的破坏样貌如图14(a)所示，白色区域为树脂剥落样貌，图14(b)是数值模拟的结果。不同编织角度的材料，其树脂剥落面积也存在差异，图中可以看出，35°的材料面积最大，其次是45°，55°的材料面积最小。相同长度情况下，较大编织角的纤维体积含量较高，因此在压弯过程中，更多的纤维参与受力拉伸，由于纤维的增强体特性，树脂剥落面积会随编织角度增大而减小。仿真结果与实验大致吻合。

本文中借助ABAQUS有限元模拟软件得到的材料应力分布以及材料弯曲应力-位移曲线与实验结果具有较好的一致性，说明所建立的三维复合材料的有限元模型正确有效，借助有限元分析软件对复合材料力学性能进行预测与分析，比较经济有效。