波浪荷载作用下频率对饱和珊瑚砂动力特性影响研究
2018-11-06李晶鑫方祥位申春妮
李晶鑫,方祥位,2,申春妮,李 腾
(1.陆军勤务学院 军事设施系, 重庆 401311; 2.重庆大学 土木工程学院, 重庆 400044; 3.重庆科技学院 建筑工程学院, 重庆 401331)
珊瑚砂在海洋环境中,不仅自身不可避免的受到周期性荷载的影响,如风、浪等周期荷载和可能发生的地震作用、暴风荷载。在建设各种设施和建筑时,还遭受了其传导的动态载荷的影响以及施工过程中的周期荷载的影响。故下部珊瑚砂地基处于复杂的应力状态[1]环境中,通常为风、波浪、车辆荷载及其他动力荷载及静力荷载共同作用,一般表现为动荷载能量累积量远大于静荷载能量累积量。在波浪循环动荷载作用下,动主应力轴连续旋转,其应力路径为一个圆。在珊瑚砂海域工程问题频发且相关研究结果指出,主应力轴连续旋转对土体的强度及变形特性有显著影响。早在1965年Broms等[2]就已对黏土采用不排水扭剪试验,得出主应力轴方向的连续旋转会使粘土孔隙水压力增大。Symes等[3]的研究也表明,主应力轴方向角连续变换会加速孔隙水压力累积,初始主应力方向同样会产生孔隙水压力增长速度及模式的差异。Ishihara等[4]和Towhata[5]等采用HCA扭剪仪对日本标准砂进行了普通动三轴、循环扭剪和模拟主应力轴连续旋转的扭剪试验。试验结果得出以下结论:在纯主应力轴旋转路径下同样会产生孔隙水压力的累积;在相同的试样密实度和循动剪切应力条件下,HCA扭剪试验较传统动三轴所得动强度低30%。Dakoulas等[6]的研究进一步验证了纯主应力轴旋转对砂土的孔隙水压力和变形特性都有影响。沈瑞福等[7]利用一台美制双向振动动力扭剪仪对同一砂样的重复试验表明:考虑主应力轴方向旋转的土体强度比循环扭剪低30%左右。郭萤等[8]利用大连理工与日本联合设计、研制的空心圆柱扭剪仪对福建标准砂进行了双向耦合剪切试验与循环扭剪试验。试验结果同样表明,在相同的试样密实度和循动剪切应力条件下,HCA扭剪试验较传统动三轴所得动强度低,且降低幅度在10%~30%之间。Georgiannou V N等[9]对饱和砂土进行不排水循环三轴扭剪耦合试验,发现偏应力大小、相对密度和中主应力系数b是导致孔隙水压力上升使试样弱化的重要因素。
世界上大部分的珊瑚礁都位于南北回归线内的热带海域。中国大部分的珊瑚岛礁位于北回归线以南的热带海岸和海洋中。南海填海造岛工程主要采用珊瑚砂(钙质砂),热带海洋环境中的珊瑚砂,是一种特殊类型的岩石和土壤介质,珊瑚碎屑与其他海洋生物碎屑是其主要成分,珊瑚砂碳酸钙含量非常高,通常被称为珊瑚砂和钙质砂[10-16]。特殊的结构、材料组成和发展环境使珊瑚砂具有特殊的工程力学性能。Datta[17]等选取以印度西侧海域为生长环境的珊瑚砂,进行不排水循环压缩试验,之后观察到其孔压比、循环振动频次对数呈直线关系,当在较低循环荷载作用下时,珊瑚砂依旧无法避免出现明显塑性变形。Morrisno等[18]样本取于南非近海位置,在相同位置下取得两类珊瑚砂,其区别在于CaCO3含量不同。而后他采取体积、应力条件一致的循环直剪试验,以及循环空心圆柱扭剪试验,观察到这一比重差异可影响珊瑚砂动力学性质,当体积不变时,CaCO3含量较高,剪应力弱化现象较明显,而反之则不会有明显弱化表现;当应力水平一致时,对应的弱化迹象没有体积水平一致时的弱化迹象明显。循环荷载作用下,强度出现变化的缘由,基本上是因土体剪缩造成正应力降低所致。Aiery等[19]选址于澳大利亚西北大陆架,取材自该区域未扰动钙质土,根据是否胶结展开循环剪切试验,设置差异化循环应力条件,结果显示胶结水平同能承受的动荷载水平呈正相关。各类循环作用下应力状态会表现出无孔隙性水压力累积的弹性状态、少量孔隙水累积的平稳状态、以及孔隙水压力不断集聚之后上升到破坏层级的状态。Salem等选择埃及作为珊瑚砂取材地,而后得出一致结论。虞海珍等研究内容包括:波浪荷载基础上主应力方位循环旋转、初始主应力方位角对松散状态的饱和珊瑚砂(Dr=30%)动强度特性影响研究,观察到是否为均压固结会伴随不同的液化机理,均压固结条件下液化机理为流滑或循环活动性;然而偏压固结状态下无论哪种试验环境都不会产生液化现象。这一主张和Hyodo借助动三轴试验,选择中等密度的Doys Bay珊瑚砂加以观察试验的主张基本一致。虞海珍等[20]、徐学勇等[21]探究了波浪、爆炸负荷条件下钙质砂的动力属性特点,试图解读这类物质在复杂动力荷载影响环境中的动力特性,为相应课题探究奠定了良好的基础。
综上所述,珊瑚砂作为一种特殊介质类型,由于存在明显的颗粒破碎特征,以及多孔性和形状不规则等特征,现阶段国内外对波浪荷载作用下饱和珊瑚砂动力特性试验研究相对较少。国内外相关研究大都基于常规动三轴和常规扭剪试验,忽略了主应力轴旋转问题,故其模拟效果与真实波浪荷载作用有较大差距。本文利用先进的动态空心圆柱扭剪仪HCA-100(美国GCTS公司),对饱和珊瑚砂进行了一系列空心圆柱循环扭剪试验,实现主应力轴连续旋转且应力路径为圆形的特殊应力路径,模拟了不同频率的波浪循环荷载,研究饱和珊瑚砂在动主应力轴连续旋转情况下轴向应变累积特性与孔隙水压力发展模式及波浪荷载循环频率对其的影响。
1 实验设备与试验方法
1.1 试验设备
采用HCA动态空心圆柱扭剪仪,其试样为薄壁空心圆柱,能通过数学推导,由试验加载广义应力路径得出外部荷载加载方式,对其施加扭矩、轴力、内外围压,从而使主应力轴方向产生旋转。
试验采用美国GCTS公司试验仪器试验仪器如图1(a)所示。相对于以往设备HCA-100空心扭剪测试系统,4个外荷载扭矩、轴力及内外围压能够独立地以三角函数、线性或三角波进行加载。能更好的模拟波浪荷载对土体性状的影响,使被研究土体产生主应力轴旋转,研究主应力轴连续旋转的应力路径。空心圆柱状试样应力状态如图1(b)所示。
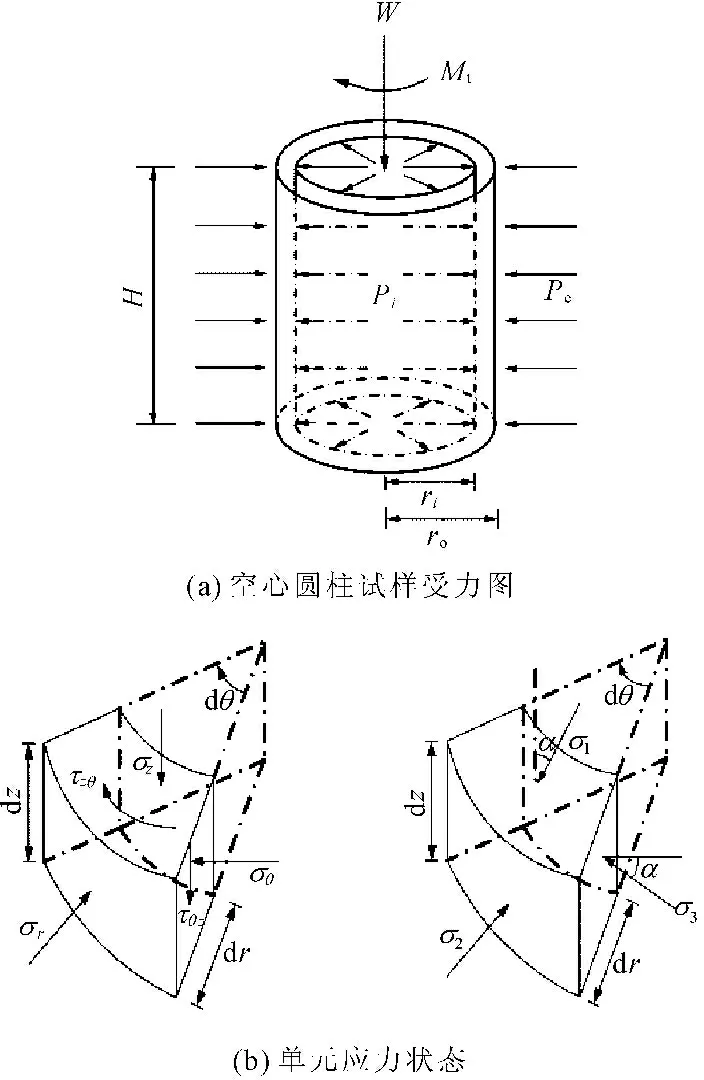
图1空心圆柱试样受力分析
1.2 试验材料
本次试验采用南海群岛永暑岛碳酸钙含量为97.2%的珊瑚砂为研究对象,其基本物理性质指标如下:比重Gs=2.73;最小干密度为ρdmin=1.14 g/cm3;最大干密度为ρdmax=1.43 g/cm3;最大与最小孔隙比分别为emax=1.424,emin=0.895。颗粒级配曲线如图2所示。本次模拟海洋波浪动力荷载作用下主应力轴连续旋转的动态空心圆柱扭剪试验采用薄壁空心圆柱试样,试样高度H=200 mm、外径D=100 mm、内径d=60 mm。制样采用灌砂法并分层击实。
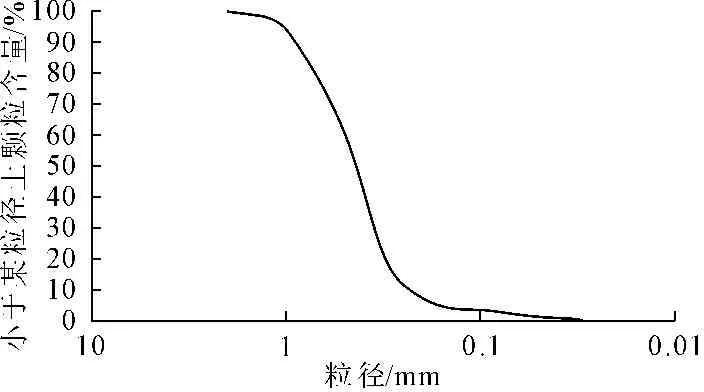
图2级配曲线
1.3 试验方案
波浪荷载其主要特征为主应力轴连续旋转及p、偏应力q保持恒定,在偏应力力系三维应力坐标系b-σ-τ中σ-τ平面的投影为圆心坐标为(p,0)半径为q的圆,为方便计算取偏应力q=(σ1-σ3)/2。
High等[22]推导了外加荷载与单元体所受平均应力之间的定量关系为
(1)
(2)
(3)
(4)
董彤等[23]推导了通过试验所需控制条件设计外荷载的加载公式:
(5)
(6)
(7)
(8)
偏应力q取值为方便计算取:
q=(σ1-σ3)/2
(9)
此处:
E=(ro+ri)/2ro
(10)
F=(ro-ri)/2ro
(11)
G=(ro+ri)/2ri
(12)
H=(ro-ri)/2ri
(13)
(14)
(15)
(16)
本实验取中主应力系数b随大主应力方向角α变化连续变化,能够使试样应变分布更加均匀能更好的研究土体变形。
在坐标系中理论应力路径为圆心坐标为(0,0)半径为30的圆,实际应力路径如图所示。由图3可见理论与实际应力路径基本吻合基本接近圆形。该试验较好的模拟了波浪荷载纯主应力轴连续旋转应力路径。
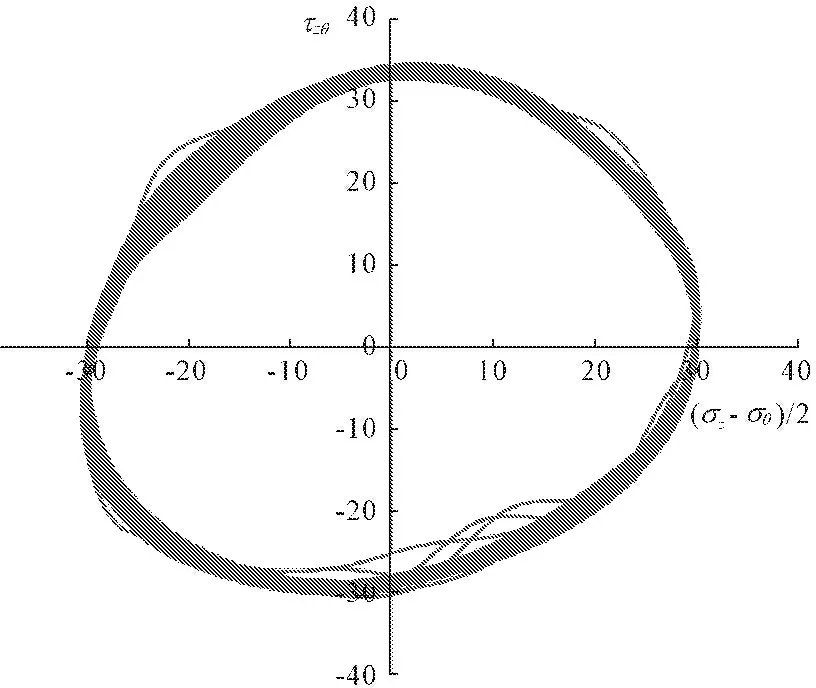
图3试验应力路径
循环荷载加载过程中,在不排水条件下同时施加循环内外围压Pi与P0、循环扭矩Mt和循环竖向荷载W。共进行了6组不同循环频率下的三向非均等固结试验,试验所取偏应力比η=0.433。为研究波浪荷载循环频率对珊瑚砂孔隙水压力发展规律的影响,采用相同级配的珊瑚砂,设置五种循环频率。动荷载循环频率按中国近海波浪荷载循环频率范围取5组试验循环频率分别为0.100 Hz、0.125 Hz、0.150 Hz、0.175 Hz、0.200 Hz,在初始平均有效固结压力为200 kPa下进行试验。钙质砂与普通硅砂的力学性质有明显差别,为与普通硅砂进行对比,对相同级配下的硅砂进行了1组试验,取初始平均有效固结压力为200 kPa动荷载循环频率为0.15 Hz。试验方案详见表1。
1.4 试验终止条件
由试验结果可知,在三向非均等初始固结条件下,其残余孔隙水压力难以达到初始固结平均有效围压,故不采用孔压破坏标准作为试验终止条件。本试验加载应力路径为模拟波浪循环荷载,为控制中主应力系数b=sin2α竖向和扭转及内外围压均采用相位差为π/2的正弦函数耦合加载的方式,较以往试验考虑了中主应力系数变化,使应变分布更加均匀。试样会同时产生轴向与剪切变形,考虑其综合影响不应采用单一应变值作为破坏标准而应以同时包含了两种应变γg的广义剪应变幅值达到10%或循环次数达到10 000次作为试验终止条件。
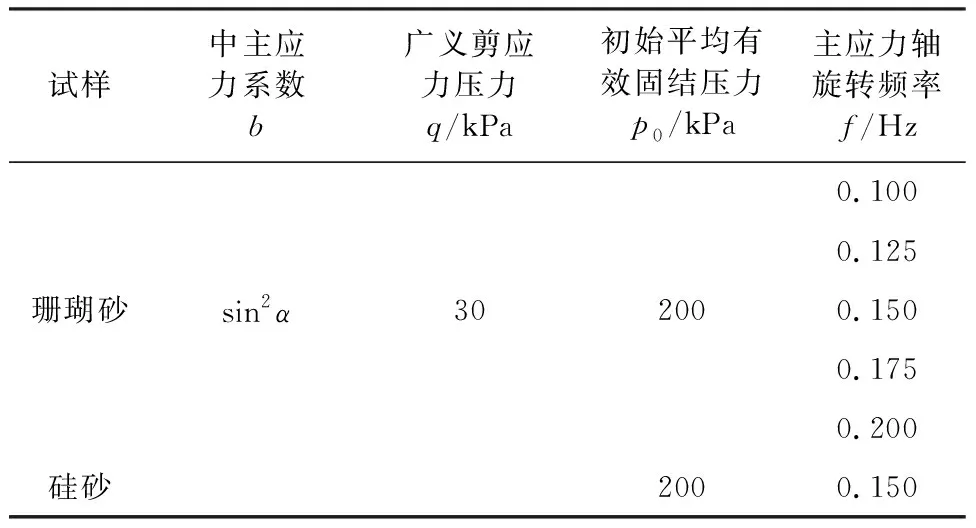
表1 试验方案
2 试验结果与分析
2.1 轴向应变的发展
不同频率循环荷载加载条件下轴向应变基本是先在二分之一循环周期达到一个峰值(总应变符号),而后在后二分之一卸载循环周期减小到一个谷值(回弹应变),并且当一个循环周期终止后依旧存在部分塑性应变(永久应变)。
研究表明,轴向应变随着循环周期的增加不断积聚,并且轴向应变晚期累计速度明显小于早期。详细分析可得,前1 000个循环周期内产生的轴向塑性变形占到了10 000循环周期总变形的五分之三以上。对比试验结果可以发现,虽然不同频率循环荷载加载过程中循环偏应力幅值相同,但是在高频率循环荷载作用下试验得到的永久竖向应变明显大于低频率循环荷载作用下试验所得,并且随着循环圈数的增加二者差距不断增大。波浪荷载广义“圆形”应力路径循环荷载加载过程引起的主应力轴旋转会明显产生和加速轴向应变的累积。通过对比不同频率下轴向应变与循环次数关系曲线,可以发现,在更高频率循环荷载作用下,这种加速效果更加明显,从而导致更多的永久竖向变形的累积。
不同频率循环荷载作用下,竖向应变随着循环圈数变化规律基本相似,但较大频率循环荷载作用下,试验中竖向回弹应变和永久应变都更大。另一方面,随着循环荷载频率增大,主应力轴连续旋转对竖向应变累积的加速作用更加明显。与相同试验条件下循环荷载频率为0.15 Hz的硅砂试验下第10 000圈竖向永久应变的累积量进行对比,由图4可以看出其竖向应变累积模式有显著区别,普通饱和硅砂在前4 000循环周期产生轴向塑性变形才达到10 000循环周期总变形的五分之三以上。饱和珊瑚砂前期轴向应变累计速率明显大于饱和硅砂,但饱和硅砂后期累计轴向应变约为饱和珊瑚砂的两倍。
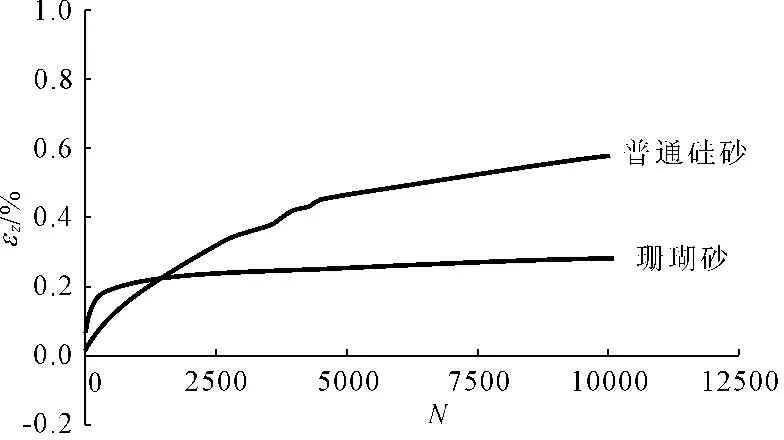
图4试验应力路径
2.2 饱和珊瑚砂孔隙水压力发展模式
当偏应力比η=0.433时,初始平均有效固结压力为200 kp,在频率为0.1 Hz~0.2 Hz循环荷载作用下的饱和珊瑚砂孔隙水压力与振次关系图如图5所示。由图5(a)、图5(b)可以看出饱和珊瑚砂在施加频率分别为0.100 Hz、0.125 Hz的循环荷载后,初期孔隙水压力增长迅速,中期增长趋于平稳,后期孔隙水压力逐渐减小,在小频率下能在10 000次循环内达到负值。呈现“快速增长—平稳增长—下降”的孔隙水压力发展模式。而图5(c)、图5(d)可以看出饱和珊瑚砂在施加频率为0.150 Hz、0.175 Hz的循环荷载后,初期孔隙水压力同样增长迅速,中期趋于平稳,后期孔袭水压力逐渐减小但降低幅值较小并但未降为负值,同样呈现“快速增长—平稳增长—下降”的孔隙水压力发展模式。图5(e)为循环荷载加载频率为0.200 Hz时,饱和珊瑚砂孔隙水压力与振次关系图,如图只能看到孔隙水压力由快速增长到平稳上升。
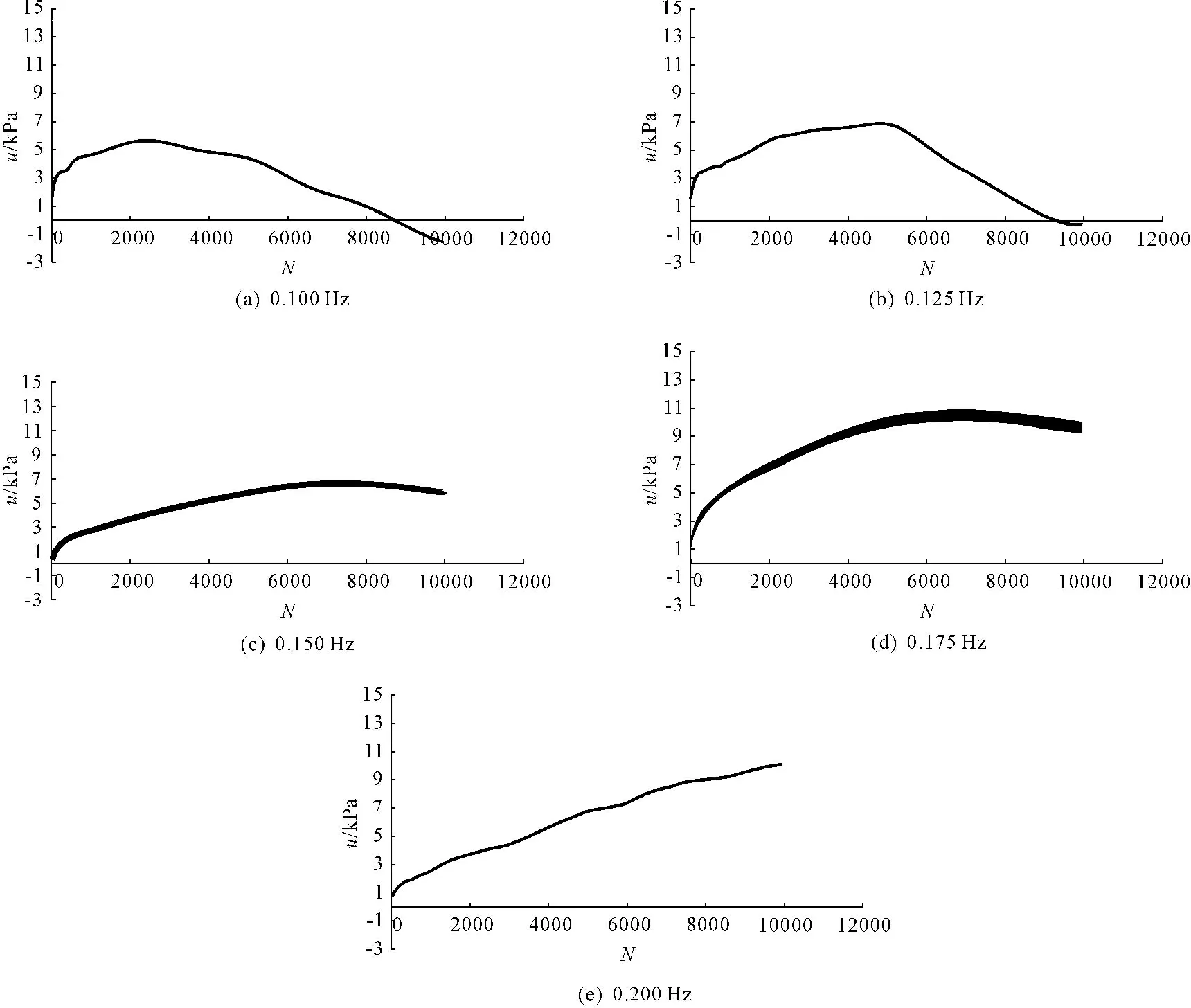
图5不同频率下孔隙水压力~振次关系图
当偏应力比η=0.433,振动频率f=0.15 Hz初始固结压力为200 kPa的饱和硅砂与饱和珊瑚砂孔隙水压力发展规律对比图如图6所示。由图6可以看出饱和硅砂波浪荷载作用下孔隙水发展模式为“快速增长—平稳增长—稳定”的发展模式,而硅砂为“快速增长—平稳增长—稳定”的孔隙水压力发展模式,与饱和硅砂有显著区别。饱和硅砂峰值孔隙水压力为28.3 kPa而饱和珊瑚砂仅为7.1 kPa,在相同条件下峰值孔隙水压力为珊瑚砂的4倍。
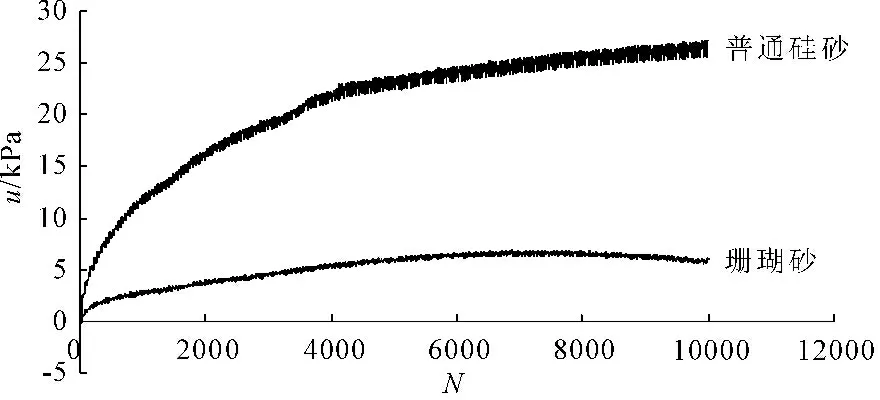
图6硅砂与珊瑚砂孔隙水压力-振次关系图
珊瑚砂在动荷载循环频率在0.100 Hz至0.175 Hz之间这种“快速增长—平稳增长—下降”的孔隙水压力发展模式是由于在第一阶段,珊瑚砂产生体缩使得孔隙水压力迅速上升。第二阶段,珊瑚砂体缩速率逐渐减小孔隙水压力逐渐趋缓。第三阶段土体开始发生剪胀,但同时珊瑚砂在较低应力水平下就会产生颗粒破碎有体缩的趋势,二者同时作用在模拟波浪循环荷载作用下剪胀占优,因此孔隙水压力逐渐下降在低循环频率下甚至可以出现负值,且下降速率由急至缓。表现出中密硅砂的剪胀性,但增长模式有其特殊性。
在波浪动荷载循环频率为0.200 Hz时其孔隙水压力增长模式表现出其特殊性。其发展模式是在高频率下表现出的特殊性或是因振动次数的局限性还有待深入研究。
2.3 振动频率对饱和珊瑚砂孔隙水压力发展模式的影响
饱和珊瑚砂峰值孔隙水压力与振动频率f关系曲线如图7所示。由图7可看出,当振动频率f在0.1 Hz到2.0 Hz之间时,峰值孔隙水压力与振动频率基本呈线性增加的关系。饱和珊瑚砂达到峰值孔隙水压力所需振次Nf(简称峰值振次)与振动频率f关系曲线如图8所示,由图8可看出,峰值振次与振动频率呈线性增加关系。
由以上规律可知,振动频率对饱和珊瑚砂孔隙水压力发展规律具有影响。随着振动频率减小,循环荷载加载时间间隔变长,土体振动变得更加充分,导致土体内阻消耗动应力的能量增加。土体也随之吸收更多能量,因珊瑚砂颗粒易碎性,所以更易发生颗粒破碎,导致珊瑚砂内部结构破坏更加充分,导致孔隙水压力增长速度加快。内部结构破坏加速的同时,提前发生剪涨,使得孔隙水压力上升期变短从而导致达到峰值孔隙水压力所需振次减小,饱和珊瑚砂峰值孔隙水压力减小。在高动荷载循环频率条件下,循环荷载加载间隔时间变短,振动不充分,土体内阻相对低频率条件下消耗动应力的能量减小,孔隙水压力增长速度放缓。孔隙水压力上升期变长,因此出现在动荷载循环频率为0.200 Hz条件下孔隙水由迅速上升到缓慢上升在10 000次循环后还未下降的情况。
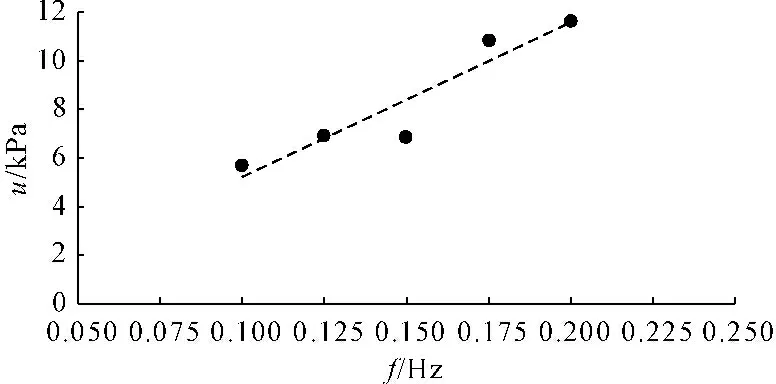
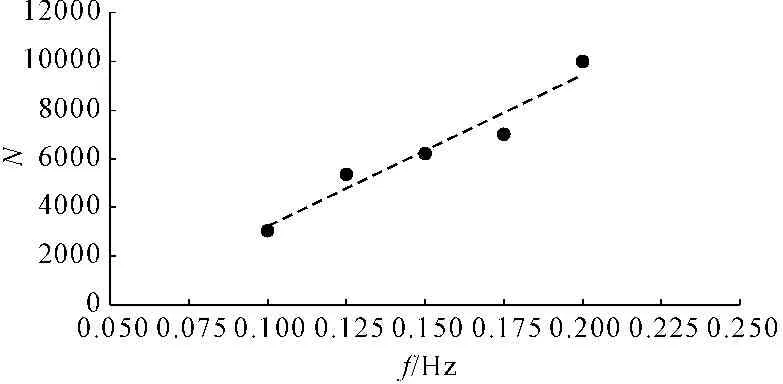
图7 峰值孔隙水压力u-振动频率f关系图
图8峰值振次N-振动频率f关系图
3 结 论
(1) 循环荷载加载过程中轴向应变随着循环周期数的增加不断积聚,并且轴向应变晚期累计速度明显小于早期。且随着循环周期数的增加,回弹模量急剧下降直至1 500个循环时达到稳定。
(2) 波浪荷载广义“圆形”广义应力路径循环荷载加载过程引起的主应力轴旋转会明显产生和加速轴向应变的累积。通过对比不同频率下轴向应变与循环次数关系曲线,可以观察到随着循环荷载加载频率的上升,轴向应变的累计速率及终止轴向应变量均得到增加。
(3) 初始平均有效固结压力为200 kPa,偏应力比为0.433时,在低振动频率(f=0.100~0.175 Hz)下,饱和珊瑚砂孔隙水压力呈“快速增长—平稳增长—下降”的增长模式;当振动频率为0.200 Hz时饱和珊瑚砂孔隙水压力呈“快速增长—平稳增长”的特殊增长模式。
(4) 不同振动频率条件下饱和珊瑚砂峰值孔隙水压力均较低。在初始平均有效固结压力为200 kPa振动频率为0.150 Hz条件下,饱和珊瑚砂峰值孔隙水压力仅为饱和硅砂的1/4。
(5) 在本文研究的条件下,随着振动频率的增加,饱和珊瑚砂峰值孔隙水压力与振动频率基本呈线性增加关系;峰值振次与振动频率呈线性增加关系。振动频率对饱和珊瑚砂孔隙水压力发展模式有显著影响。
