基于动量平衡的多离子体系扩散模型
2018-11-06张志红巨占莹
张志红,陈 杨,巨占莹,郭 飞
(1.北京工业大学 城市与工程安全减灾教育部重点实验室, 北京 100124; 2.北京市政建设集团有限责任公司, 北京 100048)
扩散是众多工程领域中普遍存在的现象[1-5]。环境岩土工程领域中,垃圾填埋场和疏浚底泥堆场多采用压实黏土作为衬垫系统或防渗隔污屏障。黏土垫层作为典型的多相孔隙介质,在服役期间表现为一个开放的热力学系统,服役环境具有独特的特点。首先,渗滤液是由多种可溶性离子和水组成的多离子体系,离子与离子间的复杂物理化学作用对单种离子的扩散过程产生明显的影响,已经通过扩散系数的变化得到了试验证明。其次,与离子在开放液体中的扩散相比,离子在黏土屏障中扩散时,离子与黏土骨架间的碰撞与摩擦作用将直接影响其扩散过程,表现为离子在黏土中的扩散系数小于其在开放液体中的扩散系数。同时研究发现,多离子体系中,如果离子浓度较高,则溶液的非理想性增强,单种离子的活性受到抑制,从而致使单种离子参与运动的浓度并不能得到全部有效发挥[6]。因此如何正确描述多组分溶质离子共存复杂情况下的离子扩散运动是一个亟待解决的问题。
国内外学者采用传统方法对离子在孔隙介质中的扩散开展了相关研究工作。陈云敏[7]、谢海建[8]等考虑污染物在土体中的吸附和分子扩散,并引用Fick第二定律,建立了单组分污染物在黏土中的一维扩散模型。Muniruzzaman、Rasouli考虑组分离子间的静电力作用分析了多组分扩散规律[9-13]。但已有研究成果缺乏对多组分(多离子)并存条件下浓度特征的描述。本文采用线性动量平衡的方法,将活度系数引入多离子体系的组分微观平衡方程,基于有效浓度描述的多离子体系组分微观质量和动量平衡方程,采用体积平均技术建立了多离子体系宏观非线性扩散模型,所建模型既能实现对非线性扩散过程的准确描述又能蕴含微观信息。
1 基本假定
(1) 土体是由土体骨架和孔隙液相组成的饱和均质两相介质。
(2) 土体骨架是刚性的,即不考虑土体骨架的变形。
(3) 孔隙液相是多离子体系,是孔隙水和N种可溶性离子组成的混合物,即孔隙液相是N+1种组分组成的混合物。
2 微观平衡方程
孔隙液相作为多离子体系,离子间的复杂作用使得单种离子的活性受到抑制而不能发挥出其初始输入浓度值大小的作用,因而需要引入活度系数反映离子的有效浓度与其实际浓度的差异。活度系数的引入,既能反映其它离子的存在对单种离子运动起到的推进或阻滞作用,从而更加准确真实地描述多离子体系的运动规律;又能将活度系数作为一个未知量从理论上引入到扩散模型中,有利于在统一的理论框架内建立活度系数的本构模型。
多离子体系组分i(i=1,…,N+1)的微观质量平衡方程[14]:
(1)
其中:ρi为组分i(i=1,…,N+1)的微观质量密度(质量浓度),即单位液相体积中组分i(i=1,…,N+1)的质量,vi为组分i(i=1,…,N+1)的微观速度。
将描述组分活性的活度系数引入方程(1),即得用有效浓度表示的孔隙液相i(i=1,…,N+1)组分的微观质量平衡方程:
(2)
式中:ri为组分i(i=1,…,N+1)的微观活度系数。
组分i(i=1,…,N+1)的微观动量平衡方程:
(3)
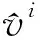
将活度系数引入方程(3),即得有效浓度表示的孔隙液相i(i=1,…,N+1)组分的微观动量平衡方程:
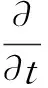
(4)
3 体积平均
3.1 代表性单元体积
多相孔隙介质的宏观行为与固体基体的微观结构和微观尺度物理具有直接联系[15],因此本文采用Bear提出的代表性单元体积的概念。图1给出了饱和两相介质宏观域、宏观点和REV的关系。宏观场中,饱和两相介质的体积是V,边界是A。宏观域V中的每个宏观点都是一个REV的中心。一个REV的体积是ΔV,边界面积是ΔA。在ΔV中,固相s的体积是ΔVs,液相f的体积是ΔVf。与之类似,REV边界面积ΔA中,固相s占据的部分是ΔAs,液相占据的部分是ΔAf。此外,REV内固相和液相的界面面积是ΔAfs。REV内任一点的位置矢量用r表示,满足r=x+ξ,ξ是相对于质心坐标x的微观坐标。
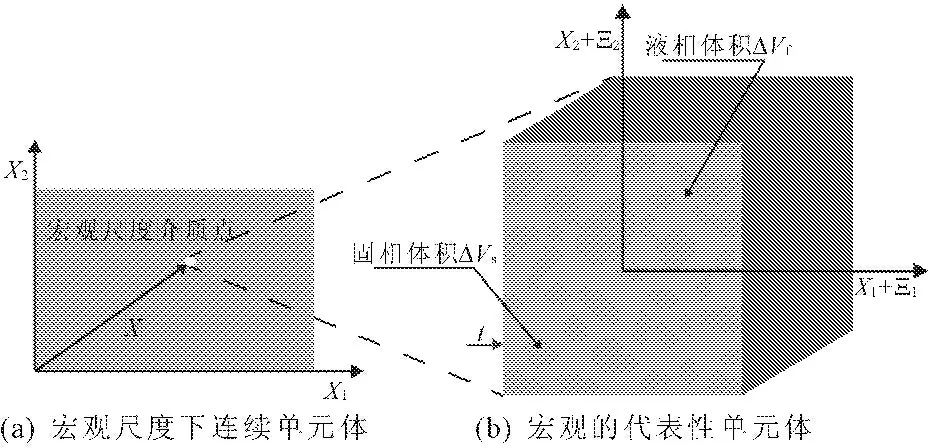
图1饱和两相介质代表性单元体示意图
REV内,α(α=s,f)相的体积可以通过对其分布函数γα进行积分得到:
(5)
式中:X和ξ分别是宏观和微观坐标。分布函数定义如下:
(6)
因此,α(α=s,f)相的体积分数为:
(7)
且
(8)
3.2 宏观平均量的定义
基于Hassanizadeh和Gray确立的定义宏观平均量的四条准则,本文涉及到的宏观物理量定义如下:
(ΔV内f相组分i(i=1,…,N+1)的平均质量密度函数)
(ΔV内f相组分i(i=1,…,N+1)的平均活度系数)
vi(r,t)γf(r,t)dv(ξ) (ΔV内f相组分i(i=1,…,N+1)的质量平均速度)

4 宏观平衡方程
将组分i(i=1,…,N+1)的微观质量平衡方程式(2)和微观动量平衡方程式(4)乘以孔隙液相的分布函数,然后在代表性单元体积上积分再平均,即得f相组分i(i=1,…,N+1)的宏观质量和动量平衡方程:
(9)
(10)

(11)
nfda

孔隙液相的应力张量是其所有组分的部分应力张量之和,即:
(12)
其中:p为静水压力,δ为单位张量,τf为各向异性偏应力张量。定义为:
(13)
则孔隙液相应力张量的散度为:
(14)
热力平衡条件下,等温体系的Gibbs-Duhem方程为:
(15)
相应地,有效浓度描述的f相组分i(i=1,…,N+1)的Gibbs-Duhem方程可描述为:
(16)

(17)


(18)
将热力学关系(17)代入式(18),得:
(19)
最后,将式(19)带入组分i(i=1,…,N+1)的动量平衡方程式(10)得:
(20)
式(20)即为采用化学势梯度描述的孔隙液相中组分i(i=1,…,N+1)满足的动量平衡方程。
至此,得到了能够反映微观信息的孔隙液相中组分i(i=1,…,N+1)的宏观质量平衡方程式(9)和宏观动量平衡方程式(20)。且在平均化的过程中得到了孔隙液相组分与土体骨架间的相互作用以及孔隙溶液中组分与组分间的相互作用。与已有的研究相比,本研究将组分i(i=1,…,N+1)的活度系数作为一个独立参量引入到了其宏观质量和动量平衡方程中,构建了一个有效浓度描述的多离子体系在多相孔隙介质运移的理论框架。
5 本构方程
5.1 化学势本构
化学势是温度、压力和组分质量分数的函数,则f相内i组分化学势的本构关系为:
(21)

(22)
其中:ρf为孔隙液相的密度。
则等温等压下,组分i(i=1,…,N+1)的化学势梯度为:
(23)
式中:Γij是热力学因子,定义为:
(24)
其中:δij是克罗内克函数。
5.2 活度系数
多孔介质中孔隙液相离子的活度系数与离子间相互作用密切相关,Guggenheim等对Debye-Huckel理论进行修正,得到了孔隙液相中组分i(i=1,…,N+1)的活度系数表达式:
(25)
式中:A和B的值为取决于水的介电常数、密度和温度;a与离子有效直径 (水化半径)有关;zi表示离子的电荷数;b可通过试验数据获得;I为组分的离子强度。
5.3 多离子体系内部作用力
(26)

(27)

Bearman和Kirkwood给出了浓度梯度作用引起的相对运动产生的摩擦力本构方程,即:
(28)
式中:ζij是组分间摩擦系数,且ζij>0。
温度梯度作用导致相对运动产生的摩擦力本构方程为:
(29)

(30)
将式(30)代入式(27),得到i(i=1,…,N+1)组分的内部作用力的具体表达式为:
(31)
5.4 部分偏应力张量
在多组分混合物流体中,某一组分的部分偏应力存在多种本构形式,本文选用Bird给出的形式:
(32)
式中:ηi为第一黏性系数或动力黏性系数,λi为第二黏性系数,均可通过试验测得。
5.5 离子与土骨架间的摩擦力
(33)
6 多离子体系扩散模型
将本构方程(23)、(25)、(31)、(32)和(33)代入到组分i的宏观动量平衡方程式(20)中,得:
(34)
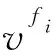
(35)
式(35)即为从微观动量平衡方程出发,应用体积平均技术和经典力学方法,得到的多离子体系宏观扩散方程表达式。该方程能够考虑多离子体系的离子活度对单种离子扩散过程的影响,并由活度系数反映。同时,该扩散方程考虑了离子间摩擦力以及离子与黏土骨架间摩擦力对单种离子扩散速度的影响。
7 结 论
基于多离子体系组分(离子和水)的微观平衡方程和体积平均技术建立了多离子体系宏观非线性扩散方程的理论框架。本文所建模型简单化和基础性便于工程实践应用,为设计合理、经济的防渗系统提供了理论依据,对于堆场防渗系统的设计及隔污垫层长期有效评估具有重要的实际意义。
