基于完全耦合理论的涉水边坡地震响应分析
2018-11-06靳聪聪迟世春聂章博
靳聪聪,迟世春,聂章博
(1.大连理工大学 建设工程学部, 辽宁 大连 116024; 2.大连理工大学 海岸与近海工程国家重点实验室, 辽宁 大连 116024)
为了加速我国中西部地区的经济发展,一大批的水利、交通、能源等基础建设工程陆续开工,相应的工程边坡数量激增。由于这些区域内相当比例工程边坡位于中、强震地区,加之近些年我国地震活动频度高和强度大,造成了各类工程和自然边坡的破坏,严重危及人民群众生命财产安全。如“5.12”汶川大地震诱发的大型、特大型滑坡达数百处,具有危害的边坡多达6 000余处[1]。与此同时,库水位变化、降雨等外部因素也是诱发滑坡的原因[2],尤其是位于河流水系丰富区域的涉水边坡在地震作用下更容易产生滑坡。相比结构工程的抗震研究,边坡的抗震研究比较滞后,其中地震作用下边坡的动力响应的研究一直是国内外岩土工程界的研究的难点[3]。
国内外专家学者对该问题从理论研究、试验模拟到数值分析做了大量深入系统的研究,取得一系列有价值的成果。通过振动台[4]和动力离心机模拟试验[5]对边坡动力响应模拟,能够模拟地震荷载下边坡动力响应情况,能够科学合理的对有限元等数值分析结果比对。但是鉴于试验法技术复杂,设备要求高,对于边坡动力响应更多的是采用数值方法进行分析。有限元法是最早应用于岩土边坡动力分析的数值方法,可较好考虑地震荷载作用下的各种地形、边界条件、材料特性等因素的影响[6-7]。
目前,考虑水土完全耦合作用的弹塑性地震动力分析成为研究岩土工程动力响应的有效方法[8],该方法可以直接求解永久位移和超静孔隙水压,并能合理分析超静孔压的累计消散过程以及残余变形情况。黄雨等[9]采用水-土完全耦合理论对地面沉降进行分析。李荣建等[10]采用基于Biot三维固结理论开发的三维有限元程序对VELACS试验和原型土坡进行动力分析。本文采用PZC弹塑性模型[11]结合完全耦合理论,通过三维弹塑性动力固结程序DYNE3WAC[12-13]对某涉水边坡进行动力响应研究,全面分析该边坡加速度反应、超静孔压、边坡变形,且计算结果满足一般规律,说明该理论的正确性。分析在不同水位工况下涉水边坡受到地震作用时的坡顶永久变形情况,根据水位-时间-坡顶竖向永久变形的三维曲面图可知,随着水位的增加,涉水边坡在地震作用下的沉降值不断增加,坡顶的大变形极易引起边坡失稳,因此抗震设计时须对此处引起重视。
1 完全耦合理论
完全耦合理论是基于Biot动力固结方程,考虑土体的变形和液体运动的相互作用,在分析过程中,孔隙水压力的累积和消散与土的变形是完全耦合,并且可以考虑土骨架的非线性、弹塑性等特性。该理论可确定地震条件下孔隙水和土骨架组成的应力、孔压以及变形的分布。对于包括地震工程在内的大部分中低振动频率的工程问题,可忽略流体相对加速度,包含基本未知量u和p的饱和土体动力固结控制方程(u-p形式)如下所示:
(1)
(2)
式中:σij为总应力;ρ为土体饱和密度;ui为土体位移;bi为单位质量上的力;α和Q为土体和流体的压缩性相关的系数;εij为土体应变;k为动力渗透系数;p为孔隙水压力。
采用Galerkin加权残量法和分部积分法对式(1)、式(2)微分方程进行离散,得到饱和土动力平衡方程的有限元离散形式。
(3)
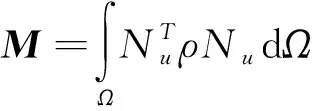
饱和土中的流体有限元离散形式如下:
(4)

采用广义Newmark法对式(3)、式(4)进行积分,其中对位移u采用二阶积分方案,即:
(5)
式中:β1和β2是积分参数。
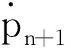
(6)
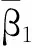
(7)

2 PZC弹塑性本构模型
目前成功应用于土质边坡的动力本构模型还比较少,而Pastor,Zienkiewicz和Chan基于广义塑性理论建立了著名的PZC本构模型已广泛应用于土工抗震中。该模型区别于传统意义上的需假设塑性势面和关联流动法则的塑性理论,该模型无需建立显式的屈服函数和塑性势函数,而是直接确定塑性流动方向和加载方向,并且采用非关联流动法则。根据剪胀比dg和应力比η的试验结果发现剪胀方程近似表示为:
dg=(1+αg)(Mg-η)
(8)
式中:αg和Mg为模型参数;η为应力比;Mg的表达式为:
(9)
式中:φc为残余内摩擦角;θ为罗德角。
PZC弹塑性本构模型的塑性流动方向如下所示:

(10)
该模型的加载方向为:
(11)
df=(1+αf)(Mf-η)
(12)
式中:αf和Mf为模型参数。
加载时的塑性模量HL表达式如下所示:
HL=H0·p′·Hf·(Hv+Hs)·HDM
(13)

卸载时塑性模量如下所示:
(14)
式中:Hu0和γu为模型参数。
PZC模型的弹塑性矩阵Dep如下所示:
(15)
将公式(15)代入公式(3)后,即可将描述砂土特性较好的PZC模型和完全耦合结合,因此将基于完全耦合理论和PZC弹塑性本构模型编制的SWANDYNE II[14-16]可以很好的模拟地震作用下的土工结构的动力响应。该程序是国际上著名的动力固结有限元程序,并在三十年中成功应用于地基、土石坝、边坡等土工和水工建筑物的静动力分析中。DYNE3WAC是SWANDYNE程序的三维版,该版本较二维的SWANDYNE程序能够更加准确的对土工结构进行动力响应分析。
3 涉水边坡地震动力响应分析
3.1 有限元模型
本文计算采用的概化涉水边坡的断面示意图如图1所示,地基为美国国家自然科学基金资助的项目VELACS的Dr=60%的Nevada砂地基,厚8 m。边坡填筑材料也采用Dr=60%的Nevada砂,高度为10 m。取长×高=55 m×18 m的区域为模拟范围,边坡厚为6 m,坡比为1∶2,坡顶后缘长度为15 m,设计水位距边坡地基处的水深为6 m。

图1涉水边坡断面示意图
如图1所示,对涉水边坡的6个分别位于坡脚点、坡面中点和坡顶点的典型点的加速度、超静孔压、变形等特性进行动力响应分析。对边坡进行有限元网格划分,建立三维有限元网格如图2所示,得到单元2 700个,其中六面体和楔形单元均采用二次单元,即角结点同时拥有位移和孔压自由度,边中结点仅有位移自由度,结点数为8 092个。
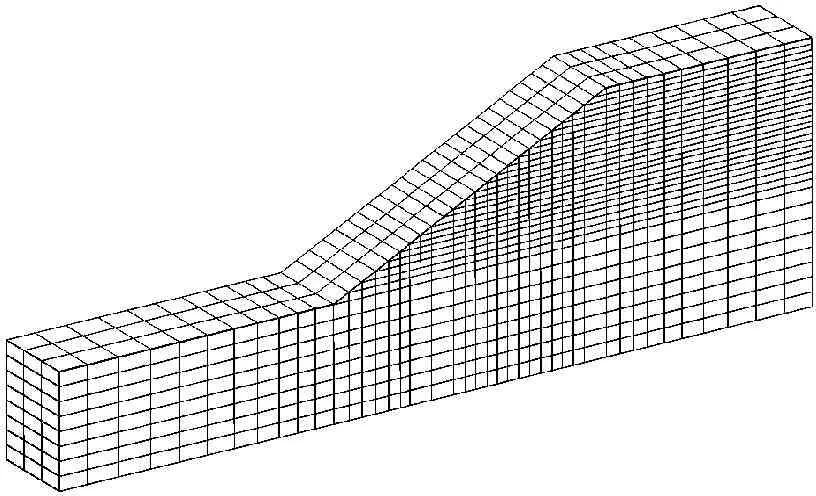
图2三维有限元模型
3.2 材料参数及地震动输入
概化边坡采用材料的物性参数,如土粒比重、孔隙比、渗透系数等,如表1所示。

表1 Nevada砂物性参数
Nevada砂进行了单调加载三轴试验和循环荷载试验,以确定其力学参数,采用基于MATLAB可视化的参数标定程序SM2D来标定PZC弹塑性本构模型参数[13],如表2所示。

表2 PZC弹塑性模型参数
地震波从底面沿y方向输入,输入单向地震波作用于该涉水边坡方向进行水平振动,输入地震波如图10所示,其峰值加速度为0.198g,地震波计算时间取35 s,对应的地震动时程曲线如图3所示。
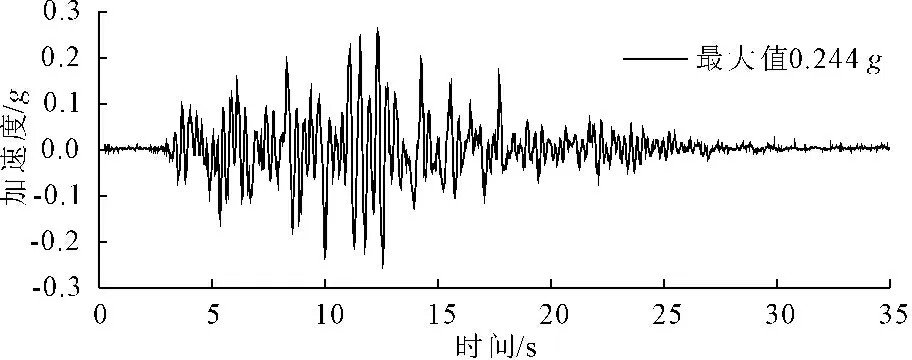
图3输入地震动
3.3 涉水边坡动力响应分析
采用基于DYNE3WAC动力固结程序对边坡进行动力响应分析,主要对典型土质点的加速度时程、超静孔压、位移响应和坝体的永久变形等情况进行分析。然后考虑不同水位工况下的坝体典型点位移响应,建立时间-水位-位移的三维曲面图,直观的分析水位变化对涉水边坡动力响应的影响。其中图4给出了边坡上典型点A、B、C(如图1所示)加速度响应计算结果,从绘制的3个典型点的加速度-时程曲线与边坡底部加速度-时程曲线进行对比可知,从底部到C点,加速度响应先稍微减弱,即从0.244g降至0.215g,而后显著变大,到B和A的加速度峰值分别为0.263g和0.297g,呈明显的鞭梢效应。
3个典型点能够较好的描述地震作用下边坡加速度响应规律,反应了在地震过程中,坡体对输入地震波的放大作用,同时又合理体现边坡土体的阻尼对传输的地震波中的高频部分的滤波效果,符合一般规律。

图4加速度时程曲线
三维边坡中B到F的5个不同深度处典型点的超孔隙水压力在地震动作用下的响应如图5所示。
由图5可知,该处边坡中的5处典型土质点的超静孔压时程曲线能够很好的反映出地震动作用下的超静孔压扩散的趋势。边坡中部位置(B、C)、边坡中部地基位置(D)和坡脚位置地基中(E、F)的超静孔压峰值分别为41.3 kPa、72.9 kPa、87.8 kPa、42.9 kPa、63.5 kPa。5处土质点的位置和超静孔压值能够合理的反映地震动作用下的孔压增长情况。地震过程中,随着边坡增高方向,对应典型点的超静孔压不断减小,从D点到C点再到B点,对应的峰值孔压逐渐减小,另外,E点较F点处的峰值孔压也较小。同一高程的典型点,位于右侧的超静孔压增长大于左侧超静孔压增长,C和D点均大于同一高程的左侧的E和F点的峰值孔压。

图5超静孔压时程曲线
为进一步分析边坡的变形情况,对该处边坡在地震动作用下的竖向永久变形的变化规律进行研究,计算分析时采用向下为正,涉水边坡的竖向沉降等值线如图6所示。
图6给出了计算得到的边坡地震35 s时刻的竖向位移分布,可以看出边坡残余变形符合一般规律,沉降最大值为0.91 m,位于坡顶处。为了进一步分析涉水边坡在动力情况下的位移响应情况,图7给出了对典型点A的位移时程曲线。


图6 竖向沉降等值线图(单位:m)
图7典型点A位移时程曲线
由图7可知,在 0~4 s之间,位移变化幅度很小,主要是因为该时段内的地震动PGA较小,随着地震动强度的不断增大变化,边坡典型土质点A处对应的竖向永久变形显著增加,25 s左右达到沉降最大值为0.91 m。
通过对涉水边坡在设计水位下的动力响应进行分析,为更好的分析边坡在不同水位深度的动力响应,尤其是竖向永久变形的位移时程变化情况。采用DYNE3WAC弹塑性动力有限元程序对不同水位的边坡进行动力分析,而后绘制时间-水位-位移的三维曲面图进行进一步的位移时程分析,如图8所示。
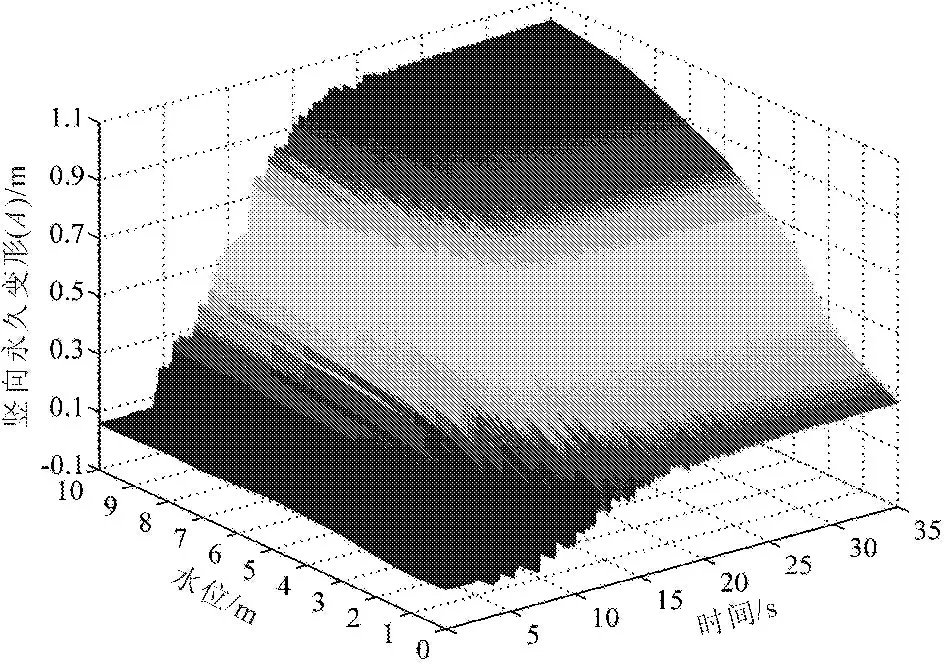
图8位移时程三维曲面图
通过图8可知,随着水位的升高,边坡永久位移表现出不断增加的趋势。无水时的边坡永久变形仅为0.31 m,当水位为10 m时,边坡永久变形达到1.22 m。由三维位移时程曲面图8可知,水位对涉水边坡在地震作用下的变形影响是显著的,高水位时的涉水边坡遭遇地震荷载时极易发生大变形破坏,进而引起边坡的失稳,因此需要对高水位时的涉水边坡进行适当的抗震措施。
4 结 语
本文介绍了基于完全耦合的弹塑性动力有限元方法,该方法能够考虑涉水边坡在动力作用下的水土耦合,采用的PZC弹塑性本构模型能够描述边坡材料的力学性质。通过有限元程序的分析可知,该处边坡的加速度在涉水边坡先稍微减弱而后逐渐增大,呈现出鞭梢效应,边坡的超静孔隙水压力随地震动变化并逐渐累积,竖直向永久位移的最大值发生在坡顶处。通过对涉水边坡在水位变化的位移时程三维曲面分析可知,随着水位的增加,涉水边坡在地震作用下的沉降值不断增加,坡顶的大变形极易引起边坡失稳,因此在涉水边坡的顶部区域的抗震设计需要重点关注的。
