最小二乘支持向量机的点云数据孔洞修补算法

杨永强, 李淑红

(河南财经政法大学 计算机与信息工程学院, 郑州 450002)

点云处理技术在逆向工程、 精密制造、 数字化文物、 机械设计等领域应用广泛[1-2]. 在点云数据采集过程中, 由于技术条件限制及外界因素的影响, 不可避免会出现点云数据缺失现象, 出现一些孔洞, 对后续点云数据建模过程产生不利影响. 因此, 为了保证模型的完整性, 在进行点云数据建模前, 首先要实现孔洞修补[3].

目前, 已有许多点云数据孔洞修补算法[4-5], 传统点云数据孔洞修补算法主要分为两类： 基于体积元素的算法和基于三角网络的算法. 其中基于体积元素的算法采用体积元素描述物体修补模型, 如: 文献[6]提出了基于体积离散的点云数据孔洞修补算法, 可有效修补有岛屿面片的物体模型, 但易改变物体模型的结构； 文献[7]提出了基于空间雕刻与等值面相融合的点云数据孔洞修补算法； 文献[8]提出了基于最小切割算法的点云数据孔洞修补算法, 通过估计物体模型内部和外部边界实现复杂物体模型的修补. 基于三角网格的算法采用三角网格描述物体修补模型, 如: 文献[9]提出了基于Poisson方程重构的点云数据孔洞修补算法； 文献[10]提出了基于差分进化理论的点云数据孔洞修补算法; 文献[11]提出了基于径向基函数(RBF)的点云数据孔洞修补算法; 文献[12]提出了基于移动最小二乘法的点云数据孔洞修补算法. 当点云数据分布均匀, 且数据规模较小时, 该类算法可得到理想的点云数据孔洞修补效果, 但当数据规模较大时, 修补过程费时, 很难取得好的修补效果. 将神经网络、 支持向量机应用于点云数据孔洞修补中, 通过其自适应、 自组织学习能力, 实现点云数据的轮廓构建与曲面拟合, 其云数据孔洞修补效果优于传统算法[13]. 但在实际应用中, 神经网络的结构复杂, 收敛速度慢, 易产生局部极小值, 支持向量机的训练时间较长, 不能满足点云数据孔洞修补实时性的要求. 最小二乘支持向量机(least square support vector machine, LSSVM)[14]对标准支持向量机进行简化, 克服了神经网络易产生局部极小值的缺陷, 且具有支持向量机良好的泛化能力, 为点云数据孔洞修补提供了一种新技术.

为了获得理想的点云数据孔洞修补结果, 本文提出一种基于最小二乘支持向量机的点云数据孔洞修补算法. 首先根据散乱点云边界估计孔洞修补范围, 然后根据孔洞及周围点的信息, 采用最小二乘支持向量机建立曲面, 实现点云数据的孔洞修补, 最后通过仿真实验验证本文算法的有效性. 结果表明, 最小二乘支持向量机能有效修补各种复杂的孔洞, 具有一定的实际应用价值.

1 最小二乘支持向量机

标准支持向量机采用不等式约束, 训练过程较复杂, 耗时较长, 且待确定参数较多, 因此无法应用于大规模云数据孔洞修补中. 而最小二乘支持向量机把不等式约束变为等式约束, 加快了训练速度, 简化了参数优化, 可更好地满足大规模云数据孔洞修补的要求. 设训练集为{(xi,yi)},i=1,2,…,k,xi∈n,yi∈,xi和yi分别为输入向量和期望输出, 采用函数φ(·)对原始训练集进行映射, 得到LSSVM的回归方程为

f(x)=wTφ(x)+b,

(1)

其中w和b分别表示权值和偏置. 基于结构风险最小化原理, 式(1)等价于

(2)

其中:γ为正则化参数；ei为回归误差.

为了简化LSSVM学习的过程, 提高学习效率, 引入Lagrange乘子αi对式(2)进行转换, 得到其对偶空间优化模型为

(3)

(4)

对于非线性问题, 通过引入核函数K(xi,xj)=φ(xi)Tφ(xj)得到LSSVM的回归函数为

(5)

采用RBF构建LSSVM, 其定义为

(6)

式中σ为宽度参数. 基于RBF函数的LSSVM回归函数为

(7)

在LSSVM建模过程中, 参数γ和σ直接影响回归结果的优劣, 因此通常要进行最优参数的确定, 参数σ的变化范围定义为

k1dmin=σl<σ<σu=k2dmax,

(8)

其中dmin和dmax分别为训练集的最小和最大距离. 若σl太小则将导致过拟合, 若σu太大则覆盖范围较大, 学习复杂程度较高, 本文设σ参数取值范围为[0.001,1 000], 采用粒子群算法[15]按图1所示流程确定参数γ和σ.

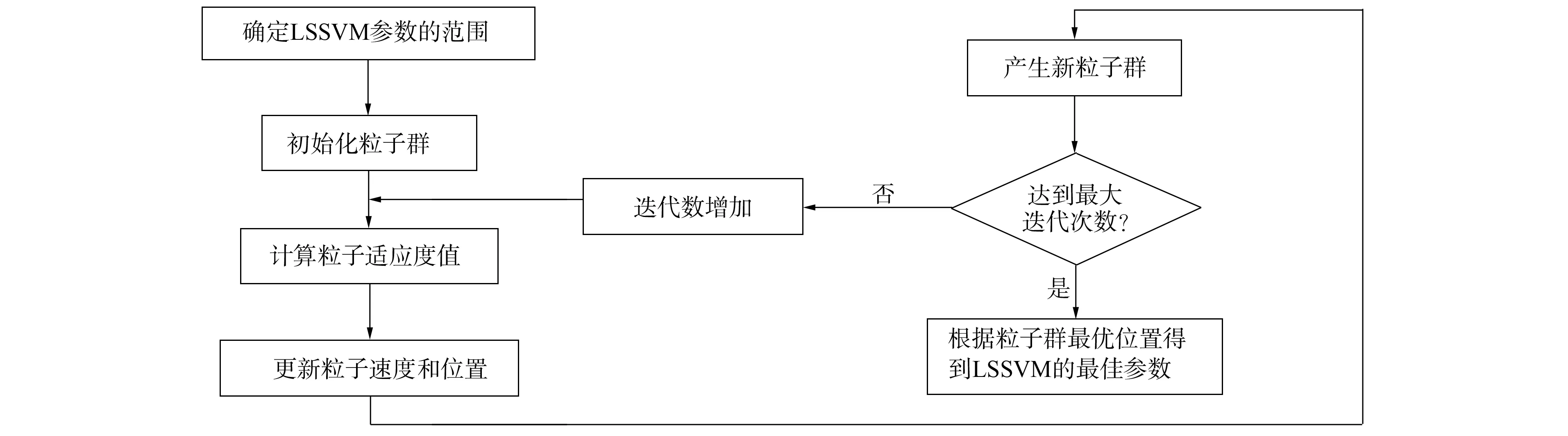
图1 LSSVM参数的确定流程Fig.1 Determination procedure of LSSVM parameters

2 改进算法

2.1 检测孔洞 在点云数据孔洞修补过程中, 首先进行孔洞检测. 孔洞检测结果的优劣直接影响后续孔洞修补效果, 是孔洞修补的基础, 步骤如下：

1) 根据点云数据孔洞修补问题, 在点云数据孔洞边缘上选择多个数据点；

2) 根据这些点云数据点拟合曲线边界的控制顶点, 得到边界曲线；

3) 对产生的新曲线, 在其边界重新采样, 即可得到点云数据孔洞修补的新增点；

4) 根据原边界点与新增采样点, 得到孔洞边界, 实现孔洞的检测.

2.2 估计孔洞邻近域 孔洞及其附近的几何信息共同组成了点云数据孔洞修补的孔洞邻近域, 而附近几何信息可根据邻近域的半径进行选择, 设孔洞所在面与邻近域内各点P1,P2,…,Pn的平方和最小, 则表示该面为特征面, 能用空间点O和单位法向量n描述, 从而有

(9)

若点云数据的某一孔洞邻近域为P1,P2,…,Pn, 设d(Pi,O)≥d(Pj,O), 则近域的最远数据点为Pd,d(x,y)为x和y两点之间的距离,O为原点, (Pd-O)×n,n×((Pd-O)×n),n分别为u轴、v轴、s轴, 其共同组成一个孔洞坐标系, 其中uv位于同一个平面上,v轴表示孔洞较狭小的方向.

(10)

因此可通过LSSVM实现曲面拟合, 步骤如下：

1) 给定样本集T, 确定LSSVM核函数及参数, 参数采用粒子群优化算法确定;

2) 构造并求解最优问题, 得到其解为

(11)

(12)

4) 构造曲面拟合函数为

(13)

3 点云数据孔洞修补算法的性能测试与分析

为了分析点云数据孔洞修补算法的效果, 采用测试平台： Intel Core i7 6800K(3.4 GHz/L3 15M)的处理机, 技嘉X99-Phoenix SLI主板, 32 GB DDR4的内存, NVIDIA GeForce GTX 1070的显卡, 256 GB的SDD硬盘, 内置10-100-1000M网卡, Windows10的操作系统. 用标准C++语言和OpenGL图形编程接口实现点云数据孔洞修补算法, 实验对象为花瓶和兔子, 本文算法首先提取散乱点云边界, 然后对点云数据孔洞进行修补, 实验结果如图2所示.

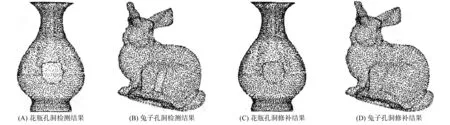
图2 点云数据修补结果Fig.2 Results of point cloud data repairing

为了进一步测试本文算法的优越性, 选择文献[7]、 文献[8]和文献[10]的点云数据孔洞修补算法进行对比实验, 对比结果列于表1. 由表1可见, 相对于对比算法, 本文算法的孔洞修补成功率大幅度提高, 且修补耗费时间也有所下降, 加快了点云数据孔洞修补的速度, 获得了更理想的点云数据孔洞修补效果.

表1 不同点云数据修补算法的性能对比

综上所述, 本文针对当前点云数据孔洞修补算法耗时长、 修补效果不理想的问题, 提出了一种基于最小二乘支持向量机的点云数据孔洞修补算法, 充分利用孔洞边界点和邻域信息, 采用最小二乘支持向量机建立曲面函数, 实现孔洞修补点与原始点云的平滑过渡, 获得了理想的修补效果.