分数阶Newton-Leipnik混沌系统 滑模同步的两种方法
2018-11-06毛北行
毛 北 行
(郑州航空工业管理学院 理学院, 郑州 450015)
近年来, 对滑模同步问题的研究已引起人们广泛关注[1-10]. 文献[11]研究了一类分数阶Duffling-Van der pol系统的同步控制问题; 文献[12]研究了分数阶多涡卷系统的同步控制; 文献[13]基于滑模方法研究了一类不确定系统的同步问题; 文献[14]研究了一类具有二次项的Mavpd混沌系统的动力学分析问题, 并讨论了该系统的平衡点及稳定性; 文献[15]研究了比例积分追踪制导方法, 得到了精确的追踪制导方法; 文献[16]研究了一个新混沌系统的滑模控制问题. 在此基础上, 本文研究分数阶Newton-Leipnik混沌系统滑模同步, 并给出系统取得同步的充分性条件.
定义1[17]Caputo分数阶导数定义为
分数阶Newton-Leipnik混沌系统[4]为
(1)
当μ1=0.4,μ2=0.175,α∈[0.989,1]时, 系统(1)出现奇异吸引子. 以系统(1)作为驱动系统, 设计响应系统为
(2)
定义误差
e1=x2-x1,e2=y2-y1,e3=z2-z1,
将式(1)与式(2)相减可得
(3)
1 滑模同步
假设条件:
(H1) |e2+10(y2z2-y1z1)|<ε1|e1|,ε1<μ1;
(H2) |-e1+5(x2z2-x1z1)|<ε2|e2|,ε2<0.4;
(H3)x1,y2为有界变量, 即存在正常数M>0, 满足|x1| 则分数阶系统(1)渐近稳定. 则分数阶Newton-Leipnik主从系统(1)和(2)取得滑模同步. 证明: 在滑模面上运动时, 根据误差系统方程(3)可得 构造函数 构造函数 由(H2)可得 再由 可得 又由于e1→0,e2→0, 且在滑模面上s=0, 因此可得误差方程 由(H1)易得 -ε1|e1| 从而有 -ε1|e1|+e2<-10(y2z2-y1z1)<ε1|e1|+e2. 同理由(H2) 易得 -ε2|e2|-e1<-5(x2z2-x1z1)<ε2|e2|-e1, 从而可得 -ε1|e1|+e2-ε2|e2|-e1<-5(x2z2-x1z1)-10(y2z2-y1z1)<ε1|e1|+e2+ε2|e2|-e1. 又由于e1→0,e2→0, 因此由两边加定理易得 -5(x2z2-x1z1)-10(y2z2-y1z1)→0, 从而 不在滑模面上运动时, 构造Lyapunov函数V(t)=s2/2, 求导可得 因此s(t)是可积的且有界, 由引理2可知,s(t)→0. 定理2在假设条件(H1)~(H3)成立下, 选取 控制器 u(t)=-(k+μ2)e3(t)-ηsgn(s(t)),k>0 为常数, 则分数阶Newton-Leipnik系统的主从系统(1)和(2)可取得比例积分滑模同步. 证明: 将等效控制器代入式(3)可得理想滑模方程为 (4) 在滑模面上运动时, 根据误差系统方程(3)可得 构造函数 -5(x2y2-x1y1)=-5(x2-x1)y2-5x1(y2-y1)=-5e1y2-5x1e2. 当不在滑模面上运动时, 选取Lyapunov函数V(t)=s2/2, 求导可得 根据引理2可知,s(t)→0. 选取系统参数μ1=0.4,μ2=0.175,α=0.93, 设置系统初始值为 (x1(0),y1(0),z1(0))=(2,1,3), (x2(0),y2(0),z2(0))=(1,2,2), 分别采用定理1和定理2中的滑模面和控制器进行数值仿真, 定理1和定理2的系统误差曲线分别如图1和图2所示. 由图1和图2可见, 开始时误差相差较大, 随着时间的延长, 系统误差逐渐趋于一致. 定理1中当时间t>0.275 s后, 系统取得滑模同步, 定理2中当t>0.225 s后, 系统取得比例积分滑模同步. 显然, 定理2比定理1中的控制器简单且能在更短时间内达到同步. 图1 定理1的系统误差曲线Fig.1 System error curves of theorem 1 图2 定理2的系统误差曲线Fig.2 System error curves of theorem 2 综上, 本文研究了分数阶Newton-Leipnik混沌系统的滑模同步问题, 设计了滑模面和控制器, 并给出了系统取得同步的充分性条件, 最后通过数值算例验证了该方法的可行性与有效性.


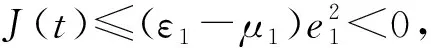

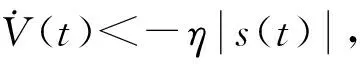
2 比例积分滑模同步
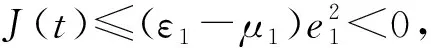

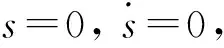
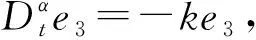
3 数值仿真