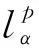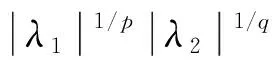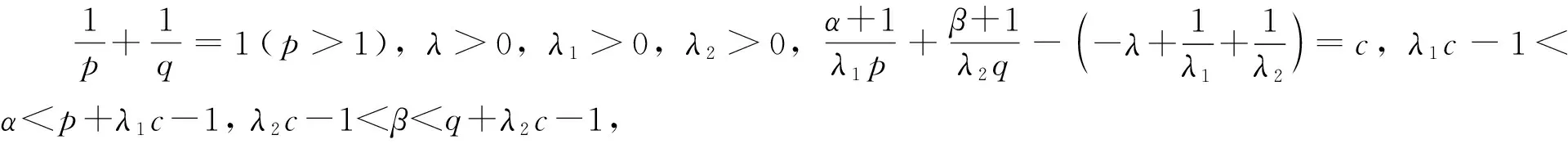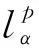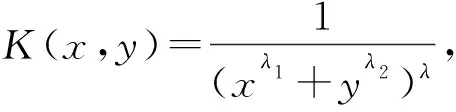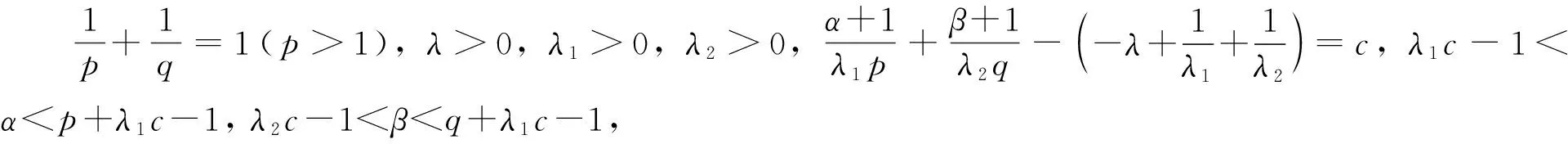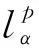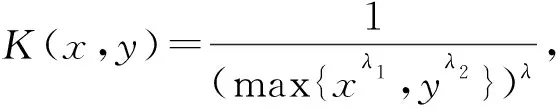一类准齐次核的Hilbert型级数 不等式成立的充要条件及应用
2018-11-06曾志红
洪 勇, 曾志红
(1. 广东财经大学 统计与数学学院, 广州 510320; 2. 广东第二师范学院 学报编辑部, 广州 510303)
1 引言与预备知识
目前, 关于Hilbert型不等式的研究已有很多结果[1-11]. 设p>0,α是常数, 定义空间
(1)
为Hilbert型级数不等式. 不等式(1)可等价地化为
(2)

(3)
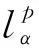
为T的(p,p)型算子范数.
定义1设λ,λ1,λ2为常数,t>0, 若K(x,y)满足
K(tx,y)=tλλ1K(x,t-λ1/λ2y),K(x,ty)=tλλ2K(t-λ2/λ1x,y),
则称K(x,y)为具有参数(λ,λ1,λ2)的准齐次函数.

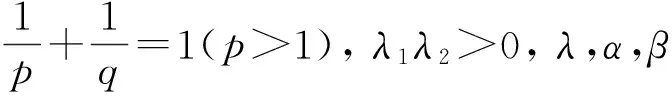
证明: 由于K(x,y)是具有参数(λ,λ1,λ2)的准齐次函数, 且由
可得
因此有
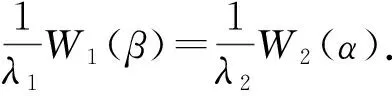
同理可得ω1(m,β)≤mλλ1-(λ1/λ2)((β+1)/q-1)W1(β).
2 主要结果
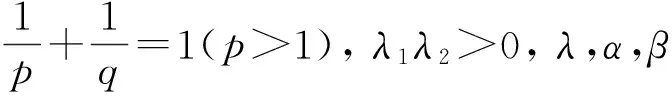
K(x,y)≥0是具有参数(λ,λ1,λ2)的准齐次可测函数,s+r=1(0 均收敛. 则: (4) 2) 若M0是式(4)的最佳常数因子, 则 当c=0时, 有 证明: 1) 设式(4)成立. 若λ1c<0,λ2c<0, 取am=m(-α-1+λ1cps)/p,bn=n(-β-1+λ2cqr)/q, 则有 由式(4)~(6), 得 (7) 从而可得 (8) 2) 首先由式(8)可知 当c=0时, 式(8)可化为 (9) 对足够小的ε>0, 取am=m(-α-1-|λ1|ε)/p(m=1,2,…),bn=n(-β-1-|λ2|ε)/q(n=1,2,…), 则有 对足够小的δ>0, 存在N, 使得n>N时, 有n-λ2/λ1<δ. 记 则有 由式(9)~(11), 可得 令ε→0+, 得 于是有 再令δ→0+, 得 由于式(1)与式(2)等价, 因此由定理1可得: 定理2设算子T由式(3)定义, 则在与定理1相同的条件下, 有: 2)T的(p,p)型算子范数满足 当c=0时, 有 则: 2) 当c=0时,T的(p,p)型范数为 当c=0时, 则: 2) 当c=0时,T的(p,p)型范数为 当c=0时,
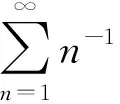



3 应 用