动态经济中的次优公共资本积累与所得税结构1
2018-11-05金戈朱丹
金戈 朱丹
0 引言
公共投资及其积累而成的公共资本在世界各国的经济发展中扮演了极为重要的角色。那么,在一个动态经济中,一国政府应该遵循什么样的规则来制定其公共投资政策?应该将公共资本与私人资本之间的比例保持在何种水平?特别地,当政府无法征收总额税,只能以所得税这样的扭曲税为公共投资进行筹资时,税收扭曲会对最优公共投资规则以及最优公共—私人资本比例产生什么影响呢?对这些问题的探索,具有重要的理论与政策意义。
对于公共投资与经济增长这一主题的理论研究早在20世纪70年代初就开始了。Arrow and Kurz(1970)首先在新古典外生经济增长的框架里对上述问题进行了开创性研究。Barro(1990)则进一步在一个内生经济增长模型中对最优公共投资进行了突破性研究并带动了大量后续文献。需要指出,为了方便处理,Barro及其后续文献(如Turnovsky,2000)大多采用了相对简单的模型设定方式,即假定生产性公共服务以流量的形式影响经济。
然而,正如Futagami et al.(1993)所言,实践中大多数公共基础设施(如高速公路、机场、港口、电力设施等)均以存量的形式存在(由于这篇文献在本文中出现的频率较高,为了书写方便,以下简称FMS,1993。)而且,大量经验研究(如Aschauer,1989)表明公共资本具有较强的生产性,并且公共资本提高了私人资本的生产性。从而,在模型中假定公共投资以累积为存量的形式(即公共资本)影响经济是更为合理的。
基于上述考虑,FMS(1993)、Greiner and Haunch(1998)、Turnovsky(1997,2004)、Gomez(2004,2008)、Tamai(2008)、Chatterjee and Ghosh(2011)、Economides et al.(2011)(由于这篇文献在本文中出现的频率也较高,以下简称EPP,2011)、Misch et al.(2011,2013)等众多文献围绕着公共资本与经济增长这一主题展开了深入研究,包括最优公共资本积累、拥挤性、折旧与维修、转移动态等一系列问题。
值得注意的是,现有关于最优公共资本的研究文献往往假定政府以总额税,或类似于总额税的税收结构为公共支出筹资。众所周知,总额税是没有扭曲性的,因而这些文献得到的结果也是社会最优的(如Turnovsky,1997;Chatterjee and Ghosh,2011)。
问题在于,在现实世界中,总额税是很难实施的。因此,有大量研究动态最优税收的理论文献排除了总额税,转而假定政府以扭曲性的收入税筹资,考察了次优财政政策问题。[注]这里需要指出,在研究最优财政政策或最优税收的文献里,一般区分两种程度的最优,分别是:第一级最优(the first-best optimal),简称第一优;第二级最优(the second-best optimal),简称次优。然而,这一系列的文献或者假定公共支出外生(Chamley,1986;Judd,1985;Lucas,1990;Chari et al.,1991,1994;Atkeson et al.,1999;Erosa and Gervais,2002;Farhi,2010;Staub and Werning,2014),或者假定公共支出以流量的形式影响经济(Barro,1990;Judd,1999;Park and Philippopoulos,2002;Chen,2006;Gomez,2014)。此外,有一类研究次优税收与公共资本的文献(如Glomm and Ravikumar,1994;Lau,1995,Devarajan et al.,1998)虽然在模型中引入了公共资本,但这些文献假定公共资本完全折旧,也就是本期的公共资本在当期末全部消耗,只有本期公共投资进入下一期,成为下一期公共资本,因此,这一类文献并没有研究公共资本的积累问题,其本质和假定公共支出以流量形式影响经济的文献相同,研究结论也相似。[注]在Barro(1990)的模型中,公共投资以流量形式影响当期经济,最优公共投资占产出的比例等于公共服务的产出弹性。在Glomm and Ravikumar(1994)、Lau(1995)和Devarajan et al.(1998)的模型中,本期公共投资转化为下一期公共资本,因此,最优公共投资占产出的比例等于公共资本的产出弹性乘以一个折现因子。
在动态最优公共资本积累的研究领域,只有FMS(1993)、EPP(2011)等少数文献在政府以收入税筹资的模式下考察了次优公共资本积累问题。其中,FMS(1993)是这一领域的经典文献,提出了一个标准的研究次优公共资本积累的内生经济增长模型。FMS沿用了Barro(1990)的研究方法,得到了两个重要的基本结论:
(1) 为使经济增长率达到最大化,收入税率应该等于公共资本的产出弹性(FMS,1993,命题3)。
(2) 为使社会福利达到最大化,最优收入税率应该小于增长率最大化的收入税率(即小于公共资本的产出弹性)(FMS,1993,命题5)。
但是,FMS(1993)也遗留了三个非常重要的问题有待解决:
首先,FMS没有说明最优收入税率的表达式究竟应该如何决定。由于在FMS的框架里,公共投资占产出的比例等于收入税率,因此,FMS未能给出关于收入税筹资模式下的次优公共投资规模(相对产出)的表达式。
其次,FMS没有得到次优公共资本积累规则。
第三,FMS也没有说明,在次优平衡增长路径上,公共资本与私人资本之间的比例关系应该如何决定。
FMS(1993)遗留的这些问题至今未能在次优框架内得到满意地解决。EPP(2011)试图求解次优公共资本和公共投资问题,但由于他们使用的研究方法较为复杂,因此也没有给出关于次优公共资本积累的定性结论,只是得到了一些数值结果。由于这些数值结果过于依赖参数取值,因而仅仅有数值结果,从理论研究的角度来说是不够的。此外,由于FMS(1993)和EPP(2011)都假定劳动供给是无弹性的,从而劳动收入退化,因此,他们也都没有讨论有关资本所得税与劳动所得税之间的结构问题。
本文在FMS(1993)和EPP(2011)的基础上,旨在进一步深入考察次优配置中的最优公共资本积累规则以及相应的最优所得税结构,并希望对FMS所遗留的三个重要问题给出较为明确的定性结论。为此,本文在FMS模型基础上构建了一个包含公共资本积累与弹性劳动供给的内生经济增长模型,在简要考察社会最优配置以提供参照系的基础上,本文重点分析了政府以收入税筹资下的次优配置。由于本文引入了弹性劳动供给,这使得我们可以将收入税区分为资本所得税和劳动所得税。同时本文也排除了使用总额税筹资的可能性。针对FMS(1993)所遗留的问题,本文所提出的核心问题是:
(1) 在政府以扭曲性的资本税和劳动税筹资的模式下,次优公共资本积累规则是怎样的?
(2) 如何确定所得税筹资模式下的次优公共投资规模?
(3) 次优路径上,公共资本与私人资本之间应该保持怎样的比例?
(4) 次优配置与社会最优配置之间又存在着什么差异?
为了能够回答上述问题,并给出较为明确的定性结论,我们需要采用一种更为简便、容易处理的方法。FMS(1993)使用了Barro(1990)的研究方法,即得到社会福利函数的表达式后,利用社会福利对税率求导推出最优税率。EPP(2011)则采用了标准的拉姆齐方法,采取两阶段求解,首先得到消费者的一阶条件,然后将消费者的所有一阶条件和约束条件作为政府问题的约束条件,求解政府问题的最优解。但这两种方法都过于复杂,无法得到明确的定性结论。为此,本文采用对偶方法(the dual approach),本质上是一种逆向归纳方法,即首先得到消费者对政策参数的反应函数,再将其代入政府问题求解最优税率与公共投资。在最优税收领域,该方法最早由Diamond and Mirrlees(1971)运用于静态模型,并被Chamley(1986)和金戈(2010)运用于动态模型。
与现有研究文献相比,本文的主要贡献和结论体现在以下两个方面:
首先,本文运用对偶方法(逆向归纳方法),对政府以收入税筹资模式下的次优公共资本积累问题进行了理论分析,得到了具有一般性意义的最优公共资本积累规则。这一规则表明:在收入税筹资模式下,沿着平衡增长路径,次优公共资本积累应该使得最后一单位公共资本的边际产出等于私人资本的税后收益率。进一步,我们将这一次优公共资本积累规则与社会最优(第一优)规则进行了比较。在社会最优配置下,第一优公共资本积累规则要求公共资本的边际产出等于私人资本的边际产出;而在次优配置下,给定资本税率为正,则次优公共资本积累要求公共资本的边际产出小于私人资本的边际产出。这一差异背后的经济学含义是,由于资本税使得私人资本的边际产出(即税前收益率)与税后收益率之间形成了一个楔子,而最后一单位公共资本的边际收益应该根据私人资本的税后收益率来确定,从而公共资本的边际产出与私人资本的边际产出之间存在一个税收楔子(tax wedge)。相应地,我们还得到了次优公共投资规模(相对于产出的比例)及次优公共资本—私人资本比例等一系列重要结果,并将这些结果与社会最优配置进行了比较,得到了一些有意义的发现。
其次,本文在上述研究文献的基础上,引入了弹性劳动供给,考察了平衡预算规则下的次优资本所得税和劳动所得税结构。在本文的理论分析中,我们给出了一组决定次优税率的公式,并验证了平衡预算规则。进一步,我们通过参数赋值和数值计算,给出了不同参数赋值下的第一优与次优公共投资以及次优税率等一系列变量的数值解。结果表明,在合理的参数赋值下,次优资本税率和劳动税率均为正。
本文余下内容安排如下:第1部分介绍本文的模型设定。第2部分在命令经济中考察了社会最优配置,以此作为参照系。本文的核心贡献主要在第3部分,我们在一个政府以资本所得税和劳动所得税筹资的分散经济中研究次优均衡配置,给出了平衡增长路径上的次优公共资本积累规则,并与第一优配置进行了比较;同时,我们还分析了次优资本税和劳动税的结构。第4部分在前面两个部分的研究基础上,进行参数赋值和数值计算,给出了模型数值解,并探讨了某些核心参数的变动对各变量最优解的影响。最后一个部分对全文进行简短的总结。
1 模型
本文的模型建立在FMS(1993)等人的研究基础上,但我们引入了弹性劳动供给。假定代表性消费者的跨期效用函数形式为:

(1)
其中,c(t)和l(t)分别表示t期的人均私人消费和劳动。标准化消费者在每期的总时间禀赋为1,则(1-l(t))表示消费者在t期的闲暇。ρ>0为消费者的时间偏好参数。我们参照Park and Philippopoulos(2002)以及EPP(2011)等文献的设定,假定瞬时效用函数u(c,1-l)具有对数形式,即
u(c,1-l)=lnc+βln(1-l)
(2)
其中,β>0,表示消费者对闲暇的偏好强度。[注]为了将研究重心集中于最优公共资本积累问题,我们在效用函数中忽略了消费性公共服务。这是一种简化,但不会对本文的结论产生实质性影响。我们可以很容易将消费性公共支出引入效用函数并推导出最优消费性公共支出的规则和相应比例,但这不会影响本文关于最优公共资本积累的一系列结论。
代表性企业的生产函数为:
y(t)=f(k(t),l(t),kg(t))
(3)
其中,k(t)和kg(t)分别为t期的人均私人资本和人均公共资本。这里,我们引入了FMS(1993)等文献的核心假定,即假定生产性公共服务以存量形式(即公共资本)进入生产函数。参照通行的做法,我们假定生产函数具有柯布—道格拉斯形式,即
(4)
其中,α∈(0,1)表示公共资本的产出弹性。相应地,私人资本产出弹性为(1-α)。给定公共资本数量不变,我们假定生产技术对劳动和私人资本是规模报酬不变的,这是新古典生产函数的一个基本假定。给定劳动水平不变,则生产函数对私人资本和公共资本也具有一次齐次性质,这实际上是Barro(1990)和FMS(1993)模型的基本假定。因此,该生产函数集合了Barro生产函数和新古典生产函数的一些共同特征。
假定初始私人资本k(0)=k0,初始公共资本kg(0)=kg0。为了方便,我们还假定私人资本和公共资本均没有折旧。[注]如果引入一个正的折旧率δ(0<δ<1),不会对本文的结论产生实质影响。
政府通过生产性公共资本向社会公众提供生产性公共服务。参照Barro(1990)、FMS(1993)等文献的处理方法,我们假定公共服务以人均形式进入生产函数。人均公共资本kg的积累方程为:
(5)
其中,gI(t)为人均生产性公共支出(公共投资)。
从而,人均意义上的社会资源约束(即私人资本的积累方程)为
(6)
这样,我们就完成了对模型的描述。
2 社会最优配置
我们首先在命令经济中考察社会最优配置(第一优配置),并以此作为一个参照系。有关所得税筹资模式下的分散均衡配置及次优财政政策问题将在第四部分展开。
在命令经济中,我们假定政府全知全能,能够直接配置各种变量。这样,以社会福利最大化为目标的政府所面临的问题就是:在社会资源约束式(6)、公共资本积累方程式(5)以及初始的公共及私人资本约束下,通过直接选择人均消费、劳动以及公共投资的动态路径,以最大化代表性消费者的跨期效用式(1)。
该问题的汉密尔顿函数为:
H(c,l,gI;θ,μ)=lnc+βln(1-l)+θ(y-c-gI)+μgI
(7)
其中,θ和μ分别为私人资本和公共资本的社会边际价值。
关于人均消费、劳动和公共投资三个变量的一阶条件分别为:
式(10)意味着,在社会最优路径上,最后一单位公共投资应使得公共资本的社会边际价值等于私人资本的社会边际价值。
进一步,关于两个汉密尔顿乘子的运动方程分别为:
其中,fk和fkg分别为生产函数f(k,l,kg)对k和kg的偏导数。将式(10)代入以上两式,我们可以得到:
(13)
式(13)给出了社会最优路径上的公共资本积累规则,即最后一单位公共资本的边际产出应等于最后一单位私人资本的边际产出。
我们将上述结论总结为命题1。
命题1(社会最优公共资本积累规则)
在社会最优路径上,公共资本的边际产出等于私人资本的边际产出。
命题1的经济含义是显而易见的:当经济沿着社会最优路径增长时,最后一单位公共投资的边际收益(公共资本的边际产出)应该等于其边际机会成本(相当于投资于私人资本的边际产出);换句话说,最后一单位投资,无论投资于公共资本,还是私人资本,所带来的边际产出应该相等,否则就应该调整两种资本的结构直至两者的边际产出相等。
需要指出,命题1的结论在Arrow and Kurz(1970)、Turnovsky(1997)和Tamai(2008)等文献中以不同形式出现,这里只是将其以一种更为简洁的形式呈现出来。本文的核心理论贡献主要在第3部分。
进一步,在柯布—道格拉斯生产技术下,由于fk=(1-α)y/k,fkg=αy/kg,利用式(13),我们可以得到:

(14)

上述结论归纳为命题1的推论。
命题1的推论(社会最优公私资本比)
在柯布—道格拉斯生产技术下,社会最优的公共资本与私人资本的比例等于其产出弹性之比。
进一步,结合式(8)和式(12),我们得到:
(15)
其中,γ表示增长率,上标1st表示第一优(the first-best optimal)配置。上式是社会最优路径的欧拉方程,它给出了社会最优的消费增长率。

我们利用公共资本积累方程式(5)和生产函数式(4),得到:
(16)
联立式(15)和式(16),我们得到:
(17)
式(17)的结论非常重要,我们将其作为一个命题。
命题2(社会最优公共投资规模)
众所周知,如果生产性公共服务以流量形式影响经济,则最优生产性公共支出与产出的比例等于生产性公共服务的产出弹性,即(gI/y)1s t=α。但是,当生产性公共服务以存量形式(即公共资本)影响经济时,命题2告诉我们,最优公共投资与产出的比例应该小于公共资本的产出弹性,即(gI/y)1s t<α。
上述结论可以这样来理解:当公共支出以流量形式影响经济时,过去的公共支出已经消耗,对本期的生产是没有价值的;而当过去的公共投资形成存量,并与本期的公共投资结合为本期的公共资本影响生产时,过去的公共支出对本期的生产具有累积效应。两者相比,如果在第二种情形中,公共支出占产出的比例仍然等于α,显然是一种浪费。因此,在公共支出以存量形式影响生产时,公共支出与产出的最优比例必然应该小于α。
进一步,利用平衡增长时消费增长率等于私人资本增长率这一特征,我们结合式(6)和式(15),得到:
(18)
再利用式(17),我们得到平衡增长路径上的最优私人消费—私人资本比例:
(19)
最后,我们将一阶条件式(8)代入式(9),再利用式(19),得到如下方程:
(20)
3 分散均衡配置与次优财政政策
在分散经济中,行为人根据既定的政策参数作出最大化决策。如果政府可以用总额税为公共投资筹资,并根据公共投资的社会最优规则设定公共资本与私人资本的比例,则分散经济可以实现社会最优配置。但这种情形只存在于理想世界中。一般而言,现实中政府很难征收总额税或类似的非扭曲性税收,而只能代之以扭曲税进行筹资,相应的最优配置实际为次优(the second-best optimal)配置。考虑到这一事实,大量文献(如Chamley,1986;Lucas,1990;Atkeson et al.,1999;Farhi,2010;Straub and Werning,2014)致力于研究次优税收问题。在最优公共资本积累研究领域,FMS(1993)和EPP(2011)等少数文献也重点考察了政府以扭曲性的所得税(即收入税income tax)筹资的情形。
本文沿着FMS(1993)、EPP(2011)的思路,假定政府以所得税为公共投资筹资。但与他们假定只有一种(资本)所得税的处理方法不同,我们引入了弹性劳动供给,因此,将所得税区分为劳动所得税和资本所得税。这使得我们可以重点考察次优配置中的所得税结构。
假定政府实行平衡预算政策,其预算约束为:
(21)

这样,消费者面临的预算约束为

(22)

3.1 消费者的反应函数
在第二阶段,消费者的跨期效用最大化问题就是在预算约束式(22)和初始资本条件下,通过选择人均消费和人均劳动(闲暇),最大化跨期效用函数式(1),其汉密尔顿函数为:

(23)
其中,q为汉密尔顿乘子。
关于控制变量c,l的一阶条件分别为:
q的运动方程为:

(26)
根据式(24)和式(26),我们得到:
(27)
下面我们重点考察平衡增长路径。沿着平衡路径,消费和资本等变量以同样的不变速率增长。这样,我们结合式(27)和式(22),得到:

(28)
利用式(24)、(25)和(28),我们不难得到:

相应地,消费者在平衡路径上的(瞬时)间接效用函数为:

(31)
3.2 政府的次优财政政策
在平衡增长路径上,政府的最大化问题是在社会资源约束式(6)、公共资本积累方程式(5)、政府预算约束式(21),以及初始资本的约束下,通过选择次优政策变量使得消费者的跨期(间接)效用最大化。
这样,政府的汉密尔顿函数为:
(32)

vk=0⟹v=0
(33)

(34)

(35)
关于公共投资的一阶条件为:
φ=λ
(36)
通过比较式(36)与式(10),我们发现,在所得税筹资模式下的次优公共资本积累与社会最优公共资本积累应满足的一阶条件是一致的,即在任意时刻,最后一单位公共投资应使得公共资本的边际社会价值应等于私人资本的边际社会价值。
但上述发现并不意味着在次优路径上,公共资本和私人资本的边际产出必然相等。实际上,一般而言,两者是不相等的。为了看清这一点,首先我们推导出公共资本的边际社会价值(乘子φ)的运动方程为:
(37)
在平衡增长路径上,乘子φ、λ和q以相同的速度变动,结合式(36)、(37)和(26),我们得到:
(38)
其中,上标2nd表示次优(the second-best optimal)配置。上式给出了次优平衡增长路径上的最优公共资本积累规则。这一规则告诉我们,在以所得税筹资的次优配置中,沿着次优的平衡增长路径,公共资本的边际产出应该等于私人资本的税后收益率。我们将这一结论概括为一个命题。
命题3(次优公共资本积累规则)
在以所有税筹资的分散均衡配置中,沿着次优平衡增长路径,公共资本的边际产出等于私人资本的税后收益率。
命题3是本文的第一个核心结论,其经济含义将与后文给出的命题3推论一起讨论。进一步,利用式(35)的结果,我们可以得到λ的运动方程为:
(39)
由于在平衡增长路径上,c和kg同比例增长,利用式(27)、(38)和(5),得到:
(40)

命题4(次优公共投资规模)

命题4是本文的第二个核心结论,给出了次优平衡增长路径上的最优公共投资规模(相对于产出)。通过比较命题4与命题2,我们可以发现次优与社会最优的公共投资—产出比具有相同的结构,因此,(gI/y)2nd也必然小于公共资本的产出弹性α。
根据式(27)和式(38),可知,在次优平衡增长路径上,经济增长率为:
(41)
下面,我们考察次优所得税结构。由于λ和q同比例变动,利用式(39)、(26)和(38),得到:
(42)
进一步,利用式(24)、(39)和(6),得到:
(43)
将式(40)代入式(43),得到:
(44)
我们将式(29)和式(44)代入式(42),得到资本所得税楔子为:
(45)
同时,利用一阶条件式(30),可以得到相应的劳动所得税楔子为:
(46)
根据式(45)和式(46),不难得到次优平衡增长路径上的资本税额与劳动税额,分别为:
注意,式(47)、(48)给出了次优所得税结构。下面,我们来验证预算平衡规则。加总以上两式,易得:
(49)
根据式(40),我们得到:
(50)
这样,我们就验证了平衡预算。

这样,根据式(38),我们立即发现:次优平衡路径上,公共资本的边际产出应该小于私人资本的边际产出。我们将这一发现总结为命题3的推论1。
命题3的推论1(次优公共资本积累规则)
在以所有税筹资的分散均衡配置中,给定资本税率为正,则沿着次优平衡增长路径,公共资本的边际产出小于私人资本的边际产出。
命题3及其推论1给出了次优公共资本积累规则,是本文最重要的结论之一。通过将命题3及其推论1与命题1的结论进行比较,我们可以得到一个非常重要的发现:即在社会最优路径上和次优平衡增长路径上,公共资本的积累规则是不同的。前者要求公共资本的边际产出等于私人资本的边际产出,后者则要求公共资本的边际产出等于私人资本的税后收益率。给定资本税率为正,则公共资本的边际产出应小于私人资本的边际产出。归根到底,这是因为资本税使得私人资本的边际产出(即税前收益率)与税后收益率之间出现了一个税收楔子,而公共资本的边际产出应该根据私人资本的税后收益率来确定,从而公共资本与私人资本的边际产出之间也存在一个税收楔子。
进一步,通过比较式(51)和(45),可知,给定资本税大于0,则必然有:
(53)
我们将上述结论总结为命题3的推论2。
命题3的推论2(次优公私资本比)
在以所有税筹资的分散均衡配置中,给定资本税率为正,则在柯布—道格拉斯生产技术下,沿着次优平衡增长路径,公共资本与私人资本的比例大于其产出弹性之比。
命题3的推论2是本文的第三个重要结论,给出了次优平衡增长路径上公共资本与私人资本的比例关系。对比命题1的推论,不难发现,由于公共资本的边际产出小于私人资本的边际产出,这使得次优配置中的公共资本与私人资本的比例大于社会最优配置中的公共资本—私人资本比。
进一步,我们来比较(c/k)2nd与(c/k)1st的关系。由于(c/k)2nd=1/(qk),给定资本税为正,在次优配置中,资本的边际私人价值q必然小于资本的社会边际价值λ,则根据式(24)、(44)、(53)和(19),必然有:
(54)
上式意味着,在次优配置中,个体将选择更高的私人消费—资本比。
为了比较次优经济增长率与社会最优经济增长率的关系,我们需要借助于比较次优路径上的资本社会边际价值λ与社会最优路径上的资本社会边际价值θ的关系。根据式(44)、(53),(19)和(8),我们得到:
(55)
由于社会最优路径上的资本社会价值大于次优路径上的资本社会价值,且资本税为正,则必然有:
(56)
从而,我们得到:
γ2nd<γ1st
(57)

最后,根据式(17)和(40),得到:
(58)
也就是说,次优路径上政府也将选择一个相对更小的公共投资—产出比。
这样,我们在给定资本税率为正的前提下,比较了次优平衡增长路径与社会最优平衡增长路径的关系。与社会最优路径相比,沿着次优平衡增长路径,经济具有以下特征:
(1) 消费者将选择更高的私人消费—资本比和更少的劳动供给;
(2) 政府将选择更低的公共投资规模(以占产出的比例衡量);
(3) 政府将选择更高的公共资本—私人资本比例,使得公共资本边际产出低于私人资本边际产出(两者之间相差一个税收楔子)。
(4) 次优经济增长率低于社会最优经济增长率。
4 数值计算
为了进一步比较第一优与次优配置的差异,考察第一优与次优公共资本积累以及次优所得税结构的数量特征,分析参数变动对最优财政政策和消费者选择的影响,下面我们进行数值分析。
关于偏好方面的参数,我们参照Turnovsky(2000),设时间偏好参数ρ=0.04。为了考察消费者对闲暇的偏好变动如何影响消费者和政府的选择,我们设闲暇偏好参数β∈{0.3,0.5}。
至于生产方面的参数,我们设技术系数A=0.25。同样,为了考察公共资本生产能力的变动如何影响最优财政政策,我们设公共资本产出弹性系数α∈{0.2,0.3,0.4}。
数值计算过程简要说明如下:社会最优配置的数值解主要基于方程式(4)、(14)、(15)、(19)和(20)计算得到。次优配置的数值解主要基于方程式(4)、(29)、(40)、(41)、(45)、(46)、(51)和(52)计算得到。数值计算结果如表1和表2所示。

表1 数值结果(1)
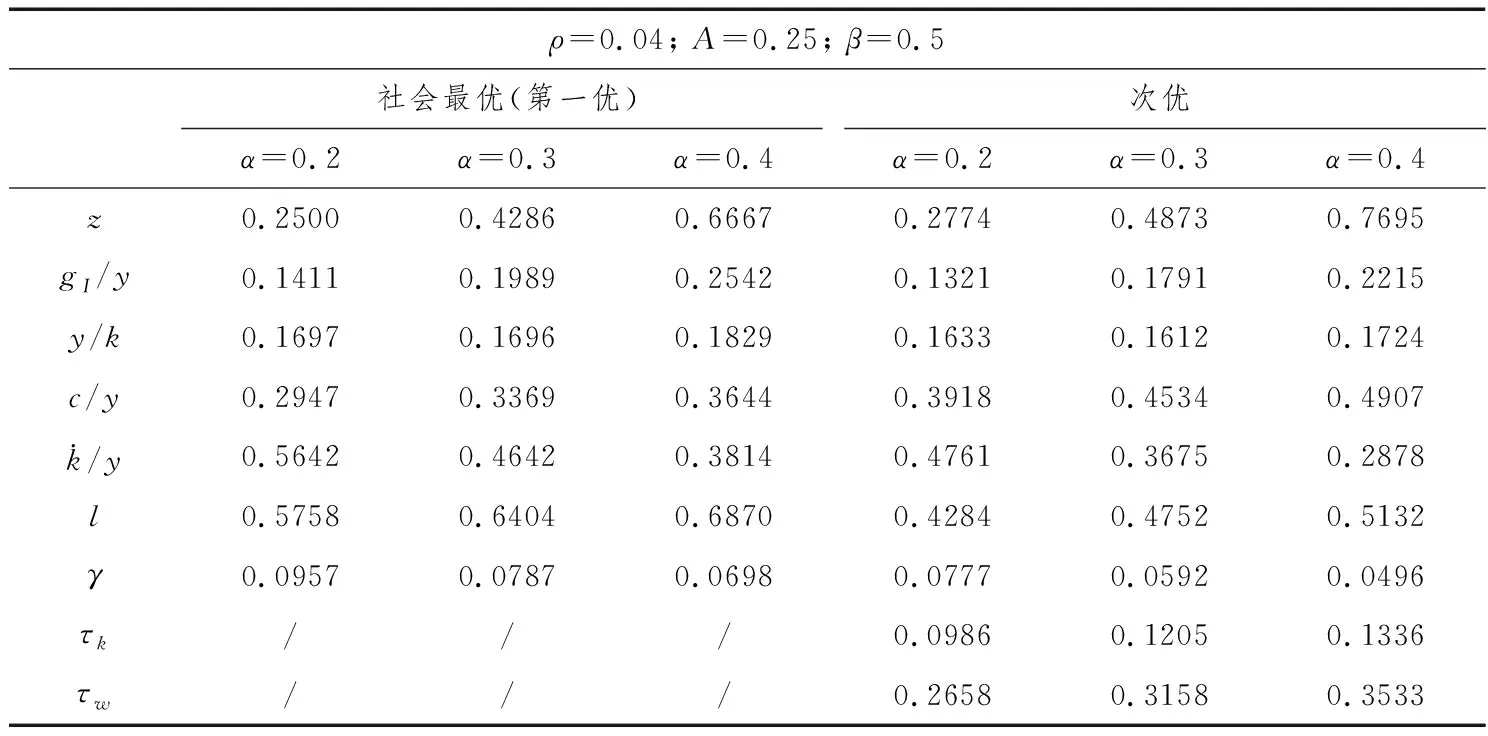
表2 数值结果(2)

首先,我们观察到,在任意一种情形中,给定参数不变,相比社会最优配置,在次优平衡增长路径上,消费者选择了更高的消费(相对于产出的比例)和更低的劳动供给,政府则选择了更低的公共投资(相对于产出),其结果是在次优配置中形成了更高的公私资本比和更低的经济增长率。此外,要注意到,在上述六种情形中,政府都选择了正的资本税率和劳动税率。这些定量分析结果均印证了我们在上一部分定性分析中得到的结论。进一步,我们还可以得到一些重要的比较静态结果:
(1) 给定其他参数不变,随着公共资本产出弹性系数α(同时也是劳动的产出弹性系数)上升,无论是沿着社会最优平衡路径还是次优平衡路径,公共投资和私人消费(相对于产出)以及劳动供给均将上升,私人投资(相对于产出)将下降;与此同时,经济增长率将出现下降。
(2) 给定其他参数不变,随着闲暇偏好参数β上升,则不管在社会最优配置中还是次优配置中,消费(相对于产出)将上升,劳动供给以及公共投资和私人投资(相对于产出)将下降,与此同时,经济增长率也将下降。
以上两个结果从经济学直觉上也是很容易理解的。首先,公共资本的产出弹性系数相对提高,而私人资本的产出弹性相对下降,要求社会增加对公共资本的投资并减少对私人资本的投资;与此同时,劳动的边际产出提高导致消费者愿意提供更多数量的劳动供给并获得更高的劳动收入,进一步,消费者将增加的收入用于增加私人消费支出。其次,对闲暇的偏好参数提高,这本质上是一种马斯洛意义上的需求层次提高,从而公众倾向于增加闲暇时间和私人消费支出;同时劳动时间、公共和私人投资水平则相应减少。这个结果也为现实中发达国家和发展中国家之间的一些特征事实差异提供了一种解释。
5 结论
本文构建了一个包含公共资本积累和弹性劳动供给的内生经济增长模型,在政府以资本所得税和劳动所得税两种扭曲税筹资的模式下,重点考察了次优公共资本积累规则、次优公共投资规模以及相应的次优税收结构等一系列问题,并将次优配置与社会最优配置进行了比较。
我们发现,沿着次优平衡增长路径,次优公共资本积累规则要求最后一单位公共资本的边际产出等于私人资本的税后收益率。因此,给定资本税率为正(由于政府受到平衡预算规则的约束,在合理的参数范围内,资本税率为正),次优公共资本的边际产出小于私人资本的边际产出(相差一个税收楔子)。相比之下,社会最优配置要求两者相等。显然,这是因为扭曲税导致了最优公共资本积累规则的改变。进一步,如果生产函数具有柯布—道格拉斯形式,则次优的公共资本—私人资本比例将大于两种资本的产出弹性之比;而社会最优配置要求两者相等。我们还发现,次优的公共投资规模(相对于产出的比例)小于社会最优公共投资规模,而后者又小于公共资本的产出弹性。
我们还给出了一组决定次优资本税率与劳动税率的公式。尽管无法在定性分析中给出次优税率的显式解,但验证了次优税率和次优公共支出确实能够保证平衡预算约束的成立。进一步,我们在数值计算中,得到了六种情形的数值解。这些数值结果表明,在合理的参数范围内,次优资本税率与劳动税率均为正。
我们的数值研究还表明:给定其他参数不变,随着公共资本产出弹性上升,公共投资和私人消费(相对产出的比例)以及劳动供给均将上升,私人投资和经济增长率则将下降;而随着闲暇偏好参数的上升,消费将上升,劳动供给以及公共和私人投资将下降,经济增长率也将下降。
本文的理论研究为实践中的公共投资政策提供了一些重要的理论启示。特别地,本文的研究表明,政府在制定最优公共投资政策时应当考虑税收对最优公共投资的影响。传统的研究成果一般都认为政府在制定最优公共投资政策时应该使得公共资本和私人资本的边际产出保持一致。本文则发现,当政府以扭曲税为公共投资筹资时,在制定政策时不应再追求公共资本与私人资本的边际产出相等,而应该使得两者之间相差一个税收楔子;换句话说,最优投资应使得公共资本的边际产出等于私人资本的税后收益。另外,对于大国而言,不同地区之间的公共资本产出弹性以及消费者对闲暇的偏好都会存在较大的差异,因此,不适宜由中央政府来统一制定全国的公共投资政策,而应由各地政府根据本地实际情况因地制宜地来制定适于各个地区的公共投资政策。
需要指出,本文的模型没有考虑公共资本的拥挤性。一般而言,当模型中引入公共资本的拥挤性后,扭曲性税收具有矫正私人部门行为外部性的作用,因此,这一类模型往往能够得到一个社会最优的结果(如Turnovsky,1997)。在本文的研究基础上,我们可以进一步拓展模型,假定公共资本具有多种类型,不同类型的公共资本具有不同程度的拥挤性(从无拥挤性到具有高度拥挤性),这样我们可以对最优公共资本问题和最优税收问题作出更深入的分析。
