GM(1,1)模型的优化及其在乙肝发病预测中的应用研究*

潍坊医学院(261053)

许小珊 孙 娜 杜彦春 李望晨 王素珍△ 石福艳△

【提 要】 目的 通过对传统GM(1,1)模型优化,并探讨优化后的GM(1,1)在乙肝发病预测中的应用,为乙肝防治提供科学依据。方法 对传统GM(1,1)建模的维数、背景值和初始值进行改进,通过比较不同模型对2007-2017年全国乙肝发病率数据拟合效果,选择最优模型外推预测2018和2019年乙肝发病率。结果 优化组合模型拟合精度最优,可选其预测我国2018和2019年乙肝发病率。结论 优化组合GM(1,1)拟合效果理想,预测精度高,可用于乙肝发病预测。

中国疾病预防控制中心法定传染病报告显示,病毒性乙型肝炎报告发病人数一直处于乙类传染病首位。且有研究表明,HBV感染不仅是干细跑癌的重要危险因素,还与B细胞恶性肿瘤之间存在相关性[1],故做好乙肝预测预警工作意义重大。近年来,灰色GM(1,1)模型已被多次应用于乙肝流行趋势的预测[2-3]。但传统模型预测精度往往不易达到要求,故本研究拟对传统GM(1,1)模型的建模维数、背景值和初始值方面改进,尽量弥补传统模型的缺陷,并采用构建的优化组合GM(1,1)模型预测我国2018-2019年乙肝发病率,为乙肝防治提供科学依据。

资料与方法

1.资料来源

本研究资料来源于中国疾病预防控制中心2007-2017年乙型肝炎发病资料及人口资料[4],详见表 1。

表1 2007-2017年全国乙型肝炎发病率(1/10万)

2.模型构建方法

(1)构建GM(1,1)的前提条件

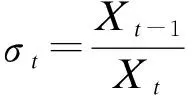
(2)传统GM(1,1)预测模型构建步骤[5]

①已知原始非负数列Xt=X1,X2,…,Xn(t=1,2,…,n),Xt一次累加数列Yt和均值数列Zt:

Yt=∑Xt

(1)

Zt=(Yt+Yt-1)/2

(2)

②Yt的白化微分方程:dYt/dt+αYt=u

(3)

其中,α为发展系数,负值反映发展趋势是增长的,正值反映发展趋势是衰减的;绝对值越大,则增长(或衰减)越快。u为灰色作用量,其大小反映因子作用的强弱,即数据变化的关系。根据最小二乘法估计:

(4)

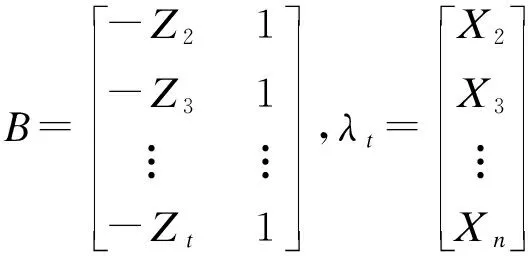
(5)

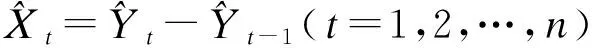
(6)

(3)最优建模维数

传统GM(1,1)模型对建模维数不作要求,但不同维数的灰色模型,其预测值也不一定相同[6]。为了提高模型的预测精度,本研究以2007-2016年全国乙肝发病率数据为例,以时间序列最后一个数据为基础分别建立4～10不同维数模型,通过比较各模型对2017年发病率的预测效果和模型的精确度,以选择最优的建模维数。

(4)背景值和初始值的改进

由传统GM(1,1)模型构建过程可见,背景值假定是由一次累加生成序列的紧邻等权生成,即权重u=0.5,樊新海[7]等学者认为没有理由证明u=0.5时模型的预测精度最高,故采用自动寻优定权的方法选择u值,即给定一接近于零的初始权u=0,计算在该权值下的模型预测精度,然后令权值有一微小的增量u=u+Δu,重复上述过程,直到u=1,即可得到不同权值下模型的预测精度,取预测精度最高时的权值作为最佳权值。另外,杨华龙[8]对模型的初始值也进行了改进,其认为数据序列中的每一个数据都带有一定的随机误差,不能将第一个或最后一个原始数值作为初始值,具体推导过程参考相关文献[8],此处只给出初始值C和时间响应函数:

(7)

(8)

其中α、u为待定系数。

原始数列Xt的拟合值:

(9)

3.模型检验

在GM(1,1)模型检验中,预测精度检验方法主要有残差检验、关联度检验、级比偏差检验和后验差检验,本研究采用残差检验和后验差检验。

(1)残差检验

(10)

MRE小于20%称模型为合格模型,模型分类等级见表2。

(2)后验差检验

后验差检验是利用后验差比值c与最小误差几率P来衡量预测模型的精度,

(11)

(12)

c=s2/s1

(13)

(14)

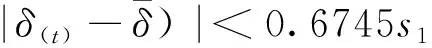
s1是衡量原始数据的离散程度,s2是衡量残差的离散程度,故c值越小表示预测模型准确度越高。最小误差几率P越大,表示残差与残差平均值的差值小于0.6745s1的数值越多,故P值越大表示预测模型越好,模型检验等级见表2。

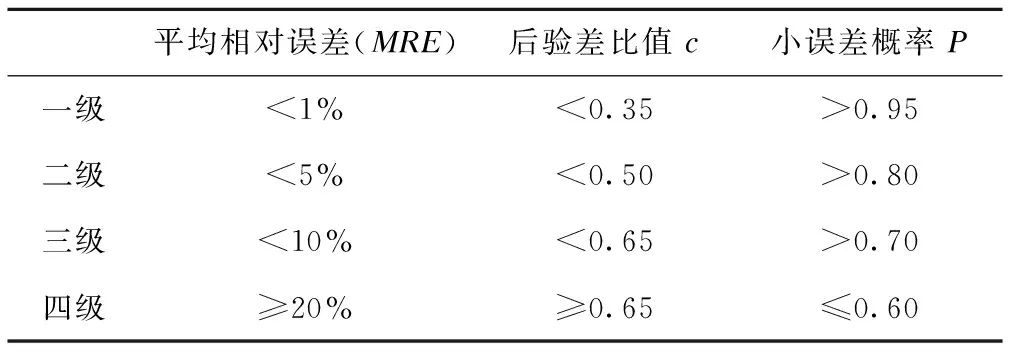
表2 模型检验等级表

结 果

1.GM(1,1)模型构建的可行性分析

2.模型的构建

(1)传统GM(1,1)模型构建

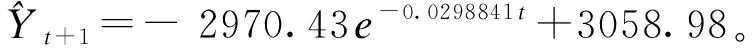
(2)最优维数模型的构建

从表3可知,并不是维数越高的模型拟合效果越好,5维模型的相对误差为5.88%,其2017年发病率预测值与实际值最为接近,且模型的MRE和c值最小,模型精度最高,故选择5维作为建模的最优维数。

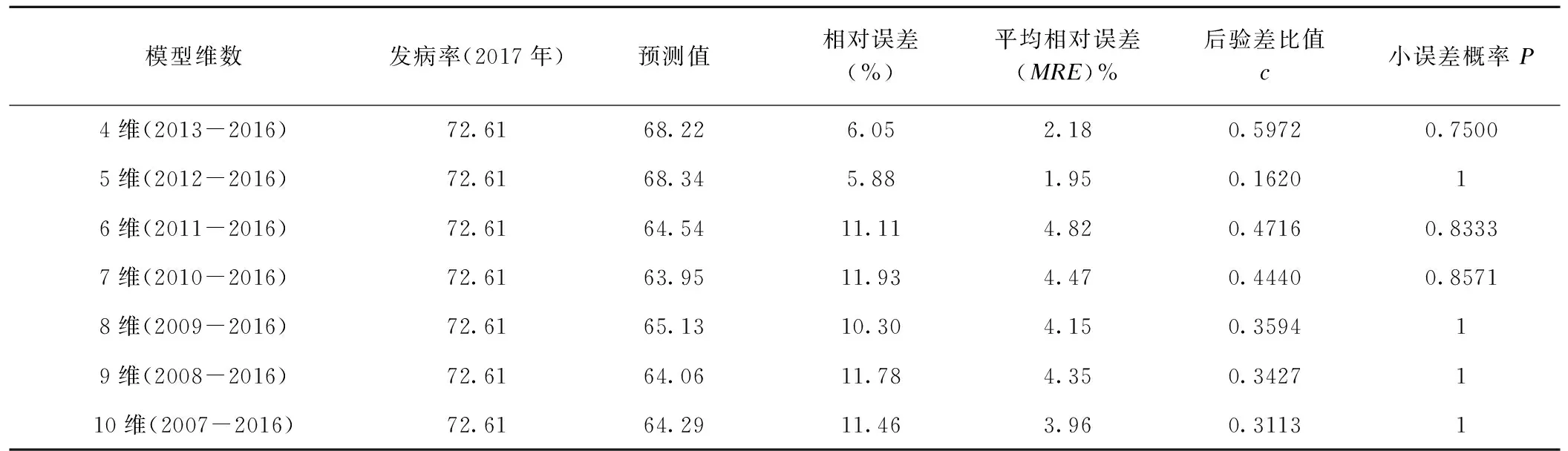
表3 不同维数GM(1,1)模型预测2017年乙肝发病率(1/10万)

(3)背景值和初始值优化模型的构建

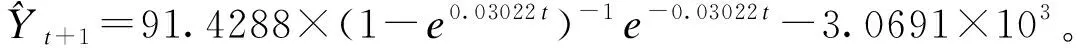
(4)优化组合GM(1,1)模型构建

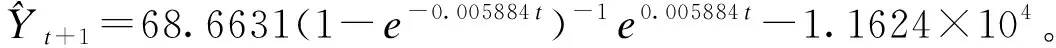
3.模型精度检验结果

分别对以上构建的4种模型进行精度检验,结果如表4所示,5维传统模型的平均相对误差(MRE)和后验差比值c均小于10维传统模型,最小误差几率P大于10维传统模型,说明维数优化可提高模型预测精度;对背景值和初始值改进后的模型平均相对误差(MRE)和后验差比值c均减小,说明此改进方法有效;将模型的维数、背景值和初始值同时改进组合得到优化组合GM(1,1),其平均相对误差(MRE)和后验差比值c最小,模型精度最高,适合外推预测2018年和2019年乙肝发病率。

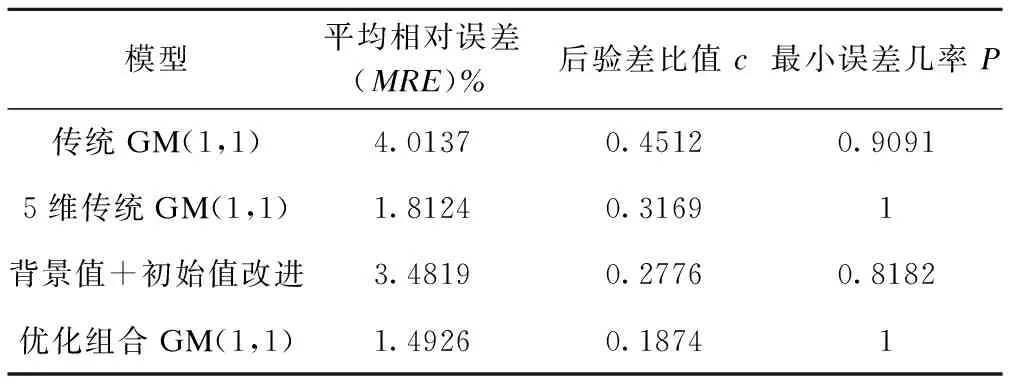
表4 不同模型精度检验比较

4.2018-2019年全国乙型肝炎发病率预测

运用以上构建的4种模型分别拟合2007-2017年的乙肝发病率并外推预测2018-2019年的发病率,结果如表5所示。由表5可知,优化组合GM(1,1)拟合2007-2017年发病率的拟合效果优于其他模型,适合外推预测2018年和2019年乙肝发病率,预测值为71.13/10万和71.55/10万。

讨 论

应用数学模型预测传染病疫情时,原始数据的质量及其是否符合建模条件是影响预测结果的关键因素。本研究使用的2007-2017年全国乙肝年发病数据来自中国疾病预防控制中心法定传染病呈报数据,计算的发病率较为可靠。当然,如果原始数列呈现线性分布特点时,可参考构建线性回归模型,合理有效的预测模型取决于实际资料分析和模型方法检验[9]。本研究经过对资料分析后,认为其满足构建灰色模型的前提条件,并且最终模型预测精度较高。通过4种模型对乙肝发病率的拟合发现,传统模型、维数优化模型、背景值和初始值优化模型的发展系数均大于0,即预测发病趋势是衰减的,但优化组合模型发展系数小于0,预测发病趋势是上升的,这可能与2017年发病率上升有关,说明优化组合模型能更好地利用新近信息,比传统模型和单一改进模型更具优势。从表5中发现,虽然优化组合模型对个别年份(2016年)发病率拟合效果不如传统模型,但其总体的预测精度远远高于传统模型。同时,考虑到GM(1,1)模型稳定性问题,根据相关理论[10],当发展系数很小时模型的稳定性较好,此优化模型,满足该条件,故可选其预测2018-2019年全国乙肝发病率。

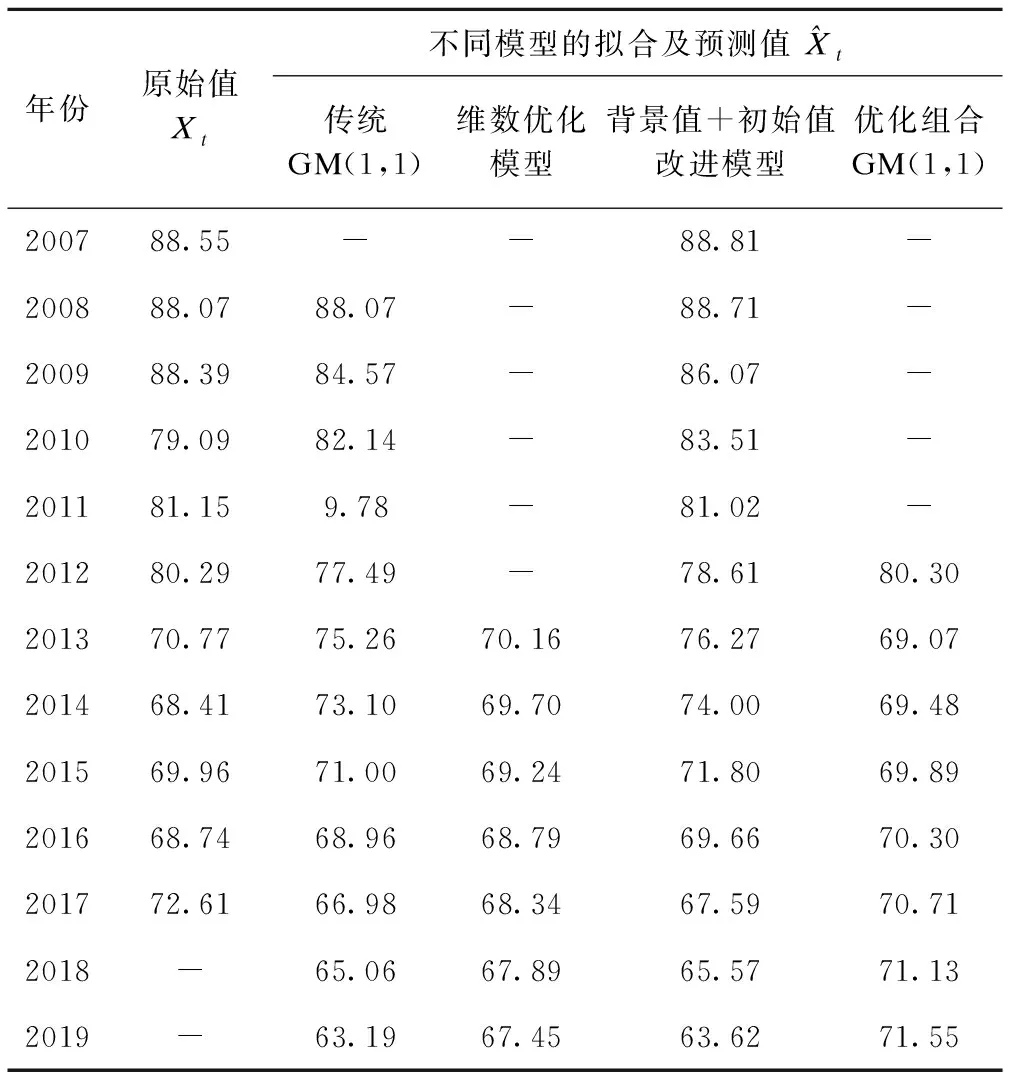
表5 不同模型对乙肝发病率(1/10万)的拟合和预测

由2007-2017年全国乙肝发病率资料可以看出,发病率总体呈下降趋势,其中2010年和2013年下降幅度较大,这可能与人群的健康预防意识提高有关,也与人群乙肝疫苗接种率增加有关,但不难发现,近几年发病率呈上下波动趋势,其中最近的年份(2017年)上升幅度较大,这也为优化组合模型预测2018-2019年发病率呈上升趋势作出合理解释,虽然预测模型的发展系数较小,但也应引起有关部门的重视,探究其发病率上升的原因,对乙肝患者做好治疗管理的同时,还要加强易感人群的防护工作,提高疫苗的接种率。通过开展一系列乙型肝炎的综合干预措施,控制乙肝的传播和流行,降低发病率,使乙肝得到有效控制。

综上所述,本研究构建的优化GM(1,1)模型可用于乙肝的发病率预测研究中。但由于本研究所用的模型具有建模数据少、无需假定数据服从某种特定的分布规律的特点[11],影响因素较多,因此该模型的预测精度有待进一步提高。同时,模型预测稳定性问题也一直是研究者关心的问题。在后期时间及经费允许的前提下,可根据已有的对稳定性理论探讨的基础[12],将模型的精度优化方法与稳定性优化方法相结合, 对其进行更深入的探索,进一步提升GM(1,1)模型的适用价值。