基于负载转矩观测器的无刷直流电机SVPWM矢量控制

田 亮，于海生，于金鹏，吴贺荣，刘旭东

（青岛大学 自动化与电气工程学院，青岛 266071）

0 引言

无刷直流电机由于其动态性能好，高效节能以及较好的机械特性，广泛应用于各种行业[1,2]。传统的PI控制策略算法简单，常用于BLDCM的调速控制，但由于PI控制策略下电机运行的精度不高，转矩脉动较大，无法满足电机高性能运行的要求。近年来，随着控制策略的发展，模糊控制、滑模控制、神经网络控制、自适应控制、矢量控制等多种非线性控制与智能控制算法逐步应用到BLDCM的控制系统中。文献[3,4]将模糊控制方法应用到了无刷直流电机控制系统，提高了电机的响应速度及其控制精度，但系统仍然存在抖振的问题。文献[5～7]在PI控制的基础上设计了神经网络控制，有效的提高了系统的响应速度和精度，却不能很好的解决系统抖振。文献[8]设计了负载转矩观测器，并将输出的转矩信号转换为电流模型，提高了系统的抗负载扰动能力。文献[9]采用空间电压矢量脉冲调制技术驱动无刷直流电机并分析了空间电压矢量的选择对电机性能的影响。文献[10,11]基于矢量控制设计了状态观测器，改善了无刷直流电机运行特性。文献[12]设计了反电势观测器和滑模控制器对转矩进行控制，提高了系统的响应速度及其抗扰动能力。文献[13,14]分别采用基于占空比的直接转矩控制（direct torque control，DTC）和无传感器直接转矩控制，降低了转矩脉动，提高了传统DTC的性能，使系统具有良好的动态性能。文献[15～17]则是设计滑模观测器，通过观测反电势改善电机的调速性能和系统的抗干扰能力。

为了克服系统转速响应慢、稳态控制精度不高、抗负载能力差等问题，本文提出了在矢量控制的基础上设计速度环积分型滑模控制器，并设计观测器估计实际的负载转矩，得到的负载转矩转换为电流信号反馈给控制器进行补偿。相比于传统PI控制方法，该控制方法能够提高BLDCM系统的抗负载扰动能力，降低转速的波动，并且能够提升系统的动态和稳态性能。

1 无刷直流电机的数学模型

为了使分析更加简便，简化系统的模型。假设无刷直流电机定子三相绕组完全对称，运行时电机磁路不饱和，忽略磁滞和涡流给电机带来的影响，同时忽略齿槽效应，则无刷直流电机的电压方程[18]为：

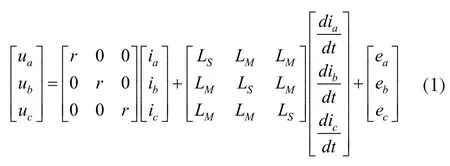
式中，ua、ub、uc表示定子各相电压，ia、ib、ic表示相电流，ea、eb、ec为三相反电势，r为绕组电阻，LS为每相绕组的自感，LM为定子两相绕组之间的互感。

当定子采用三相Y型接法时，有ia+ib+ic=0，则电压方程为：

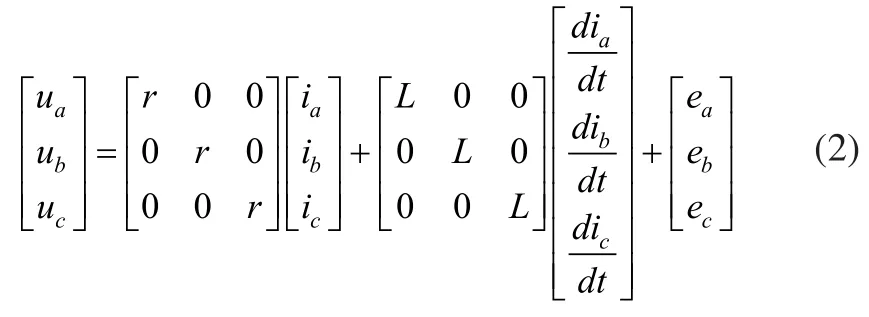
式中，L=LS-LM。

由式(2)可得在dq坐标系下BLDCM电压方程：

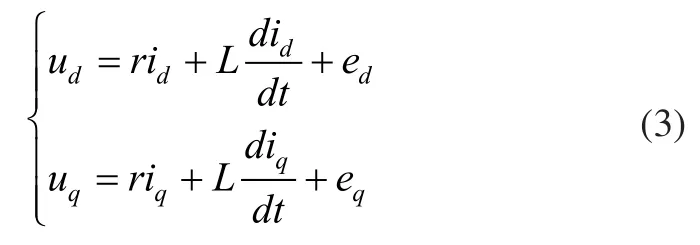
无刷直流电机电磁转矩为：

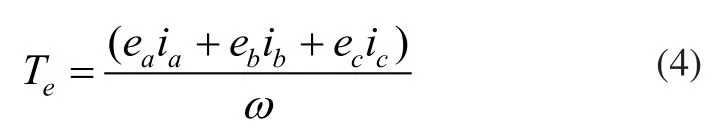
由式(4)经坐标变换得到dq坐标系转矩方程：

式中，w为转子角速度，p为极对数。

运动方程为：

式中，Te为电磁转矩；TL为负载转矩；B为阻尼系数；J为转动惯量。

2 系统控制器设计

控制系统的整体框图如图1所示。该系统将负载转矩观测器估计的负载转矩计算为电流信号，反馈给滑模控制器，完成对系统的补偿作用，达到需要的控制效果。

2.1 负载转矩观测器的设计

采用id=0控制方法时，由其数学模型表达式可以化简为[19]：

由电机运动学方程式(6)，忽略阻尼系数B有：

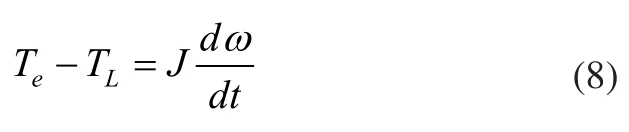
将式(7)代入式(8)中得：

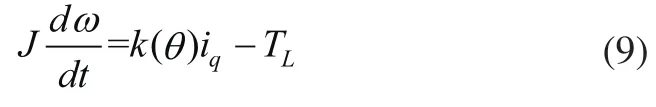
式中，k(θ)为电机的转矩系数。

根据式(9)，负载转矩已知恒定时有状态方程：

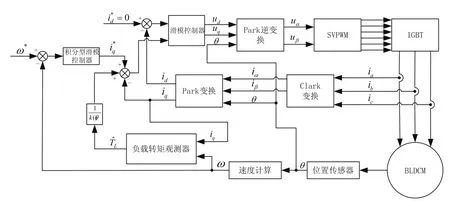
图1 无刷直流电机控制系统

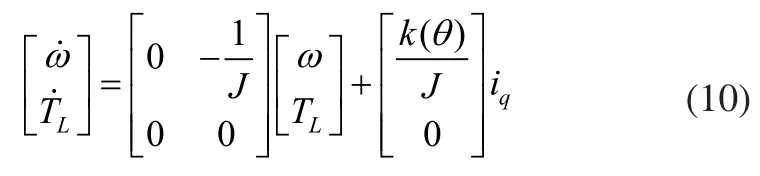
将上式写成矩阵方程的形式为：

构造负载转矩状态观测器为：

即：

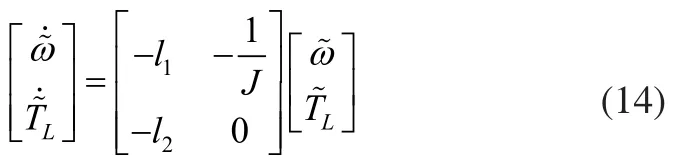
可以证明，当选择l1＞0、l2＜0时，观测器是渐近稳定的。求出由式(14)表示的系统的极点为，将两个极点s1，s2配置在同一点，即s1=s2=-m（m＞0），则有：

m的取值决定了负载转矩估计误差收敛速度，即ˆLT收敛到TL的速度。在计算完成后，将估计得到的ˆLT转换成对应的电流量，对控制器输出的电流信号进行补偿，进而削弱当负载转矩未知时给系统带来的不良影响。

2.2 转速控制器的设计

对于速度环滑模控制器，由电机期望转速ω*与实际反馈转速ω的偏差e(t)进行调节，以达到跟踪误差最小的目的。系统的状态变量为：

式中e(t)=ω*-ω。

取滑模面：

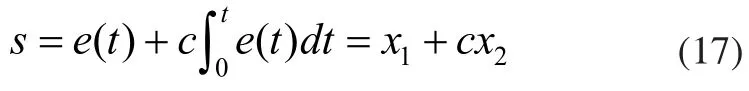
式中c为常数且c＞0。

在滑模面上，满足s=0，对s求导，根据式(8)、式(16)可以得知：

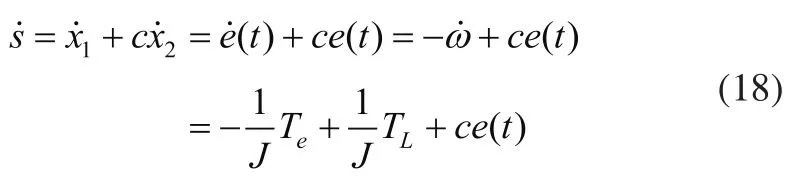
为了改善电机系统的控制效果，控制律选用指数趋近律[20]：

式中，k1、k2均为大于0的常数，sgn为符号函数。

选取Lyapunov函数：

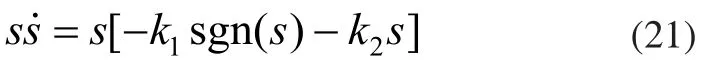
当k1＞0、k2＞0时，满足。因此，V1正定，负半定。根据Lyapunov稳定判据可以得知系统转速环渐近稳定，当且仅当时，

根据式(18)、式(19)可以得到：

根据式(7)和式(22)得出的表达式：

由于选取的控制律中存在不连续控制项k1sgn(s)，会导致系统在切换面上产生高频的抖振。为了较好的减小滑模抖振的问题，设计合理的趋近律能够有效解决该问题。在系统中利用饱和函数sat(,)sδ来取代符号函数sgn(s)，可以有效的减小系统在切换面处的抖振。饱和函数表达式：

式中，δ为边界层厚度。

结合式(23)，则控制律可以表示为：

由上述式子可以得到转速环的控制器。

2.3 d、q轴电流控制器设计

对于d、q轴电流的控制器，定义d、q轴电流误差e1(t)、e2(t)作为控制器的状态变量。

式中，i*d，i*q为给定的电流，id，iq为实际反馈的电流。

取滑模面切换函数为：

选用指数趋近律：

αn、βn为大于零的常数。

由上式经过计算可得：

由此可得dq坐标系下，电机输入电压为：

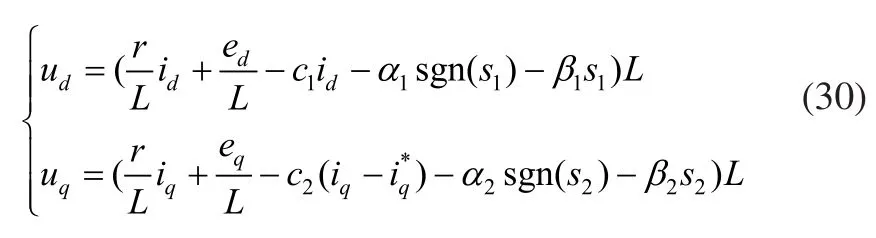
选取Lyapunov函数：

根据上式可得：

根据式(28)和式(32)有：

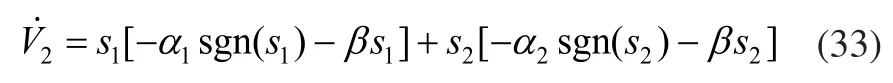
当αn＞0、βn＞0（n=1,2）时，满足≤0。因此，V2正定，2V˙负半定。根据Lyapunov稳定判据可以得知系统电流环控制器渐近稳定。当满足

3 仿真结果

为了验证该方法的控制效果，利用Matlab/Simulink搭建BLDCM系统仿真模型。设置仿真参数：

r=2.875Ω，L=0.0085H，J=0.0008kg.m2，p=2，UDC=300V。负载转矩观测器参数m=500；转速环控制器的参数为：c=3，k1=5，k2=15，δ=0.5；电流环控制器的参数为：c1=0.03，c2=0.04，α1=α2=200，β1=β2=100。

图2分别给出了未知的负载转矩曲线与观测器输出的负载转矩曲线。比较图中的两条曲线可以看出，由观测器估计得到的负载转矩可以很好的跟踪未知的负载转矩变化，从而可以满足将估计得到的转矩信号变换为电流信号反馈给系统控制器完成补偿作用。

图2 负载转矩估计曲线

将转速设定为nr=1000r/min（ω*=104.72rad/s），并接入如图2所示的未知负载转矩。图3是有、无负载转矩观测器的BLDCM在滑模控制器下的速度波形对比图，图4为负载变化时刻电机转速的放大波形图。从图中可知，在有负载转矩观测器的控制系统中，当电机系统接入未知负载时，观测器可以很好的削弱负载变化给电机转速带来的影响。

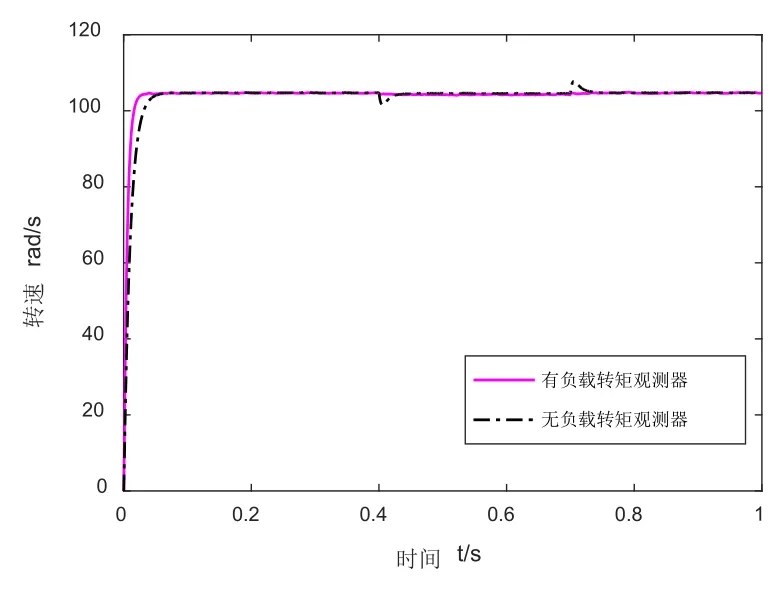
图3 有、无观测器的滑模控制对比波形

图4 存在扰动时的转速局部放大波形

将转速信号设定为nr=1000r/min（ω*=104.72rad/s），图5分别给出了传统PI控制和滑模控制下的BLDCM速度曲线，图6为图5局部放大曲线。从图中可知，基于负载转矩观测器的滑模控制比PI控制系统所需要的上升时间短、响应速度快、控制效果更好。

图5 传统PI控制与滑模控制下速度对比曲线

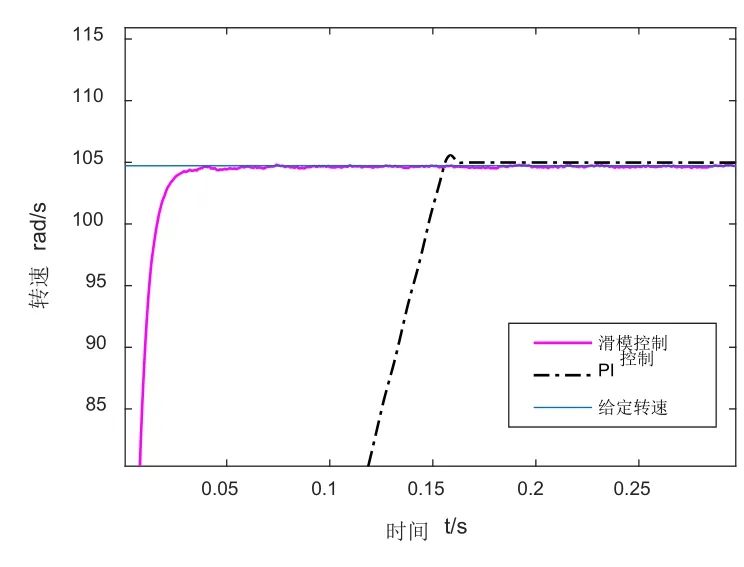
图6 图5局部放大图

4 结束语

为了提高BLDCM系统的响应速度与抗负载扰动能力，满足电机高性能运行的需求，本文基于矢量控制方法，对d、q轴电流设计了控制器；对系统的转速环设计了滑模控制器及负载转矩观测器，观测器的输出，经过计算转换为电流反馈给控制器，为了解决系统在滑模面附近的抖振，将滑模趋近律中的符号函数改为饱和函数。通过所设计的改进的控制器，能够提高系统的运行速度，降低抖振。采用设计观测器，估计的负载转矩补偿电流反馈给控制器，使得系统能够迅速响应负载的实时变化。经过仿真验证，基于负载转矩观测器的BLDCM滑模控制方案具有较快的响应速度；当接入系统的负载情况未知时，观测器能够有效的削弱负载变化给系统带来的影响，提高了系统在负载变化时的转速控制性能。