基于约束规划的整车测试排程问题研究
2018-11-02陈淮莉
陈 露,陈淮莉
(上海海事大学 物流科学与工程研究院,上海 201306)
1 研究背景及意义
汽车工业一直是经济发达国家的支柱产业之一,在国民经济中具有重要的地位。各国经济发展的经验表明,保持经济的快速增长离不开若干个高于平均增长速度的主导产业的带动。汽车工业是综合性工业,具有较强的产业波及效果和带动作用。汽车工业是附加值很高的加工工业,它的发展带动了与之相关的钢铁,机械,电子电器,橡胶等行业的发展,是创造社会财富,提高国民收入的重要来源。图1所示为历年来中国汽车销量统计,数据来源于中国产业信息网[1]。

图1 中国2005~2017汽车销量
在汽车企业,在新车型大规模生产之前,汽车制造商通常对所研发的新车辆进行数百次测试。由于是研发的新车型,配套的生产线还不存在,这些样车原型大部分是手工制造,价格一般都比较昂贵。如果测试按照合适的顺序排列,大部分原型可以进行多个测试,这样就大大地节约了制造成本。这个问题类似于并行机的调度问题,原型和测试对应着机器和作业。因此需要合理的分配测试的顺序,忽略原型的不同变型之间的成本差异,尽量减少所使用的原型数量及最大完工时间,确保尽快投入生产。
2 国内外研究现状
原型样车测试排程类似于同型机并行调度问题,这是实际制造业生产过程中一类典型的调度问题。早期学者Garey和Johnson证明了在机器数量模糊的情况下,以最小化加工时间为目标的并行机调度属于NP-Hard问题[2]。Pinedo在其文章中指出并行机调度已经引起了众多学者的广泛关注与研究,并在许多行业有了成熟的发展与应用[3]。汪恭书等[4]研究了目标函数以最小化总加权完成时间,工件具有最迟开始处理时间的并行机实时调度问题,建立了混合整数规划模型并融合了拉格朗日(LR)和列生成(CG)的混合算法。Scheffermann等[5]针对考虑投放时间、截止时间以及其他条件的调度问题,提出一种启发式搜索策略,但利用概率统计的方法调节影响原型样车数目的参数仍有一定的困难。Sadykov和Wolsey[6]针对考虑投放时间和截止时间的并行机任务分配问题,提出了整数规划和约束传播求解方法。采用区间情景来刻画加工时间,并采用最小最大遗憾原则,许晓晴等[7]研究了不确定加工时间下同型并行机的鲁棒排程。
目前,计算机仿真技术已经应用于执行各种测试,例如在驾驶室进行传热模拟、风洞试验、碰撞模拟等。然而,Kohlhoff[8]坚持使用真实的原型样车进行测试,毕竟计算机仿真与模拟的准确性和可靠性有限。不考虑组件要求和样车变体选择过程,Schwindt[9]应用混合整数线性规划求解了简化的调度问题。
除了这些以前的研究,有几个与汽车制造商的汽车测试相关的项目。他们的问题特点略有不同,并使用各种不同方法解决。然而,他们都有相同的目标,就是降低测试过程的成本。对于福特汽车公司,Lockledge等[10]应用多级数学规划模型优化原型船队。第一步,他们确定所有测试的组件要求所需的变种数量。第二个模型确定每个变量的最低数量的汽车,使得所有的测试可以在到期日期之前执行。Bartels和Zimmermann[11]考虑了组件的要求和时间的限制,只是一些额外的约束略有不同。他们考虑部分有序的破坏性测试,而不是在相同或不同的原型执行测试。例如,驾驶测试,可能会损坏机箱,使这个原型不再适合进行声学测试。因此,此驱动测试在声学测试之后执行,或者它们被分配在不同的原型上。他们提出了一个混合整数线性规划配方可用于解决小规模的问题。为了处理较大的情况下,他们提出了一种启发式方法的基础上的优先级规则。Zakarian[12]为通用汽车卡车集团开发了一个分析模型和决策支持工具,以评估性能的产品验证和测试计划。他模拟与测试时间和产品故障相关的不确定性,以确定验证计划中使用的车辆数量和完成测试的百分比之间的权衡。
3 模型建立
3.1 问题描述
大部分汽车制造商都有专门生产汽车原型的工厂,由于工厂空间容量有限,汽车原型依次按照要求制造出来,这就会产生每个原型的可用时间。在原型制造之后,原型需要初始设置过程,其持续时间取决于原型的所选变体以及该原型上计划的测试序列。例如,在执行腐蚀测试时原型必须涂漆,而在执行碰撞测试时就不需要涂漆。因此只有建立好指定的原型才能进行测试,而且有效的排程必须满足所有的时间约束。图2为原型样车(prototype)测试示意图,中间的横线代表用于测试的m辆原型样车,这些原型样车用来完成右边所示的n项测试,左边所示为准备完好的l个样车变体。一辆样车的各个组成部件有多种类型,不同类型的组成部件之间会有大量的组合方式,这些组合方式是为了测试不同组件之间的协调性和相容性,满足每项性能测试的特殊要求。
本文使用约束规划(Constraint Programming)来求解测试排程问题。原型样车的数量是离散的,而完工时间是连续的。因此本文中采用经典的参数化方法,即在所有约束条件下确定了原型的数量并最小化了完工时间。最初假设大量的原型,使得完工时间只取决于时间的限制。然后反复减少原型的数量,然后再解决问题,这就产生了原型数量和完工时间之间的关系。
约束规划是制定和解决一个优化问题的另一种确定性方法。它最初是为计算机科学应用,经过几十年的发展,约束规划已经在规划、调度、生物信息学、车辆路径、配置等领域得到了广泛的应用。要应用约束规划,首先将需要描述的问题制定作为一组决策变量和约束。每个变量有自己的有限集的可能值(域),而约束限制的值,变量可以同时采取。约束规划的解决方案是一个值分配给每一个变量,使所有的约束满足。接下来,可以指定一个搜索方案来描述求解器如何从可能的分配中进行枚举,到实现一个解决方案。当搜索过程中出现矛盾时,约束规划有一个叫做回溯的功能来继续尝试其他可能的决定。

图2 原型样车测试流程图
约束规划在表达约束方面优于混合整数规划(MILP),因为它不局限于线性不等式。例如,它支持逻辑表达式,像if…else,而不是使用许多复杂的线性不等式来表示机器的资格约束,这样复杂的调度问题就可以用逻辑表达式自然地表示出来。
3.2 参数设置
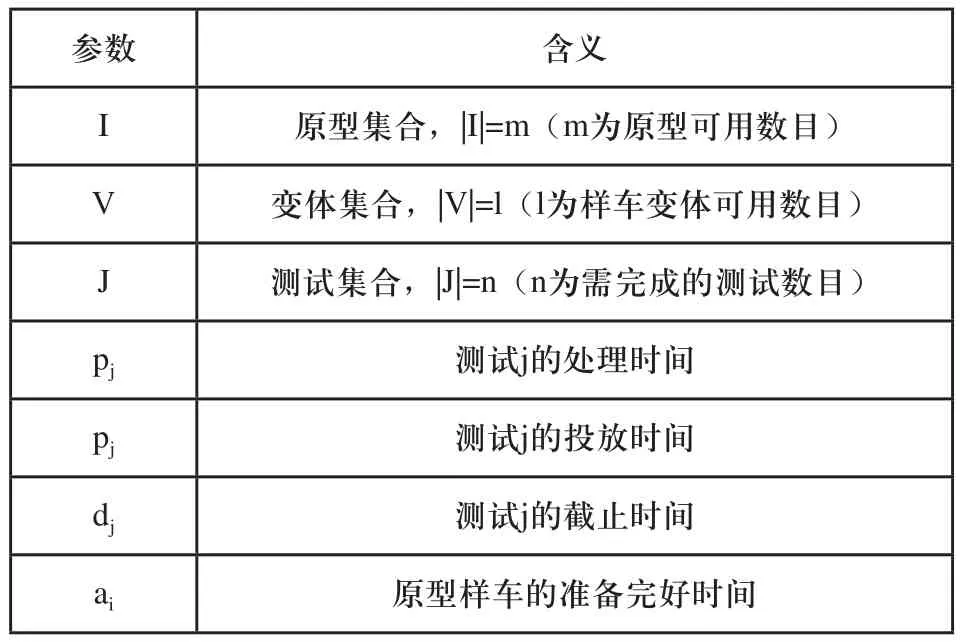
表1 模型参数
VMj⊆V 表示可以进行测试j∈J的 原型变体集合。由于测试时不间断的,测试j的完成时间cj必须满足, 最大完成时间cmax= maxj∈J{cj}。此外,每个原型i⊆I有 一个可用的时间ai,原型建立时间Svi,由变体vi决定;在原型制造时,一些组件无法及时到达并进行组装,原型交货时间为yv,变体v的建立被延迟,因此测试时间必须在时间max{ai+svi,yvi}之后才能开始进行测试。
3.3 考虑两个测试之间的关系,j,k ∈J
j<k表示测试j必须在测试k之前完成;
j~k表示测试j和测试k必须在同一个原型上进行;
j≠k表示测试j和测试k不能在同一个原型上进行;
JLast⊆J表示在同一原型上的最后一项测试集合。
在用约束规划解决测试排程问题时,参照资源分配问题引入向量[t,p,c,C],t=[t1,…,tn]表示测试起始时间向量,p=[p1,…,pn]表示每项测试处理时间向量,c=[c1,…,cn]表示工作消耗率向量,C是机器容量(machine capacity)。是时间t在进行中的任务集合,如果在有效的时间中所有时间t都满足,那么约束就是被满足了。因此,所有测试工作的总消耗率不会超过机器容量C。设每个原型容量C=1,每个测试需要单个的原型,。
另外还需定义一些变量,每个测试j的起始时间tj必须在区间内,遵从投放日期和到期日的限制。表示测试j分配给原型i。表示原型i的变体。
3.5 约束条件
约束(1)确保完工时间不小于任何测试的完成时间。约束(2)和约束(3)规定测试必须在各自的投放和到期日期之间执行。约束(4)是资源约束,(tj|xi=i)表示分配到原型i上的测试开始时间的数组。约束限制了两项测试在一个机器上同时执行。约束(5)表示防止将测试分配给不具备测试所需条件的变体的原型。约束(6)和约束(7)确保机器i上的测试在原型的可用性之前开始。原型设置建立时间svi,组件可用时间yvi取决于变量vi的值,在问题得到优化之前这个值是未知的。CP方法的另一个好处是变量可以索引参数数组。约束(8)表示优先约束。约束(9)表示测试j和k在同一个原型上执行。约束(10)表示测试j和k必须在不同原型上执行。约束(11)表示测试∀j∈JLast是分派到该原型上的最后一项测试。
4 算例分析与结论
为验证本文解决策略的实用性及有效性,使用OPL Studio12.6实现了本文的算法。从现实的汽车制造厂商选取一组具有代表性的数据,测试个数从几十到几百个。表2给出了相关实例的计算结果,包括所需要的原型数量,计算时间,特殊约束等。对于测试数目比较大的数据,特殊约束对结果会产生比较大的影响。
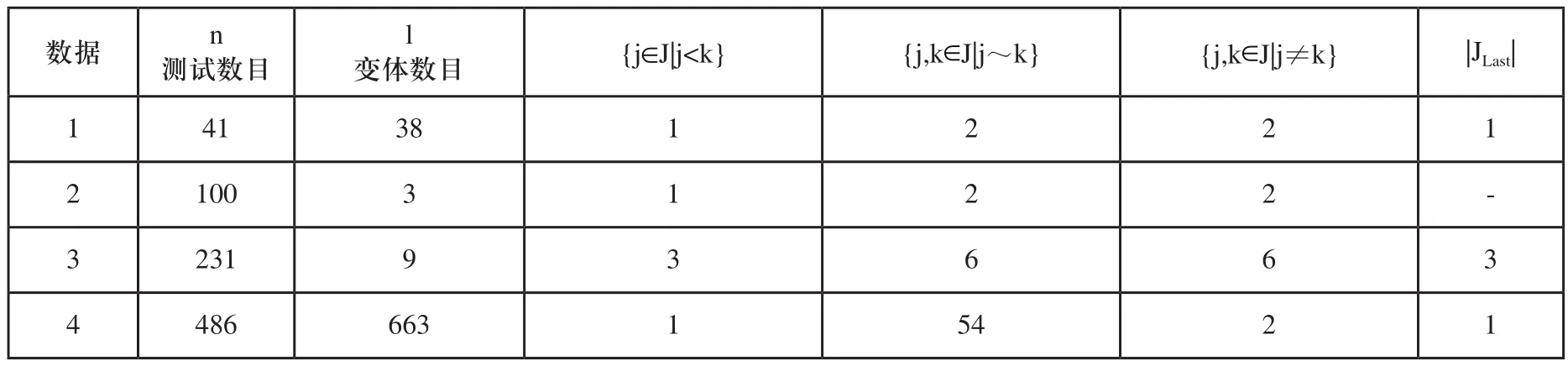
表2 给定数据集的具体信息
本文是采用ILOG CPLEX Optimization Studio来求解的,除了标准的功能之外,OPL还有具体的调度模块,包括解决调度问题的几种功能。此外,它还具有良好的约束传播技术和高效的搜索方法。表2中列出的变量和约束条件与前文中建立的模型相对应,给出了他们在计算过程中给出问题大小及其变化的规律,研究了给定原型数量与最大完工时间之间的关系。
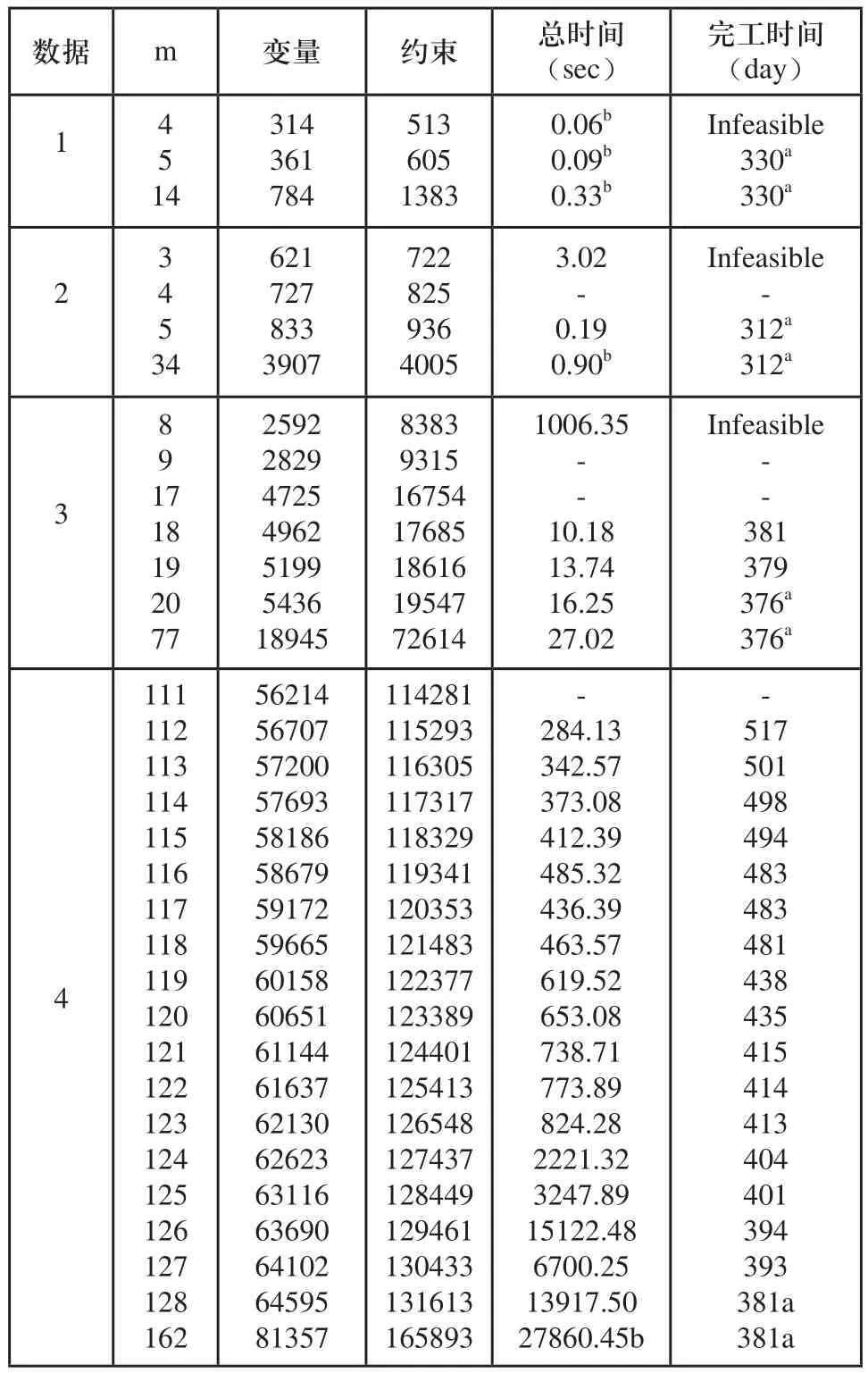
表3 给定原型数量的最小化完工时间
表3显示了计算结果。 对于每个数据集和给定数量的原型,使得完工时间最小化。 最初可以将m设置为一个很大的值,这意味着需要尝试构建尽可能多的原型,以适应所有的测试。在某些情况下,例如如果在很早的到期日期内进行了很多测试,原型可能太晚了,这个过程不会产生一个可行的解决方案。但是,产生这个冲突的原因可能来自时间约束,而不是有限的原型数量。
在获得结果之后,逐步减少原型的数量,看看它是如何影响到完工时间的。重复此过程,直至找到找不到可行的解决方案,或者计算无法在给定时限内终止。本文中规定数据1~3的时间限制为1小时,数据4的时间限制为6小时。例如在数据1中,从m=14开始,获得330天的完工时间。如果只限制5个原型,仍然可以得到相同的最佳完工时间。但是,如果设定m=4,那么问题变得不可行,因为它没有足够的原型来执行所有约束的所有测试。
如果有足够的时间,求解器要么可以为这个原型获得最优解,要么证明这个问题是不可行的。但是,当问题规模变大时,所需的计算时间会迅速增长。由于实践中计算时间的限制,解算器可能无法证明问题的不可行性。即使找到了可行的解决方案,只要搜索树中还有未探索的节点,这样就不能确定它的最优性。
结果表明,对于所有数据集,当给定原型的数量足够大时,可以实现最优解。如果可用原型的数量减少,则找到任何可行的解决方案或证明最优性会变得越来越困难,尽管变量和约束的数量减少了。然而,如果原型的数量减少得足够多,那么求解器可以再次在限制时间内证明不可行性,因为搜索空间已经大大缩小。例如,对数据3的计算表明,当m=20时,可以得到最优解。对于m=18或者m=19,在1小时的计算时间之后发现了可行解,但是,在9≤m≤17原型的范围内有一个未知的差距,无法确定这个问题是否可以解决。
此外,应该注意的是,步骤m中的完工时间的最优值可以被认为是下一步m′=m-1中的完工时间的下限。这可以在约束更紧的情况下减小搜索空间。然而,这个想法在这里不能有效地实施,因为在发现最佳解决方案的每种情况下,完成时间实际上是由具有很长处理时间的测试的最早完成时间(rj+pj)确定的。通常在约束传播期间,完工时间的下限已经被限制为大于或等于所有工作的最早完成时间。
5 结束语
研究了汽车原型的测试排程,并以实际数据进行算例分析,通过算例的分析证明模型是有效的,可以在测试关系约束和和时间约束的条件下,通过改变不同给定原型的数量,研究其与完工时间之间的关系。但本文建立的模型未涉及到测试过程中测试处理时间不确定的情况,有待进一步研究。
