一种基于多距离约束的高精度组网方法

赵子越，甘晓川，马骊群

（中国航空工业集团公司北京长城计量测试技术研究所，北京 100095）

0 引言

在航空航天等大型装配制造领域，数字化测量技术逐步融入到自动化生产线中，并成为控制产品质量的重要手段[1]。其中，制造业现场条件下测量任务的多样性、测量精度的高需求及测量范围的需求，使得传统的大尺寸单一参数的测量或者是由单一站位组网的测量网络难以满足测量精度和范围的要求，需要采用一种多站位或多移动站位的组网方法[2,3]。在满足测量范围和测量效率的前提下，尽可能的提高测量精度，是满足现场复杂测量任务需求的手段[4]。因此，高精度的组网方法成为近年来大尺寸测量的热点问题，并在大型飞机制造、数字化造船、智能装配等领域获得广泛关注[5,6]。目前，大尺寸距离测量可以达到较高精度，目前AT901-B激光跟踪仪干涉测距精度可达到±0.5um/m[7]，采用多个距离观测量进行优化解算是研究高精度组网问题的一个思路。在国外，德国的Etalom公司开发了LaserTracer-NG激光跟踪干涉测量系统，采用4-5站位激光干涉仪组网测量，可以达到9m测量范围内0.2um+0.3um/m的精度，是目前文献可参考的最高精度，目前该技术受国外垄断[8]。在国内，解放军工程大学的范百兴教授研究了多站位激光跟踪仪的组网方法，在现场获得了应用[9]；天津大学的邾继贵教授团队研究了空间测量定位系统的组网方法，达到了亚毫米的精度[10,11]。

测量精度是衡量组网性能的重要指标，是能否顺利应用到制造业中的关键，高精度的组网方法是作为关键技术得以重点研究[12]。本文研究了一种基于多距离约束的高精度组网算法，采用多个距离测量站位对空间中多个测量点进行距离测量，利用多个高精度距离值的约束进行优化求解完成高精度组网。首先，介绍了组网的基本原理和数学模型，在此基础上利用多个距离约束构建约束方程，并根据距离观测量的不确定度对每个方程进行加权处理，采用Levenberg-Marquardt算法进行最优化求解，为保证迭代过程设计了合理的迭代初值求解方法。最终通过实验验证了组网方法的精度，并在工业现场中得到广泛应用。

1 数学模型

1.1 算法基本原理

基于多距离约束的组网方法的实现途径是，空间内有m个可进行距离单一参量测量的测量站，具备n个空间测量点，观测量为每个测量点距离每个测站的距离。记第i（i=1，2，…，m）个测量站观测到的第j（j=1，2，…，n）个测量点的距离观测量为Lij。原理示意图如图1所示。

图1 基于多距离约束的组网方法原理示意图

因此，可以列以下观测方程：

其误差方程可以表示为：

式中，(xj，yj，zj)表示第j个测量点的全局坐标系下坐标，(txi，tyi，tzj)表示第i的测量站位的位置，均属于未知参数。若m个测量站均可对n个测量点进行测量完成组网，考虑到未知参数不包括测量站位的旋转参数何尺度因子，整个网络中的未知参数个数k可以表示为：

每测量一个距离值均可列写一个观测返程，因此组网方程组中方程的个数k0可表示为：

若方程组可解，要求方程个数大于未知参数个数，可得：

进一步可得，测量站位数m和测量点位数n满足以下条件：

式中，m，n均未正整数，因此测量站位数和测量点位数均最小为4个，m和n最小的取值对应关系如表1所示。

表1 测量站位数m和测量点位数n的对应关系

从表1中可以看出，若使方程可解，测量站位数最少为4个，同时定向点数最少为12个，随着测量战术增加，所需的测量点数可以减少，但是无论测量站位数如何增加，测量点数最少不能少于4个。为保证组网精度，应尽可能多的布置测量点位。

考虑到距离观测量的不确定度随着距离增加而增加，例如激光跟踪仪AT901-B的干涉测距精度可达±0.5um/m，因此可以根据距离的观测量值给每个方程进行加权处理，从而提高约束效率。方程(2)乘上权值可以表达为：

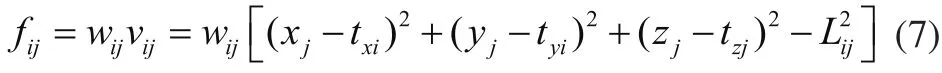
权值wij的大小与观测量Lij的不确定度uij有关，可以表示为：

因此，观测量Lij的不确定度uij越小，约束方程fij的约束就越强，权值wij就越大；反之，观测量Lij的不确定度uij越大，约束方程fij的约束就越弱，权值wij就越小。

1.2 最优化求解方法

方程(7)为二次方程，一般来讲求解这样的方程组往往比较困难。所以在解的存在性尚未确定的情况下来求解，常常将其转化为二次泛函形式。记由方程(7)组成的方程组f=0，取函数：

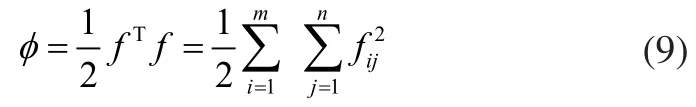
函数φ的极小点即为方程组的最小二乘解，可采用多种非线性优化方法求解[13]。其中Levenberg-Marquardt法是介于牛顿法与梯度下降法之间的一种非线性优化方法，它是利用梯度求最大（最小）值的算法，属于“爬山”法的一种，该算法鲁棒性好，对于过参数化问题不敏感，能有效处理冗余参数问题，使代价函数陷入局部极小值的机会大大减小[14,15]。因此，本文采用Levenberg-Marquardt法求解多距离约束组网问题。

1.3 迭代初值求解

Levenberg-Marquardt算法是一种迭代优化算法，在优化前需要给出合理的迭代初值，且为避免优化陷入局部最优值，要求迭代初值尽量准确，应充分接近全局极值点[16]。因而，迭代初值求解问题是多距离约束组网算法求解的关键问题。

基于多距离约束的测量系统坐标系的建立类似于GPS的定位过程，可以将4台或多于4台距离测量站位看作是相应数目的卫星，只是测距的方式是激光干涉测距。因此，基于多距离约束的测量系统系统的坐标解算可以借鉴GPS定位的方法[17,18]。本文为阐述方法，以4站为例进行说明。

基于多距离约束的组网问题中距离观测方程可写为：

其中：ρi为待求取的点到第i站位的距离，为已知量，i=1，2，3，4；

xi，yi，zi分别为第i站位的位置坐标，为已知量，i=1，2，3，4；

xu，yu，zu为待求取的坐标，为未知量。

式(10)是个非线性方程，其经典解法是利用微分将非线性的伪距方程线性化。求解过程涉及大量的偏导和迭代计算。而Bancroft算法的核心思想是用巧妙的变量替换，将多维非线性方程组转化为一元二次方程。这样就不需要再做迭代和求偏导的运算了。下面给出详细说明利用Bancroft算法来求解距离方程(11)。

首先做如下代换：

代入式(11)，得：

再令：

代入式(13)，得：

后式减去前式，得：

用矩阵形式表示为：

记：

将a，b，c用d来表示，则有：

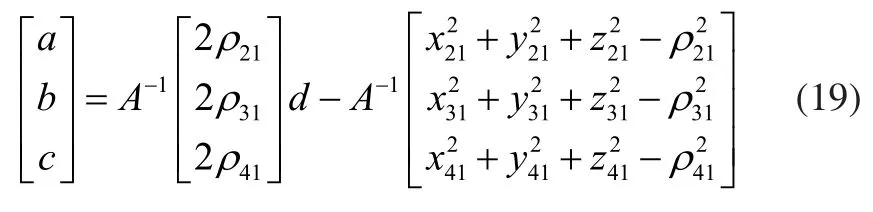
令：

可以得到：

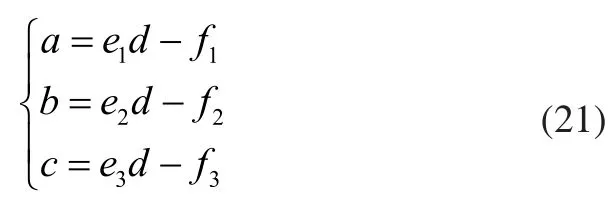
将上式代入方程a2+b2+c2=d2，得到：

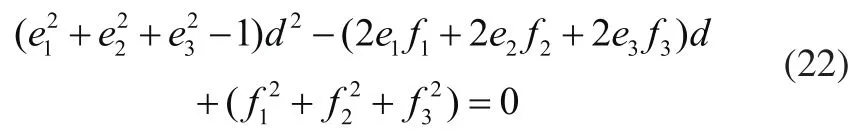
令：

式(22)的解为：

于是，可得到：

共得到两组解，也就是未知点的坐标，其中一组是不符合要求的，需要舍去。

2 实验验证

为验证组网算法的正确性和精度，在实验室条件下设计了验证实验。实验中距离传感单元采用激光跟踪仪来代替，型号为AT901-B，为节约成本，采用激光跟踪仪多次移动站位完成测量，精度验证结果采用一维标准器和正四面体标准器的比对结果给出。实验现场如图2所示。

图2 实验现场图

2.1 一维标准器比对实验

一维标准器是一种现场常用的验证标准器，采用线膨胀系数较小的殷钢材料制成，两端具备可测量点位，且两点间的距离精确已知；并附带调姿装置，能有效保证现场条件下姿态和位置可调。在10m×10m×2m的被测空间内，布置12组一维标准器，且一维标准器的标准长度已知。为达到综合验证的目的，一维标准器的方向多样化（水平、竖直方向均布置）。采用5个站位移动激光跟踪仪，测量每个站位到一维标准器两端测量点的距离，以此为观测量通过上文的组网方法完成组网求解，可得到24个点位坐标。将对应点位求距离，并与一维标准器的标准值做差值，以此误差作为组网评定的标准。实验数据如图3所示。

图3 一维标准器的比对误差

由图可知，横轴代表一维标准器的个数，纵轴代表比对误差，单位为um。经过对比可知，最大误差为2.9um，最小误差为-2.8um，全部误差均在±3um以内。可得，基于多距离约束的组网方法距离误差优于±3um。

2.2 正四面体标准器比对实验

表2 正四面体标准器的坐标比对结果

为进一步验证基于多距离约束的组网方法的坐标测量精度，采用正四面体标准器进行比对。正四面体标准器由4个坐标已知的目标点组成，所有目标点由殷钢杆连接，因此4个目标点的坐标具备极高的稳定性，可采用坐标差值的对比来评价组网精度的优劣。同样采用激光跟踪仪移动5次站位，按照上文中阐述的方法完成组网，组网完成后可得到正四面体标准器的4个目标点在测量坐标系下的坐标，将其转换到正四面体坐标系下进行求差比对，得到结果如表2所示。

在表2中，dX、dY、dZ分别代表X轴、Y轴、Z轴的偏差值，dMag代表坐标偏离值，可由下式计算：

由结果可得，单一坐标轴的偏差X和Y轴均在±2um以内，Z轴在±1um以内，dMag值在6um以内。

另外，以上两组验证实验的结果多次在实验室条件下完成验证，具备一定的稳定性。

3 结论

本文介绍了一种基于多距离约束的高精度组网方法，详细阐述了组网方法的数学模型，在合理构建约束方程的前提下，采用了Levenberg-Marquardt最优化方法完成求解，同时给出了精确的迭代初值获取方法，最后在实验室条件上进行了实验验证，实验结果表明，与一维标准器比对的距离测量精度优于±3um，与正四面体标准器比对的坐标测量精度优于6um，满足制造业中数字化测量的要求。另外，测量站位的布局也是影响测量精度的重要因素，未来可以开展相关技术研究，以适应制造业的快速发展。