基于极限学习机的有限时间自适应姿态控制*

殷春武 佟 威 何 波

西安建筑科技大学信息与控制工程学院，西安 710055

航天器在执行空间任务时，必须保证其姿态稳定，但受环境和航天器自身运动的影响，航天器的姿态常会发生偏移，姿态跟踪控制器主要用于航天器的姿态稳定控制。航天器一方面受导航带宽及角速度陀螺量程的限制，存在角速度有界约束，另一方面，航天器附件的形状改变(如机械臂伸展、太阳帆展开)会带动其质心偏移，导致姿态控制系统中的参数发生未知摄动。因此，研究存在角速度有界约束、参数摄动及外部干扰等约束下的姿态跟踪控制，具有重要的实际工程应用价值。

学者在不同的假设条件下，采用非线性控制理论和方法，设计了不同的航天器姿态跟踪控制器[1-5]，其中滑模控制因其对参数摄动的强鲁棒性，被广泛应用于干扰上界已知条件下的姿态跟踪控制器设计[1-2]。实际工程应用中，转动惯量摄动和外部干扰的上界均不可能预先知道，因此，航天器动力学方程的干扰上界已知的假设并不成立。为解决航天器动力学方程的干扰上界未知的问题，学者利用自适应技术[3-4]或智能逼近技术[5-6]对上界未知干扰进行估计或补偿，设计自适应姿态跟踪控制器，解决了航天器姿态控制系统中存在未知参数摄动的问题。但这些自适应姿态控制器在设计过程中，并没有考虑角速度有界的约束问题，且控制器结构较为复杂，无形中会增加航天器的故障率。因此，考虑角速度有界约束和简化控制器结构，提升姿态控制器的鲁棒性是本文的主要研究目的。

航天器角速度有界约束是当前学者关注的热点问题[7-9]。为满足角速度有界约束，学者主要采用障碍李雅普诺夫函数设计姿态控制器，但仿真结果显示，该控制器下的航天器角速度会不断振荡，影响航天器姿态收敛的动态品质。为解决角速度收敛震荡的问题，本文将通过规划角速度变化轨迹，使角速度平滑收敛到0，提升姿态收敛的动态品质。

反演控制具有设计便利的优势，本文对反演控制进行简化，根据航天器姿态控制系统的特点，给出一种双环跟踪控制策略。为提升控制器的鲁棒性，将极限学习机逼近技术和滑模控制技术用于双环姿态跟踪控制器的设计中。在双环跟踪控制过程中，最关键的问题是要求实际角速度在有限时间内精确跟踪上预设虚拟角速度，因此将有限时间控制用于本文姿态跟踪控制器的设计。终端滑模控制因具有较好的鲁棒性和抗干扰性，被广泛应用于非线性系统的有限时间控制器设计中[10]。本文将构建一个基于角速度跟踪误差的非奇异终端滑模面，使角速度跟踪误差在有限时间内收敛到0。设计极限学习机逼近未知摄动部分，构造自适应姿态控制器，最终实现整个闭环系统的渐近稳定性。该控制策略解决了航天器角速度有界的约束问题，简化了控制器结构，使航天器对参数摄动和外部干扰具有较强的鲁棒性，保证航天器的姿态收敛轨迹具有较优的动态品质。

1 跟踪控制问题描述

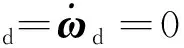
基于单位四元数{q0,q}={q0,q1,q2,q3}的航天器姿态运动学方程为

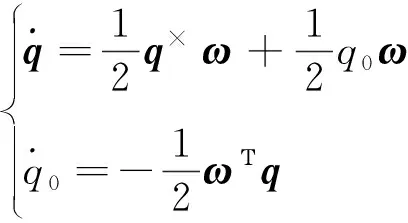
(1)

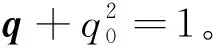
考虑外部干扰的姿态动力学方程为：

(2)

式中,J=JΤ∈R3×3为转动惯量阵，设J0为名义转动惯量，ΔJ为转动惯量摄动量，则J=J0+ΔJ。d∈R3为干扰力矩；u∈R3为控制力矩；ω×为ω=[ω1,ω2,ω3]Τ的反对称矩阵

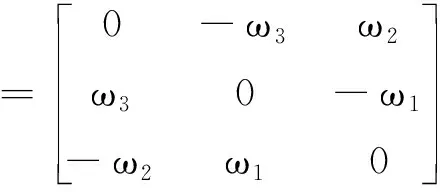
(3)

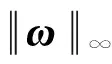
q(t)→0,ω(t)→0

(4)

在设计控制器前，先给出如下引理。

引理1[12]：如果存在正定Lyapunov函数及参数λ1>0,λ2>0和0<α<1满足：

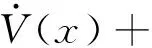
(5)

则系统状态能够在有限时间内到达原点，且到达时间为：

(6)

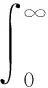
2 极限学习机建模原理

机器学习方法能有效提升拟合精度，结合实际的生物习性等，学者提出了一系列的机器学习方法，早期的机器学习方法有人工神经网络(BP),支持向量机(SVM),但是实际工程应用中发现，BP神经网络计算复杂,SVM拟合速度很慢,而基于神经网络提出的极限学习机(Extreme Learning Machine ，ELM)通过随机产生隐层结点参数,再利用计算的外权决定输出，大大简化了传统神经网络复杂的迭代过程，在保证高精度拟合的基础上降低了外权的运算量[14]。下面给出极限学习机的建模原理。

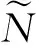
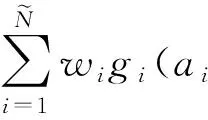
(7)

其中，ai=[ai1,ai2,…，ain]Τ∈Rn是第i个隐含层结点连接所有n个输入结点的连接权重向量；wi=[wi1,wi2,…，wim]Τ∈Rm是第i个隐含结点连接所有m个输出结点的连接权重向量，其中ai·xj表示向量ai和向量xj的内积。

经过对N个样本的不断学习则有如下线性矩阵方程成立：

HW=Y

(8)

其中，

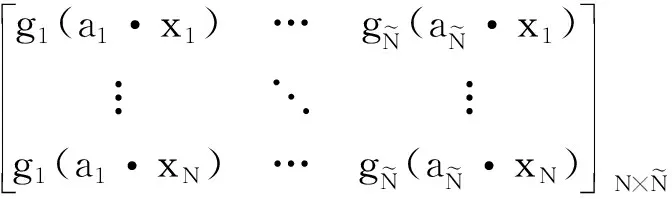
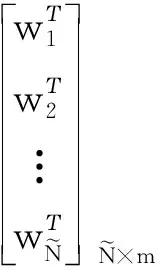
H一般称为神经网络隐含层输出矩阵，其中H的第i个列是第i个关于输入x1,x2，…，xN的隐含层结点输出。

3 双环自适应跟踪控制器设计

双环姿态跟踪控制器的结构图如图1。其主要思想是将航天器姿态动力学系统(1)和(2)分解为2个独立的子系统—内环和外环。将子系统(1)中的ω看作输入，设计虚拟控制器ωv，使子系统(1)跟踪上期望姿态qd。再将ωv看作子系统(2)的期望轨迹，设计控制器u，使子系统(2)在有限时间内精确跟踪上ωv，形成有限时间双环跟踪控制策略。

3.1 外环有界虚拟控制器设计

为满足航天器角速度有界的物理限制，提升姿态收敛速度，对子系统(1)设计虚拟角速度:

ωv=-ωTtanh(k1q)

(9)

式中，ωT>0为ωv的最大允许值；tanh(·)为双曲正切函数，常数k1>0。

设Lyapunov函数V1(q)=(q0-1)2+qΤq，则

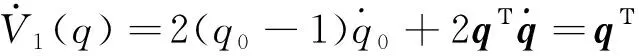
(10)

将式(1)中的ω用ωv代替，有

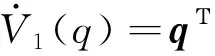
(11)

根据Lyapuno稳定性理论容易推出，当t→∞时，q0→1,q→0。

下面设计控制器u使ω有限时间内跟踪上ωv。定义实际角速度ω与虚拟角速度ωv的跟踪误差 ：

e=ω-ωv

(12)

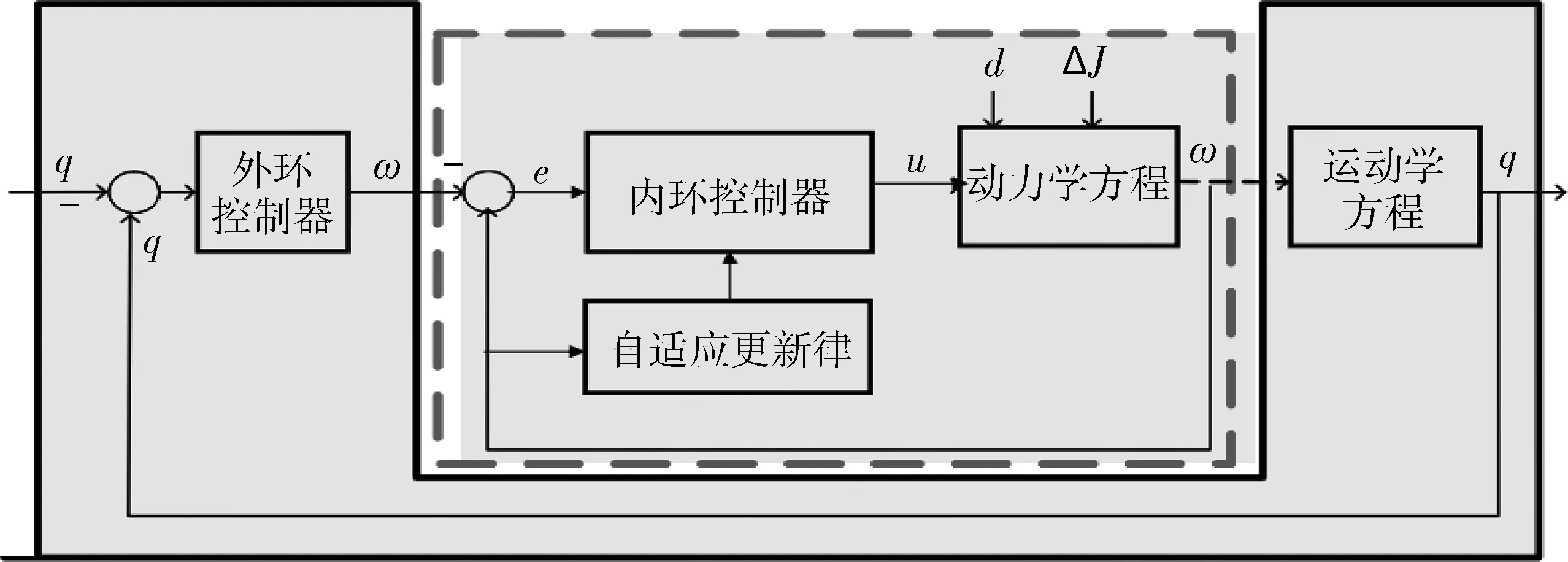
图1 自适应双环跟踪控制结构图

3.2 非奇异终端滑模面

定义非奇异终端滑模面为：

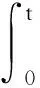
(13)

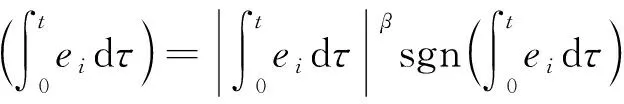
定理1： 考虑动力学系统(2)，则由式(12)和(13)确定的非奇异终端滑模面满足σ=0时，系统能够在有限时间内收敛于{e≡0}。

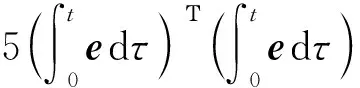
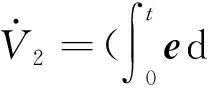
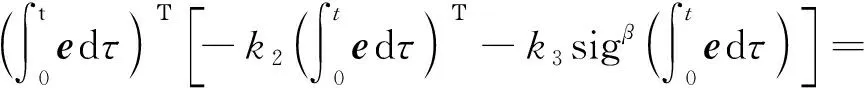
(14)

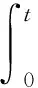
(15)

3.3 内环非奇异终端滑模控制器设计

下面基于滑模面(13)设计姿态控制器。

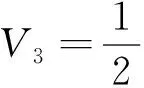
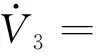
(16)

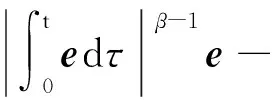
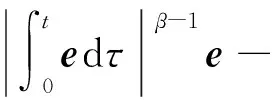
(17)

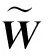
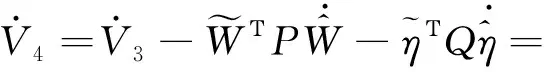
(18)

设计非奇异终端滑模双环跟踪自适应姿态控制器和自适应更新律为：

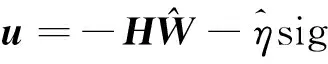
(19)

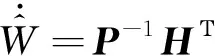
(20)

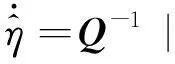
(21)

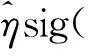
定理2：针对存在外部干扰的航天器动力学系统式(2)，姿态控制器式(19)和自适应律式(20)和(21)能保证系统式(2)渐近收敛到滑模面σ=0。

综合以上分析，可得到如下定理。

定理3： 航天器姿态动力学系统式(1)和(2)在姿态控制器式(19)和自适应律式(20)和(21)下全局渐近稳定，且当t→∞时，q(t)→0,ω(t)→0。

该证明过程同文献[15]。

注：当采用反演控制设计控制器时，需要构建Lyapunov函数V5=V1+V4，反演控制器为

(22)

式(22)比式(19)多了一项σ(σσΤ)-1(qΤe)。通过该项可以得到，在滑模面上时，控制力矩将达到∞。

4 仿真验证

航天器在完成对非合作目标的抓捕过程中，其转动惯量会从初始转动惯量J0开始，产生非线性摄动。其中摄动量ΔJ的变化特性可表示为[15]：

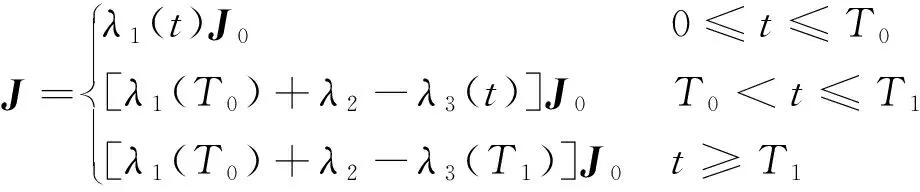
(23)

其中：λ1(t)为机械臂伸展过程中转动惯量增长速度。λ2为抓捕非合作目标后转动惯量突增比例，实际抓捕过程中，该参数未知，但有界。λ3(t)为机械臂回收过程中转动惯量递减速度。T0和T1分别为抓捕目标时间和完成机械臂回收时间。

外部干扰d为(单位：N·m，ωΔ=0.1)

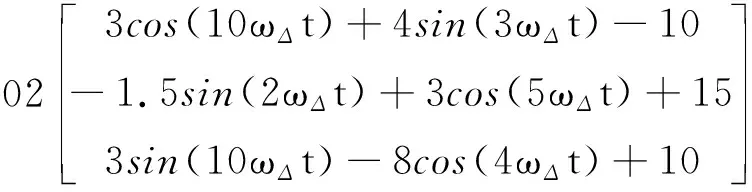
式中，3rectpuls(t-T0,0.1)表示航天器在抓捕非合作目标瞬间，受到非合作目标的反带动，会产生一个持续0.1s的瞬间方波强干扰。

采用ELM逼近中，隐层节点个数为6，激活函数为

仿真时间为80s，仿真参数见表1。

图2～5分别为航天器姿态角变化曲线、控制力矩曲线、实际角速度与预设虚拟角速度的变化曲线及滑模面的变化曲线。

图2显示，基于非奇异终端滑模双环跟踪姿态控制器，航天器的姿态角呈指数收敛到0。在第20s抓捕非合作目标的瞬间，被控系统出现0.1s的方波瞬态强干扰下，图3中的控制力矩有一个相对较大的波动，图5中的滑模面也在第20s有个突变，但姿态收敛轨迹没有发生任何改变，说明本文控制器能使抓捕航天器的姿态快速稳定，具有较强的鲁棒性和抗强干扰能力。

表1 航天器仿真参数

图2 姿态角变化趋势

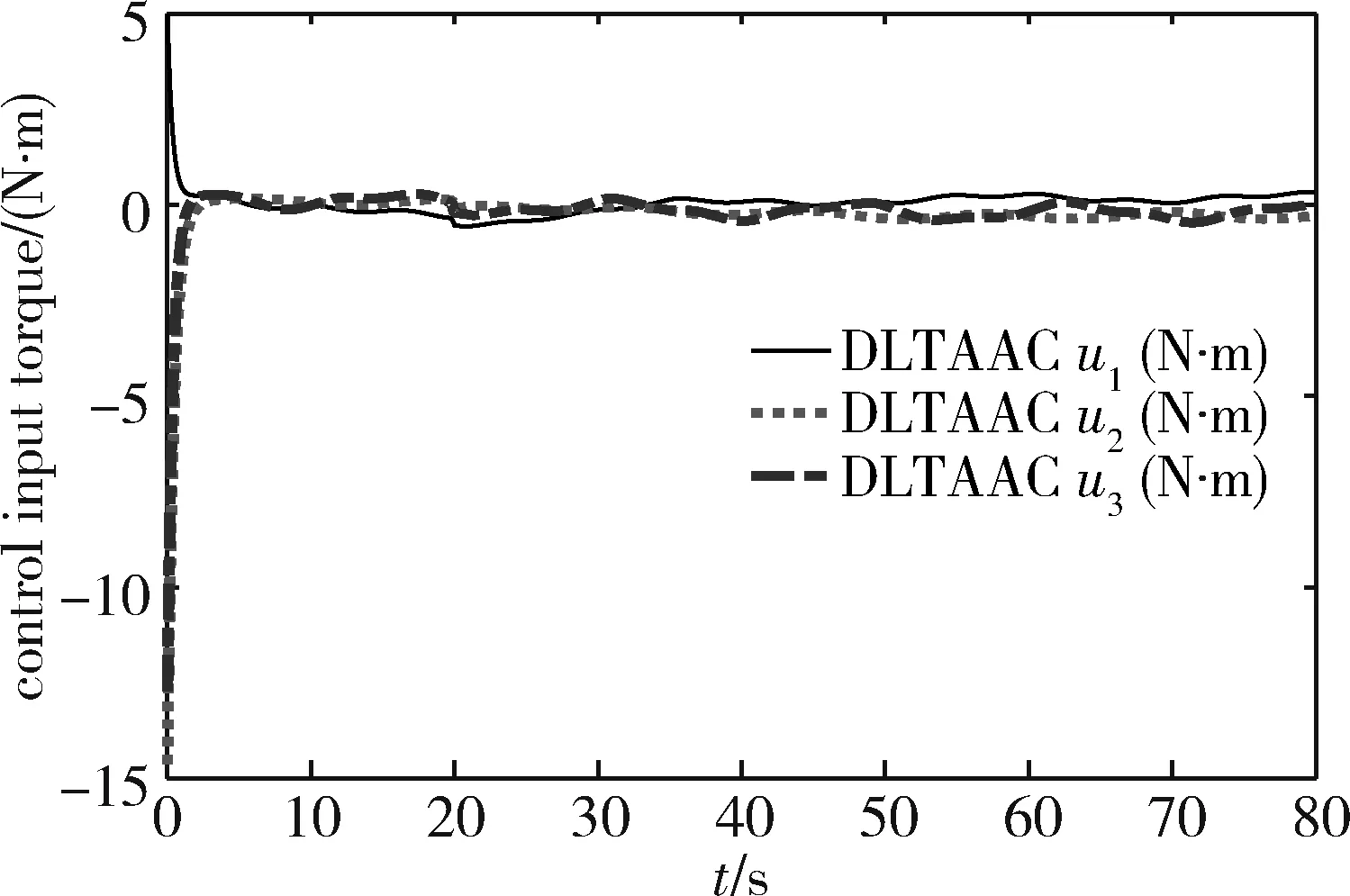
图3 控制力矩变化曲线

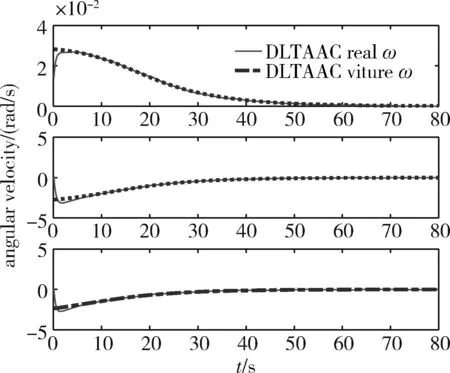
图4 ω和ωv轨迹曲线

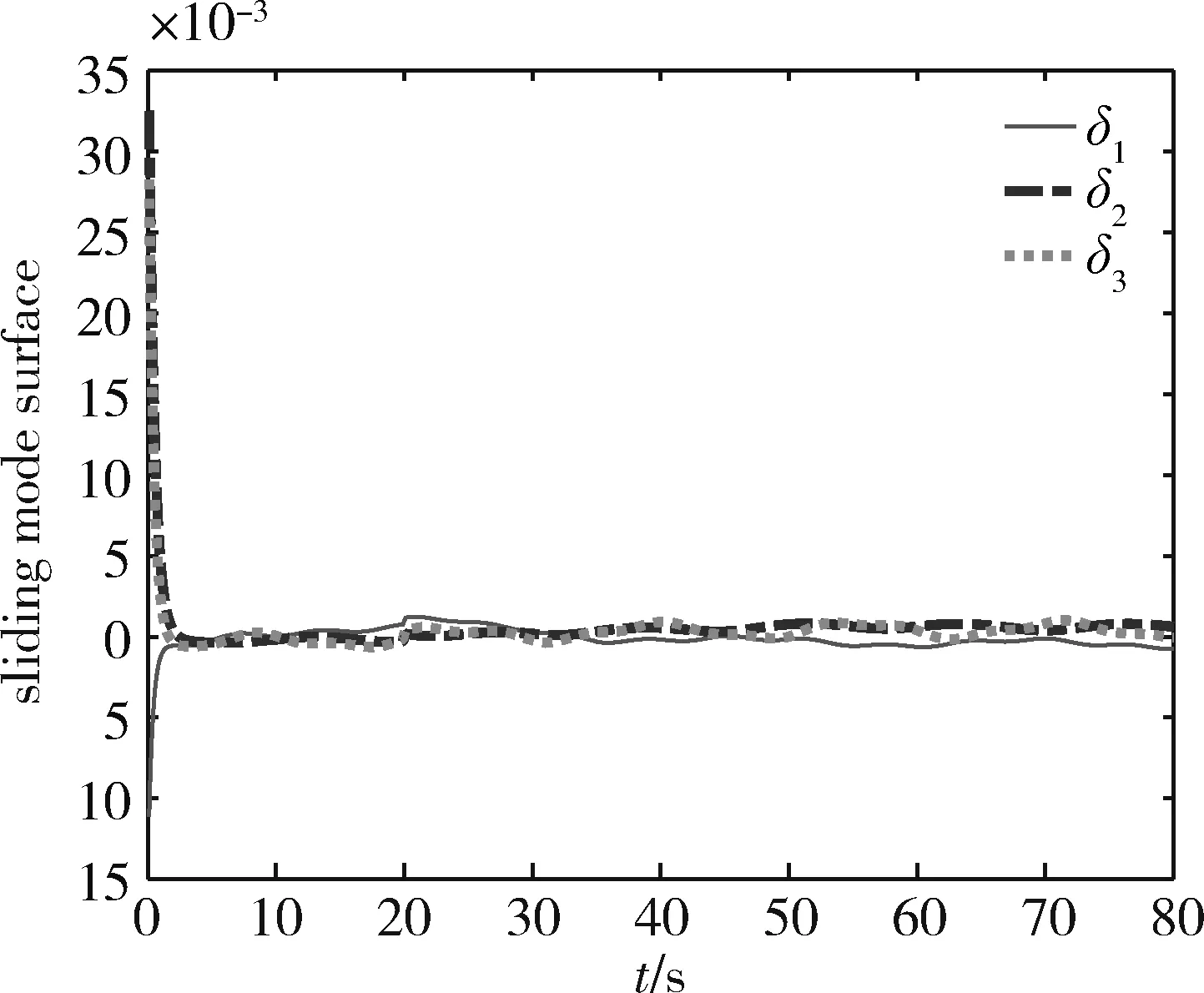
图5 滑模面的轨迹

5 结论

对存在转动惯量摄动、外部干扰和角速度有界约束的航天器姿态控制，给出了一种有限时间双环跟踪控制策略。

1)先对运动学方程预设有界虚拟角速度，并将该虚拟角速度作为动力学方程的期望轨迹，设计姿态控制器，使动力学方程的角速度输出在有限时间内精确跟踪上预设虚拟角速度，并按照虚拟角速度轨迹收敛到0，满足了航天器对角速度有界的物理约束；

2)构建了非奇异终端滑模面，当跟踪误差到达滑模面，其能在有限时间内收敛到0。基于非奇异终端滑模面设计了鲁棒姿态控制器，使实际角速度在有限时间内精确跟踪上期望角速度；

3)采用极限学习机技术对含未知转动惯量的部分进行逼近，设计自适应律估计逼近误差和外部环境干扰构成的复合干扰，增强了姿态控制器的鲁棒性，扩大了该控制器的使用范围。实际仿真结果显示，对瞬间产生的外部强干扰，该控制器也具有较好的控制效果。