基于无迹卡尔曼滤波的巡飞弹气动参数在线辨识方法

涂海峰 贾生伟 阳丰俊 吕 瑞

中国运载火箭技术研究院，北京100076

系统辨识是建立模型、改进模型以及验证仿真模型精度的重要手段[1]。依靠系统辨识，仅通过飞行试验中的输入输出观测信息就可获取系统的模型，其优势尤其体现在飞行器平台的开发上[1-5]。系统辨识可以代替风洞试验获取飞行器系统的气动参数，缩短设计周期，降低设计成本，因而被广泛应用于飞行器系统仿真平台搭建和控制器设计。对于追求低成本的巡飞弹药来说，如何通过系统辨识来获取巡飞弹药的气动参数，以减少研发成本，缩短研发周期是值得探索的问题。

经过多年的发展，已经发展出多种常用的系统辨识算法，按照参数获取的时间可分为离线辨识法和在线辨识法。其中，在线辨识法可以在线实时地估计模型参数，用于控制系统模型或参数在线修订，因而比离线辨识法得到了更为普遍的应用。在线辨识算法中扩展卡尔曼滤波(EKF)辨识算法是使用较多的方法。1971年，Chen、Eulrich等人[6]在研究报告中将EKF辨识方法应用于某垂直起降飞机的控制导数和稳定导数的辨识。之后的若干年中，Jategaonkar、Walker、Speyer和Chowdary等人[7-11]进一步研究了EKF辨识方法在飞行器气动参数估计中的应用。

虽然，EKF是目前针对非线性系统应用最为广泛的状态估计算法，但是它存在计算量大、估计精度低等缺陷[12-13]，同时部分复杂非线性系统很难求得系统的Jacobian矩阵和Hessian矩阵。为了避免这些问题，本文采用无迹卡尔曼滤波(UKF)实现飞行器的气动参数估计，并将该方法应用于巡飞弹药气动参数估计，通过与EKF气动参数辨识结果的对比分析，可知UKF在气动参数辨识方面优于EKF，实现气动参数的在线估计。

1 无迹卡尔曼滤波

UKF核心是通过一种非线性变换——无迹变换来进行非线性模型的状态与误差协方差的递推和更新。对于非线性问题，相比EKF，UKF至少为二阶近似，而且避免了计算系统的Jacobian矩阵和Hessian矩阵，拓展了适用于非线性系统的范围。

无迹变换(Unscented Tranformation，UT)是UKF算法的重要环节，其基本原理为：在原先状态分布中按某一规则取一些确定性的点集，称为Sigma点，来表征输入分布或部分统计特性，即使这些点的均值和协方差等于原状态分布的均值和协方差；参数化的采样点通过非线性变换进行传播，利用变换后变量的均值和协方差近似采样空间的均值和协方差[14]。因此UKF和EKF的区别如图1所示。

图1 实际采样、EKF近似与UKF近似的区别

(1)

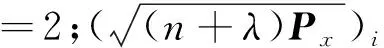
(2)

(3)

2 巡飞弹药气动参数辨识模型

飞行器的气动参数辨识过程中，为了便于分析，一般将纵向和侧向相关的气动参数分开辨识。纵向和侧向气动参数辨识所采用的方法相同，这里只对巡飞弹药纵向模型的气动参数进行辨识。当巡飞弹药在铅垂面运动时，便可得到辨识所用的巡飞弹药纵向非线性模型为：

(4)

式中,升力、阻力、俯仰力矩与攻角的计算公式如下：

(5)

D=CDQSw=QSw(CD0+CDosw(α-CDmin)2)

(6)

(7)

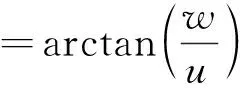
(8)

假设在飞行过程中没有风的干扰，则可用式(8)来计算攻角。另外，式(6)存在2阶项，对于最小二乘算法将是不可辨识的，需要对阻力系数的计算公式做如下变换：

D=CDQSw=QSw(CDα2α2+CDα1α+CDα0)

(9)

由式(5)到(7)可知，需要辨识的气动参数为CL0,CLα,CLδe,CLq,CDα2,CDα1,CDα0,Cm0,Cmα,Cmδe和Cmq共11个气动参数，这些参数构成待辨识参数向量θ为：

(10)

以上得到了巡飞弹药的纵向非线性模型，以及待辨识气动参数。下面将详述基于UKF的气动参数具体辨识过程。

3 基于UKF的巡飞弹药气动参数辨识

卡尔曼滤波只能实现状态的最优估计，要实现未知参数辨识，需要将待辨识的参数增广到状态向量中，有：

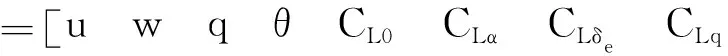
(11)

为了保证所有状态可观测性，其输出方程为：

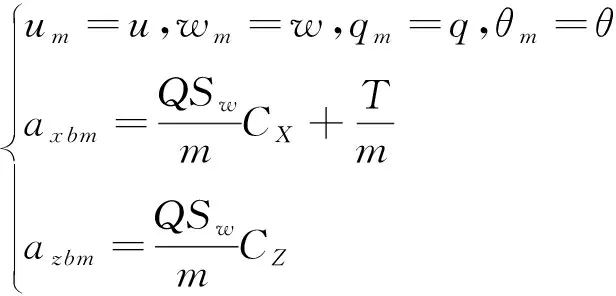
(12)

其中，CX和CZ分别表示在弹体坐标系下的气动力系数，其计算公式如下：

1)输入信号设计

为了实现参数的可辨识性需要设计控制输入以充分地激发辨识对象的动力学特性。输入信号设计的目的，就是设计飞行器执行机构的运动规律，使飞行试验过程可以激发出与待辨识参数相关的运动模态，为辨识提供足够的信息量。因此输入信号应尽量包含多种频率成分，满足要求的常用的输入信号有：阶跃输入、方波输入、偶极方波输入、“3211”多级方波输入、振荡型输入和闭环控制输入。

考虑到实际操作的简便性，同时为保证输入信息包含足够的频率以激发出纵向运动的所有模态，本文的输入信号选择为升降舵执行“3211”多级方波输入，其数学模型为：

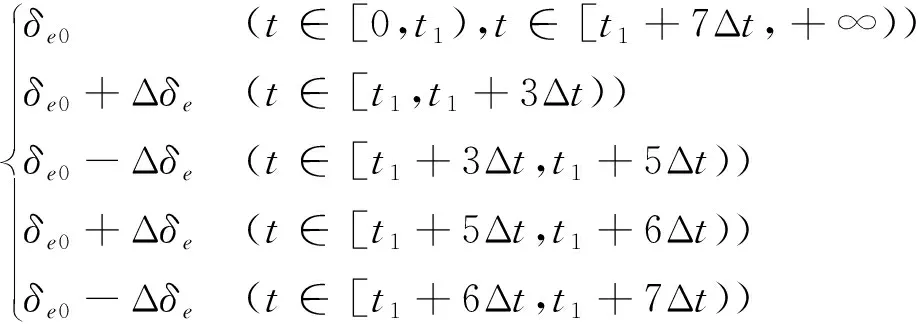
(13)

其中，Δt表示一个时间周期；δe0为平衡点处升降舵

输入；Δδe为“3211”输入的扰动量。为了充分地激发纵向运动短周期和长周期模态，升降舵采用如图2所示的控制指令输入，首先加入2个不同时间周期Δt不同扰动量Δδe的“3211”多级方波的信号，以激发短周期运动模态，然后加入一个周期较长的方波信号，以激发长周期运动模态。

2)辨识结果

将升降舵的信号输入到巡飞弹药六自由度非线性仿真平台中，其它输入如油门、方向舵和副翼则采用平衡点处的控制输入。EKF和UKF待辨识气动参数收敛情况如图3所示，气动参数的辨识结果如表1所示。

图2 升降舵的输入信号

图3 Hybrid EKF和UKF待估计参数收敛图

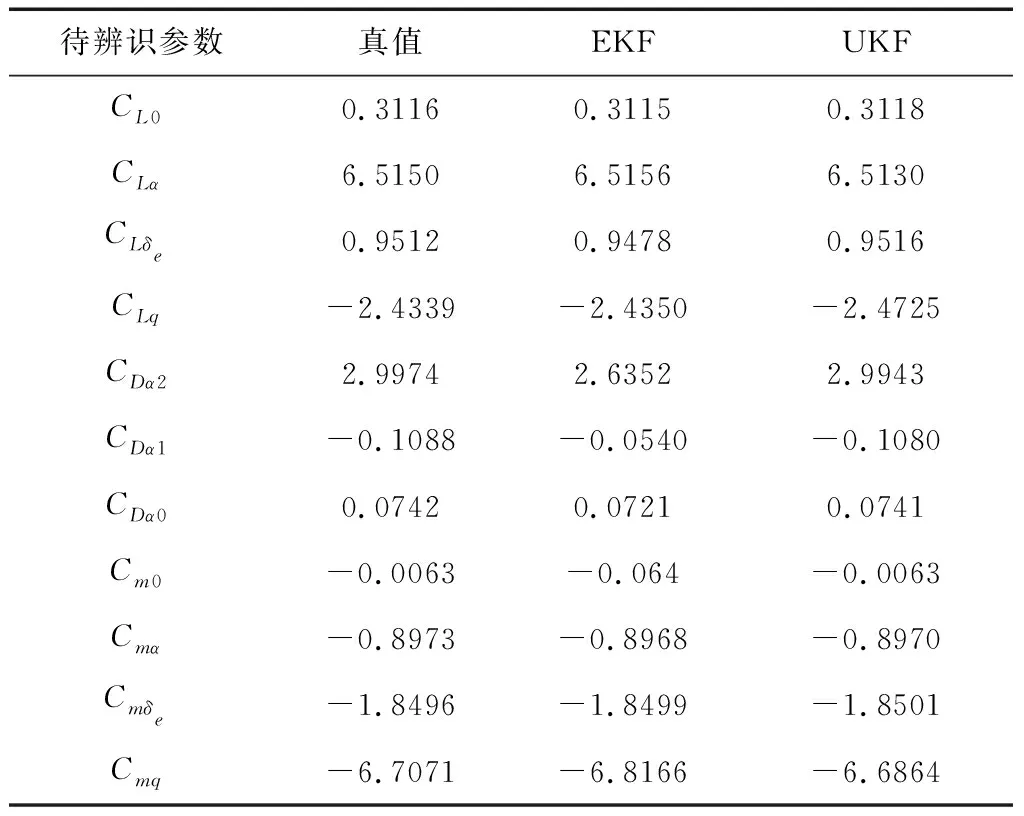
表1 参数辨识算法辨识结果对比

由图3和表1的对比结果可以看出，EKF和UKF在有控制激励输入的情况下，两者的收敛速度相当，然而对于阻力相关气动参数CDα0，CDα1和CDα2的收敛结果来看，UKF明显要比EKF算法更加接近于真值。因此可以得出对于在线辨识算法，UKF性能优于EKF。

4 结论

参数辨识能通过实际的飞行数据修正飞行器的气动参数，使得仿真所用模型更加准确，本文研究在线参数估计算法，采用UKF实现对非线性系统的在线参数辨识，相比于EKF，其辨识精度要更高，同时避免了求解Jacobian矩阵和Hessian矩阵的问题。通过巡飞弹药的仿真试验，验证了UKF在在线气动参数估计领域优于EKF。