基于观测器的线性离散信息融合预见控制算法
2018-11-01高春雷
高春雷 赵 宾,2 胡 洲
1.南京航空航天大学金城学院,南京211156 2. 南京航空航天大学自动化学院,南京211106 3. 四川航天系统工程研究所,成都 610100
最优控制的二次型性能指标函数中通常包含期望轨迹和控制能量的软约束信息,信息融合预见控制算法通过融合这些软约束信息以及系统状态方程和输出方程的硬约束信息,获得协状态和控制量的最优估计。文献[1~5]利用信息融合估计方法求解线性系统和非线性系统的最优控制问题。文献[6]针对期望轨迹和干扰可预见的最优跟踪问题,提出了一种基于误差系统的信息融合最优控制方法。文献[7]设计了欠驱动垂直起降飞行器悬停模式下的非线性信息融合控制方法,具有良好的控制效果和解耦性能。
信息融合控制算法本质上是一种基于状态反馈的最优控制方法,在利用该算法构建控制系统时需要引入全状态反馈。但在实际工程中,如吊车控制系统[8]、水面船舶控制系统[9]等的部分状态变量无法直接测量得到,导致以上方法在实际应用中都存在不同程度的局限性。针对这一问题,本文提出了基于观测器的线性离散信息融合预见控制算法,证明了在该算法中运用观测器设计状态反馈仍然具有分离特性。
1 线性非时变离散系统的可控可观性
线性非时变离散系统的状态方程式为:
x(k+1)=Ax(k)+Bu(k)
(1)
y(k)=Cx(k)+Du(k)
(2)
考虑状态反馈:u(k)=-Kx(k)+v(k),则在此反馈作用下,闭环系统为:
x(k+1)=(A-BK)x(k)+Bv(k)
(3)
针对系统(1)、(2)构造系统的观测器,即:
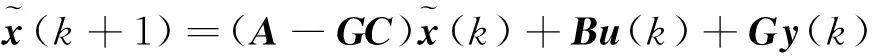
(4)
式中,x(k)是系统的n维状态;u(k)是m维输入;y(k)是实际系统的p维输出,k为离散时间;A,B,C,D为适当维度的常数矩阵;x(0)为系统初始状态,x(0)=x0。
引理1 对于式(1)和(2)所组成的线性非时变离散系统,若A为非奇异,则此系统用状态反馈(3)时能任意配置极点的充要条件是(A,B)能控,即rankU=rank[B,AB,…,An-1B]=n。如果A为奇异,则此仅为能控的充分条件[10]。
引理2 对于系统(1)和(2),若A为非奇异,状态观测器(4)存在的充要条件是(A,C)能观,即rankU=rank[C,ATCT,…,(An-1)TCT]T=n。如果A为奇异,则此仅为能观的充分条件[10]。
2 线性离散信息融合预见控制算法
对于系统(1)和(2),假设y*(k)表示p维期望输出向量。提出如下控制问题:求取某一控制律,使系统实际输出y(k)跟踪期望输出y*(k),并使得性能指标函数
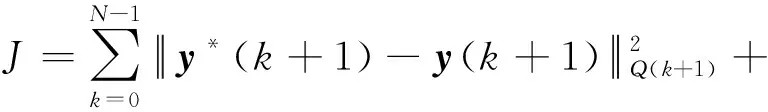
(5)
取值最小。式中,信息权重矩阵Q(k+1)∈Rp×p,R(k)∈Rm×m为对称正定阵[6]。控制量u(k)的最优融合估计为:

(6)
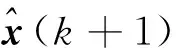
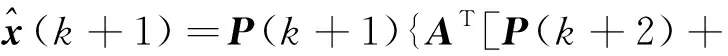
(7)

(8)
带观测器的信息融合预见控制系统框图如图1。

图1 带观测器的信息融合预见控制系统框图
3 状态观测器设计
假设系统(1)和(2)可观,构造观测器:
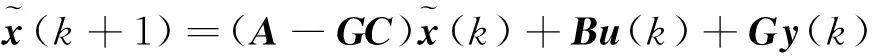
(9)
选择“反馈增益矩阵”G,使(4)稳定,即使A-GC的特征根全部在单位圆内。由此可得:
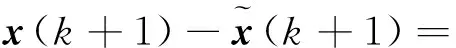
(10)
由于A-GC的特征根全部在单位圆内,所以式(5)稳定,即有:

(11)

(12)
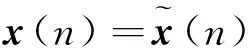
对于连续系统配置极点,极点越往左方远离虚轴,则系统越稳定,回到平衡位置的速度也越快。而对于离散系统,需要将极点配置在单位圆内,极点越靠近原点越稳定。通常将离散系统的所有极点直接配置在原点,以使所有状态估计值达到最快的收敛速度。

e(z)=zn+an-1zn-1+…+a1z+a0
(13)
由式(6)容易看出,该控制量的求取表达式是一个关于x(k)的全状态闭环反馈控制系统,由于本文所讨论的是基于观测器设计闭环反馈控制系统,则式(6)可变为

(14)

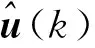
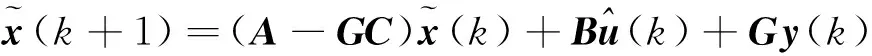
(15)
其中,y(k)为系统的输出信息,在实际系统中,即为传感器的量测信息。
4 分离特性证明
定理1 对于形如式(1)和(2)所表示线性离散信息融合预见控制系统,构造如式(4)所示的观测器,分离特性仍然成立。对于如式(6)所示的闭环状态反馈控制系统,其反馈状态由观测器估计状态替代后,仍然保留系统原有的性质。
证 由式(6)可表示为
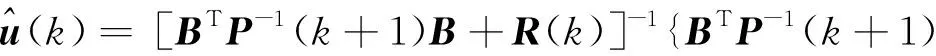
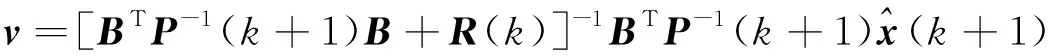
可得:
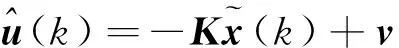
(16)
又由
y(k)=Cx(k)
(17)
将式(16)和(17)代入式(15)中,可得:
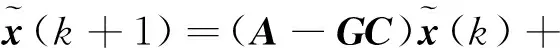
(18)
将式(16)代入式(1)中,可得:
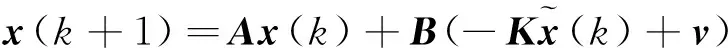
(19)
结合式(18)和(19),可得到增广系统方程如下:

(20)

(21)
式(21)表明,整个系统的特征多项式分别由(A-BK)和(A-GC)的特征多项式的乘积构成。因此,观测器的引入不影响由信息融合预见控制算法所配置的状态反馈系统的特征值λ(A-BK),而状态反馈也不影响观测器的特征值λ(A-GC)。由此可以得出,连续线性系统具有的分离特性,在线性离散信息融合预见控制系统中同样成立。证毕。
5 仿真实验
为了验证在信息融合控制中运用观测器的有效性,本小节通过吊车这一实际系统进行仿真实验。为了避免被控对象过于复杂,下面考虑一个典型的一维吊车系统的“摆动抑制控制问题”。根据文献[8,11],一维吊车系统的线性化动力学模型表示如下:



输出方程中包含小车的运动位置和负载的摆角,构造输出方程如下:

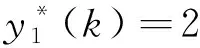

假设观测方程即为输出方程,小车的运动位置和负载摆角可直接测量。系统完全可观测,即:rankU=rank[C,ATCT,…,(A4-1)TCT]T=4,则存在:
使得A-GC的特征多项式(式13)为zn,代入A、C及相关的参数后求得:
为了清楚展现估计状态的收敛过程,图2~图5的仿真时间取为2s。从上面的4个图中可以看出,虽然仿真前仅假设了x2和x4的观测值包含初始误差,但在实际估计过程中,x1和x3的观测值也包含了误差。这是因为本文所采用的仿真模型是一个欠驱动系统,系统的各个状态间存在严重耦合,所以导致在估计的过程中x1和x3的观测值与真实值也会有所偏差,不过,这4个状态的观测误差在经过4步估计后就收敛到0了。
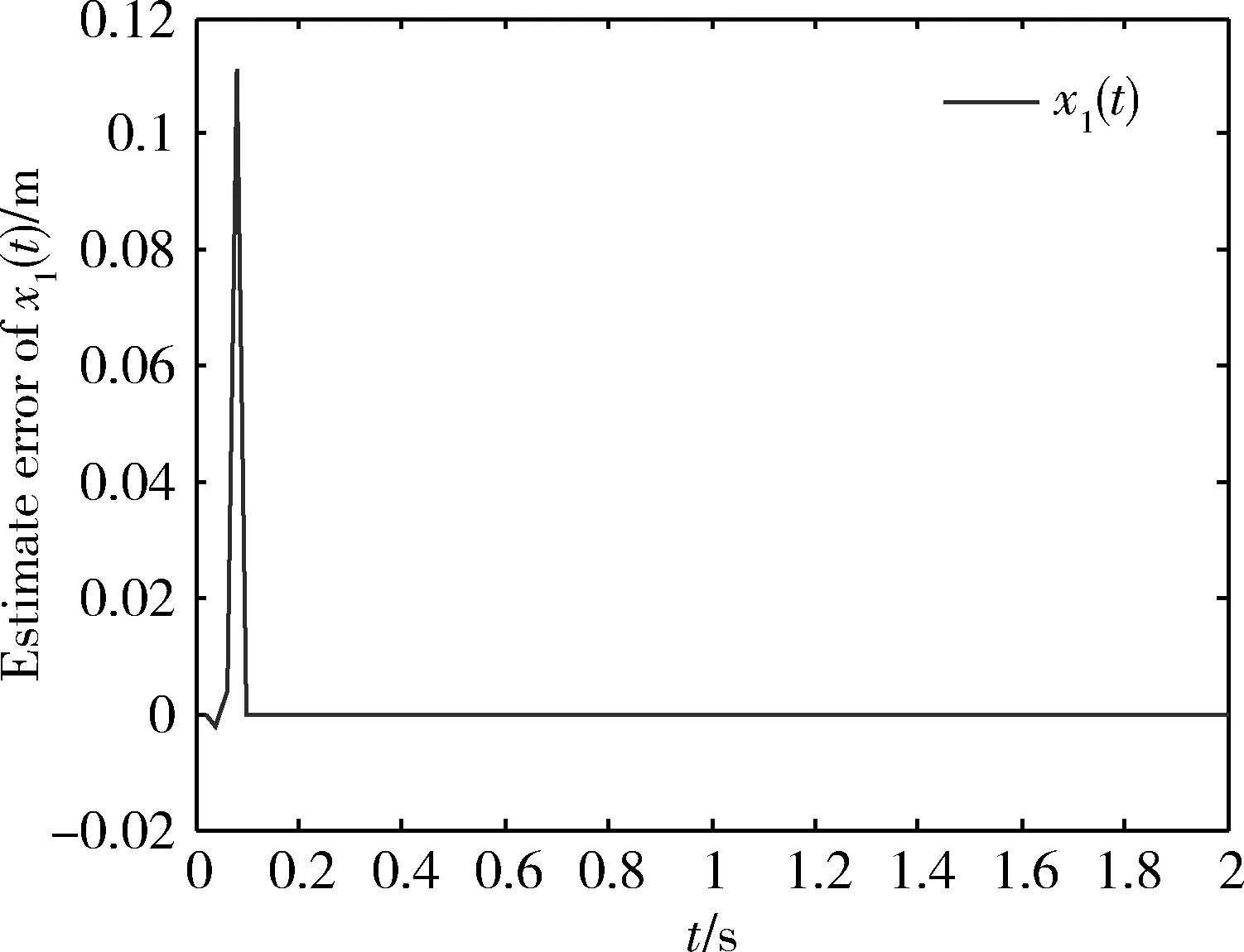
图2 吊车位置估计误差
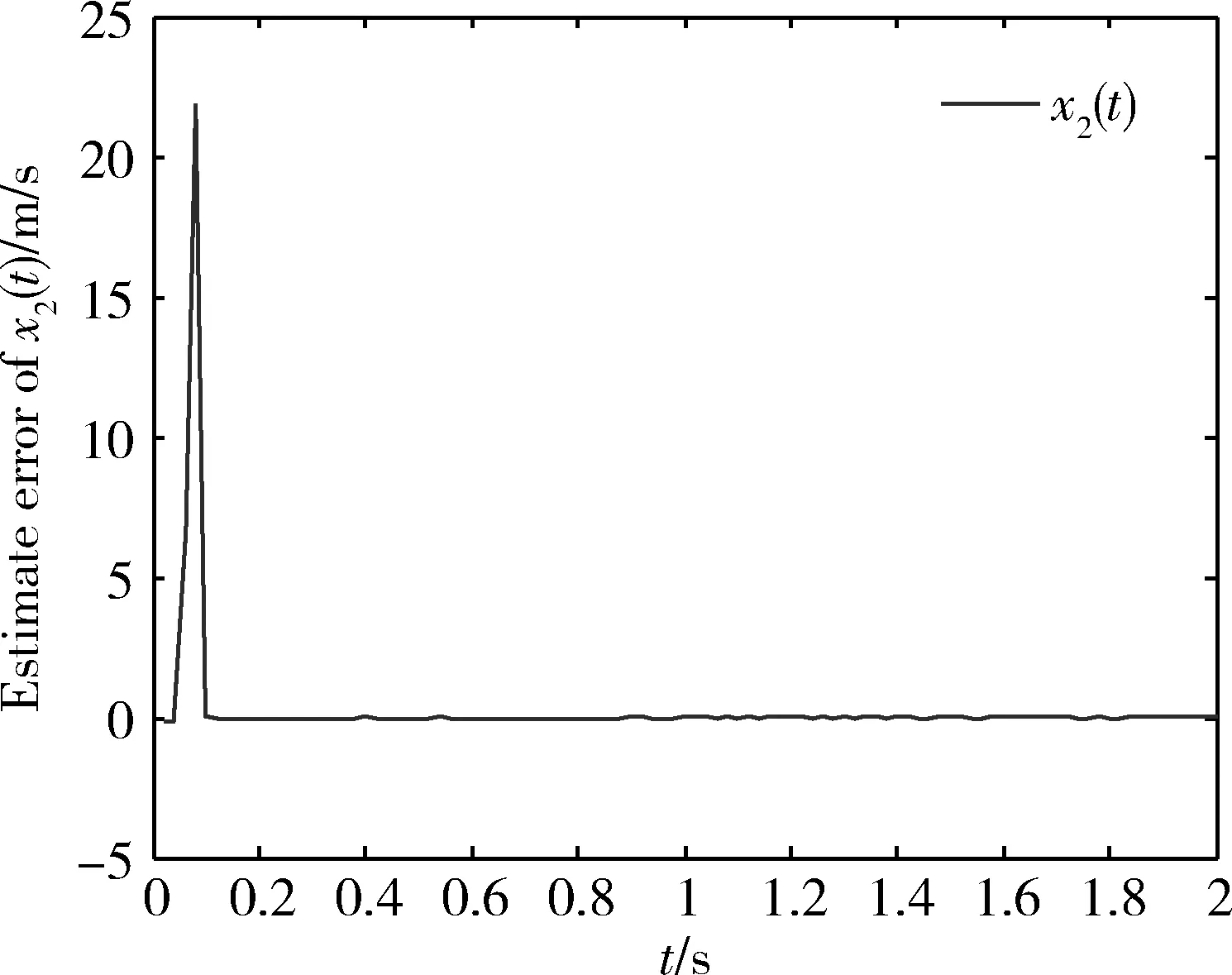
图3 吊车速度估计误差

图4 负载摆动角度估计误差
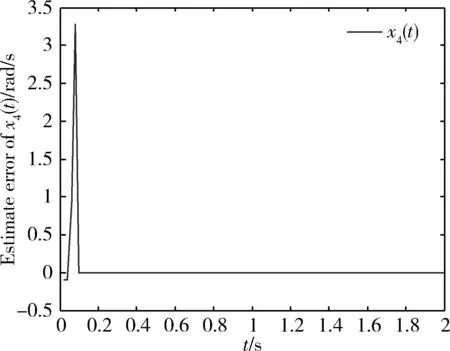
图5 负载摆动角速度估计误差
图6为吊车系统的小车位置跟踪和负载摆角跟踪误差曲线,由仿真结果可以看出在负载吊运过程中,吊车系统在5s左右同时实现了小车位置跟踪和摆角抑制。本文所采用的仿真对象模型及参数与文献[8]基本相同,文献[8]采用了部分反馈线性化方法,最后的仿真结果是吊车系统在7s左右同时实现了小车位置的跟踪和负载摆动的抑制。通过对比可以发现,本文所采用的方法具有更好的控制效果。
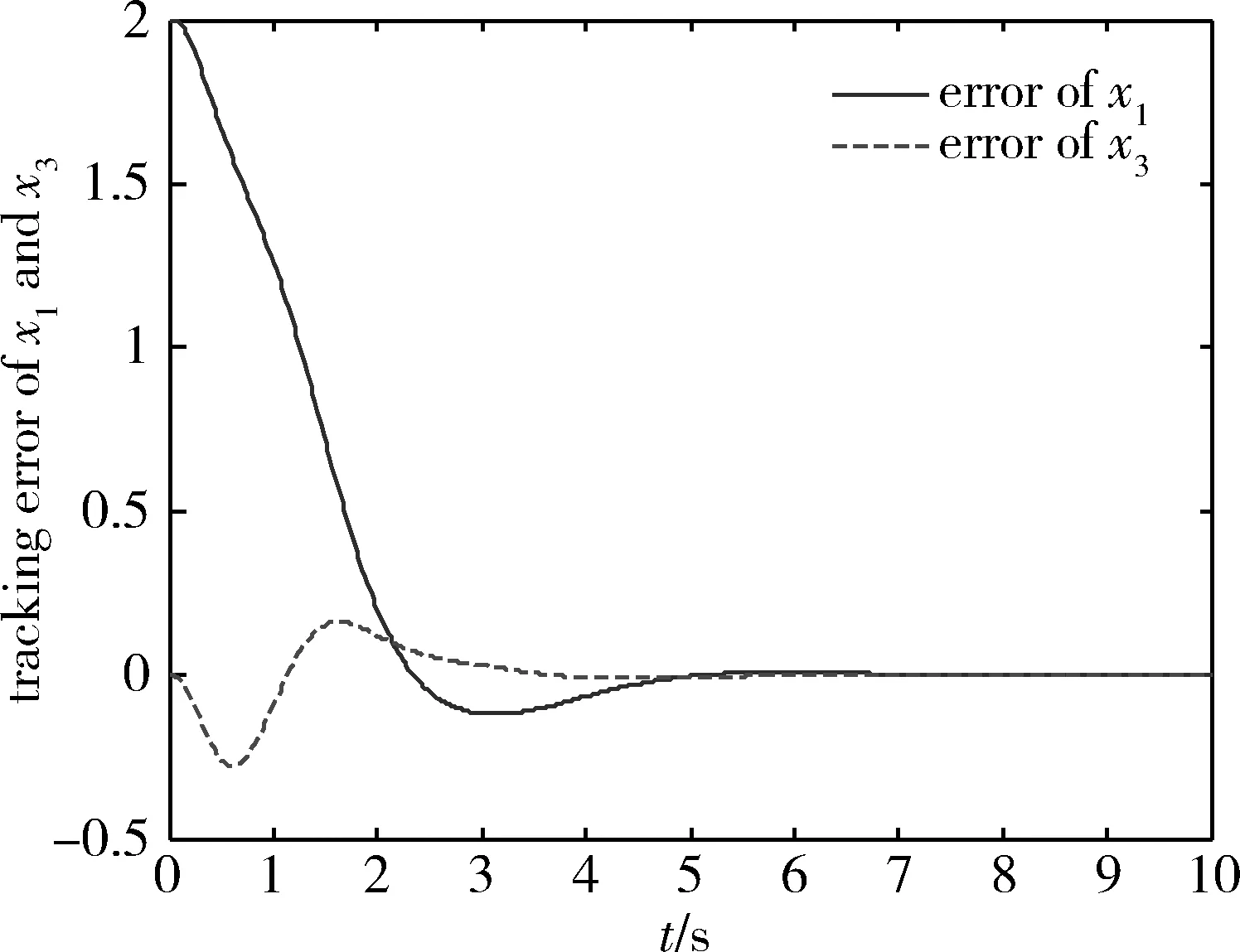
图6 小车位置和负载摆角的跟踪误差
6 结论
针对线性离散信息融合预见控制算法在实际应用中难以实现全状态反馈的问题,提出了一种基于离散观测器构建其全状态反馈的方法,并证明了对于利用观测器设计的线性离散信息融合预见反馈控制系统,分离特性仍然成立,在观测器的估计初值有误差的情况下,最多经过n步估计(n为系统的状态维数),观测误差就可以收敛到0。
