需求依赖库存水平的随机库存模型*

隆 冰 王 晶 朱军功

(重庆市交通规划研究院 重庆 400000)

0 引 言

库存管理是企业生产经营中一个不可或缺的重要组成部分，有效的库存管理方法可以调节供需平衡，减少货品余缺，提高库存效益，对实现价值链增值有重要意义.周卫琦等[1]在连续、均匀的需求假设下，考虑了订货批量的折扣现象，采用订货费、存贮费和缺货费描述库存费用，建立了有批量折扣且允许缺货的订货销售存贮模型.高海晶等[2]对供应商管理库存(VMI)模式下的单一制造商、单一零售商组成的二级供应链，以供应链收益最大为目标函数，分别在零售商总需求为常数和函数两种情况系建立了库存控制模型.刘诚等[3]考虑了具有价格弹性的随机零售商需求，并假设日需求量服从正态分布，在VMI模式下采用周期盘点的库存控制策略，以各零售商处的预期服务水平大于目标服务水平为约束，建立了分销系统利润优化模型.杨志林等[4]将库存成本描述为随存储时间变化的阶梯函数，考虑了需求率依赖于库存水平的需求函数，同时引入变化的订货费，建立了离散性库存费的库存控制模型.Timothy[5]提出了需求基于库存水平的库存模型灵敏度分析转换方法.Biswajit等[6]在需求函数基于库存水平的库存模型中，考虑了随时间变化的变质率，根据初始库存水平、当前库存水平、周期末端库存水平的关系建立了三种可能情况下的库存模型.Li等[7]在需求和需求预测误差服从随机分布的情况下或预测需求为单点和间断形式时，采用基于信任规则的库存控制方法对需求为非线性和非确定性的库存控制问题进行研究.欧剑等[8]在需求是随机的且依赖库存水平的条件下建立了订货模型，采用仿真的进化算法进行求解.贾湖等[9]建立了需求随机和供货时间随机的库存模型，假设了产品需求数量为一随机过程、补货时间相互独立、库存减少的数量为马尔代夫过程，基于此对基本库存进行了分析.

上述研究主要考虑了库存模型中需求函数的随机性以及需求与库存水平之间的关系，而缺乏对库存供给、需求、实时库存水平之间的联动关系考虑.本文同时考虑了基于即时库存水平下的库存供给方式，采用正态分布对需求随机项进行描述，并利用微分方程建立了需求、供给、当前库存量之间的联系；根据需求和库存水平的变化，分别描述了库存平衡、缺货、库存残余三种状态，提出了具有补货周期的随机库存模型.以库存系统效益最大为目标，以库存容量为约束，建立库存优化模型对库存周期和补货周期进行优化，最后进行了算例分析.

1 问题描述与模型假设

考虑库存需求随机波动下带有补货周期的库存系统，将库存成本描述为订货费、保管费、库存残余损失、缺货损失，在供货周期连续补货情况下，寻求库存系统效益最大化的库存周期和补货周期.库存模型假设如下：

假设库存模型存在一定的库存周期T和补货周期Tp，同时假设周期内的货品价值不随存储时间变化而在周期末的库存残余会瞬间贬值.在缺货期间假设库存为线性需求，缺货损失与缺货时长相关.库存费用由订货费D、保管费H、库存残余损失费O、缺货损失费B四部分组成.

1) 订货费 订货费由固定费用和附加费用两部分组成，周期内，假设固定费用与订货次数成正比，运输、装卸等附加费用与订货量成正比.

D=n·D0+k1·c

(1)

式中：D0为单次订货费用；n为订货次数；k1为订货附加费率；c为订货量.

2) 保管费 保管费与库存周期内的实时库存量成正比.

(2)

式中：k2为保管费率；ct为t时刻的实时库存量.

3) 库存残余损失费 库存残余损失费由残余货品的订货费、保管费、货品贬值损失组成.

O=k1·Cs+k2·T·Cs+k3·Cs

(3)

式中：Cs为残余库存量；k3为单位货品贬值损失费用.

4) 缺货损失费 缺货损失费与库存周期内的实时缺货数量成正比.

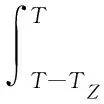
(4)

式中：Tz为库存周期内的缺货时长；kt为单位货品的缺货损失费用；zt为t时刻的实时缺货量.

2 带有补货周期的随机库存模型

传统库存模型假设需求函数为线性，即在整个库存周期内，货品的需求保持恒定水平.线性需求假设忽略了需求的波动以及需求对库存的依赖.模型假设需求为带有随机项的关于实时库存水平ct的函数.

q(t)=f(ct)+ε

(5)

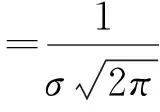
库存供给一般有一次补齐和连续补货两种方式，一次补齐方式是在每个库存周期内将货品一次性补充到同一库存量；连续补货方式则是在补货周期内结合库存水平连续补货，模型假设供给为关于库存水平的函数.

p(t)=φ(ct)

(6)

需求和供给函数的叠加又直接决定了库存水平的变化.

(7)

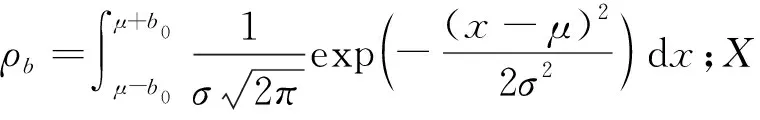
1) 一次补齐库存概率模型 对于一次性补齐库存模型，由于需求函数中随即项ε的作用，会出现缺货和库存残余，见图1，在每个库存周期将货品一次性补充到同一库存量C，考虑周期内的需求的随机波动，利用平衡balance、缺货shortage、残余residue三种情况下的库存成本期望值对库存成本进行描述.

图1 一次补齐库存概率模型

周期内的订货费：Db=D0+k1·C；Ds=D0+k1·(C+r.Tz)；Dr=D0+k1·(C-Cs).

周期内的库存残余损失费：Ob=0；Os=0；Or=k1·Cs+k2·T·Cs+k3·Cs.

按照balance、shortage、residue出现的概率分别为ρb，ρs，ρr，则库存成本可以用其期望值加以描述.

·ρi

(8)

2) 整周期连续补货库存模型 整周期连续补货库存模型可以按照当前库存量进行补货，可以将库存量维持在一个相对稳定的水平，但连续进货同时也造成了较大的订货成本.

整周期连续补货可以忽略库存残余损失和缺货损失，则整周期连续补货库存模型总成本为

Cost2=D+H

(9)

3) 带补货周期的随机库存模型 连续补货则可以根据当前库存调节补货量，将库存保持在一个低而稳定的范围，考虑到整周期连续补货订货成本太高，只在整个库存周期中的部分时段补货，从而形成补货周期Tp，随着补货周期的延长，缺货和残余的概率将逐渐降低.综合一次补齐模型和整周期连续补货模型，得到图2的带补货周期连续库存模型.

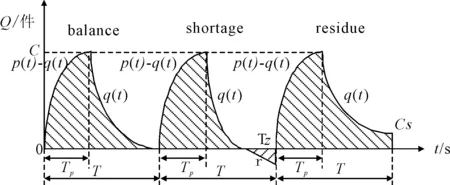
图2 带补货周期的随机库存模型

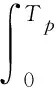
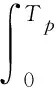
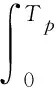
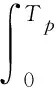
周期内库存残余损失费：Ob=0；Os=0；Or=k1·Cs+k2·T·Cs+k3·Cs.

结合历史数据统计，对随机项ε的期望值μ取正、负值的概率进行估计，分别取值为ρ1，ρ2，ρ1+ρ2=1，对于μ取正值时，可分别计算正偏离下的平衡balance、缺货shortage、残余residue状态下的概率ρ1b，ρ1s，ρ1r；μ取负值时，可分别计算负偏离下的平衡balance、缺货shortage、残余residue状态下的概率ρ2b，ρ2s，ρ2r；利用各种状态下的库存成本的期望值对周期内的库存成本为

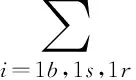
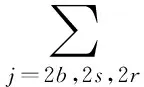
(10)

假设库存消耗产生的收益与库存消耗量成正比，单位库存消耗量产生效益为ω.则利用期望描述周期内的库存效益为

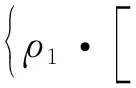
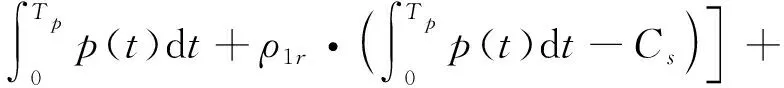
(11)

p(t)=φ(c(t))

(12)

期望值对随机需求为

q(t)=

供给累计和需求消耗对库存水平为

c(t)=

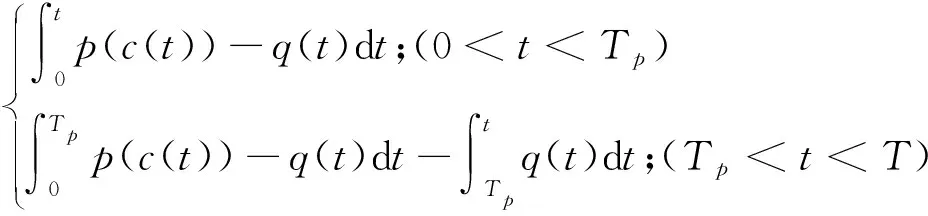
(14)

式中：ρ1b+ρ1s+ρ1r=1，ρ2b+ρ2s+ρ2r=1，ρ1+ρ2=1.

将随机项ε的期望值μ描述为与供货周期和库存周期相关的函数为

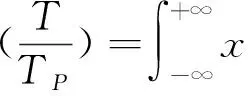
(15)

得到库存效益模型为

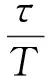
(16)

(17)

式中：目标函数为τ时间段内库存效益最大；T，Tp为决策变量；Cmax为最大库存容量；Cmin为安全库存容量，

通过模型求解，得到库存系统效益最优的库存周期To和补货周期Tpo，由此可以得到周期内的订货量Co，最高库存水平Cmax.

(18)

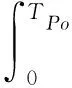
(19)

3 模型求解

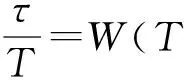
(20)

按照式(14)的简化，通过如下迭代步骤逐步逼近式(10)的最优解：

步骤1初始化count=0，设初始可行解为(T0,Tp0)，定义T=(T，TP).

步骤2count=count+1.

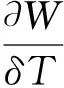
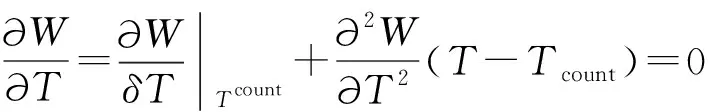
步骤5收敛判断，定义gap=|W(Tcount)-W(Tcount-1)|.若Tcount满足收敛准则，停止迭代，返回Tcount；否则返回步骤2.

4 算例分析

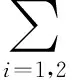
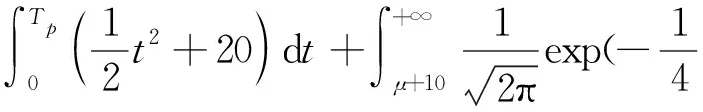
(21)

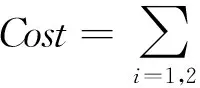
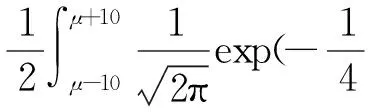
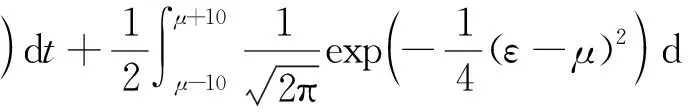
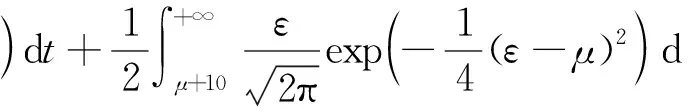
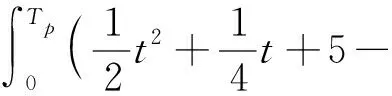
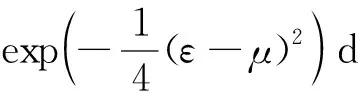
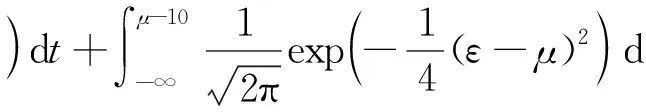
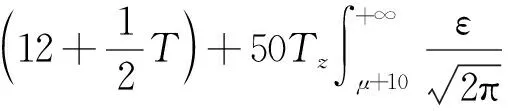
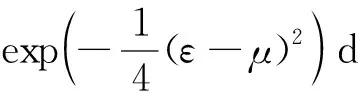
(22)

(23)

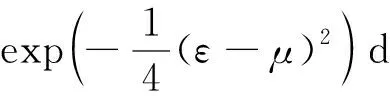
(24)

将Cost,E,Cs,Tz带入式(16)、(17)求解得到：Tp=11 d，T=42 d.订货总量为421件，最大库存量为286件.从上述结果可以看出，带有补货周期的库存模型相对于一次补齐模型，最大库存量减少了135件，节约了32%的库存容量.

同时考虑到现实订货商为了保障生产和销售的连续性，往往对库存消耗预期偏高，降低残余库存损失具有现实意义，连续补货利于订货商捕捉周期内的需求规律，减少缺货和库存残余，对提高库存系统总效益有积极意义.

5 结 束 语

针对库存需求和供给依赖于库存水平的库存系统，在需求函数随机项波动服从正态分布的假设下，描述了库存系统供需平衡、库存残余、缺货三种状态；并利用库存成本期望建立了带有补货周期的随机库存模型；以库存系统总效益最大为目标函数建立优化模型对补货周期和库存周期进行优化，计算了库存系统周期内的订货量和最高库存水平.模型反映了即时库存水平对库存供给和需求的调节作用，更符合实际；考虑补货周期在库存周期内对需求随机波动范围的影响，体现了供给、需求、即时库存水平之间的平衡反馈机制；模型求解了系统最优下的补货周期和库存周期，为指导连续生产提供了理论基础，模型求解的最优订货批量和最大库存量对优化库存系统，节约库存成本具有积极意义，可变的补货周期丰富了模型的拓展性和适用空间.本文只针对特定属性的货品进行研究，对于货品构成复杂的混合库存系统还有待进一步研究.