拱桥钢箱吊杆驰振稳定性数值计算研究*

詹 昊 廖海黎

(西南交通大学土木工程学院1) 成都 610031) (中铁大桥勘测设计院集团有限公司2) 武汉 430056)

0 引 言

通常驰振是细长结构在横风向作用下的一种不稳定的单自由度发散振动现象，会导致结构破坏.对于桥梁结构，驰振易发生在拱桥吊杆、桥塔这类阻尼较小的细长结构上.由于驰振具有很大的破坏性，应采取措施尽力避免驰振发生，使驰振临界风速高于驰振检验风速.对于不同切角形状的正方形和长方形截面的气动力性能研究相对较少，且多为静态绕流研究，可以参见文献[1-4]的风洞实验结果及文献[5]的数值仿真计算结果.对于驰振问题的数值计算主要有两种方法.方法一，首先通过计算流体方法求出不同风攻角下的阻力系数和升力系数，再根据葛劳渥-登哈托原理判断驰振是否发生，用相关公式计算驰振临界风速.方法二，建立流固耦合数值计算模型直接吹出驰振临界风速.从相关文献来看，多用方法一进行研究，运用方法二进行研究相对较少[6].

本文通过两种方法对横桥向来风时，南京大胜关大桥吊杆进行驰振数值仿真计算分析，并对其截面进行优化.两种方法相互验证，与风洞实验结果进行对比分析.并展示了驰振中的极限环振动现象.

1 工程概况

南京大胜关桥为双线高速和双线I级干线铁路桥梁，主桥采用6跨连续钢桁拱桥，三桁承重结构.大桥吊杆采用钢箱型截面，最长吊杆长度超过50 m，柔度大，发生驰振的可能性大.对于拱桥吊杆的风致振动制振措施一般是改变吊杆气动外形的空气动力学措施和设置阻尼器的机械措施.机械措施所需成本及后期维护费用很高；截面形状的微小变化往往会改变结构的气动性能，在保证吊杆安全的情况下，改变吊杆气动外形的气动力学措施几乎无需增加成本，因此，吊杆截面选型显得十分重要.南京大胜关大桥三种截面方案见图1，计算参数为表1.

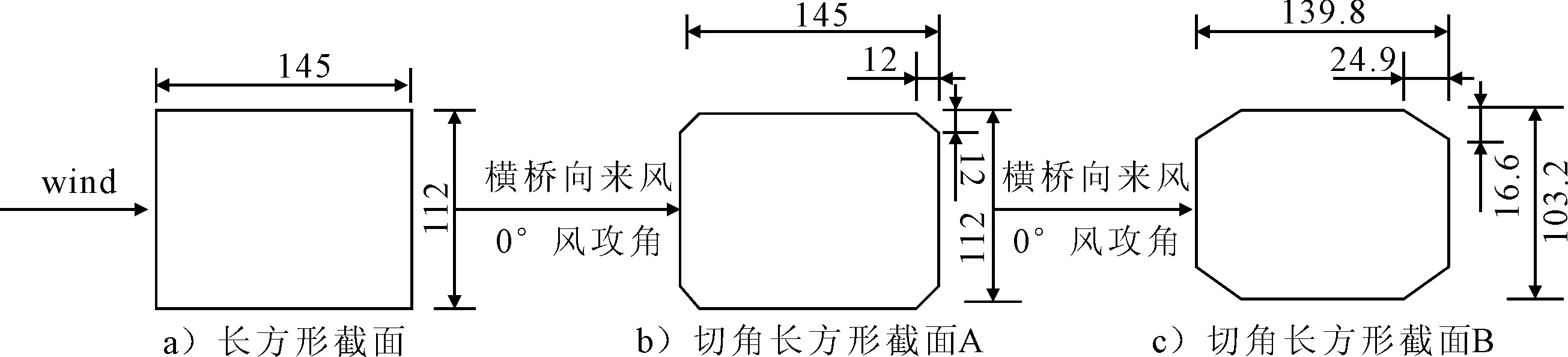
图1 三种方案截面图 (单位：mm)

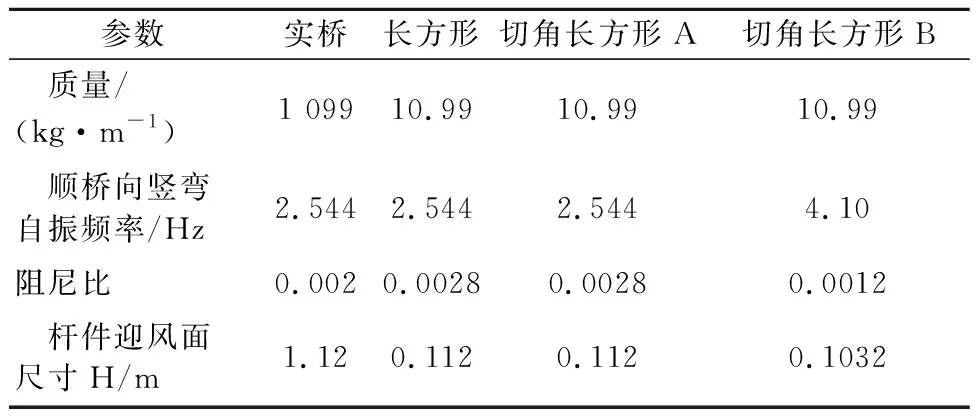
参数实桥长方形切角长方形A切角长方形B 质量/(kg·m-1)1 09910.9910.9910.99 顺桥向竖弯自振频率/Hz2.5442.5442.5444.10阻尼比0.0020.00280.00280.0012 杆件迎风面尺寸H/m1.120.1120.1120.1032

2 方法一

2.1 数值仿真计算原理

风轴坐标系下的阻力、升力和升力矩系数分别为

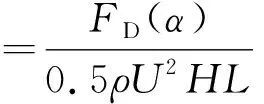
(1)

(2)

(3)

式中：0.5ρU2为气流动压；L为节段模型的长度；FD(α)，FL(α)和MZ(α)分别为攻角α情况下采用风轴坐标系时的阻力、升力和俯仰力矩；H为结构高度.

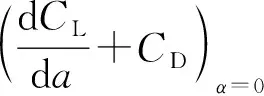
驰振临界风速为

(4)

式中：m，ζ和ω分别为结构的质量，阻尼比和角频率；H为结构高度；ρ为流体密度，空气密度常温时取1.225 kg/m3.

2.2 数值仿真计算模型

长方切角B截面网格划分图见图2，其他两种截面网格划分与长方形截面相似.整个流场网格由三部分构成，包围截面的边界层结构网格区域，非结构网格过渡区域和最外面的结构网格区域.动网格变形采用动态分层法.风向从左至右，左侧设定为速度入口，右侧设定为自由出流.上下边界为无滑移固壁边界.矩形计算区域为3.3 m×3 m，模型上游来流区域为0.8 m，下游尾流区为2.5 m，离上下边界各为1.5 m.数值计算中，采用有限体积法求解，其中对流项采用二阶迎风差分格式，压力和速度的耦合采用SMPLEC算法.RNGk-ε湍流模型对于有较大速度梯度的流场及分离流计算较准确，计算时间适中，本文计算采用RNGk-ε湍流模型.

图2 计算网格划分

2.3 数值仿真计算结果

横桥向来风时，阻力系数CD和升力系数CL随风攻角α变化曲线图见图3～4.

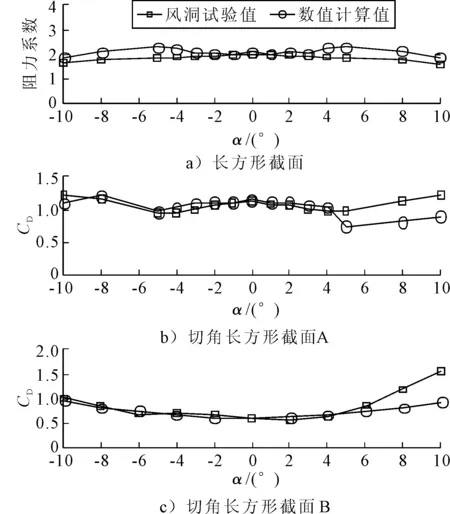
图3 阻力系数随风攻角变化曲线(U=10 m/s)

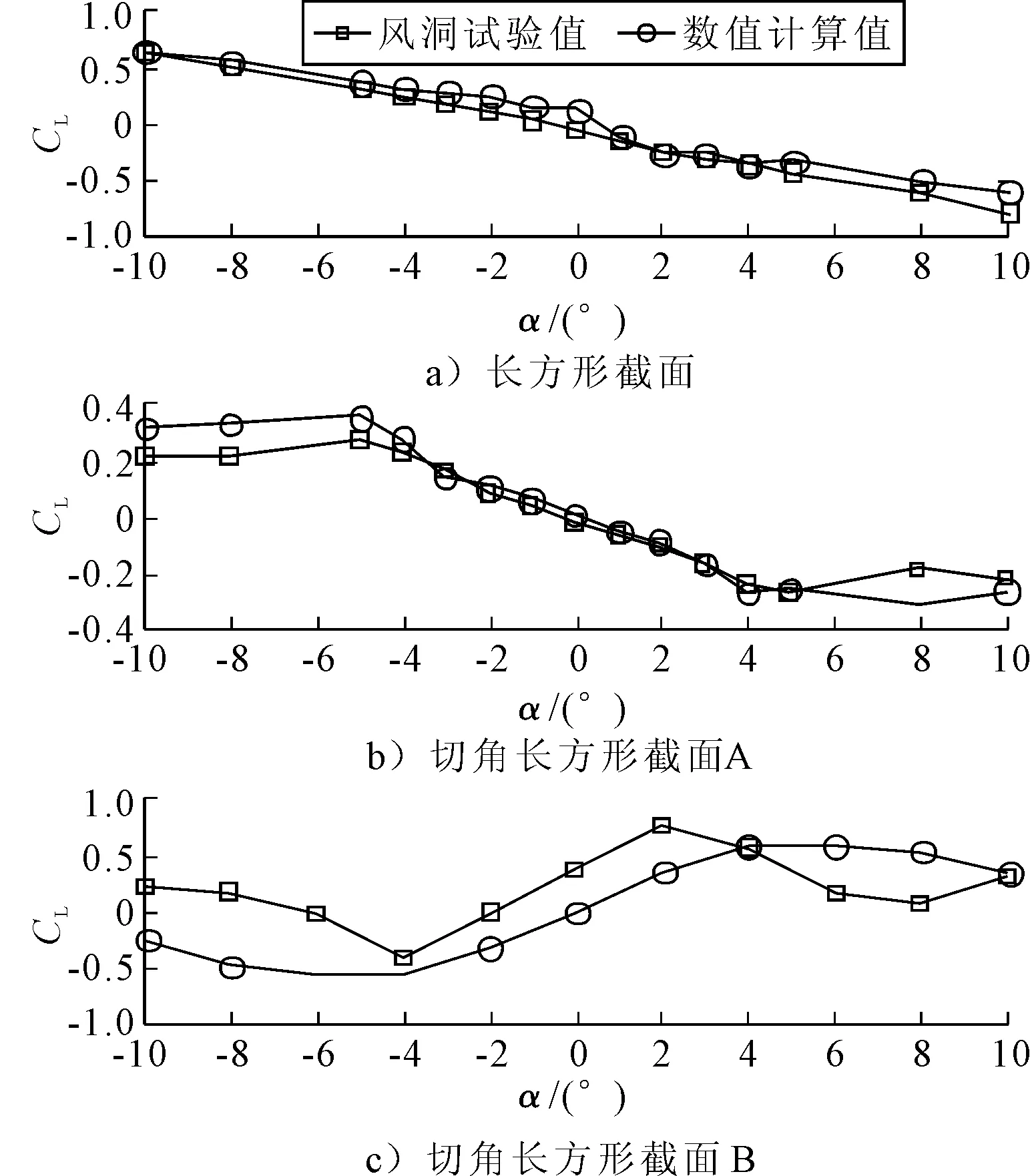
图4 升力系数随风攻角变化曲线(U=10 m/s)

由图3～4可知，CD大致以0°风攻角为中心对称分布，CL大致以0°风攻角为中心反对称分布.长方形截面CD计算值大于风洞试验值，CL计算值和风洞试验值吻合较好；切角长方形截面A的CL和CD计算值和风洞试验值吻合较好；切角长方形截面BCD和风洞试验值吻合较好，CL数值计算值和风洞试验值有所差别，但变化趋势基本一致.根据驰振临界风速公式计算的结果见表2.

由表2可知，驰振力系数和风洞试验基本吻合，通过式(4)计算得到的驰振临界风速两者基本吻合.横桥向来风时，实际桥梁最长吊杆中间高度的驰振检验风速为50.4 m/s，长方形截面和长方形截面A不能满足驰振要求.长方形截面B由于驰振力系数为正数，不会发生驰振.

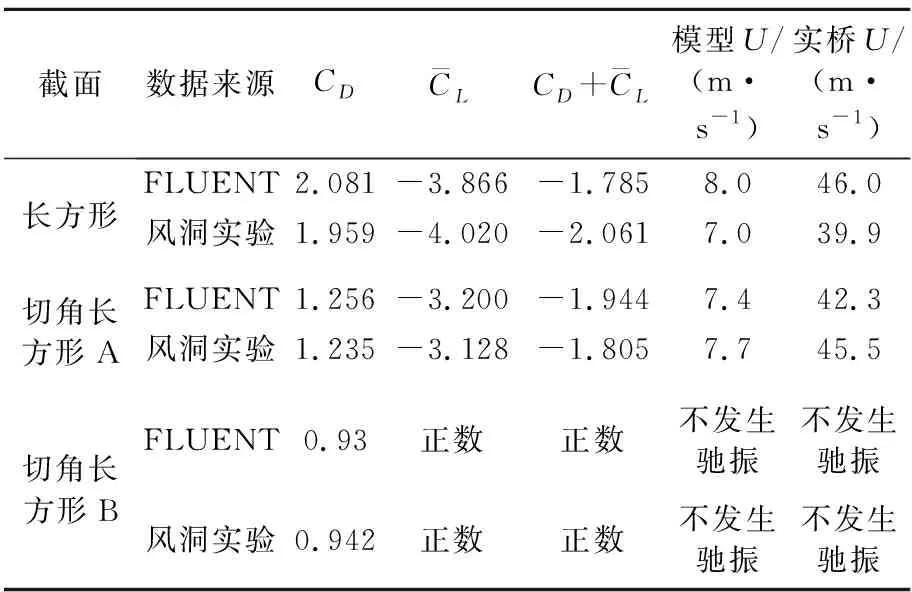
表2 方法1计算结果

3 方法二

3.1 数值仿真计算原理

将吊杆简化成质量弹簧阻尼系统，建立竖向弯曲流固耦合模型，数值仿真计算原理示意图见图5[7-8].

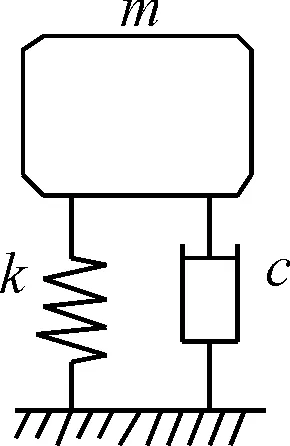
图5 数值仿真计算原理示意

(5)

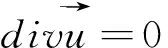
(6)

式中：m为结构的质量；kh为竖弯惯性矩；kh为竖向刚度；ch为结构阻尼；Fh为竖向气动力；y为物体竖向位移.

对于不可压缩流体的连续方程和纳维-斯脱克斯方程为

(7)

用FLUENT软件求解流体控制方程式(6)～(7)，得到吊杆周围流体的速度场和压力场以及作用在柱体上的升力.将Newmark方法的代码嵌入用户自定义函数(UDF)同软件连接，通过UDF来提取升力代入吊杆振动方程(2)，求解吊杆的动力响应.然后将吊杆的速度通过FLUENT的动网格技术进行传递使网格获得速度.最后用速度与时间步相乘来得到网格位置的更新，开始下一个时间步计算.如此循环得到各时间步的振动位移.计算网格划分同方法1.

3.2 数值仿真计算结果

各截面方案旋涡脱落见图6，不同风速下长方形截面A位移时程曲线见图7.

图6 旋涡脱落图(U=10 m/s)

由图6可知，长方形截面切角后，旋涡脱落强度减小，其中切角长方形截面B的涡脱落强度最小.

图7 不同风速下吊杆位移时程曲线(切角长方形截面A)

由图7可知，U=7 m/s，竖向振幅很小，不到1 mm；U=8.0m/s，竖向振幅突然增大，达到了65 mm；随着风速的增大，竖向振幅继续增大，最后稳定在一个极限振幅上.与涡激共振不同，驰振没有锁定风速区间，其振幅随着风速的增大而增大，且比涡激共振振幅大得多，达到杆件截面尺寸数倍.不同风速下长方形截面和切角长方形截面A最大振幅见表3～4.

表3 不同风速下最大振幅(长方形截面)

H=11.2 cm，为杆件迎风面高度.

表4 不同风速下最大振幅(切角长方形截面A)

以结构振幅开始迅速增大时的风速作为驰振临界风速，由表3～4可知，长方形截面驰振临界风速为7.5～8.5 m/s, 切角长方形截面A驰振临界风速为7～8 m/s，切角长方形截面B在各级风速下振幅没有超过2 mm，没有发生驰振.方法二计算结果与风洞试验值对比见表5，节段模型风洞试验采用直接吹出驰振临界风速.方法一计算结果见表6，两种方法计算结果和风洞实验基本吻合.

表5 方法二计算结果

表6 方法一计算结果

风速U=16m/s时，切角长方形截面A不同时间段的升力系数时程曲线及对应的功率谱密度函数分别见图8～9，升力系数功率谱密度曲线峰值对应的横坐标为旋涡脱落频率值.

0～35 s是杆件静止到振动到达稳态的整个过程：其中0～5 s是杆件从静止到开始振动；17.5～35 s是物体振动达到稳定状态，其中30～32 s是稳态中的一段放大图像.由图8可知，0～5 s时，涡脱落频率f=27 Hz，这与截面静止绕流时的涡脱落频率相同.17.5～35 s时物体振动达到稳定状态，由于物体大幅度振动，对涡脱落频率有调整作用，涡脱落频率和物体的固有频率趋向一致，这与文献[9-10]中的结论一致.升力系数曲线大的波动周期与物体的固有频律相近，杆件的固有频率是2.544 Hz，此时主要旋涡脱落频率f=2.5 Hz.同时还存在3倍、5倍、10倍和15倍的次要频率，即存在f=7.5，12.5，22.5，27.5 Hz的涡脱落频率.方法二的计算结果见表5. 当V=24 m/s，切角长方形截面A相轨迹见图10.

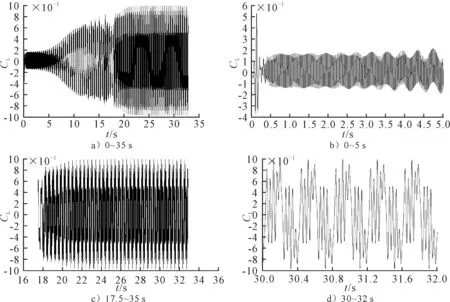
图8 不同时间段的升力系数时程曲线(切角长方形截面A,V=16 m/s)

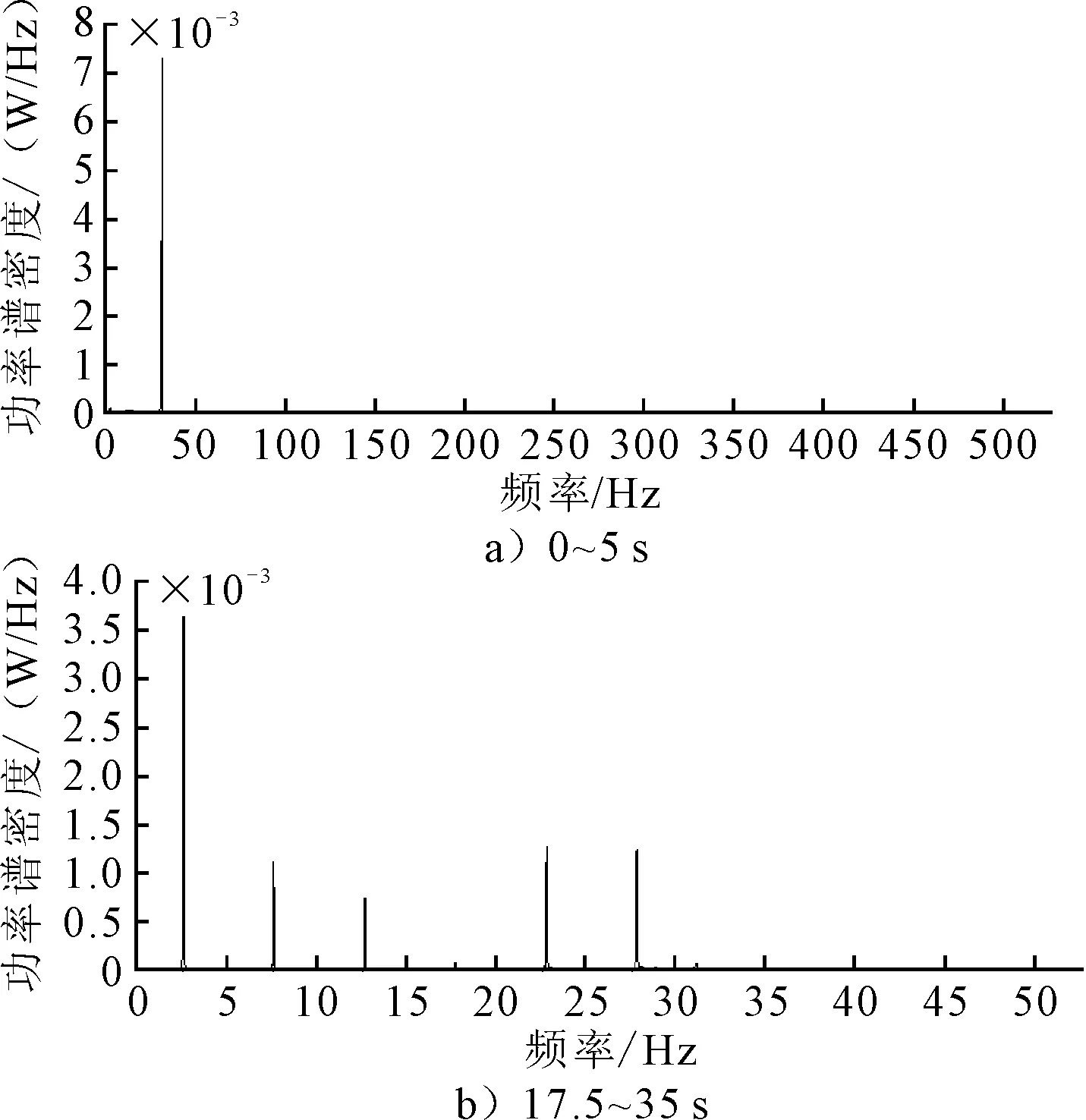
图9 不同时间段升力系数功率谱密度曲线(切角长方形截面A,V=16m/s)

图10 相平面图(切角长方形截面A,V=24 m/s)

由图10可知，相轨迹逐渐扩大，最后稳定在一个极限环内.

4 结 论

1) 运用FLUENT计算吊杆的阻力系数和升力系数随风攻角变化值和风洞实验值基本吻合，通过式(4)计算得到的驰振临界风速两者基本吻合； 通过对FLUENT二次开发，运用流固耦合方法计算得到的驰振临界风速和节段模型风洞实验吹出的驰振临界风速基本吻合.可见这两种数值计算方法具有较高的精度，为今后驰振研究提供了有力工具.

2) 长方形截面切角后，旋涡脱落强度减小，其中切角较大的长方形截面B的涡脱落强度最小.流动形态的改变导致结构受力性能的改变，影响结构的驰振稳定性.

3) 长方形截面切角能否改善驰振性能取决于切角的形状和大小，对切角的形状和大小非常敏感.当顺桥向来风时，长方形截面和切角长方形截面A在较高风速时会发生弛振，表现为随风速增大振幅逐渐增大的极限环振荡.切角长方形截面B在不会发生弛振.为今后工程设计提供了参考.